【光电集成】光栅闪耀波长

众所周知，在某些配置中，衍射光栅可以将入射到其上的大部分能量集中到特定的衍射级。这种现象被称为闪耀。

闪耀和闪耀条件

具有闪耀配置的光栅被称为闪耀条件。重要的是要认识到，正是光栅的特性以及照明条件促成了所谓的闪耀条件。

测量光栅衍射的光强称为效率。闪耀波长被定义为在给定衍射阶数m中效率曲线达到其最大值的波长。图1显示了典型的效率曲线（衍射强度与波长的关系），闪耀波长记为λB。

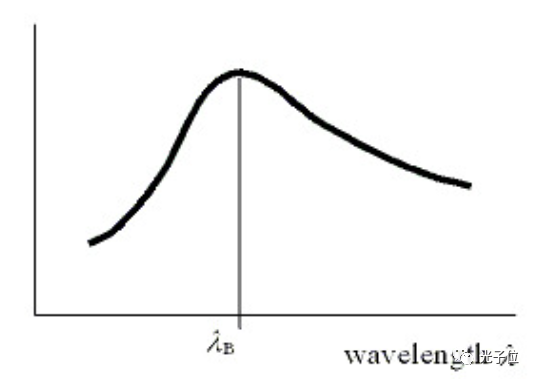
图1 典型的效率曲线：对于给定的衍射级，光栅衍射的光的强度随波长变化。

Littrow配置中的闪耀波长

光栅的凹槽图案对由其衍射的光的方向的影响由光栅方程控制：

mλ = d(sinα + sinβ) (1)

其中，α是入射角，β是衍射角，λ和m是波长和衍射级数，d是光栅表面上相邻凹槽之间的间距。

Littrow配置是从光栅衍射到给定衍射级的特定波长的光沿着入射光的方向往回传播的特定几何形状：在上面的等式（1）中，需要满足：

α = β (Littrow配置 ) (2)

对于Littrow配置，光栅方程可简化为：

mλ = 2dsinα (3)

等式（1）中给出的一般配置和Littrow配置如图2所示：

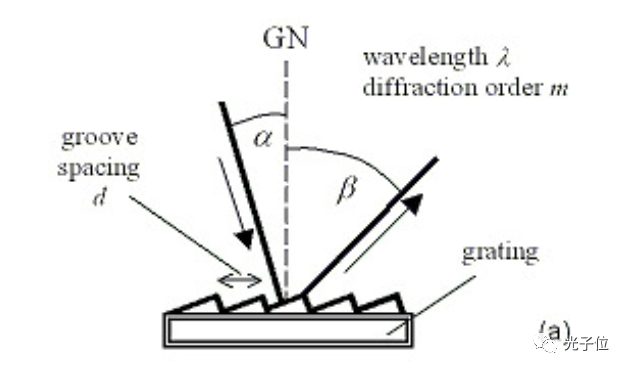
图2a 一般平面内衍射条件。特定波长λ的光以相对于其表面法线GN的角度α入射到光栅上，并且该光沿着相对于表面法线的角度β衍射到特定阶数m。入射光线和衍射光线都位于垂直于凹槽方向的平面内（“平面内衍射”）。

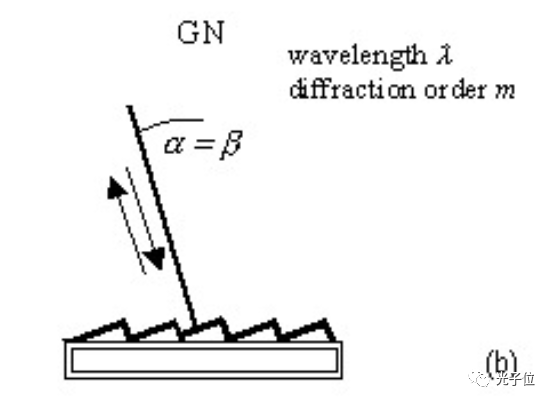
图2b。Littrow配置。在这种情况下，α=β。注意，在每种情况下，角度α和β都是有符号的角度（即，在（a）中，α和β具有相反的代数符号）。

Littrow条件下的闪耀波长是指当光栅在扫描波长时保持在Littrow配置，效率曲线（如图1所示）达到最大值的波长。这需要光栅旋转以扫描波长，通常称为单色器配置。

衍射光栅可指示其每个光栅的Littrow闪耀波长（对于第一衍射级，m＝1）。对于刻线光栅（其凹槽是三角形的），其他阶的闪耀波长可以通过近似找到：

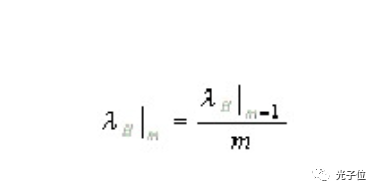
即，m阶的闪耀波长（Littrow配置）近似等于第一阶的闪耀波长除以m。对于全息光栅（其凹槽是正弦的），等式（4）无效。

Littrow闪耀角θB定义为闪耀波长的衍射角（在Littrow条件下）：

mλB = 2dsinθB (5)

其他配置的闪耀波长

当偏离Littrow条件时（即当α≠b时），闪耀波长和闪耀角通常满足条件：

mλB = 2dsinθBcos(α - θB) (6)

也就是说，闪耀波长随着入射角α和Littrow闪耀角θB之间的角度的余弦而减小。根据凹槽轮廓和照明条件，等式（6）可以是非常精确的，或者充其量是近似值。

闪耀波长下的效率

如上所示，虽然确定最大效率的波长λB相对简单，但确定最大效率本身更困难。由于这种计算需要使用麦克斯韦方程组，因此通常通过计算机模拟来解决。有一些基于计算机的光栅效率程序，其中一些可以在商业上获得。

----与智者为伍 为创新赋能----

投稿丨合作丨咨询

联系邮箱：uestcwxd@126.com

QQ：493826566