引言
BUCK-BOOST电路是一种常用的DC/DC变换电路,其输出电压既可低于也可高于输入电压,但输出电压的极性与输入电压相反。下面我们详细讨论理想条件下,BUCK-BOOST 的原理、元器件选择、设计实例以及实际应用中的注意事项。
电路原理
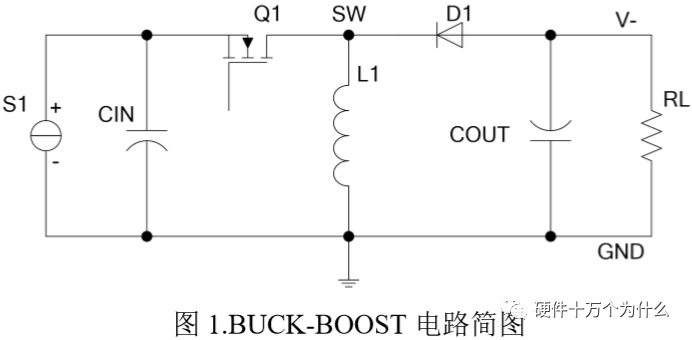
BUCK-BOOST电路简图如图1。
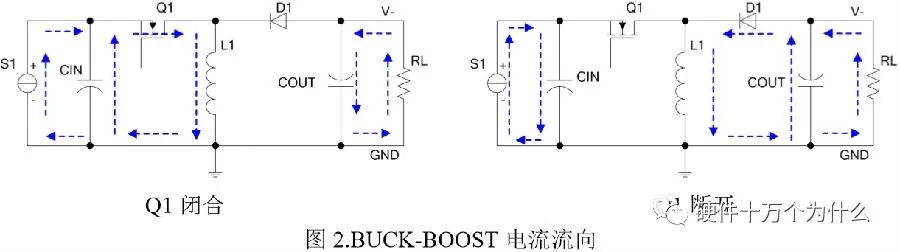
当功率管Q1闭合时,电流的流向见图2左侧图。输入端,电感L1直接接到电源两端,此时电感电流逐渐上升。导通瞬态时di/dt很大,故此过程中主要由输入电容CIN供电。输出端,COUT依靠自身的放电为RL提供能量。当功率管Q1关断时,电流的流向见图2右侧图。输入端VIN给输入电容充电。输出端,由于电感的电流不能突变,电感通过续流管D1给输出电容COUT及负载RL供电。系统稳定工作后,电感伏秒守恒。Q1 导通时,电感电压等于输入端电压VIN;Q1关断时,电感电压等于输出端电压VOUT。设T为周期,TON为导通时间,TOFF为关断时间,D为占空比(D=TON/T),下同。由电感伏秒守恒有:
由此可得:
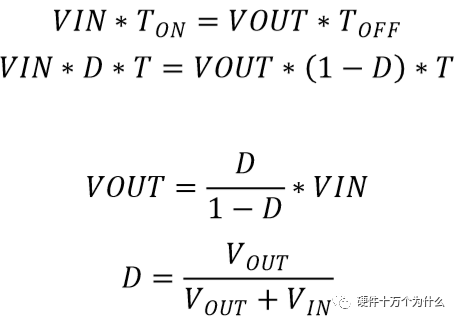
占空比小于0.5时,输出降压;占空比大于0.5时,输出升压。以上式子只考虑电压的绝对值,未考虑输出电压的方向。
元器件计算及各点波形(电感电流连续模式)
以下均在电感电流连续模式下讨论,即CCM。
首先我们先看一下各点理想情况下的波形:
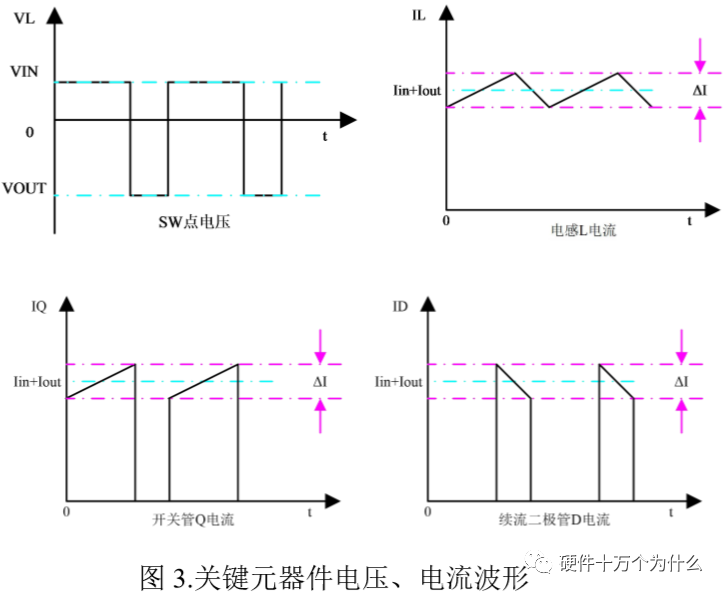
电感 L1
通常ΔI可以取0.3倍的IIN+IOUT,在导通时,电感的电压等于输入电压,电感感量可由下式计算:
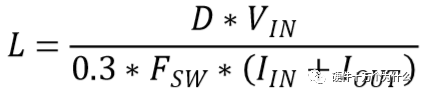
若按上述感量选择电感,则流过电感的峰值电流:
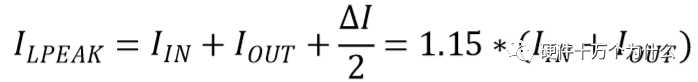
实际应用应留有一定的余量,电感的电流能力通常取1.5*(IIN+IOUT)以上
续流二极管D1
当Q1导通时,续流二极管的阴极SW点电压为VIN,续流二极管的阳极电压为-VOUT,故D1承受的电压为:
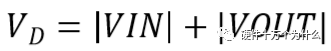
当Q1关断时,续流二极管续流,电流的峰值为ILPEAK,平均电流为IOUT。
由于二极管在高温下漏电容易造成芯片的损坏,故通常要留有一定的余量,其中电压建议1.5倍的余量。
功率管Q1
当Q1关断时,SW点电压被钳位到-VOUT,故功率MOS承受的最大电压:
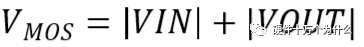
当Q1导通时,Q1的电流峰值为ILPEAK,平均电流为IIN。
输入电容
输入电容纹波电流有效值可用下式计算:
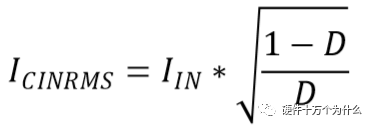
如果设CIN电容在MOS导通时,电压跌落不超过ΔV1,则可用下式计算最小容量:
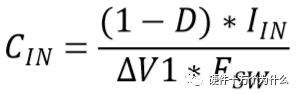
设计实例
要求
输入电压10~14V,输出电压-5V,输出电流1A,选取合适的芯片,并计算主要元器件参数。
解决步骤
1.计算输入电流:输出功率约5W,输入最大电流,假设80%的效率,则输入电流为 5W/0.8/10V=0.625A;:
2.计算输入峰值电流:1.15*(1A+0.625A)=1.87A;
3.计算功率管、续流肖特基管峰值电压:|-5V|+|14V|=29V;
4.选择合适的芯片,可选耐压为40V左右,电流能力大于2A以上的BUCK降压芯片,此处选择XL4201;
5.计算10V时的占空比:D=5V/(5V+10V)=0.33;
6.计算电感量:L=0.33*10V/(0.3*150KHz*(1A+0.625A))=45uH;
7.计算最小电流能力IL=1.5*(1A+0.625A)=2.44A,选用47uh/3 电感;
8.肖特基二极管耐压要大于29V,平均电流1A,峰值电流约1.87A,可选SS36;
9.输入电容纹波电流有效值:ICINRMS=0.625A*sqrt((1-0.33)/0.33)=0.89A,“sqrt”代表根号;
10.假设输入电压最大跌落0.05V,则CIN=(1-0.33)*0.625A/(0.05V*150KHz)=56uF,选用47uF电解电容;
11.输出电容纹波电流有效值:ICOUTRMS=1A*sqrt(0.33/(1-0.33))=0.70A;
12.假设输出放电电压最大跌落0.05V,则COUT=0.33*1A/(0.05V*150KHz)=44uF,选用100uF电解电容。
实际电路可参考下图:

注意事项
1. 芯片与肖特基二极管D1的耐压均要大于输入电压与输出电压绝对值之和;
2. CINB与C1为芯片提供纯净电源,CINB可以选用10uF以上电容即可;
3. 芯片的GND引脚与输入、输出功率地不是同一属性,注意区分;
4. BUCK-BOOST电路的效率要低于单纯的BUCK或BOOST电路,实际使用时要注意多留余量。
在非隔离电源方案中,Buck、Boost、Buck-Boost电路应用非常广,很多工程师对这三种电路非常熟。下面介绍四开关Buck-Boost电路。
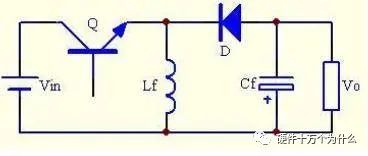
常规的Buck-Boost电路,Vo=-Vin*D/(1-D),输出电压的极性和输入电压相反。
简要的四开关Buck-Boost电路,Vo=Vin*D/(1-D),输出电压的极性与输入电压相同。
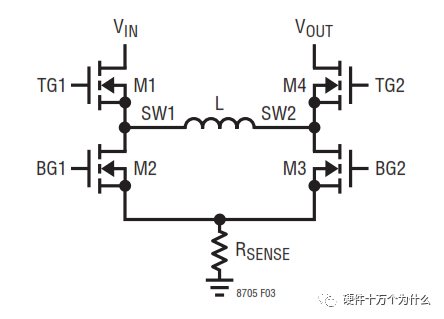
四开关buck-boost的拓扑很简单,如下图。
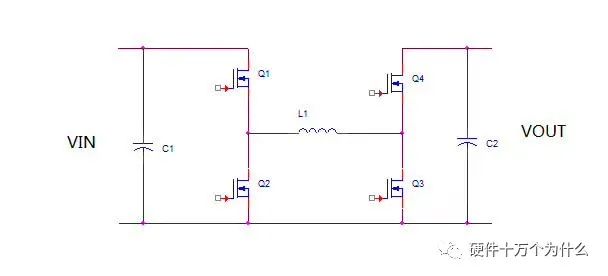
对于四开关buck-boost,它本身有一种非常传统简单的控制方式。
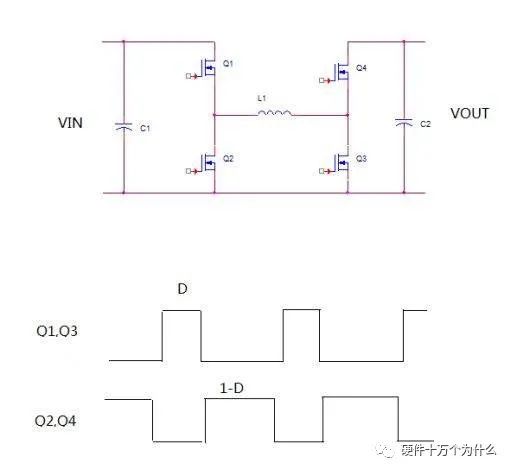
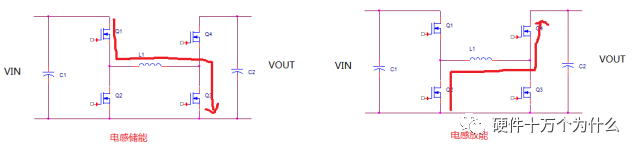
那就是Q1和Q3同时工作,Q2和Q4同时工作。并且两组MOS交替导通,如上图。
如果把Q2和Q4换成二极管,那么也是同样能工作,只不过没有同步整流而已。
对于这种控制方式,在CCM情况下我们可以得到公式:
Vin*D=Vout(1-D)也就是说,Vout=Vin*D/(1-D). 这个电压转换比和我们常见的buck-boost是一样的。
只不过常见的buck-boost的输出电压是负压,而四开关输出的是正压。
但是这种控制方式的优点是简单,没有模态切换。但是缺点是,四个管子都在一直工作,损耗大,共模噪音也大。
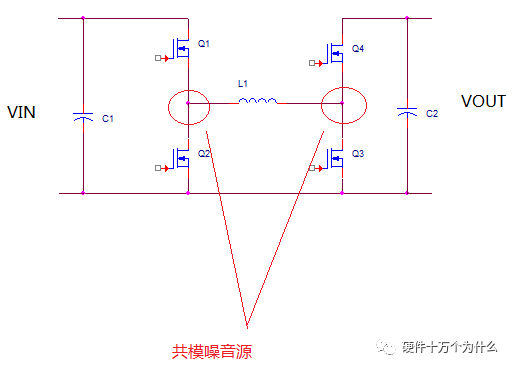
基于传统控制方式的缺点。多年前,一家知名的IC公司推出了一款控制IC,革新了这个拓扑的控制方式。
其思路就是当Vin〉Vout的时候,把这个拓扑当纯粹的BUCK来用,当Vin
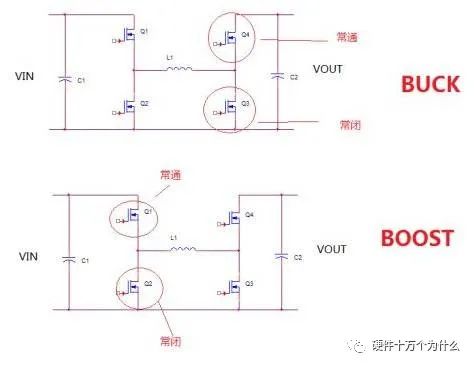
但是,这种思路本身没什么奇特之处。真正有技术含量的是,当VIn=Vout的时候,采用怎么样的控制方式?
从buck过渡到中间模态,再过渡到boost的时候,如何做到无缝切换? 这几个问题,后来成为各家IC公司,大开脑洞,争夺知识产权的战场。
接下来,我来介绍某特公司的IC的控制逻辑。
先假设输出为固定的12V,输入假设为一个电池,充满电电压为16V,放电结束电压为8V。
那么从输入16V开始,此时的工作状态显然是BUCK
那么四个管子的驱动信号如下图
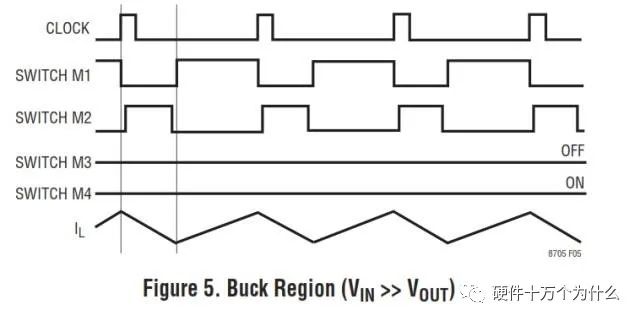
那么当输入电池电压逐渐开始降低,M1的占空比也逐渐开始增大,而M2的占空比开始减小。
此时M2的占空比是个关键的参数。
因为IC内部对M2的脉宽有个最小设定,假如说是200ns。
那么现在假设输入电压掉到12.5V,而M2的脉宽也收缩到了200ns。IC内部的逻辑电路就认为到了模态切换的时候了。
此时发生的变化是,M3和M4两个管子不再是常关和常通的状态,而是开始开关了。
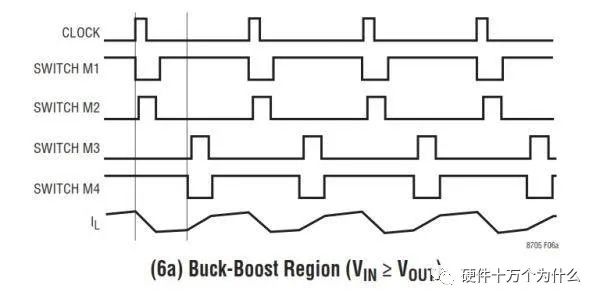
如果我们把上图进行分解,就会发现一个有趣的现象,就是在一个clock周期里面,前半周期是buck,后半周期是boost
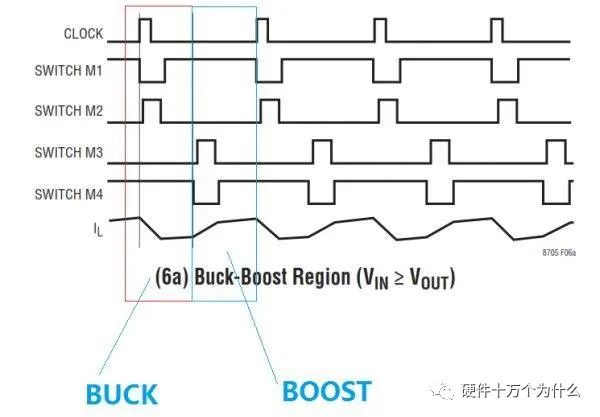
这个时候boost切进去的时候,M3是以最小占空比切入的,而且该占空比不可调。
此时M2的占空比则会从最小突然展宽以抵消boost模特切入的影响。在这个时候,输出会产生一个动态效应。
那么当输入继续下降的时候,M2的占空比会继续减小。
那么当M2再度回到最小占空比的时候,IC内部逻辑电路会认为模态需要再次转换了。
此时,M2将固定在最小占空比,而M3则开始跳出最小占空比,可以逐渐展宽。理论上来说,这个过渡应该是完全无缝的切换,
但是由于芯片内部的clock时序的切换,也会对输出造成一种动态效应。
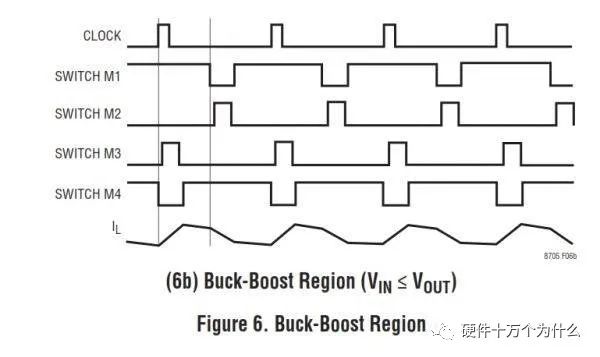
这个时候,变成了前半周期是boost,后半周期是buck。
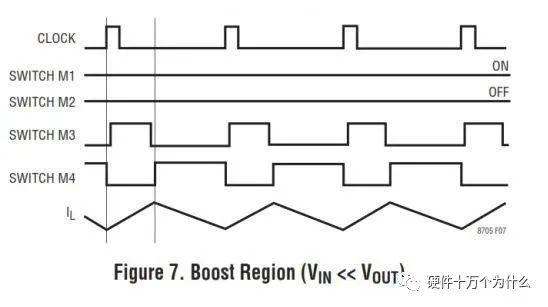
同样,当输入电压继续降低的时候,电路会切入完全的boost模态。
本文整理自:
《BUCK-BOOST 拓扑电路浅析》深圳劲锐佳科技有限公司
《深度解读四开关Buck-Boost电路及变换器》电子发烧友电子圈
《BUCK BOOST BUCK-BOOST电路的原理》百度文库
近期热文:
后台回复“加群”,管理员拉你加入同行技术交流群。
你若喜欢,点个“赞”和“在看”