【半导光电】激光器中光与物质的基本相互作用

今日光电

光在激光器中是经过以下过程产生的：物质中的电子从激发态能级跃迁到较低能级，发射光子，贡献于激光
束的产生。因此，光与物质之间的基本相互作用是分析激光器运行和激光特性的基础。这一节简略描述激光 材料中的原子/ 分子与生成激光的光子之间的相互作用。

能级

原子能级由原子中的电子与原子核及其他电子的相互作用决定。电子从一个能级移动或者跃迁到另一个能级， 会吸收或者发射一定能量。这是光子与物质中的原子相互作用的主要机制。这些能级及其相应的光子能量取决于 原子的电子结构。图3 所示为原子的通用能级图。分子是由两个或者更多原子组成的，它们的能级由原子间作 用力决定。除电子跃迁之外，分子还具有与振动和旋转能级相关的跃迁，这导致了比简单原子更为复杂的能级集 合（见图3）。如一大群相同的原子/ 分子彼此分离，比如在稀薄气体中，每个原子/ 分子具有相同的离散能级集 合。然而，当原子/ 分子彼此接近，比如在液体或者固体中，各种分子间的相互作用变得愈加重要，最初的离散 的原子或分子能级逐渐扩大成大量密集的能级的集合，形成能带[1]。绝缘体和半导体的价带和导带及其能带间隙 如图3 所示。

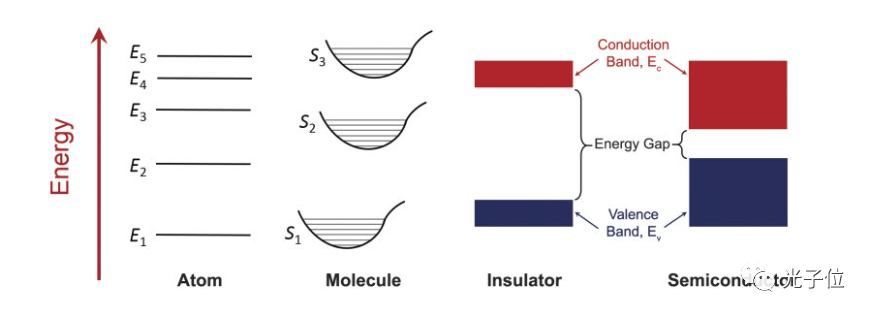
Figure 1: Energy：能量；Atom：原子；Molecule：分子；Insulator：绝缘体；Semiconductor：半导体；Conduction Band：导带；Energy Gap：能隙；Valence Band：价带；图3 原子间相互作用增强时的能级演化图示（从左至右）：孤立原子，孤立分子，固体绝缘体，固体半导体。

辐射过程

忽略组成材料的物质类型，光与原子的相互作用有三个基本过程，实现能级间的向上和向下跃迁。图
4 所示为称为自发辐射的过程，当一个原子处于上能级（E 2）或者激发态，可自发地衰变到较低能级（E 1），同时 辐射出一个光子。由于每种材料都有一组特定的能级系统，发出的光子会拥有该材料特定的能量。光子的能量与 光的频率（ν ）和波长（λ ）有如下关系：

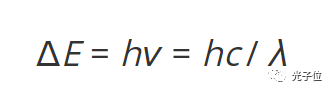
其中h 是普朗克常量， c 是光速。图4 所示的第二个过程是吸收过程。当原子最初位于较低能级时，可吸收一个 特定能量hν 的光子，将其激发至较高能级。图4 中最后一个过程是受激辐射。受激辐射本质上是吸收的逆过程， 也需要存在一个能量为hν 的光子，但原子最初处于上能级。光子激发原子，使其辐射一个与最初原始光子具有相 同特性的复制光子，包括光子能量、传播方向、相位和偏振态。受激辐射以 牺牲储存在原子中的能量为代价产生光子，导致光放大或者光增益。这一现象对于激光器的运转至关重要。

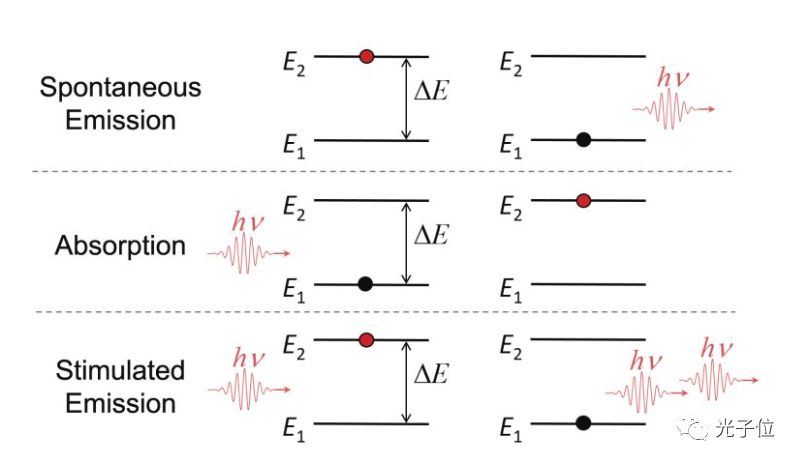
Figure 2: Spontaneous Emission- 自发辐射；Absorption- 吸收；Stimulated Emission- 受激辐射
图4 当光子(hν) 与组成物质的原子发生相互作用时能够发生的三个辐射过程：相互作用之前（左）和之后（右）的系统。

跃迁截面

一个有助于定量描述原子- 辐射相互作用的术语是跃迁截面σ (ν ) 。该数值描述了可能发生的相互作用的
强度或者概率，并且适用于上述三个辐射过程。如图5 所示，跃迁截面取决于光子的频率或者波长。它是以共振 频率(ν 0) 为中心，此时σ (ν ) 为最大值。随着ν 偏离ν 0，跃迁截面逐渐减小。有几个关键的量：峰值跃迁截面，σ 0 = σ (ν 0)；线宽(Δν )，代表最大值下降到一半时所对应的频率范围（半高宽）；以及线下面积(S )，称作跃迁强度 或者振荡强度。跃迁截面常用跃迁强度和分布曲线来描述：

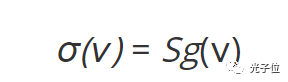
其中线型函数g (ν ) 是具有单位积分面积的归一化函数。这种描述可以把总的跃迁强度从它对频率的依赖性中独立 出来。许多过程会构成g (ν ) 的展宽，用线宽Δν 描述，包括均匀展宽和非均匀展宽；由于方程（2）适用于受激辐射，它在激光放大/ 增益过程中的重要性是不言而喻的。大的跃迁强度会产生 较大的激光增益系数，同时分布曲线有助于确定频率响应和增益带宽。

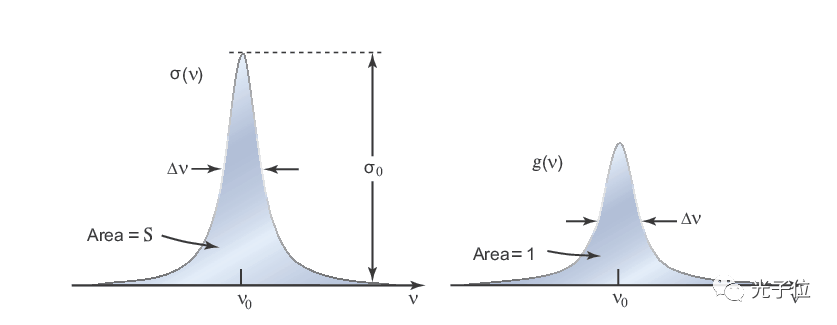
Figure 3: Area- 面积 图5 跃迁截面σ(ν)（左）和线型函数g(ν)（右）[1]

粒子数反转

辐射过程的描述（图4）说明它们的影响与处在各个能级上的原子数量相关。对于处在热平衡状态的系统，
原子位于特定能级的概率服从玻尔兹曼分布。如图6 所示，随着能级增加，这个概率呈指数下降。如果只考虑E 2 和E 1 两个能级（如图6 所示），那么玻尔兹曼分布给出了两个能级的粒子数N 2 和N 1 的比值：

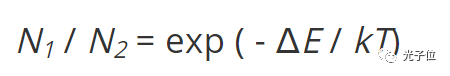
其中k 是玻尔兹曼常数，T 是温度。对于激光跃迁，典型的能级差(ΔE ) 比室温下的kT 高出两个数量级，因此N 2/ N 1 << 1。由于大多数粒子处于最低能级，吸收过程占主导地位，这是光与大多数物质相互作用的典型方式。此外， 少量粒子处于上能级，受激辐射的可能性很低。然而，如果有一定数量的粒子数被转移到较高能级，使得N 2 超过 N 1，就可以实现非平衡条件，即粒子数反转。粒子数反转是激光作用的先决条件，因为受激辐 射是实现放大的途径。

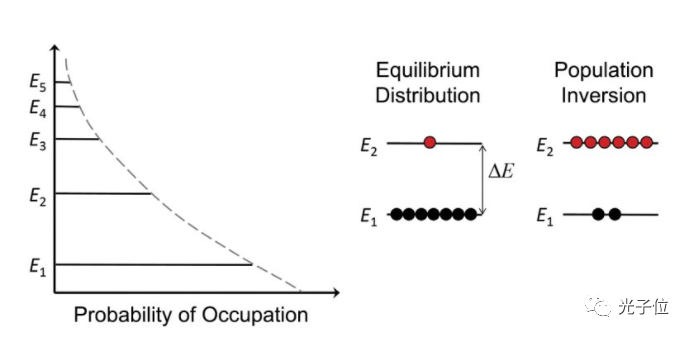
Figure 4: Probability of Occupation- 占有概率；Equilibrium Distribution- 平衡分布；Population Inversion - 粒子数反转 图6 原子占据处于热平衡的原子能级的概率（左，[1]）。平衡条件下的粒子数分布和粒子数反转（右）。

----与智者为伍 为创新赋能----

投稿丨合作丨咨询

联系邮箱：uestcwxd@126.com

QQ：493826566