
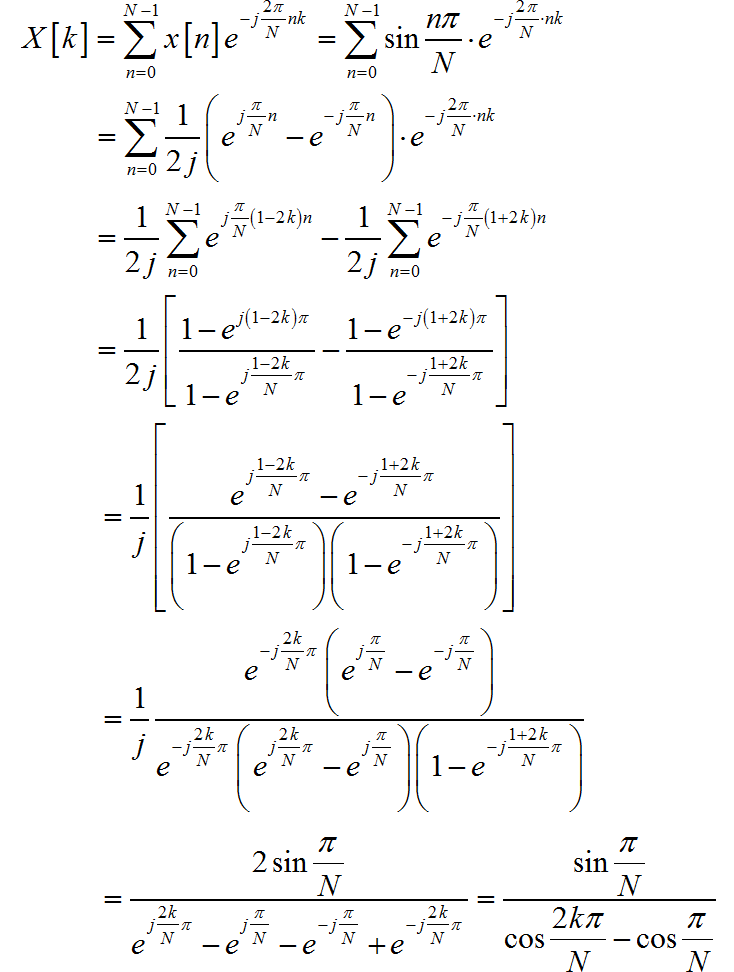
(1) 数据采集时间间隔等于数据采集频率 的倒数。根据要求, 信号中最高频率 , 那么 。因此数据采集间隔 :
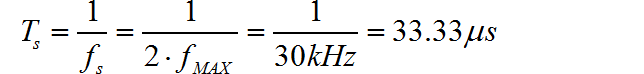
(2) 根据频率分辨率 , 因此要求数据采样总时间:
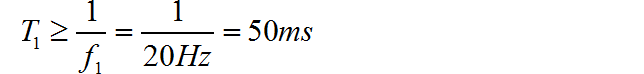
那么采样数据点
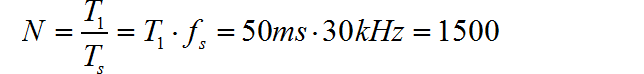
为了适应 FFT 算法, 最终取 。
根据题目条件, 可以知道 是对 进行 点的DFT。所以对应的反变换 是对 进行 的周期延拓后, 再取主值区间, 即:
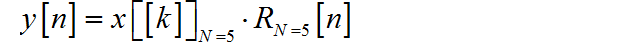
(1) 根据 , 它周期延拓之后形成如下的周期序列。
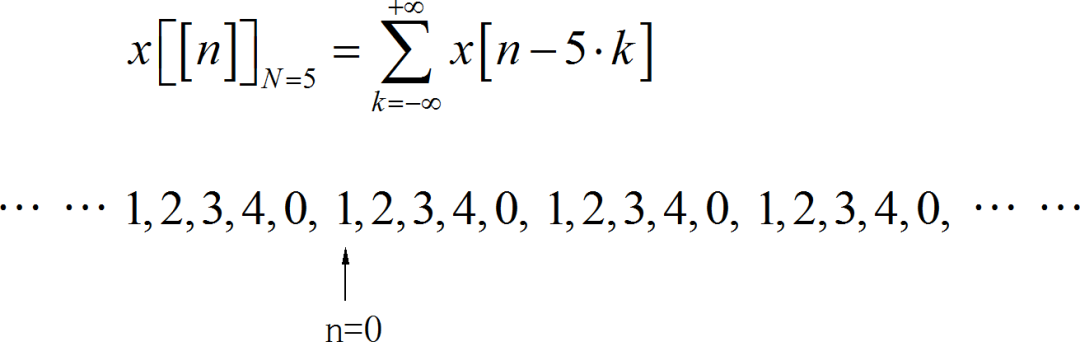 那么
那么
(2) 根据 , 它的周期延拓之后形成如下周期序列:
 那么
那么
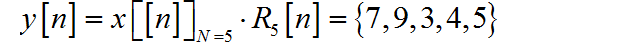
(1) 直接使用(线)卷积计算 ,所需要的的实数乘法为
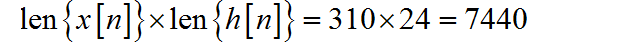
所需要的实数加法为
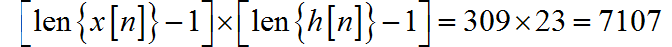
为了说明上述结论, 可以有列表法求解序列卷积过程, 展示了所有惩罚和加法册数。
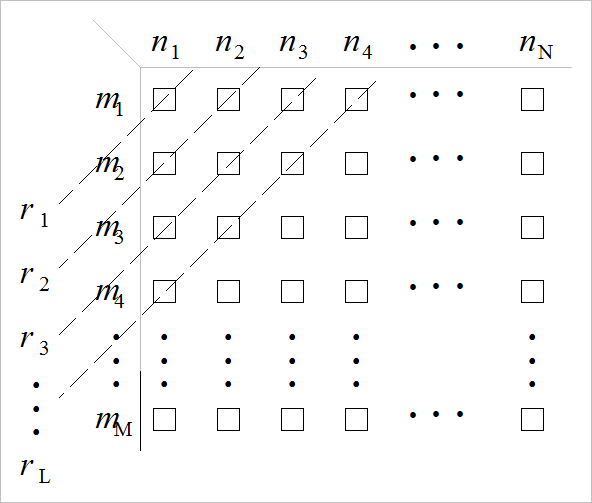
▲ 图1.1.1 表格法计算离散序列卷积示意图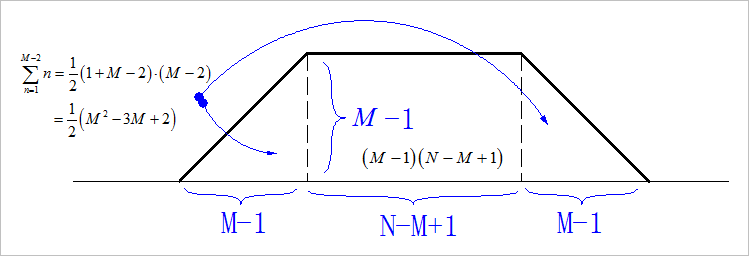
▲ 图1.1.2 . 以M(2) 利用 基-2 的 FFT, 完成 之间的线卷积。根据课件上给定的快速计算框架, 其中所需要的计算过程包括:
计算过程需要三次 FFT 的计算复杂度 和一次变换域内的成绩, 因此:
* **复数乘法次数** :
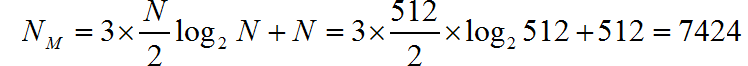 * 复数加法次数:
* 复数加法次数:

根据附属的运算,最终所需要的实数乘法次数和加法次数为:
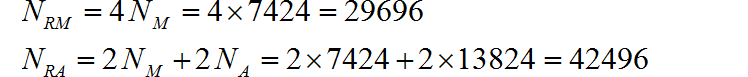
(3) 对比上面频谱分析中的计算结果, 可以看到使用 FFT 计算所需要的计算量远比直接计算卷积所需要的计算量还要大!因此, 利用FFT实现快速卷积所使用的序列需要满足一下两个条件:
对于长度 的序列 , 应用 DFT 计算所需要的复数乘法和加法为:
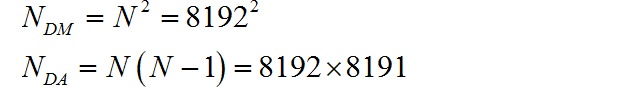
所需要的实数乘法和加法次数:
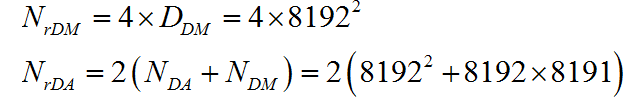
单片机所需要的计算时间:
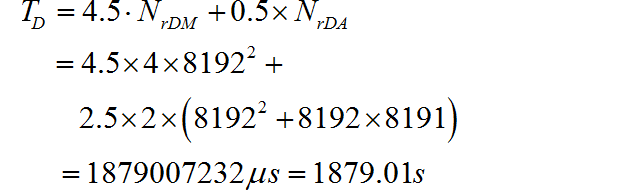
使用 FFT 所需要的复数乘法和加法的次数为:
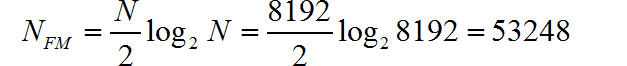
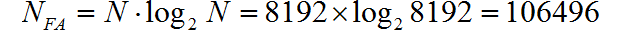
所需要的实数乘法和加法的次数:
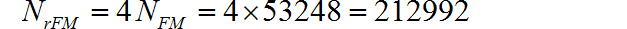
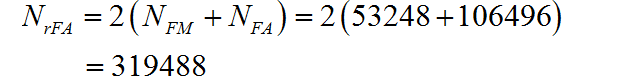
因此 单片机所需要的运算时间为:
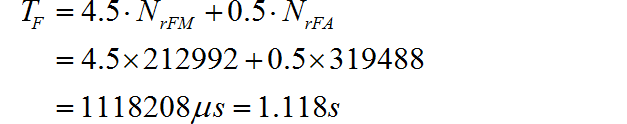
对比 直接使用 DFT 和 FFT 单片机的运算时间, 使用 FFT运算速度提高了大约 1680 倍。
答案是 D。根据匹配滤波器的特点, 要求发送信号的自相关的能量约集中越好, 使得时间延迟检测更加精确。下面是四个心慌可波形:

▲ 图1.2.1 四个信号的波形上面四个信号的自相关波形为:
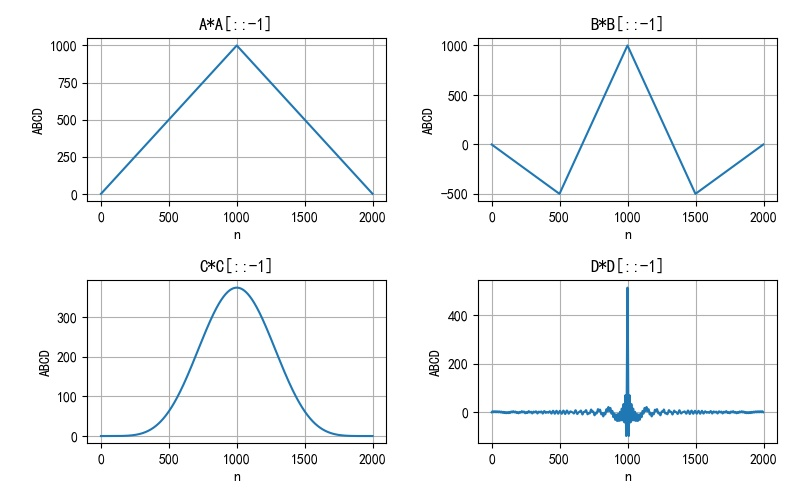
▲ 图1.2.2 四个信号的自相关波形(1) 根据佩里-维纳准则, 要求 积分有限。
对于 进行积分, 根据 的原函数:
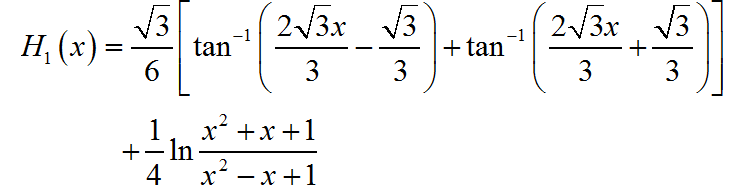
所以
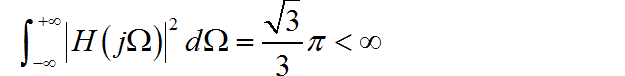
所以该系统是物理可实现的。
(2) 由于
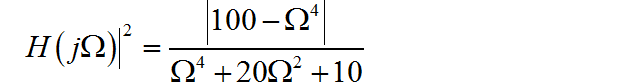 当 趋于 取值部位 0, 所以它的积分是发散的。根据佩里-维纳准则, 这个系统不满足绝对可积,所以该滤波器无法物理实现。
当 趋于 取值部位 0, 所以它的积分是发散的。根据佩里-维纳准则, 这个系统不满足绝对可积,所以该滤波器无法物理实现。
(1)
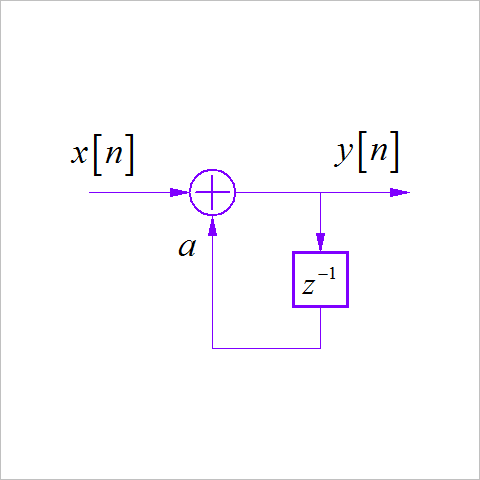
(2)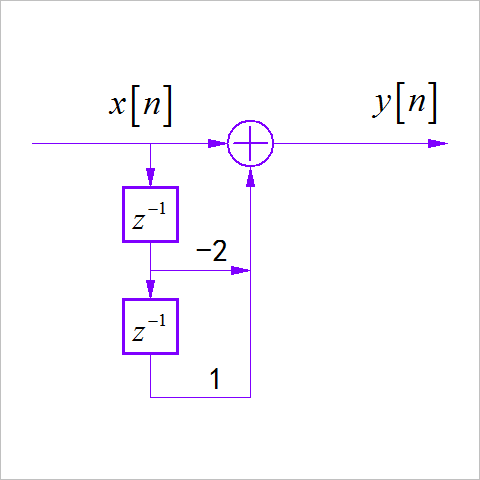
(3)
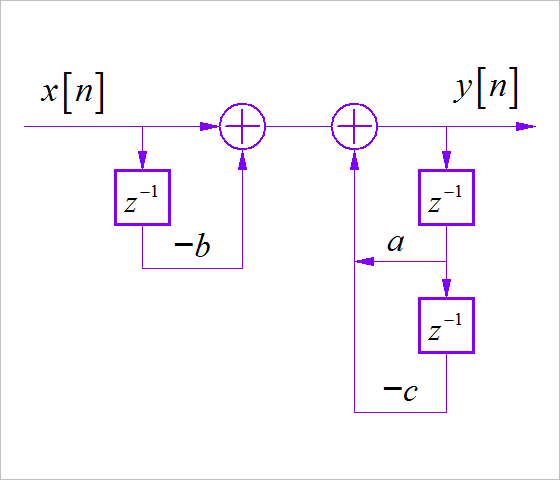
(4)
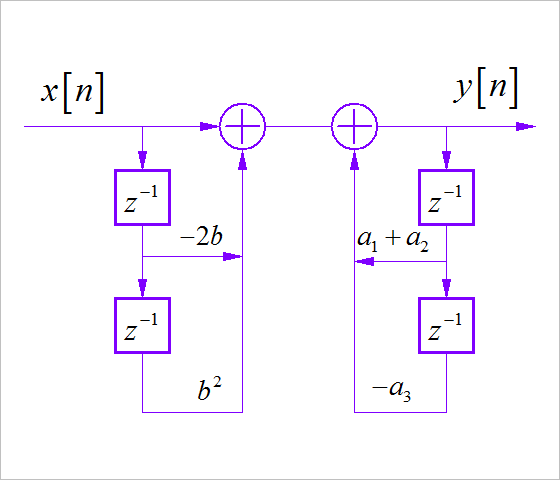
(5)
(1)

对应的数字滤波器为
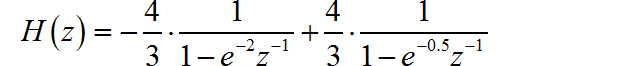
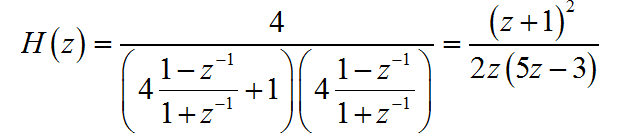
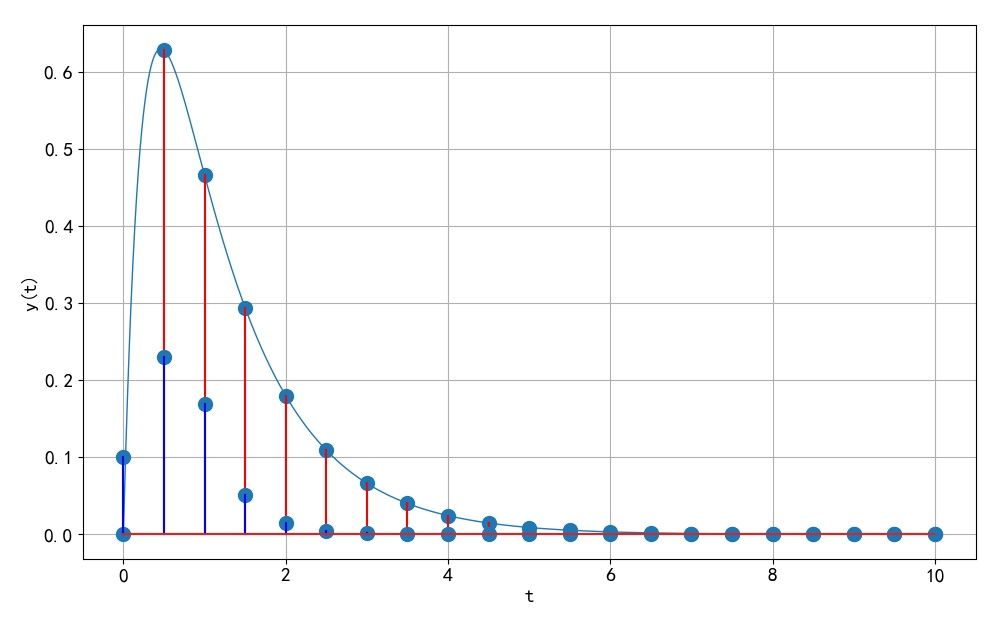
▲ 单位冲激响应不变方法和双线性方法对应的单位冲激响应(2)

对应数字滤波器的系统函数为:
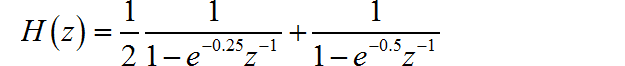
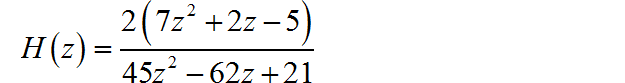
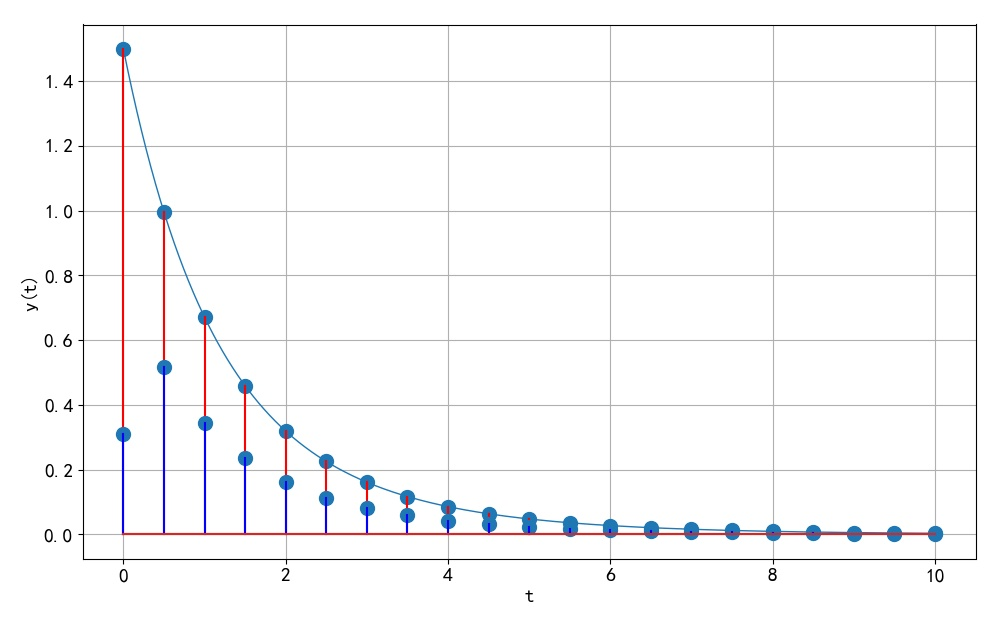
▲ 图1.2.3 冲激响应不变方法与双线性方法对应的单位冲激响应信号信号与系统 2023(春季) 作业要求 - 第十四次作业: https://blog.csdn.net/zhuoqingjoking97298/article/details/130975334
[2]信号与系统 2023年春季作业要求与参考答案汇总: https://blog.csdn.net/zhuoqingjoking97298/article/details/130018064?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22130018064%22%2C%22source%22%3A%22zhuoqingjoking97298%22%7D
