点击蓝字 关注我们
点击文末的“赞”和“在看”，并发送截图和您的邮箱地址到后台，即可领取原版文档哦~
本文介绍了使用图 12 中的电路图作为参考的设计程序，其中谐振电感是用漏感实现的。设计规格如下所示：
标称输入电压：396 VDC（PFC 级输出）
输出：24 V/12 A (288 W)
保持时间的要求：20 ms
PFC 输出的直流链路电容：330 μF
作为第一步，请定义以下规格信息。
估计效率 (Eff)：估算功率转换效率，以计算给定最大输出功率下的最大输入功率。根据估计效率，最大输入功率为：
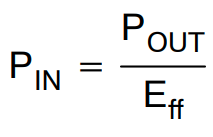（公式11）
输入−电压范围：最大输入电压将是标称 PFC 输出电压。
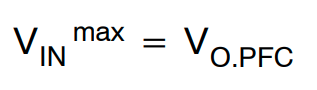（公式12）
尽管 PFC 预调节器会调节输入电压，但它在保持时间内也会下降。所需保持时间内的最小输入电压为：
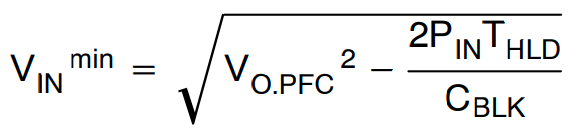（公式13）
其中 VO.PFC 是标称 PFC 输出电压，THLD 是保持时间，而 CBLK 则是直流链路大容量电容。
假设效率为 96%，
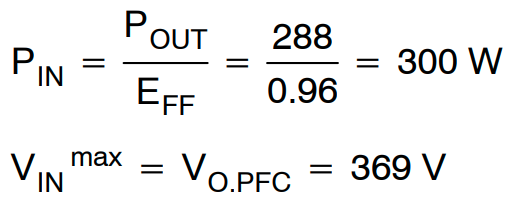
对于 20 ms 的保持时间，可以得到最小输入电压为
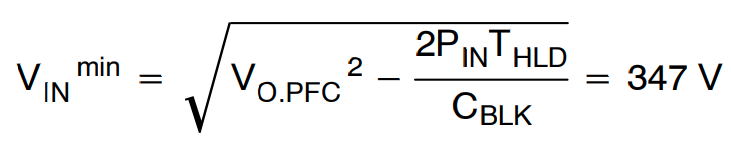
为了获得更大的裕量，最小输入电压设置为 300V。
一旦确定了 LLC 谐振转换器的最小和最大输入电压，我们就可以确定 LLC 转换器的最小增益和最大增益。
标称输入电压需要最小增益。为了最大程度减小开关频率变化，通常是让 LLC 谐振转换器在谐振频率附近工作。谐振频率下的电压增益为：
（公式14）
在保持时间期间，PFC 输出电压（LLC 谐振转换器的输入电压）下降，因此需要更高的增益来调节输出电压。最大电压增益为：
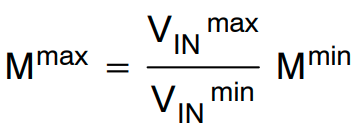（公式15）
我们可以用一个较小的 m值来获得更高的峰值增益；然而，如果 m值太小，就会导致变压器耦合不佳和效率降低。通常是将 m 值太小设置在 3~7 左右。
Lp 和 Lr 之间的比率 (m) 选择 5.69。最小增益由下式获得：
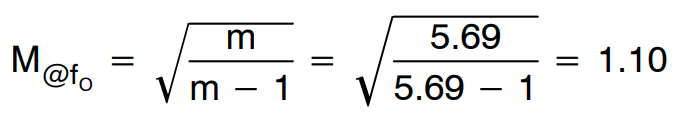
最大输入电压下的最小增益选择 1.13。然后，可以得到最小输入电压的最大增益为
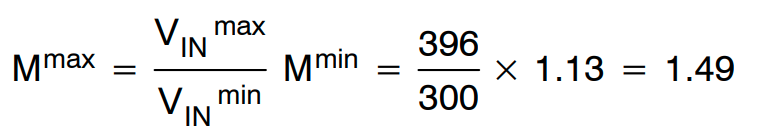
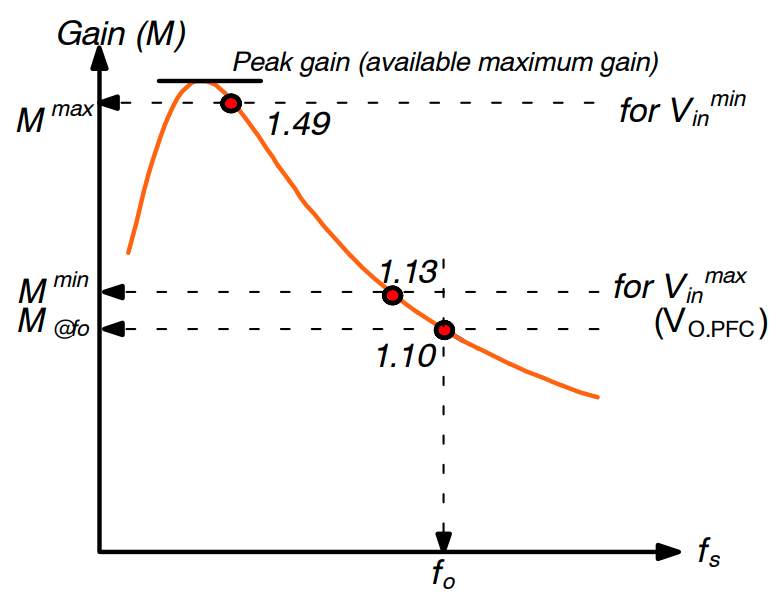
图 13：最大增益/最小增益
利用步骤−2 中获得的最小增益 (Mmin)，我们可以计算变压器匝数比如下：
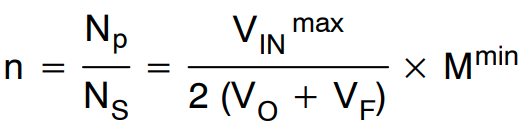（公式16）
其中 VF 是次级侧整流二极管压降。
由于 SR 用于输出整流器，对于具有低 RDS.ON 的 SR MOSFET，VF假设为 0V。由此，可以得到变压器匝数比为
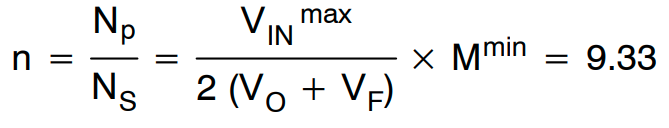
利用从公式 (16) 获得的变压器匝数比，我们可以计算等效负载电阻。
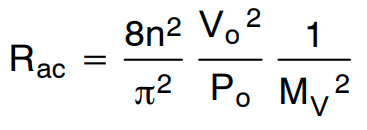（公式17）
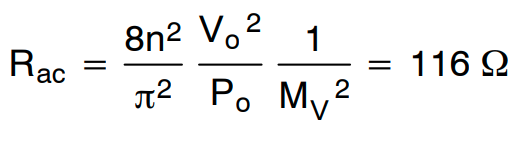
在步骤−2 中选择 m 值后，从图 10 中的峰值增益曲线中读取适当的 Q 值，以获得所需的最大增益。由于峰值增益曲线是使用基波近似生成的，因此谐振下的实际增益要比使用基波近似的预测值高约 10~15%。
一旦确定了 Q 值，我们可以获得如下谐振分量：
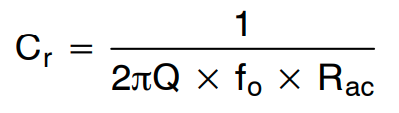（公式18）
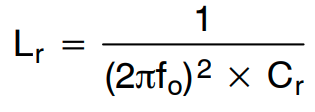（公式19）
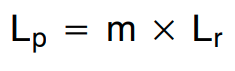（公式20）
按照步骤−2 中的计算，Mmax为 1.49。在步骤−2 中，m 值选择 5.69。从图 14 中的峰值增益曲线中，可以得到最大 Q 值为 0.37。
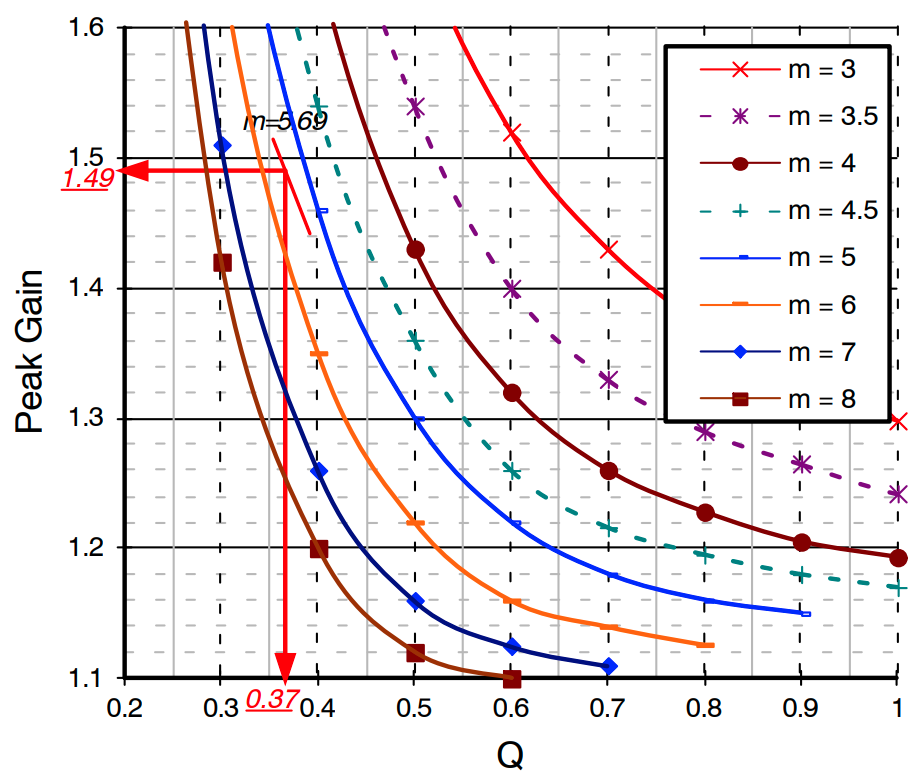
图 14：使用峰值增益（最大可达增益）的谐振网络设计
通过将谐振频率选择为 95kHz，谐振分量确定如下：
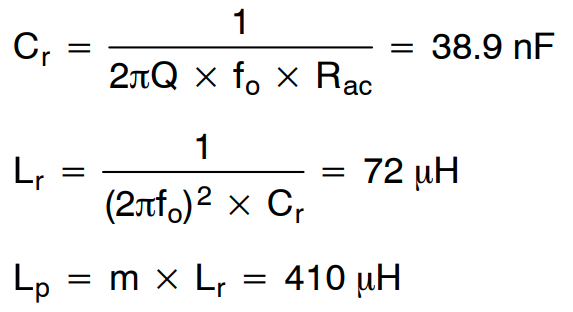
构建变压器时，实际参数将调整如下，以适应 Cr = 48 nF、Lr = 58 H、Lp = 330 H 且 fo = 95 kHz 条件下的标准分量值。
采用基波近似的最终谐振网络设计的增益曲线如下。
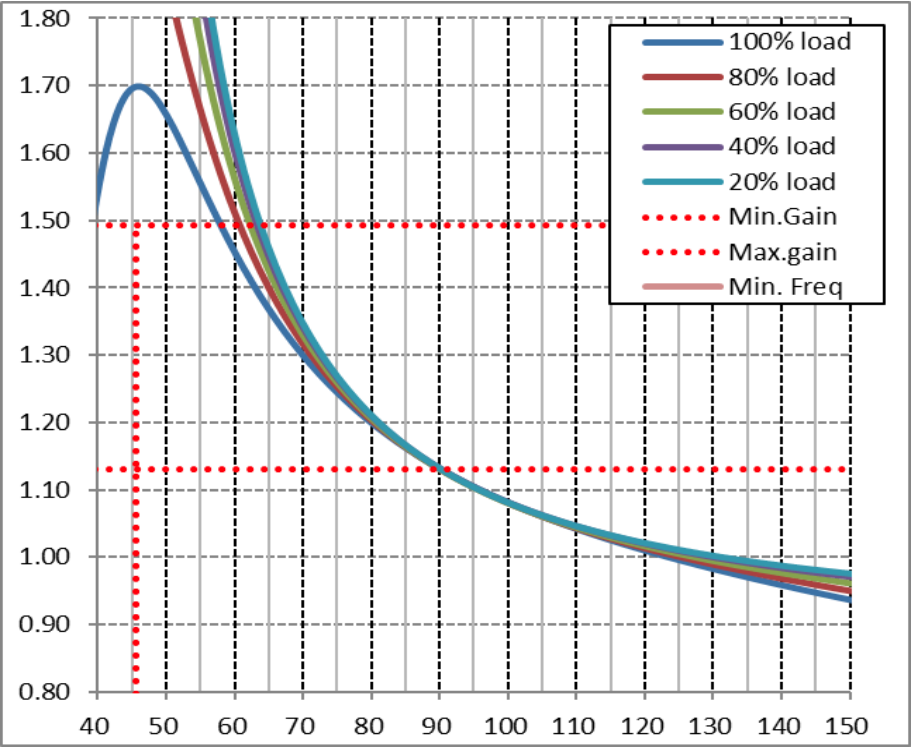
图 15：设计示例的增益曲线
由于在低于谐振工作时，基波近似生成的峰值增益要比实际峰值增益低 10~15%，因此我们进行了 SIMPLIS 仿真以查看实际增益。仿真结果表明，在 75kHz 下，300V 输入可获得所需的最大增益。仿真结果还表明，在标称输入电压和满载条件下的开关频率为 105kHz。
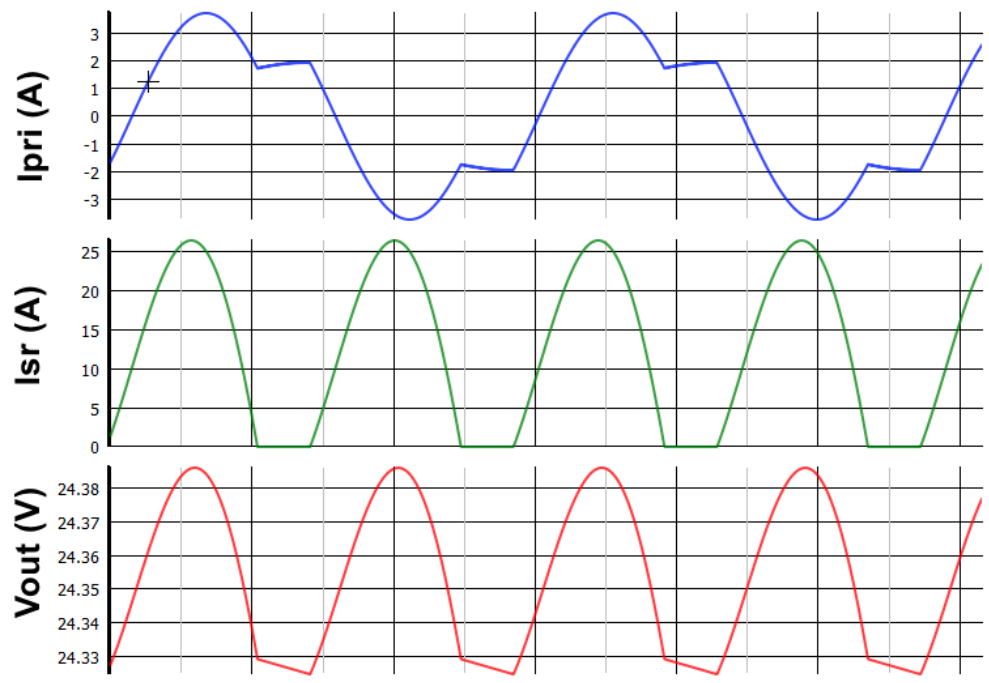
图 16：Vin = 300 V、fs = 69.55 kHz、Po = 288 W 条件下的仿真
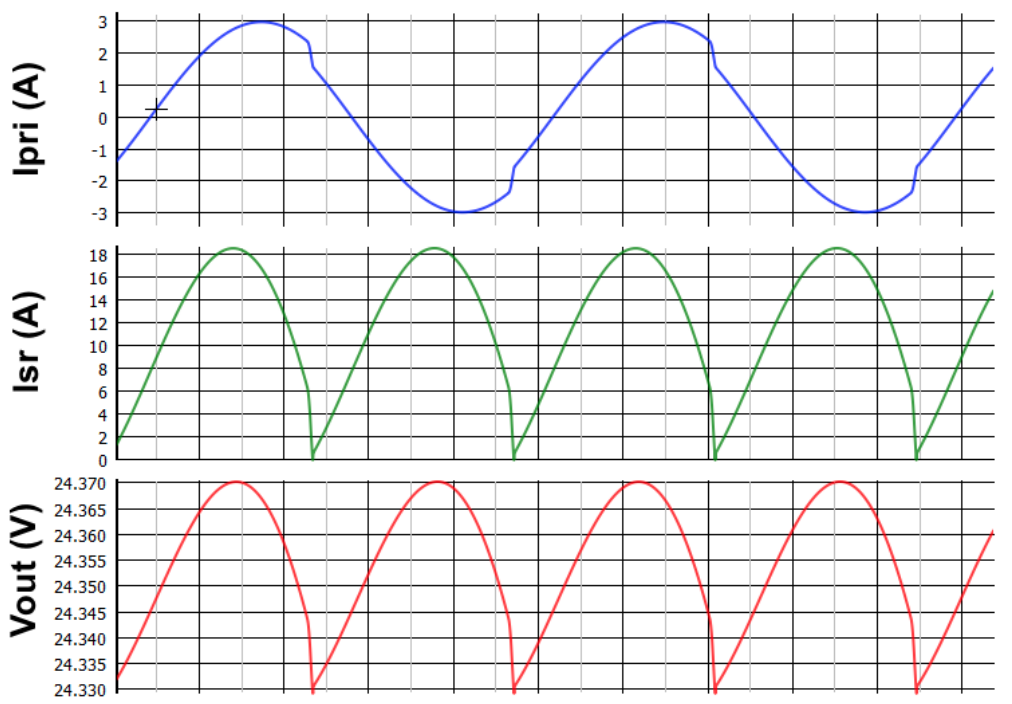
图 17：Vin = 396 V、fs = 105 kHz、Po = 288 W 条件下的仿真
图 18 显示了 LLC 谐振转换器中变压器的励磁电流。初级侧绕组为限制最大磁通密度 Bmax 所需的最小匝数由下式获得：
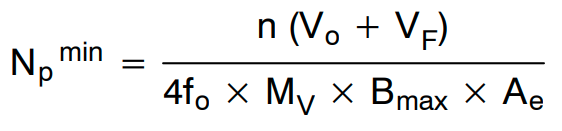（公式21）
其中 Ae 是变压器磁芯的横截面积（单位为 m2），而 Bmax是最大磁通密度摆幅（单位为特斯拉），如图 18 所示。如果没有参考数据，则使用 Bmax= 0.2~0.3 T 来降低磁芯损耗。请注意，公式中出现了由次级侧漏感引起的虚拟增益 MV,（参见图 7）。
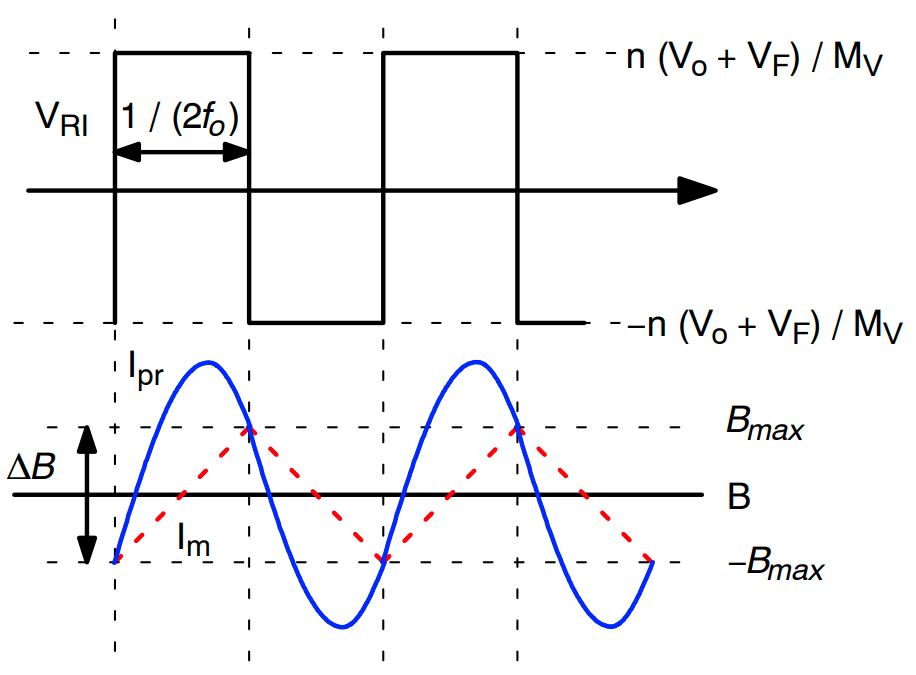
图 18：磁通密度摆幅
为次级侧选择适当的匝数，从而使初级侧匝数高于 Npmin。
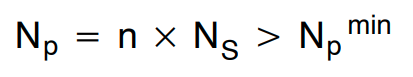（公式22）
初级侧和次级侧绕组的线规应根据标称输入电压下的 RMS 电流确定，由下式给出
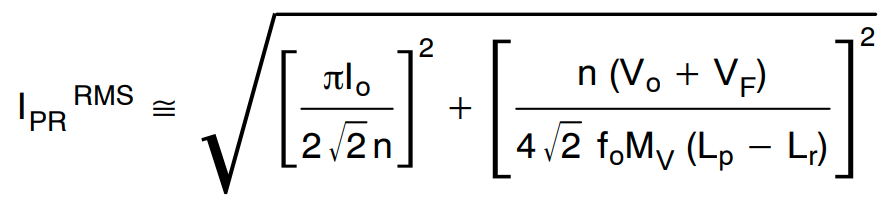（公式23）
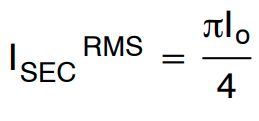（每个绕组）（公式24）
变压器选用 SRV5018 磁芯 (Ae = 189.2 mm2)。Bmax选择 0.1T，以减少变压器的磁芯损耗。变压器的最小初级侧匝数为
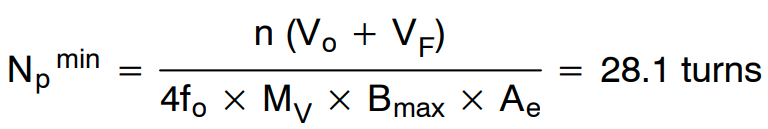
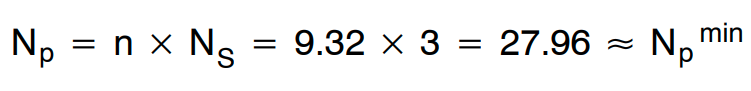
Ns选择 3；Np 选择 28。
标称输入电压下，可以得到变压器绕组的 RMS 电流为
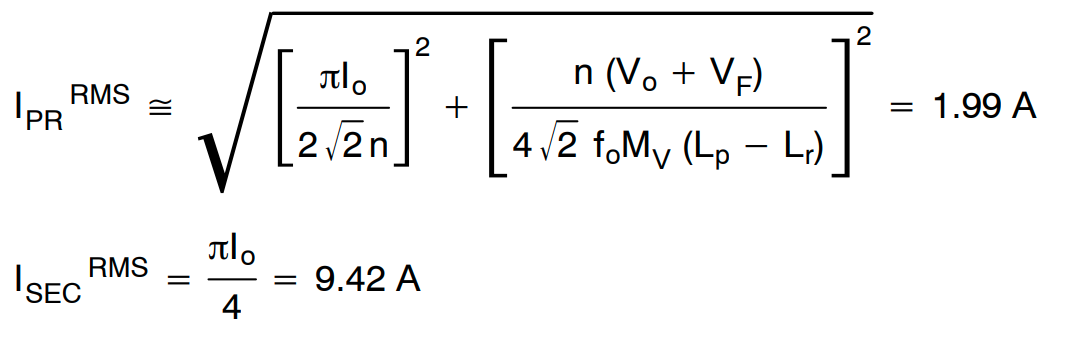
图 19 显示了不同工作条件下的初级侧电流（谐振电容电流）波形。在选择谐振电容时，应考虑到额定电流，因为会有大量电流流过电容器。在标称输入电压下通过谐振电容的 RMS 电流已在公式 (23) 中获得。
标称输入电压和标称负载条件下的最大谐振电容电压由下式给出：
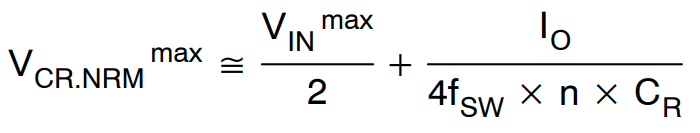（公式25）
谐振电容的额定电压应根据每个角条件下的最大电压确定。
标称输入电压和输出过流条件下的最大谐振电容电压由下式给出：
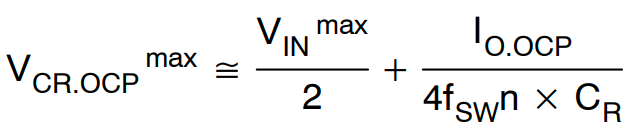（公式26）
最小输入电压和标称负载条件下的最大谐振电容电压由下式给出：
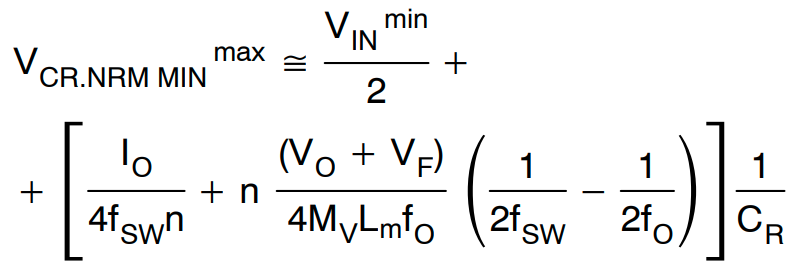（公式27）
请注意，对于全桥 LLC 的情况，应删除公式 (25) − (27) 中的 VIN / 2 项。
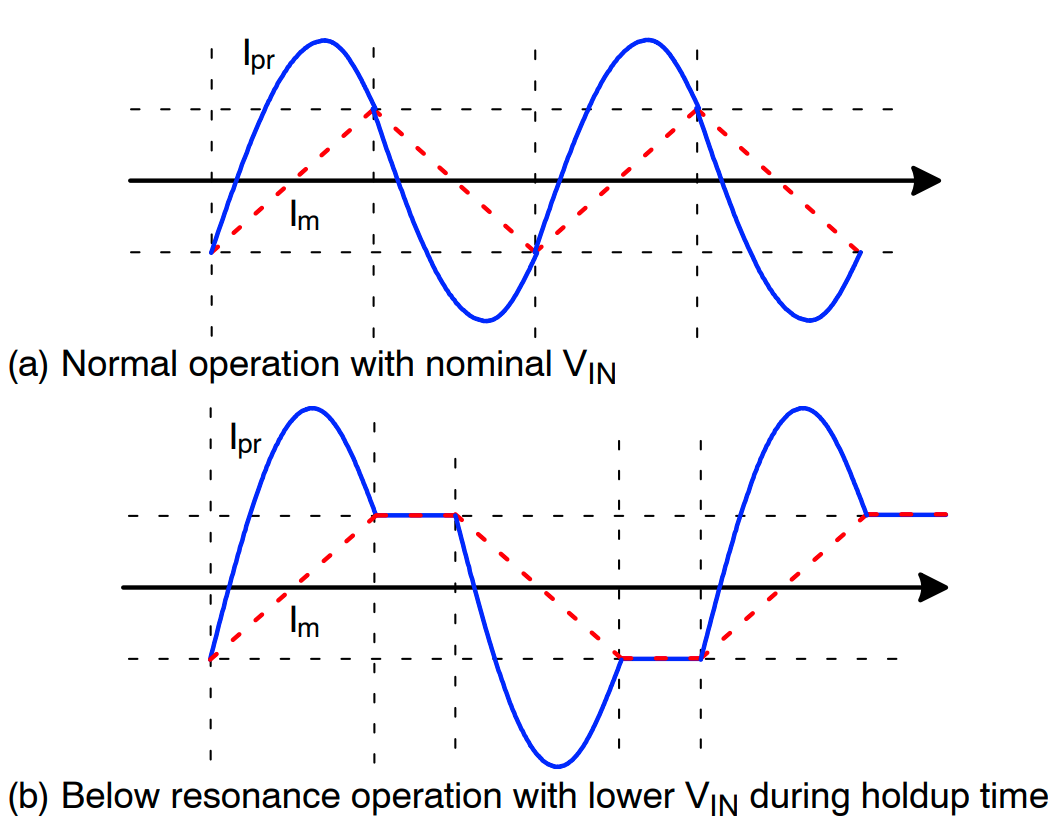
图 19：LLC 谐振转换器在不同工作模式下的初级侧电流波形
在步骤−6 中，谐振电容的 RMS 电流计算如下：
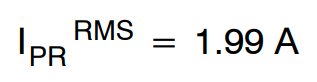
标称输入电压和标称负载条件下的最大谐振电容电压由下式获得：
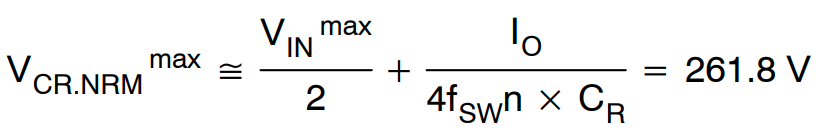
通过将 OCP 电平设置为 13A，可以得到标称输入电压和输出过流条件下的最大谐振电容电压为
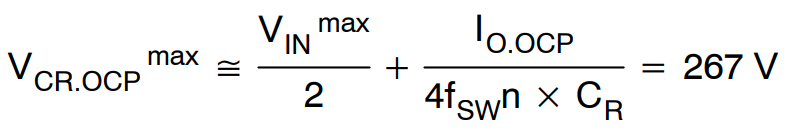
通过将最小频率设置为 65 kHz，可以得到最小输入电压和标称负载条件下的最大谐振电容电压为
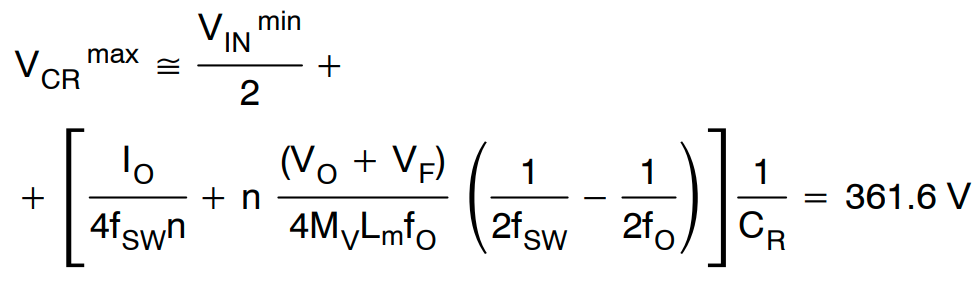
当变压器次级侧使用中心抽头绕组时，二极管电压应力是输出电压的两倍。
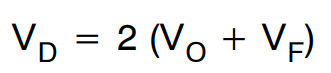（公式28）
流过每个整流二极管的电流的 RMS 值由下式给出：
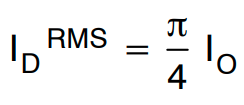（公式29）
同时，流过输出电容的纹波电流由下式给出：
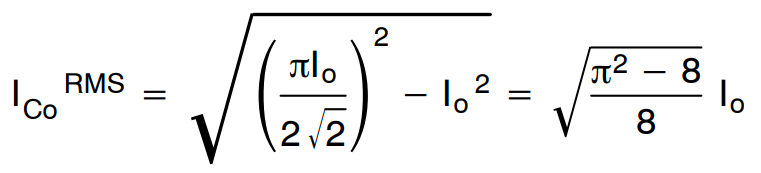（公式30）
输出电容上的电压纹波为
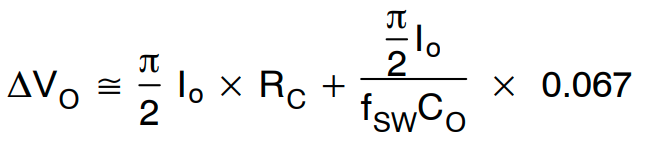（公式31）
整流二极管的电压应力和电流应力为：
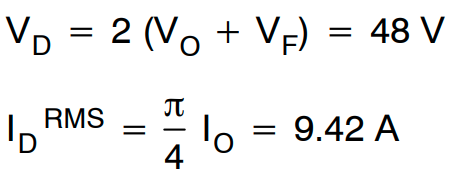
考虑到杂散电感引起的电压过冲，选择 75 V−4.5 mΩ POWERTRENCH® MOSFET 作为同步整流器。每个 MOSFET 上的传导损耗为 0.47W。
输出电容的 RMS 电流为：
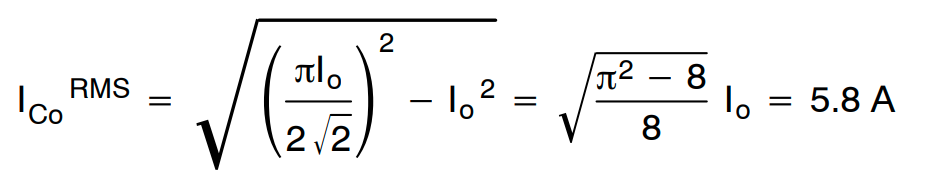
输出电容并联使用四个 1200 μF 电容。每个电容的额定电流和 ESR 分别为 2.77 ARMS 和 15 mΩ。
输出电容纹波计算如下
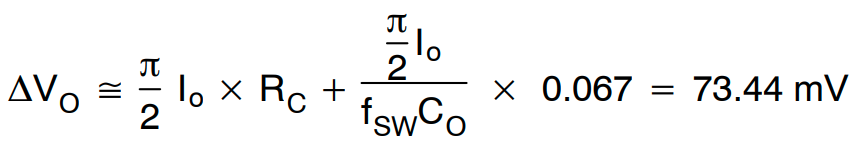
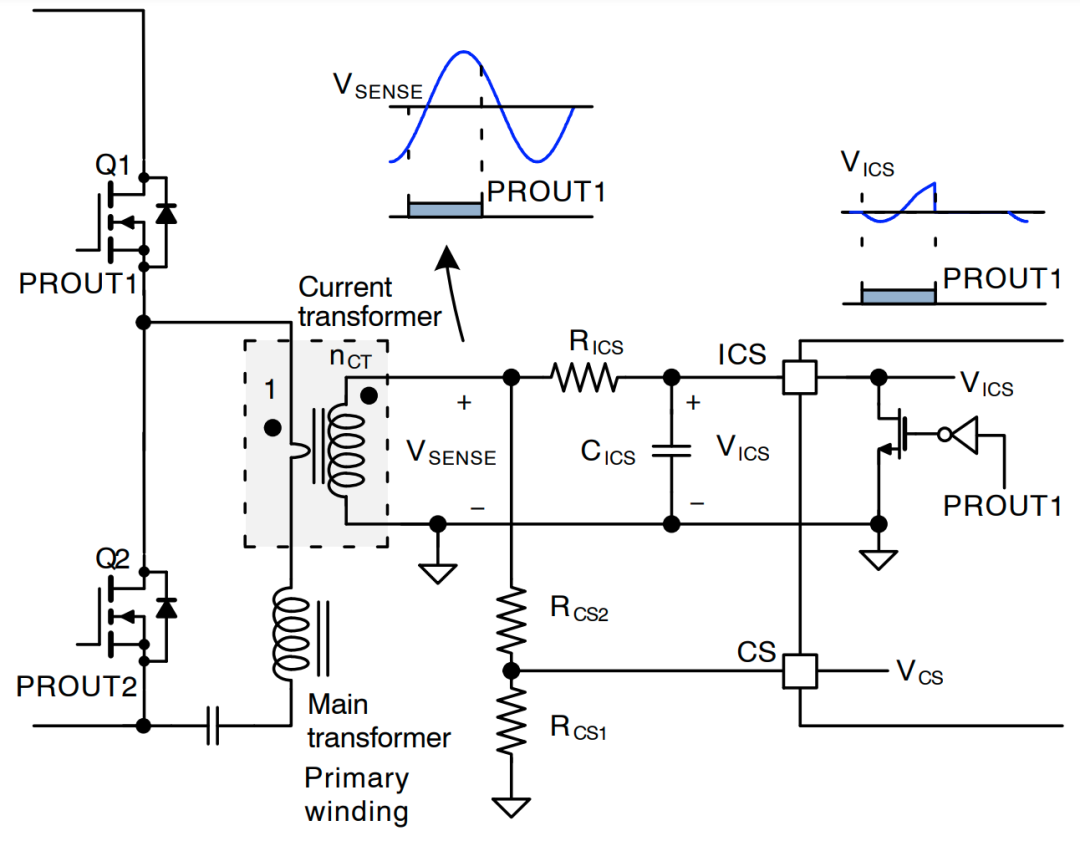
图 20：典型电流检测配置
NCP4390 将检测瞬时开关电流和开关电流的积分，如图 20 所示。由于 NCP4390 位于次级侧，因此要使用电流互感器检测初级侧电流。当 PROUT1 为低电平时，内部复位开关会将 ICS−引脚电压箝位在 0 V。反之，当 PROUT1 为高电平时，ICS 引脚未箝位，积分电容 (CICS) 由流经 RICS 电阻器的电流进行充电和放电。
NCP4390 的应用电路使用 RC 滤波器进行准积分。为了获得准确的积分，电流检测电阻器和电流互感器匝数比的设计应确保 VSENSE 的振幅在大多数时间都高于 VICS。图 23 显示了准积分电路的误差在 PROUT1 (VCM) 的下降沿如何随 VICS 峰值电压与 VSENSE之间的比率而变化。比率越小，积分就越精确。
当 VICS 峰值电压与 VCM之间的比率小于 0.5 时，可获得具有可接受误差（约 10%）的准积分。由于正常工作时 VICS 峰值电压低于 1.2V，因此我们应选择 RCS1 和 RCS2，从而使 VCM 高于 2.4V。
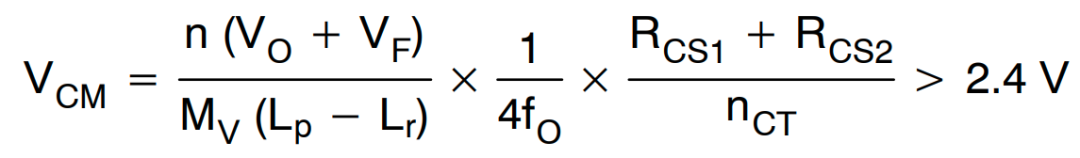（公式32）
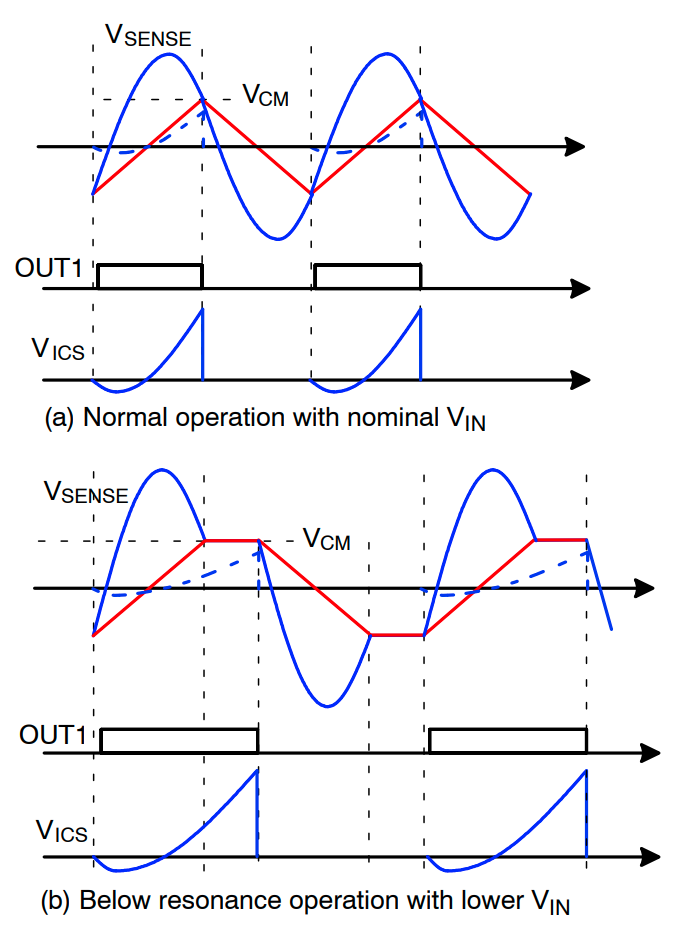
图 21：ICS 引脚波形
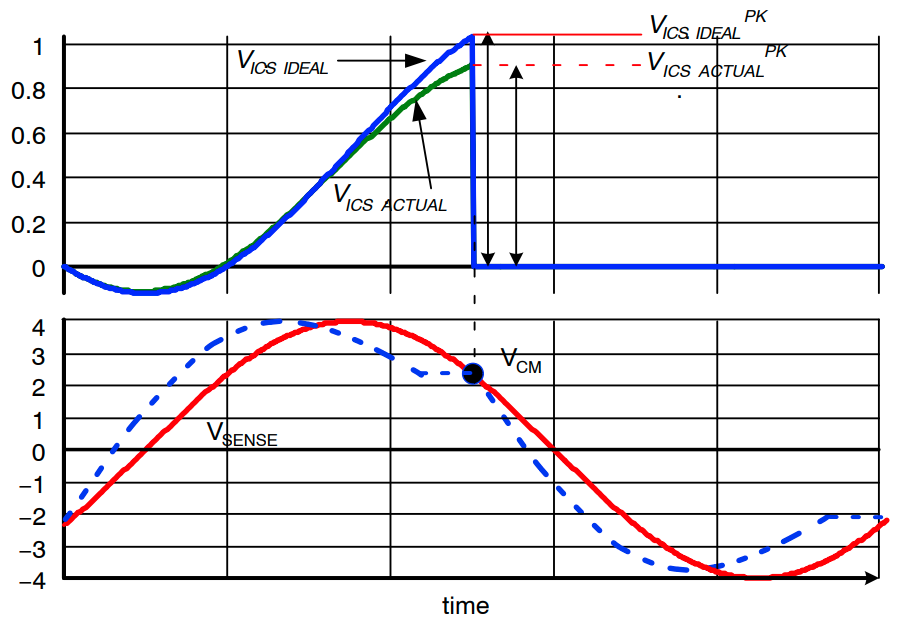
图 22：VICS.IDEALPK 和 VICS.ACTUALPK 的定义
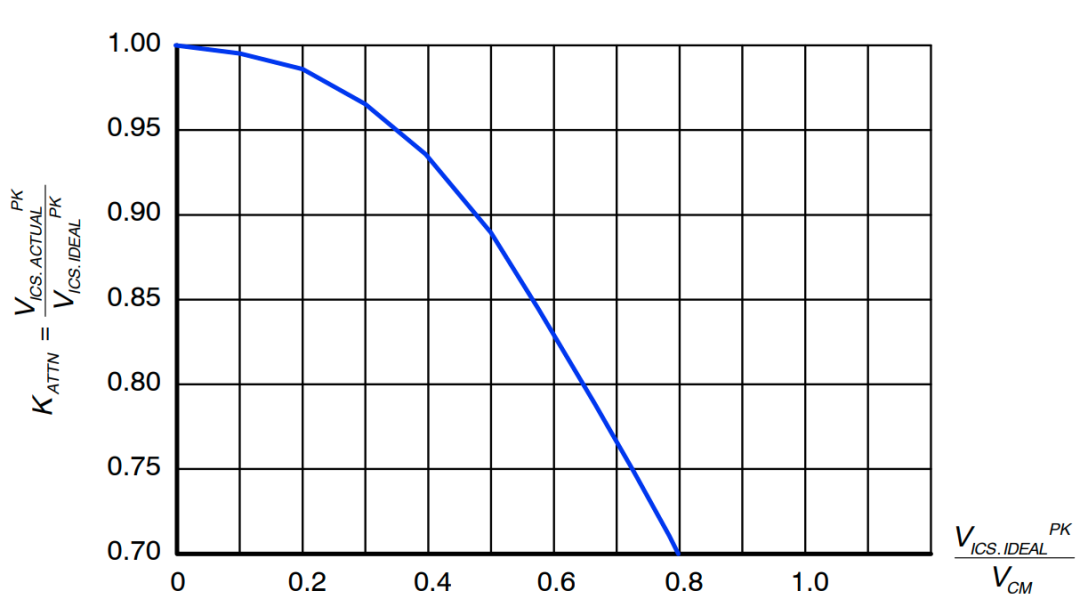
图 23：ICS 引脚电压衰减与 VICS.IDEALPK/VCM
为了获得 VICS 的峰值电压，让我们看一看 LLC 转换器的理想输入功率。对于半桥 LLC 拓扑结构，在将 PROUT1 导通时间定义为 t=0 的情况下，输入功率可由下式表示：
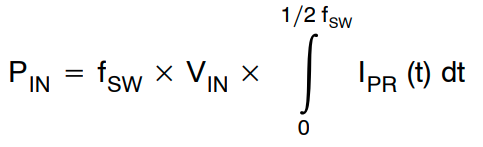（公式33）
请注意，对于全桥 LLC 的情况，等号的右侧应乘以 2。
假设积分理想，ICS 的峰值电压可由下式表示：
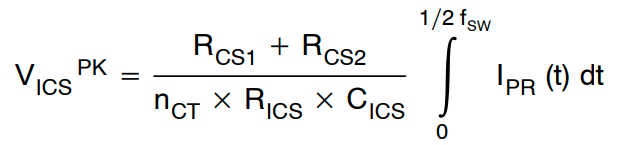（公式34）
结合 (33) 和 (34)，ICS 峰值电压可由下式估算：
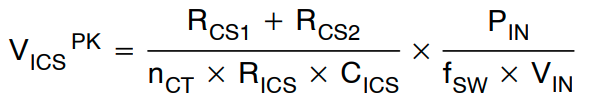（公式35）
考虑到 ICS 引脚内部放电开关的能力，CICS 的典型值为 1 nF。为了精确积分，我们建议使用 1% 容差的电容。
当 VICS 峰值电压与 VCM 之间的比率不够小时，请将图 23 中的衰减系数应用于公式 (35)。
电流检测电压 (VICS) 积分的峰值与开关周期中 LLC 谐振转换器的平均输入电流成正比，如图 24 所示。因此，根据对应于输入电流限值阈值的额定功率的百分比，SR 启用/禁用的负载条件被确定为满载条件的百分比。通常，120% 的额定负载条件用于过流跳闸点，SR 分别在 15% 和 7.5% 的额定负载下启用和禁用。如果过流跳闸点的额定负载条件为 140%，SR 将在额定负载的 17.5% 和 8.75% 时启用和禁用。
为了在不增加 SR 启用/禁用点的情况下获得更高的过流限制，可以通过 ICS 和 5VB 引脚之间的电阻器 RSLP 在 VICS上施加额外的斜率。这项技术通常用于较长保持时间的情况。对于给定的 RSLP，为 ICS 引脚电压额外施加的斜率由下式给出：
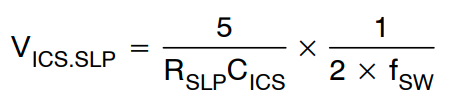
（公式36）
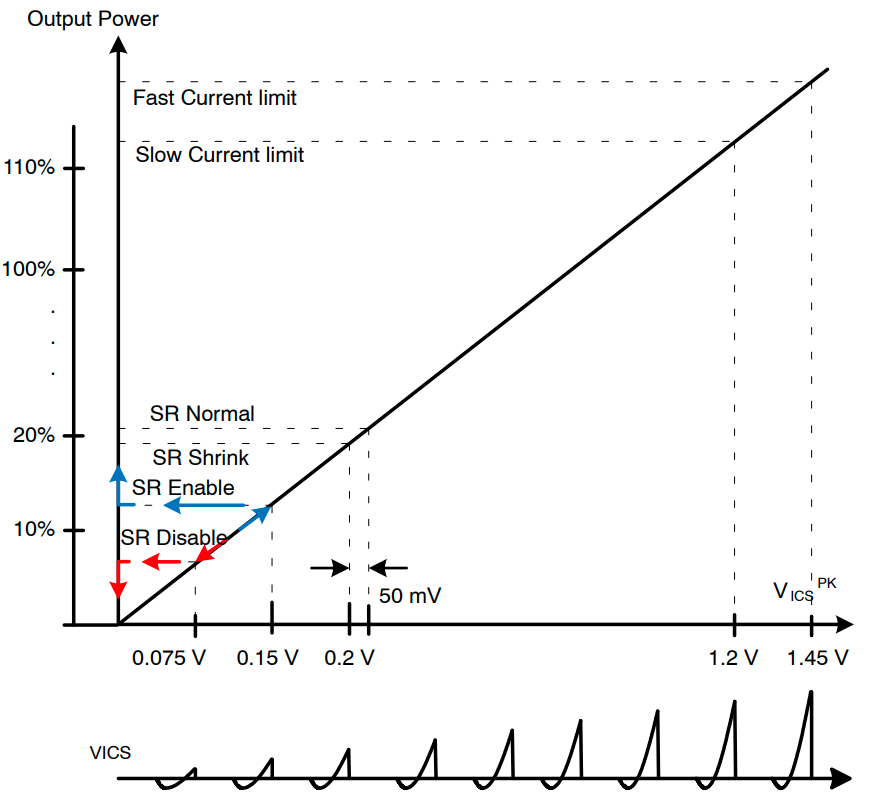
图 24：负载条件和 ICS 引脚电压
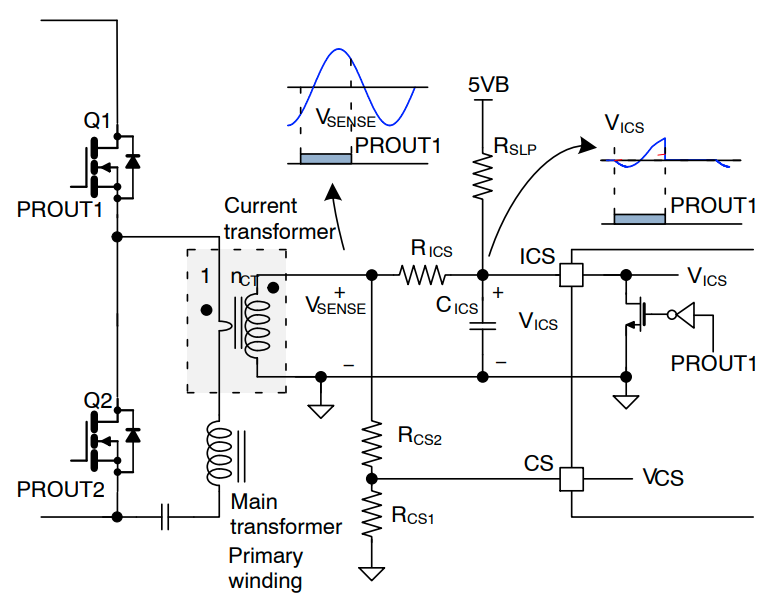
图 25：带斜率补偿的电流检测配置
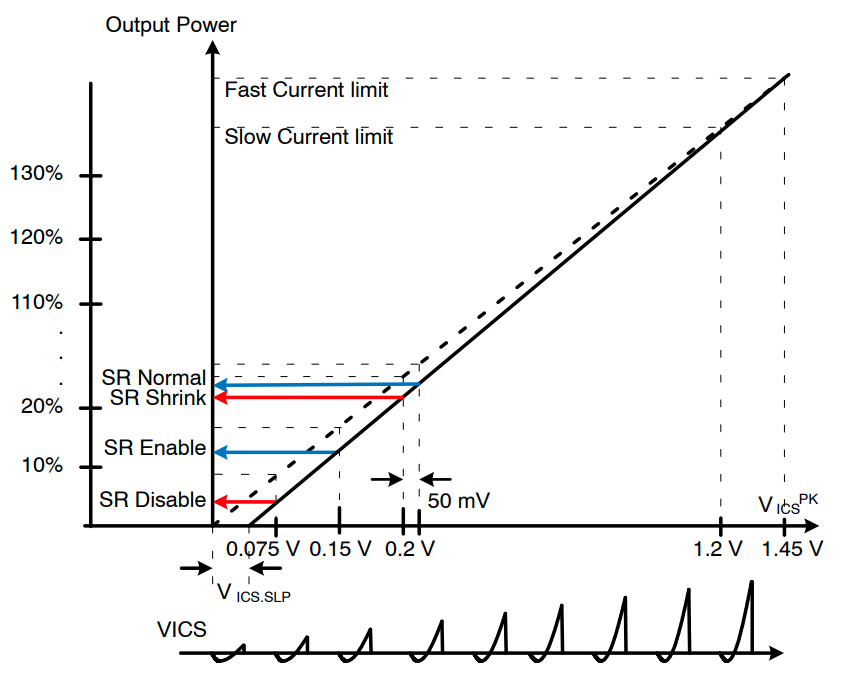
图 26：增加斜率补偿时的负载条件和 ICS 引脚电压
额定输入电压和满载时的初级侧电流峰值由下式估算：
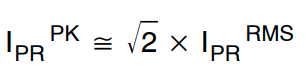（公式37）
RCS1 和 RCS2 之间的比率要根据初级侧过流保护 (OCP) 跳闸点来确定，该跳闸点应小于 IPR PK。
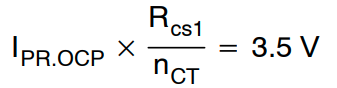
（公式38）
对于匝数比为 44 (nCT) 的电流互感器，RCS1 和 RCS2 之间之和的最小建议值由下式给出：
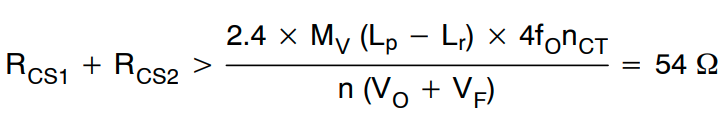
由于功耗不会太高，因此可以将 RCS1 + RCS2 设置得更高，以便在 VICS 上获得理想的积分。由此，我们选择 RCS1 和 RCS2 之和为 230Ω。
额定输入电压和满载条件下的初级侧电流峰值由下式给出：
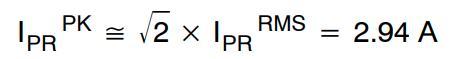
通过将初级侧 OCP 电平设置为 5A，
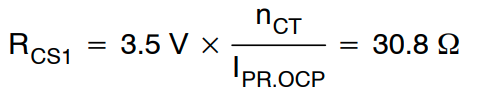
RCS1 和 RCS2 分别选择 30 Ω和 200 Ω。
这种设计不会对 ICS 引脚施加额外的斜率。
将 CICS 选择为 1 nF 电容。假设 1.2 V 时 VICS 的衰减系数为 1.0（图 23 中 x=1.2/10.23 时的读数），则在标称输入电压下提供 13 A 过载保护 (IO.OLP) 的相应 RICS 电阻为
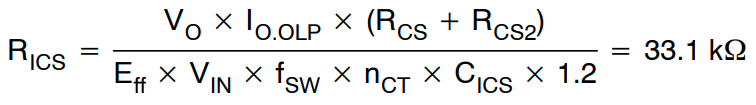
将 RICS 选择为 30 kΩ。
点击文末的“赞”和“在看”，并发送截图和您的邮箱地址到后台，即可领取原版文档哦~
