--关注、星标、回复“40429”--
↓↓领取:《汽车驾驶自动化分级》(GB/T 40429-2021)↓↓
我国智能驾驶车辆起源于1980年,然而在1992年国防科技大学研发真正第一辆智能车。2003年,清华大学研发的THMR-V可在清晰的车道线上完成车道保持,而且它的最高时速可达到150km/h,如图1所示。近几年来随着智能驾驶在全球范围内的不断发展与兴起,我国无论是高校还是企业都在大力发展智能驾驶技术。在2011年,国防科技大和一汽研发的红旗无人驾驶汽车HQ3实现了从长沙到武汉的无人驾驶,标志着我国在无人驾驶方面取得了标志性的进展。2015年12月,百度联合宝马的百度自主车在北京从百度大厦出发,然后绕城到奥林匹克森林公园,最后返回百度大厦。从2015年至今,我国国内的智能驾驶发展在呈爆炸式增长。无论是高校、新兴造车品牌、乘用车、专用车智能驾驶、L4级智能驾驶科技公司、无人配送车、商用车智能驾驶、农机智能驾驶以及矿区智能驾驶正在国内快速发展。诸如新兴品牌的蔚来汽车、理想汽车、小鹏汽车以及传统乘用车的奔驰、大众、比亚迪、丰田等等都在结合自己的优势,并且大力发展智能驾驶技术,同时这些企业已经取得了一定不俗的成绩,如图2所示。从2017年,百度Apollo开发了智能驾驶软件研发平台之后,Apollo生态已经发展的如火如荼。1.2 智能车换道避障运动控制研究现状
对于车辆换道避障来说,换道是前方车辆行驶车速较慢或者车辆处于静止状态,同时旁边车道无切入行为,本车行驶行为无法满足自身需求便产生了换道过程。针对车辆在行驶过程中的换道请求,智能驾驶域控制器通过CAN通信接收模块采集上层传感器信息包含了GPS导航系统、IMU惯性传感器、超声波雷达、激光雷达以及摄像头等传感器信息,并进行数据处理,从而得到最为合适的换道行为并基于车道线规划出一条最优路径。下层控制算法可根据行为决策结果和最优路径,实时求解出方向盘转角并通过CAN通信发送给线控转向系统,从而完成车辆的换道过程。欢迎关注「智驾最前沿」微信视频号
运动控制作为智能车研究关键领域之一,它需要依据周围环境、车辆状态、车速以及车身位姿等信息做出一定的决策,为车辆的驱动、制动以及转向等执行器机构提供一些输入信号,使得车辆可以按照要求进行安全行驶。它主要包含了横向控制和纵向控制,通常以乘客乘坐的舒适性、安全性和车身稳定性作为最为关键的三大指标。其中车辆运动控制器主要包含了车辆模型建立、横向偏差和航向偏差的生成以及控制量等几方面。一般来说车辆模型包含了运动学模型、几何学模型以及动力学模型。目前使用最为广泛的控制方法有:经典控制(PID为例)、最优控制、自适应控制、模型预测控制。PID控制器是智能驾驶领域应用极具广泛的控制算法之一,通常以原理简单容易实现被智能驾驶行业所熟知。2005年的DARPA挑战赛上,Thrun S等设计了PID反馈加曲率前馈的非线性控制器,使得横向偏差收敛至有界值。赵熙俊等利用鲁棒PID反馈控制方法设计了方位偏差估计器实现车辆较好的跟踪效果。LQR(Linear Quadratic Regulator)是使用最为广泛的线性最优控制器。2000年,Sharp提出离散化最优预瞄理论车辆横向LQR控制器建模方法,并实现了车辆良好跟车效果。Park K等为了提高车辆在临界状态下横向稳定性,利用LQR对状态反馈进行估计,并利用非线性观测器对车身侧滑角进行估计,从而得到良好的控制效果。Yang T等提出了前馈+预测LQR的横向控制方法,能较好地适应复杂工况下智能车辆横向跟踪控制问题。LQR方法针对线性系统有效,同时忽略了系统的各类约束条件。模型预测控制方法可根据不同对象和研究目标考虑各种不同的约束条件,非常善于处理非线性系统和含输入输出约束的各类复杂控制问题。Cheng S等提出一种基于模型预测控制方法的横向稳定协调碰撞系统,该系统基于车辆动力学来控制车辆的正常驾驶模式、全自动模式和稳定模式等,实验结果表明该系统具有良好的性能。Gutjahr B等采用线性时变模型预测方案同时结合二次代价函数实现了静态障碍物和动态障碍物的避障,该种方法可适用于不同场景比如静止车辆以及高速公路上动态车辆。Falcone P等提出利用MPC控制转向和制动的路径跟踪方案,它的控制目标是制动和转向联合实现一个较为理想的避障操纵路径。2000年,Choi S B 等利用李雅普诺夫准则提出车辆的横向自适应控制器,搭建用于实时观测反馈参数的横向位移测量器,实验数据说明该控制器具有较强的鲁棒性。在2007年的DARPA挑战赛上,斯坦福大学团队设计了具有学习能力的自适应控制器,并且取得了亚军。Norouzi A等在车辆的换道横向控制中加入了自适应控制,为了防止车辆在行驶过程中的抖动问题。
2.1 引言
路径跟踪通过控制转向角度,实时对规划轨迹进行跟踪。车辆在进行路径跟踪过程中不仅仅要保证跟踪效果具有一定的准确性,同时从驾驶员和乘客的角度出发更要保证车辆在行驶过程中的稳定性及舒适性。路径跟踪的控制算法现阶段较多,其中包括:基于道路几何原理的控制算法,如纯跟踪控制、Stanley控制、Alice控制等;基于经典控制理论的路径跟踪控制算法,如PID控制、线性反馈控制等;基于现代控制理论的路径跟踪控制算法,如MPC控制、LQR控制等。为了选出最为合适的控制方法确保智能车在行驶过程中的安全性、舒适性和稳定性,本文在车辆坐标系下进行了车辆的运动学建模,同时选择三种不同的控制算法使得车辆在同一环境场景下针对三种不同的评价指标进行对比,从而选出最为合适的控制算法。2.2 车辆运动学建模
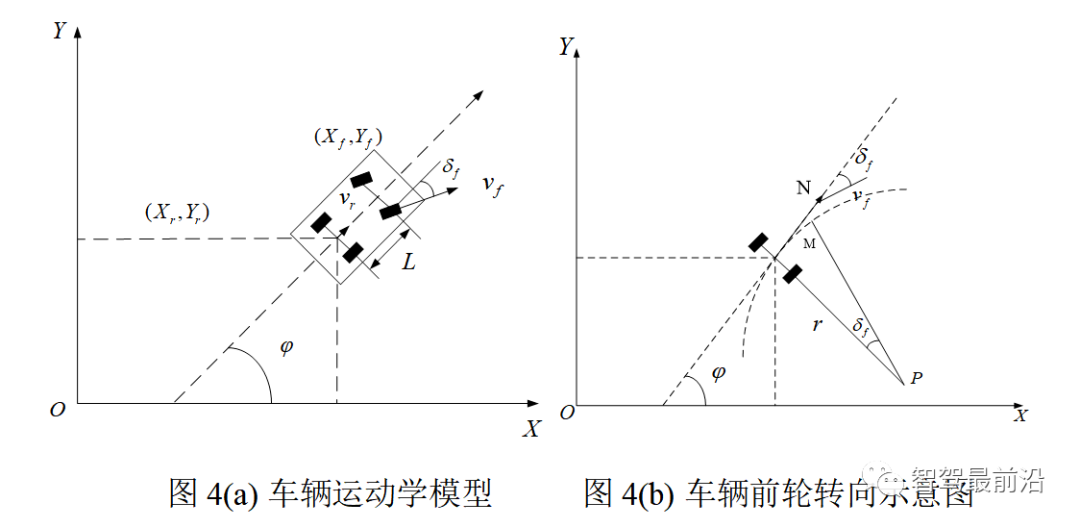
车辆运动学模型如图4(a)所示。在惯性坐标系XOY下,和分别是车辆前轴和后轴的轴心坐标,为车辆的横摆角,为前轮转角,为车辆的后轴中心速度,L为汽车轴距。车辆前轮转向示意图如图4(b)所示,其中M为后轴中心,N为前轴中心,为后轮转向半径,P为车辆瞬动中心。由上图车辆运动学模型可知在后轴 的速度为:
的速度为:2. 3 基于LQR控制算法路径跟踪设计
2.3.1 运动学状态空间模型推导
基于车辆运动学模型(6),可将车辆运动学系统看作成一个输入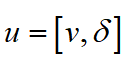 以及状态参数
以及状态参数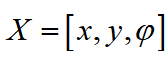 的控制系统。可表示为:上式中
的控制系统。可表示为:上式中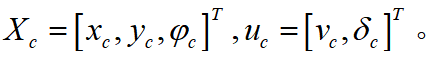 将公式(7)在
将公式(7)在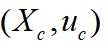 处进行泰勒式展开,忽略最高项,可得:记
处进行泰勒式展开,忽略最高项,可得:记 式(9)与式(8)相互做差得:
式(9)与式(8)相互做差得:2.3.2 LQR控制器设计
上式中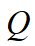 为半正定加权矩阵,
为半正定加权矩阵, 为对称正定矩阵。其中最优控制的目标是对于给定系统在保证一定性能指标下,设计一个控制器
为对称正定矩阵。其中最优控制的目标是对于给定系统在保证一定性能指标下,设计一个控制器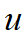 ,使得
,使得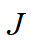 最小。如果所设计的系统是渐近稳定的,则矩阵
最小。如果所设计的系统是渐近稳定的,则矩阵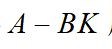 所有特征值具有负实部,根据Lyapunov稳定性定理可得式(15)必然存在正定对称矩阵的二次型Lyapunov函数为
所有特征值具有负实部,根据Lyapunov稳定性定理可得式(15)必然存在正定对称矩阵的二次型Lyapunov函数为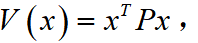 可得:在求取最优控制问题过程中,需要选择一个最为合适的增益矩阵
可得:在求取最优控制问题过程中,需要选择一个最为合适的增益矩阵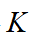 ,可使得其性能指标
,可使得其性能指标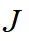 最小化。由式(16)可得只有依赖
最小化。由式(16)可得只有依赖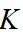 ,且
,且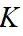 非负,当且仅当可以找到一个对称矩阵
非负,当且仅当可以找到一个对称矩阵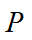 ,满足Riccati方程:
,满足Riccati方程:由上式可证明最优状态反馈控制器
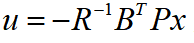
是稳定的。
车辆运动学模型(11)建立之后,可得车辆的运动状态空间方程如式(20)。LQR控制器无法处理
多变量的控制约束问题。即本文不考虑车辆在跟踪路径过程中的其他约束。
其中 为加权矩阵,
为加权矩阵, 为结束位置下的加权矩阵,车辆在
为结束位置下的加权矩阵,车辆在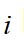 时刻的估计状态为
时刻的估计状态为 ;车辆在期望路径上第
;车辆在期望路径上第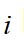 个目标点状态为
个目标点状态为 ;车辆在
;车辆在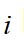 时刻下的控制参量为
时刻下的控制参量为 。对无约束优化问题进行构造,引入拉格朗日乘子:当评价函数最小时,函数
。对无约束优化问题进行构造,引入拉格朗日乘子:当评价函数最小时,函数 满足:已知
满足:已知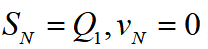 通过后迭代处理得最优反馈控制状态量:上式中
通过后迭代处理得最优反馈控制状态量:上式中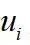 为前馈控制量,
为前馈控制量,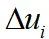 为反馈控制量。
为反馈控制量。2.4 仿真分析
利用Simulink和Prescan进行联合仿真,其中,设定车辆初始时刻和终止时刻行驶过程中车速为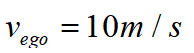 ,路面附着系数
,路面附着系数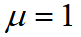 ,单车道路宽度
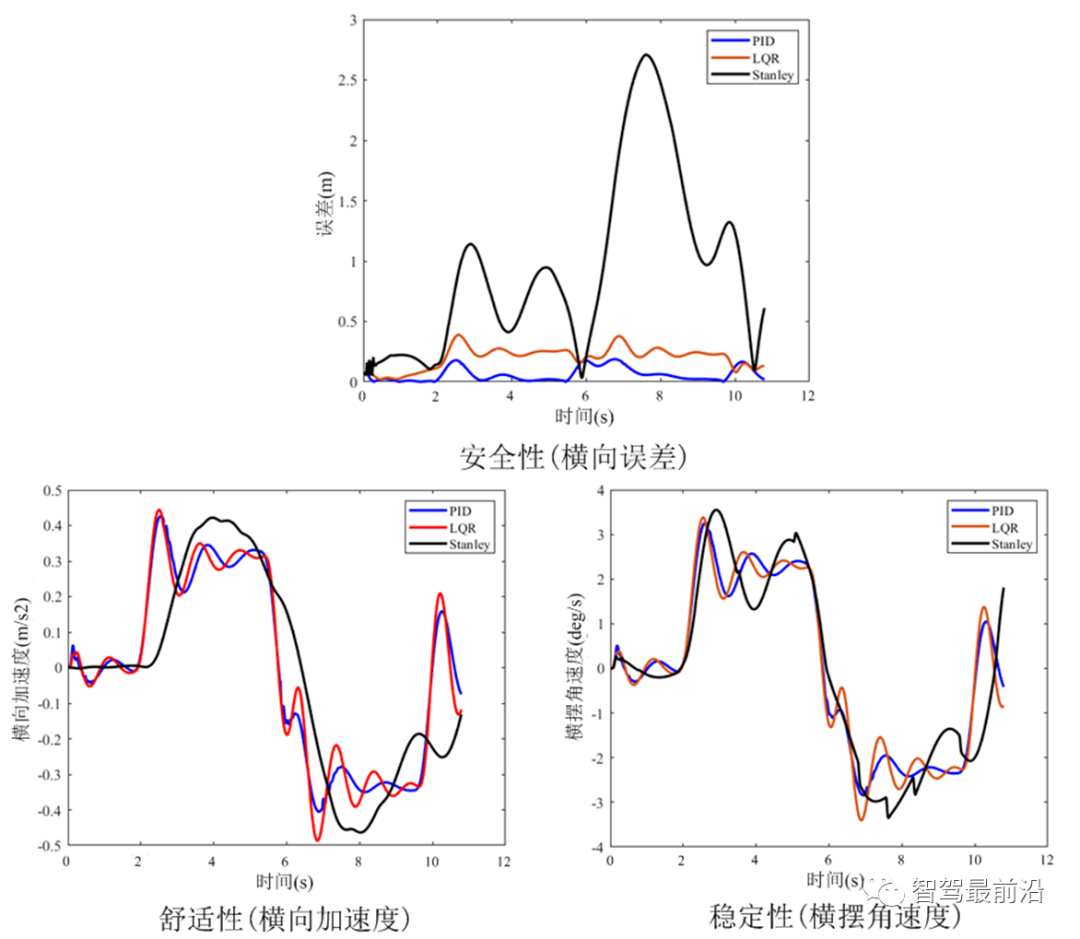
,单车道路宽度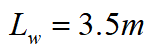 。为了验证本章节所搭建的运动学模型,本文利用三种不同控制方法(PID、Stanley、LQR)实现了车辆的路径跟踪算法设计,并且针对车辆三个性能指标(舒适性、安全性、可靠性)进行分析如图5所示。由上图5可知,针对PID、Stanley和LQR三种不同的控制方法分别从车辆的横向误差、横向加速度和横摆角速度来评判车辆的安全性、舒适性和稳定性。其中,基于经典控制理论的PID路径跟踪控制安全性较好,舒适性中等,稳定性较差;基于道路几何原理的Stanley路径跟踪控制安全性较差,舒适性较好,稳定性较差;基于现代控制理论的LQR路径跟踪控制安全性较好,舒适性中等,稳定性较好。
。为了验证本章节所搭建的运动学模型,本文利用三种不同控制方法(PID、Stanley、LQR)实现了车辆的路径跟踪算法设计,并且针对车辆三个性能指标(舒适性、安全性、可靠性)进行分析如图5所示。由上图5可知,针对PID、Stanley和LQR三种不同的控制方法分别从车辆的横向误差、横向加速度和横摆角速度来评判车辆的安全性、舒适性和稳定性。其中,基于经典控制理论的PID路径跟踪控制安全性较好,舒适性中等,稳定性较差;基于道路几何原理的Stanley路径跟踪控制安全性较差,舒适性较好,稳定性较差;基于现代控制理论的LQR路径跟踪控制安全性较好,舒适性中等,稳定性较好。2.5 小结
车辆横向运动过程中最为主要的评价指标为安全性、稳定性和舒适性。从这三种评价指标入手,构建车辆运动学模型利用三种不同控制算法在同一道路工况进行路径跟踪仿真测试。测试结果表明:基于现代控制理论的LQR控制算法相对PID控制来说稳定性较好且调试过程方便简单;相对基于道路几何的Stanley来说安全性和稳定性较好。转载自智能运载装备研究所,文中观点仅供分享交流,不代表本公众号立场,如涉及版权等问题,请您告知,我们将及时处理。
-- END --



 的速度为:
的速度为:
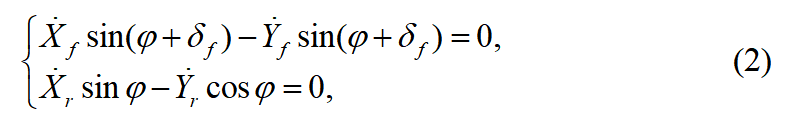



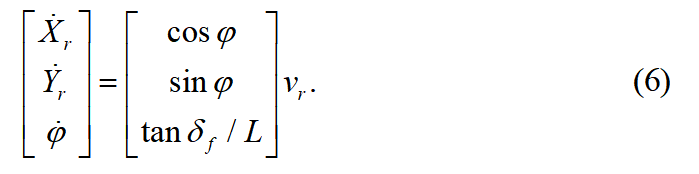
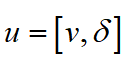 以及状态参数
以及状态参数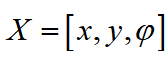 的控制系统。可表示为:
的控制系统。可表示为:

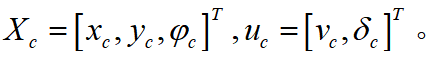 将公式(7)在
将公式(7)在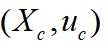 处进行泰勒式展开,忽略最高项,可得:
处进行泰勒式展开,忽略最高项,可得: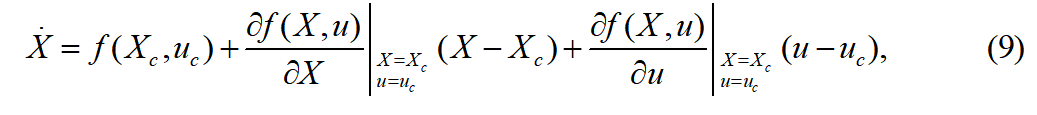
 式(9)与式(8)相互做差得:
式(9)与式(8)相互做差得: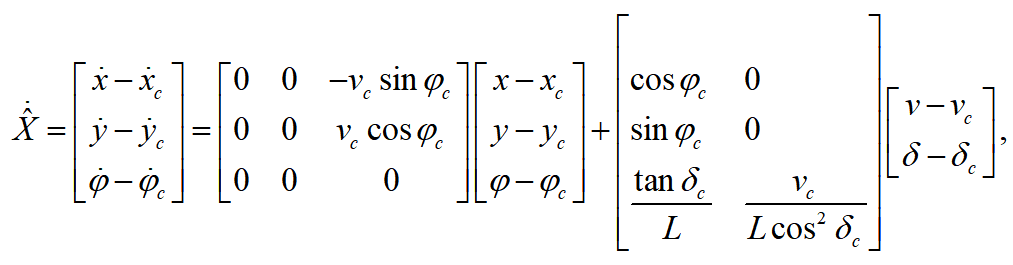
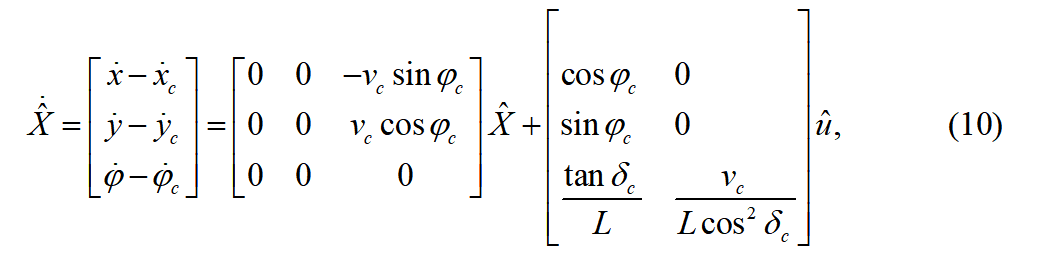
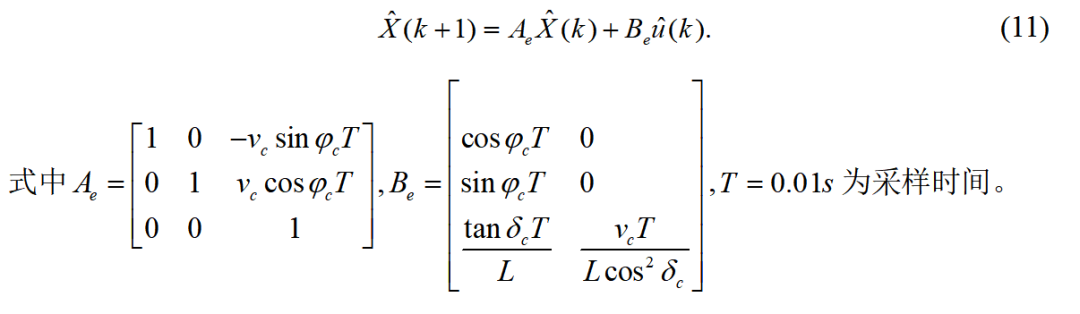

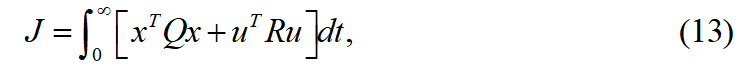
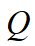 为半正定加权矩阵,
为半正定加权矩阵, 为对称正定矩阵。其中最优控制的目标是对于给定系统在保证一定性能指标下,设计一个控制器
为对称正定矩阵。其中最优控制的目标是对于给定系统在保证一定性能指标下,设计一个控制器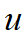 ,使得
,使得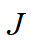 最小。
最小。

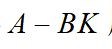 所有特征值具有负实部,根据Lyapunov稳定性定理可得式(15)必然存在正定对称矩阵的二次型Lyapunov函数为
所有特征值具有负实部,根据Lyapunov稳定性定理可得式(15)必然存在正定对称矩阵的二次型Lyapunov函数为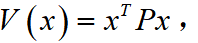 可得:
可得:
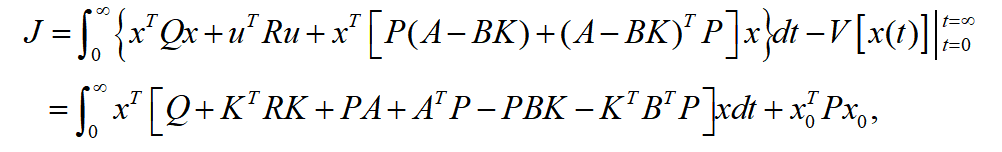
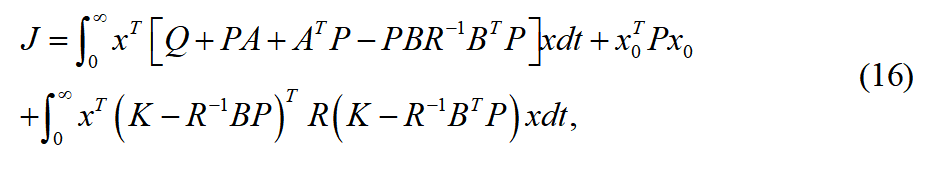
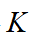 ,可使得其性能指标
,可使得其性能指标 最小化。由式(16)可得只有依赖
最小化。由式(16)可得只有依赖 ,且
,且 非负,当且仅当可以找到一个对称矩阵
非负,当且仅当可以找到一个对称矩阵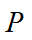 ,满足Riccati方程:
,满足Riccati方程:


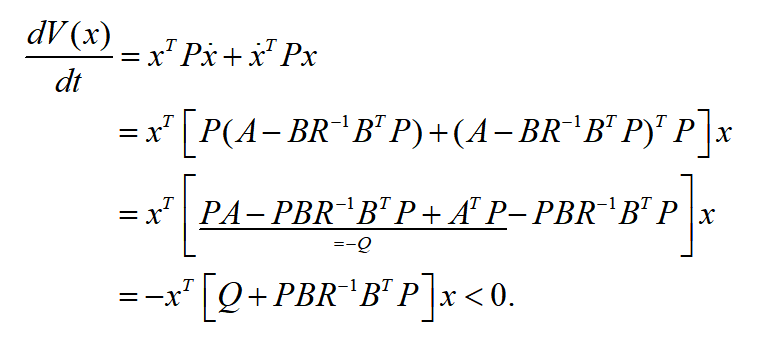
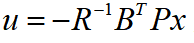

 为车辆在路径跟踪过程中当前状态下的状态量与期望位置状态量的偏差大小,
为车辆在路径跟踪过程中当前状态下的状态量与期望位置状态量的偏差大小, 。
。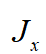 和
和 是函数
是函数 关于
关于 的雅可比矩阵。定义指标:
的雅可比矩阵。定义指标: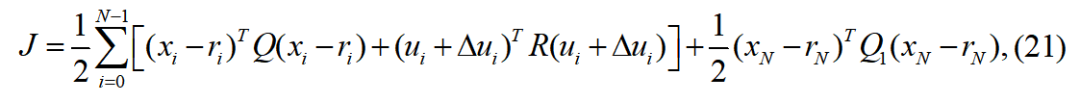
 为加权矩阵,
为加权矩阵, 为结束位置下的加权矩阵,车辆在
为结束位置下的加权矩阵,车辆在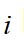 时刻的估计状态为
时刻的估计状态为 ;车辆在期望路径上第
;车辆在期望路径上第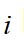 个目标点状态为
个目标点状态为 ;车辆在
;车辆在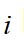 时刻下的控制参量为
时刻下的控制参量为 。对无约束优化问题进行构造,引入拉格朗日乘子:
。对无约束优化问题进行构造,引入拉格朗日乘子: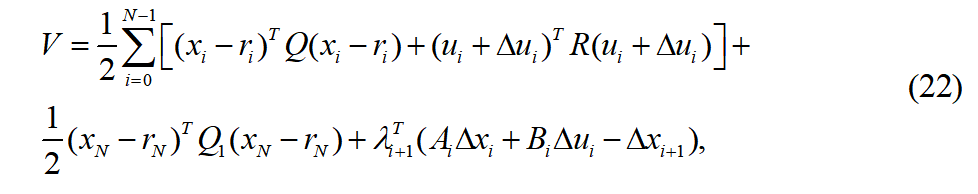
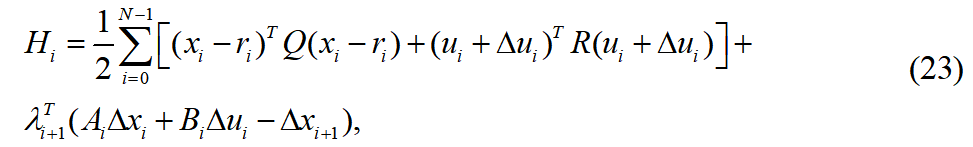
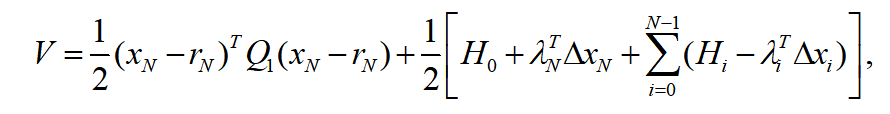
 满足:
满足: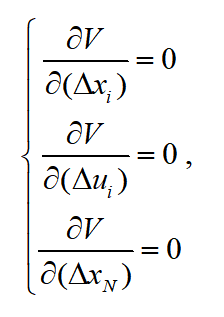
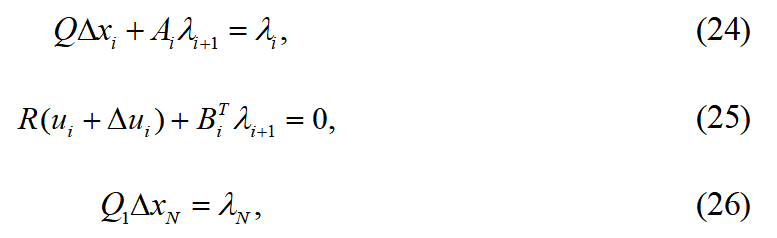

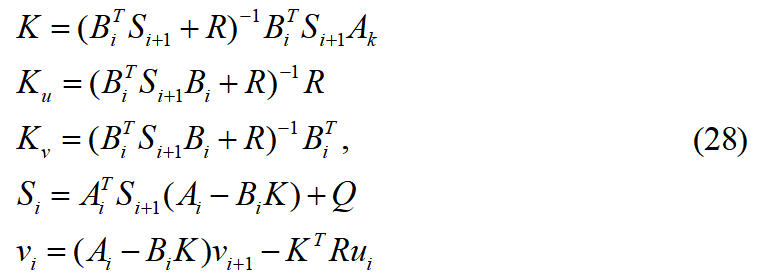
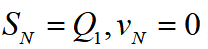 通过后迭代处理得最优反馈控制状态量:
通过后迭代处理得最优反馈控制状态量: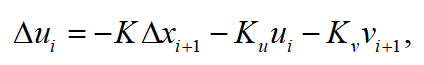
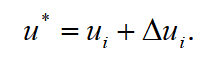
 为前馈控制量,
为前馈控制量, 为反馈控制量。
为反馈控制量。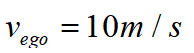 ,路面附着系数
,路面附着系数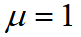 ,单车道路宽度
,单车道路宽度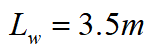 。
。