--关注、星标、回复“自主泊车”--
对于自动驾驶应用来说,最终还是需要对3D场景进行感知。道理很简单,车辆不能靠着一张图像上得到感知结果来行驶,就算是人类司机也不能对着一张图像来开车。因为物体的距离和场景的和深度信息在2D感知结果上是体现不出来的,而这些信息才是自动驾驶系统对周围环境作出正确判断的关键。
一般来说,自动驾驶车辆的视觉传感器(比如摄像头)安装在车身上方或者车内后视镜上。无论哪个位置,摄像头所得到的都是真实世界在透视视图(Perspective View)下的投影(世界坐标系到图像坐标系)。这种视图与人类的视觉系统很类似,因此很容易被人类驾驶员理解。但是透视视图有一个致命的问题,就是物体的尺度随着距离而变化。因此,当感知系统从图像上检测到了前方有一个障碍物时,它并不知道这个障碍物距离车辆的距离,也不知道障碍物的实际三维形状和大小。
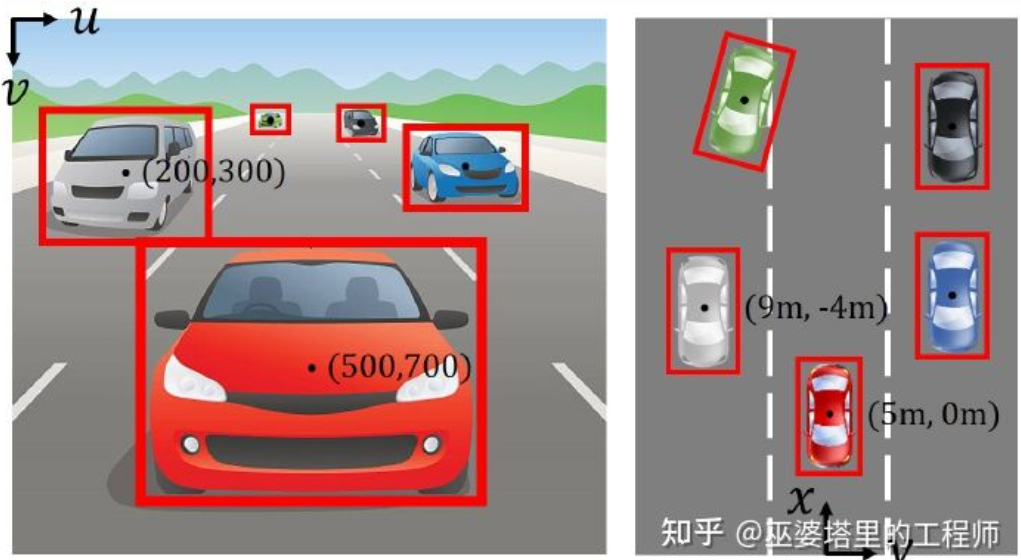
图像坐标系(透视视图)vs. 世界坐标系(鸟瞰视图)[IPM-BEV]
想要得到3D空间的信息,一个最直接的方法就是采用激光雷达(LiDAR)。一方面,LiDAR输出的3D点云可以直接用来获取障碍物的距离和大小(3D物体检测),以及场景的深度(3D语义分割)。另一方面,3D点云也可以与2D图像进行融合,以充分利用两者所提供的不同信息:点云的优势在于距离和深度感知精确,而图像的优势在于语义信息更加丰富。
但是,LiDAR也有其缺点,比如成本较高,车规级产品量产困难,受天气影响较大等等。因此,单纯基于摄像头的3D感知仍然是一个非常有意义和价值的研究方向。本文以下的部分会详细介绍基于单摄像头和双摄像头的3D感知算法。
基于单摄像头图像来感知3D环境是一个病态问题,但是可以利用一些几何约束和先验知识来辅助完成这个任务,也可以采用深度神经网络端对端的学习如何从图像特征来预测3D信息。

单摄像头3D物体检测(图片来自M3D-RPN)
图像反变换
前面提到,图像是从真实世界的3D坐标到2D平面坐标的投影,因此从图像来进行3D物体检测的一个很直接的思路就是将2D图像反变换到3D世界坐标,然后在世界坐标系下进行物体检测。理论上说这是一个病态问题,但是可以通过一些额外信息(比如深度估计)或者几何假设(比如像素位于地面)来辅助解决。
BEV-IPM[1]中提出将图像从透视视图转换到鸟瞰视图(BEV)。这里有两个假设:一是路面与世界坐标系平行并且高度为零,二是车辆自身的坐标系与世界坐标系平行。前者在路面非平坦的情况下并不满足,后者则可以通过车辆姿态参数(Pitch和Roll)来校正,其实就是车辆坐标系和世界坐标系的Calibration。假设图像中所有像素在真实世界的高度都为零,那么就可以采用Homography变换将图像转换到BEV视图。在BEV视图下采用基于YOLO网络的方法检测目标的Bottom Box,也就是与路面接触部分的矩形。Bottom Box的高度为零,因此可以准确的投影到BEV视图上作为GroudTruth来训练神经网络,同时神经网络预测的Box也可以准确的估计其距离。这里的假设是目标需要与路面接触,这对于车辆和行人目标来说一般是满足的。
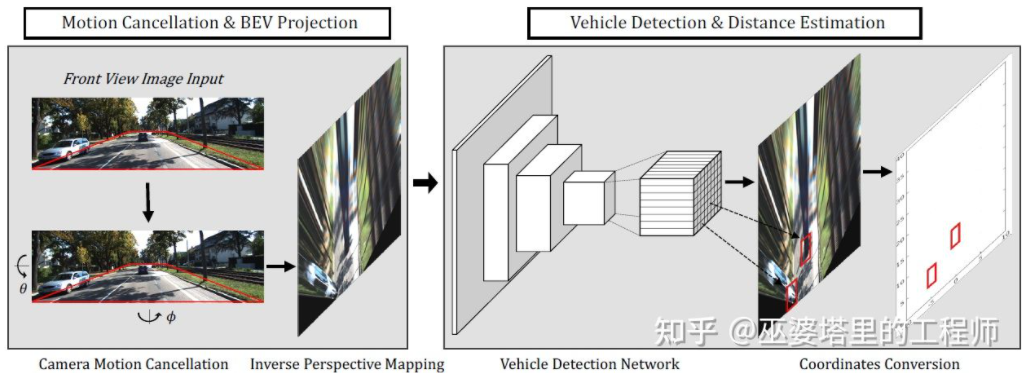
BEV-IPM
另外一种反变换的方法采用Orthographic Feature Transform (OFT)[2]。其思路是采用CNN提取多尺度的图像特征,然后将这些图像特征变换到BEV视图,最后在BEV特征上进行3D物体检测。首先需要构建BEV视角下的3D网格(文中实验的网格范围为80米x80米x4米,网格大小为0.5m)。每个网格通过透视变换对应图像上的一块区域(简单起见就定义为矩形区域),将这个区域内的图像特征的均值作为该网格的特征,这样就得到了3D网格特。为了减小计算量,3D网格特征在高度这一维上进行压缩(加权平均),得到2D网格特征。最终的物体检测在2D网格特征上进行。3D网格到2D图像像素的投影并不是一一对应的,多个网格会对应临近的图像区域,导致网格特征出现歧义性。所以这里也需要假设待检测的物体都在路面上,高度的范围很窄。所以文中实验采用了的3D网格高度只有4米,这足以覆盖地面上的车辆和行人。但是如果要检测交通标志的话,这类假设物体都贴近地面的方法就不适用了。
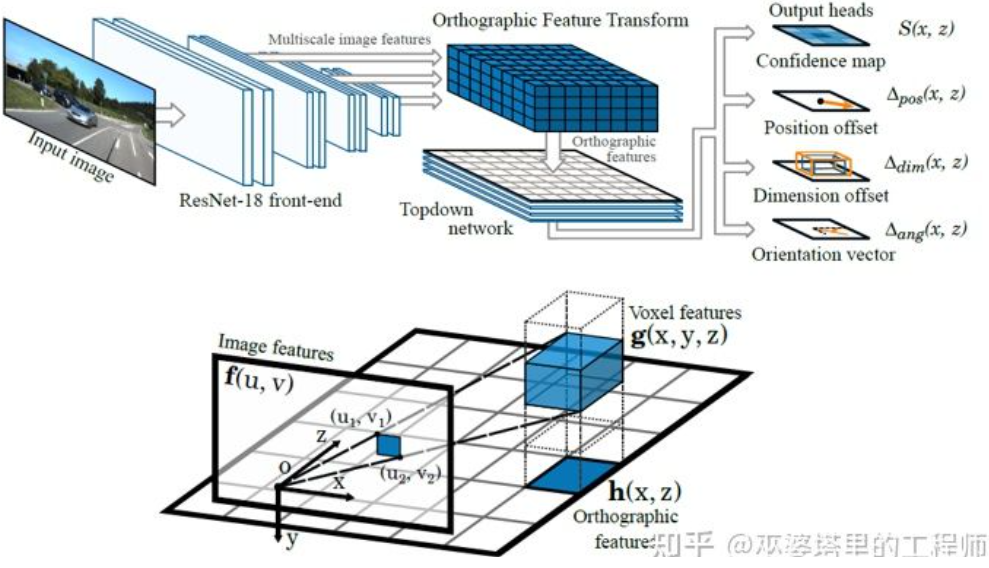
Orthographic Feature Transform
以上这个两个方法都是基于物体位于地面的假设。除此之外,另外一个思路是采用深度估计的结果来生成伪点云数据,其中一个典型的工作就是Pseudo-LiDAR[3]。深度估计的结果一般被看作额外的图像通道(类似RGB-D数据),基于图像的物体检测网络被直接用来生成3D物体边框。作者在文章中指出,基于深度估计的3D物体检测之所以准确度比基于LiDAR的方法差很多,主要原因不在于深度估计的精度不够,而是在于数据表示的方法有问题。首先,在图像数据上,远处的物体面积非常小,这使得远处物体的检测非常不准确。其次,深度上相邻像素的深度差可能是非常大的(比如在物体的边缘处),此时采用卷积操作来提取特征就会有问题。考虑到这两点,作者提出依据深度图将输入图像转换为类似LiDAR生成的点云数据,然后采用点云和图像融合的算法(比如AVOD和F-PointNet)来检测3D物体。Pseudo-LiDAR的方法并不依赖于特定的深度估计算法,任何来自单目或双目的深度估计都可以直接使用。通过这种特殊的数据表示方法,Pseudo-LiDAR在30米范围内可以将物体检测的准确率从22%提高到74%。

Pseudo-LiDAR
与真实的LiDAR点云相比,Pseudo-LiDAR方法在3D物体检测的准确率上还是有着一定的差距,这主要是由于深度估计的精度不够导致的(双目比单目效果好一些),尤其是物体周边的深度估计误差会对检测带来很大的影响。因此,Pseudo-LiDAR之后也进行了很多扩展。Pseudo-LiDAR++[4]采用低线束的LiDAR来增强虚拟的点云。Pseudo-Lidar End2End[5]采用实例分割来代替F-PointNet中的物体框。RefinedMPL[6]只在前景点上生成虚拟点云,将点云的数量降低到原来的10%,可以有效地降低误检的数量和算法的计算量。
关键点和3D模型
在自动驾驶应用中,很多需要检测的目标(比如车辆和行人)其大小和形状相对比较固定,而且是已知的。这些先验知识可以被用来估计目标的3D信息。
DeepMANTA[7]是这个方向的开创性工作之一。首先,采用传统的图像物体检测算法比如Faster RNN来得到2D的物体框,同时也检测车辆上的关键点。然后,将这些2D物体框和关键点与数据库中的多种3D车辆CAD模型分别进行匹配,选择相似度最高的模型作为3D物体检测的输出。
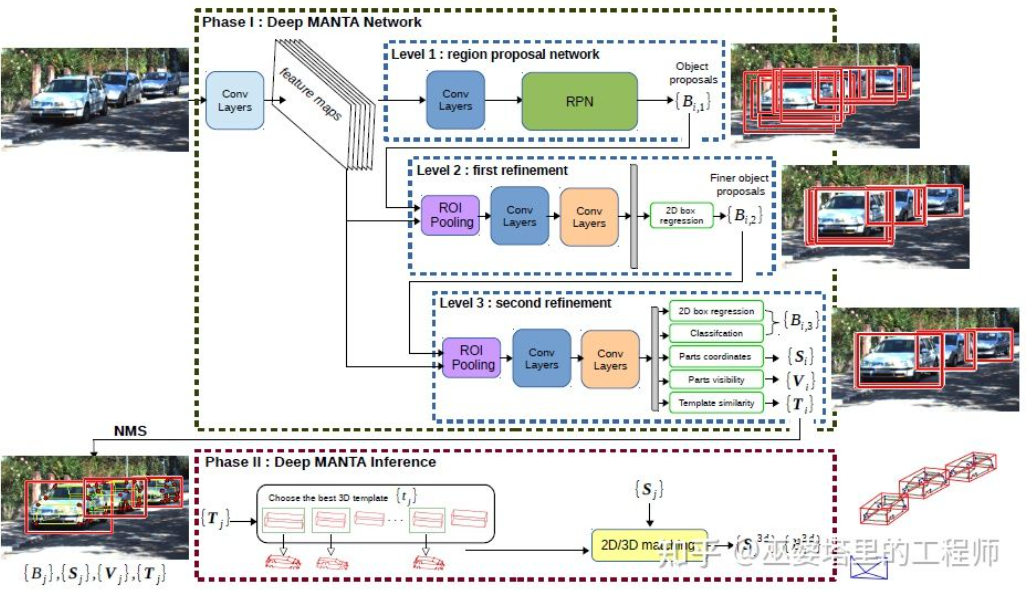
Deep MANTA
3D-RCNN[8]提出采用Inverse-Graphics方法,基于图像来恢复场景中各个目标的3D形状和姿态。其基本思路是从目标的3D模型出发,通过参数搜索找到与图像中的目标最匹配的模型。这些3D模型通常都有很多控制参数,搜索空间很大,因此传统的方法在高维参数空间搜索最优效果并不好。3D-RCNN采用PCA对参数空间进行降维(10-D),并且利用深度神经网络(R-CNN)来预测每个目标的低维模型参数。预测的模型参数可以用来生成每个目标的二维图像或者深度图,与GroudTruth数据对比得到的Loss可以用来指导神经网络的学习。这个Loss称之为Render-and-Compare Loss,是基于OpenGL来实现的。3D-RCNN方法需要的输入数据比较多,Loss的设计也相对复杂,工程实现上难度较大。
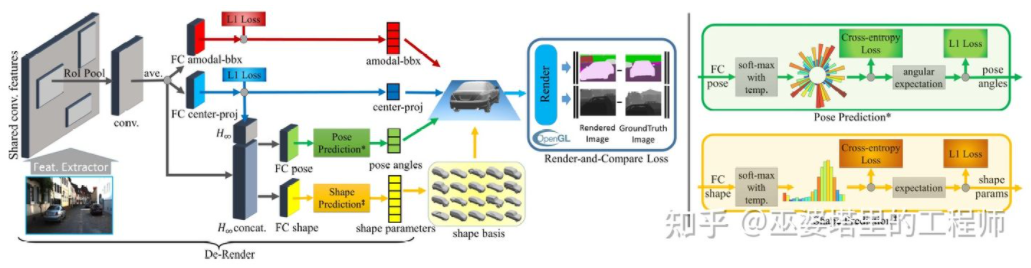
3D-RCNN
MonoGRNet[9]提出将单目3D物体检测分成四个步骤,分别用来预测2D物体框,物体3D中心的深度,物体3D中心的2D投影位置和8个角点的3D位置。首先,图像中预测的2D物体框通过ROIAlign操作,得到物体的视觉特征。然后,而这些特征被用来预测物体3D中心的深度和3D中心的2D投影位置。有了这两个信息后,就可以得到物体3D中心点的位置。最后,根据3D中心的位置再来预测8个角点的相对位置。MonoGRNet可以被认为是只采用物体中心的作为关键点,2D和3D的匹配也就是点距离的计算。MonoGRNetV2[10]将中心点扩展到多个关键点,并采用3D CAD物体模型来进行深度估计,这与之前介绍的DeepMANTA和3D-RCNN就很类似了。
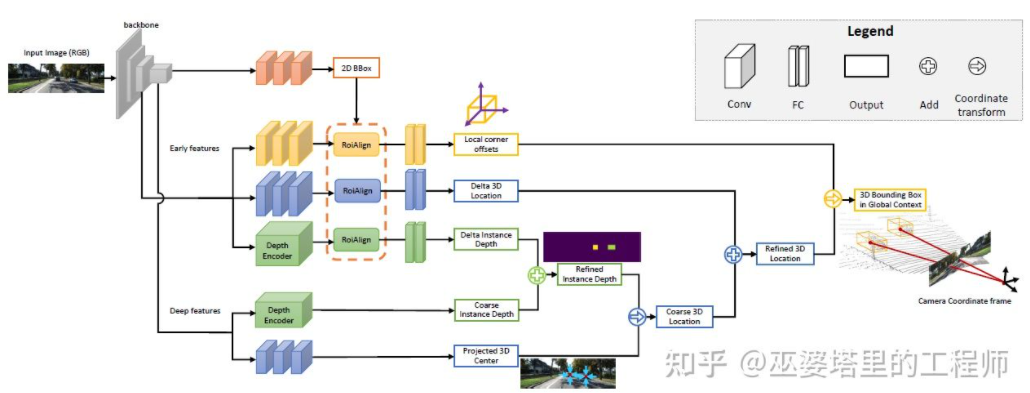
MonoGRNet
Monoloco[11]主要解决行人的3D检测问题。行人是非刚性物体,姿态和变形也更加多样,因此比车辆检测更加具有挑战性。Monoloco也是基于关键点检测,关键点先验的相对3D位置可以被用来进行深度估记。比如,以行人肩部到臀部50厘米的长度为基准来估计行人的距离。以此长度作为基准的原因是,人体的这个部分可以产生的变形最小,用来做深度估记准确度也最高。当然,其他的关键点也可以作为辅助共同来完成深度估记的任务。Monoloco采用多层全连接网络,从关键点的位置来预测一个行人的距离,同时也给出预测的不确定性。
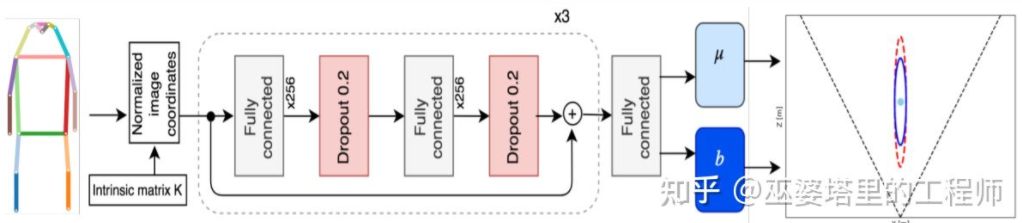
Monoloco
总结一下,以上方法都是从2D图像中提取关键点,并且与3D模型进行匹配,从而得到目标的3D信息。这类方法假设目标有相对固定的形状模型,对于车辆来说一般是满足的,对于行人来说就相对困难一些。此外,这类方法需要在2D图像上标注多个关键点,这也是非常费时的。
2D/3D几何约束
Deep3DBox[12]是这个方向早期的并且很有代表性的工作。3D物体框需要9维变量来表示,分别是中心,大小和朝向(3D朝向可以简化为Yaw,因此变为7维变量)。图像2D物体检测可以提供2D物体框,包含4个已知变量(2D中心和2D大小),这不足以求解具有7维或者9维自由度的变量。在这三组变量中,大小和朝向与视觉特征的关系相对紧密。比如物体的3D大小与其类别(行人,自行车,小轿车,公交车,卡车等)相关性非常大,而物体类别是可以通过视觉特征来预测的。对于中心点3D位置来说,由于透视投影产生的歧义性,单纯通过视觉特征是很难预测的。因此,Deep3DBox提出首先用2D物体框内的图像特征来估计物体大小和朝向。然后,再通过一个2D/3D的几何约束来求解中心点3D位置。这个约束就是3D物体框在图像上的投影是被2D物体框紧密的包围的,也就是在2D物体框的每条边上都至少能找到一个3D物体框的角点。通过之前已经预测的大小和朝向,再配合上相机的Calibration参数,就可以求解中心点的3D位置。
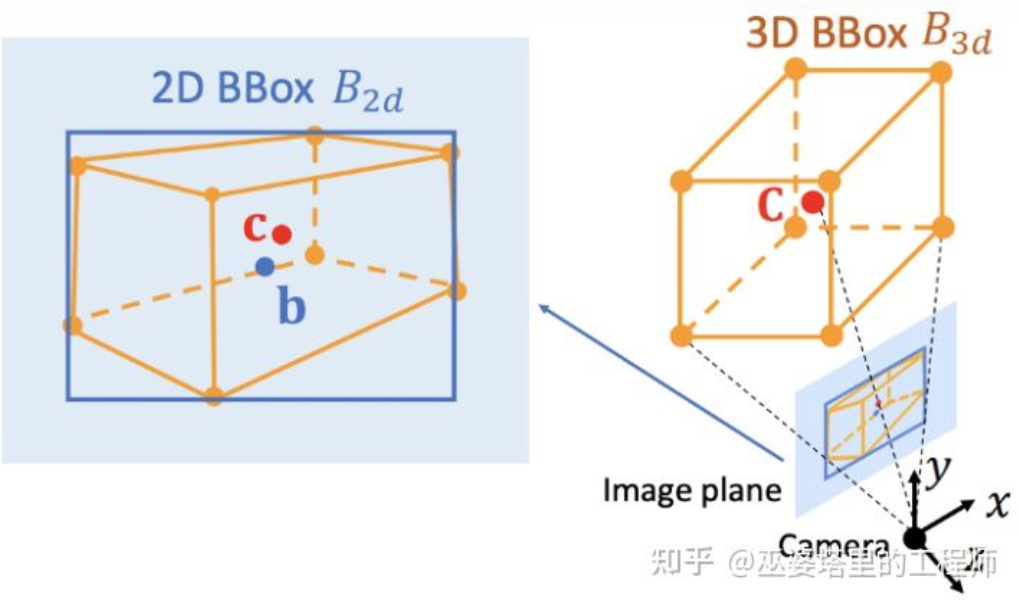
2D和3D物体框之间的几何约束(图片来源于文献[9])
这种利用2D/3D约束的方法需要非常精确的2D物体框检测。在Deep3DBox的框架下,2D物体框上很小的误差都可能会导致3D物体框预测的失败。Shift R-CNN[13]的前两个阶段与Deep3DBox非常相似,都是通过2D物体框和视觉特征来预测3D大小和朝向,然后通过几何约束来求解3D位置。但是,Shift R-CNN增加了第三个阶段,将前两个阶段得到的2D物体框,3D物体框以及相机参数合并起来作为输入,采用全连接网络预测更为精确的3D位置。
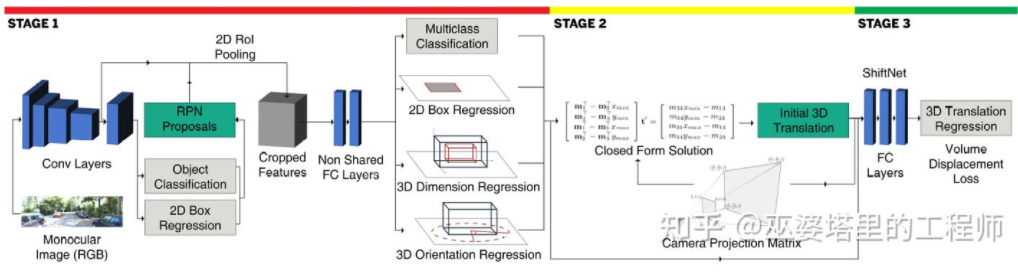
Shift R-CNN
在利用2D/3D几何约束时,上述方法都是通过求解一组超约束方程来得到物体的3D位置,而这个过程是作为一个后处理步骤,并不在神经网络之内。Shift R-CNN的第一和第三阶段也是分开训练的。MVRA[14]将这个超约束方程的求解过程建成一个网络,并设计了图像坐标下的IoU Loss和BEV坐标下的L2 Loss分别来衡量物体框和距离估计的误差,以辅助完成端对端的训练。这样一来,物体3D位置预测的质量也会对之前的3D大小和朝向预测产生反馈作用。
直接生成3D物体框
之前介绍的三类方法都是从2D图像出发,有的将图像变换到BEV视图,有的检测2D关键点并与3D模型匹配,还有的采用2D和3D物体框的几何约束。除此之外,还有一类方法从稠密的3D物体候选出发,通过2D图像上的特征对所有的候选框进行评分,评分高的候选框既是最终的输出。这种策略有些类似物体检测中传统的Sliding Window方法。
Mono3D[15]是这类方法中的代表。首先,基于目标先验位置(z坐标位于地面)和大小来生成稠密的3D候选框。在KITTI数据集上,每帧大约生成40K(车辆)或70K(行人和自行车)个候选框。这些3D候选框投影到图像坐标后,通过2D图像上特征进行评分。这些特征来自语义分割,实例分割,上下文,形状以及位置先验信息。所有这些特征融合起来对候选框进行评分,然后选出分数较高的作为最终的候选。这些候选再通过CNN再进行下一轮的评分,以得到最终的3D物体框。
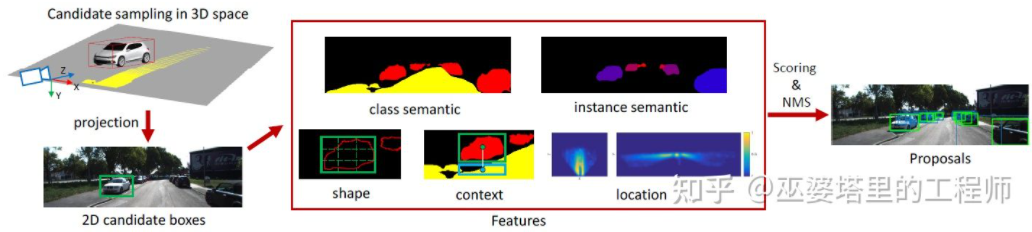
Mono3D
M3D-RPN[16]是一种基于Anchor的方法。该方法定义了2D和3D的Anchor,分别表示2D和3D物体框。2D Anchor通过图像上稠密采样得到,而3D Anchor的参数是基于通过训练集数据得到的先验知识确定的。具体来说,每个2D Anchor与图像中标注的2D物体框按照IoU进行匹配,对应的3D物体框的均值用来定义3D Anchor的参数。值得一提的是,M3D-RPN中同时采用了标准卷积操作(具有空间不变性)和Depth-Aware卷积。后者将图像的行(Y坐标)分成多个组,每个组对应不同的场景深度,采用不同的卷积核来处理。
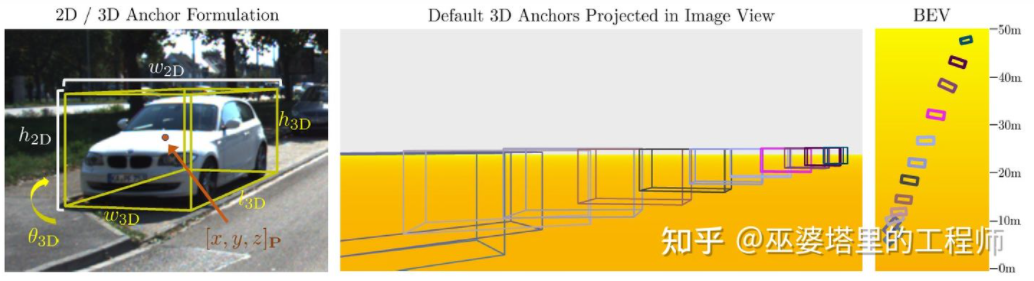
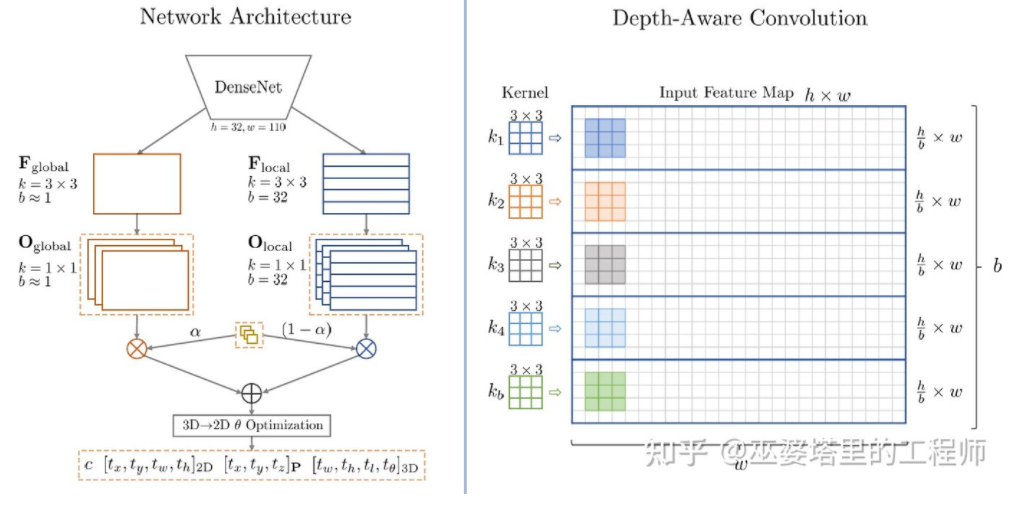
M3D-RPN中的Anchor设计和Depth-Aware卷积
虽然利用了一些先验知识,Mono3D和M3D-RPN生成物体候选或者Anchor时还是基于稠密采样的方式,因此需要的计算量非常大,实用性受到很大影响。后续一些方法提出采用二维图像上检测结果来进一步减少搜索的空间。
TLNet[17]在二维平面密集的放置Anchor。Anchor间隔为0.25米,朝向为0度和90度,大小为目标的平均值。图像上的二维检测结果在三维空间内形成多个视锥,通过这这些视锥可以过滤掉大量背景上的Anchor,从而提高算法的效率。过滤后的Anchor投影到图像上,进行ROI Pooling后得到的特征用来进一步细化3D物体框的参数。
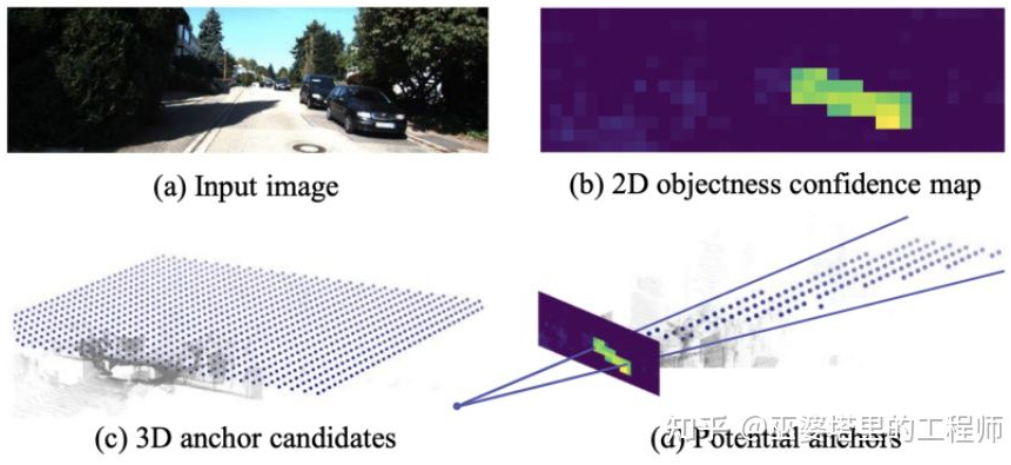
TLTNet
SS3D[18]则采用更为高效的单阶段检测,用类似于CenterNet结构的网络直接从图像输出多种2D和3D信息,比如物体类别,2D物体框,3D物体框。需要注意的是,这里的3D物体框并不是一般的9D或7D表示(这种表示很难直接从图像预测),而是采用更容易从图像预测也包含更多冗余的2D表示,包括距离(1-d),朝向(2-d,sin和cos),大小(3-d),8个角点的图像坐标(16-d)。再加上2D物体框的4-d表示,一共是26D的特征。所有这些特征都被用来进行3D物体框的预测,预测的过程其实就是找到一个与26D特征最为匹配3D物体框。比较特殊的一点是,这个求解的过程是在神经网络内部进行,所以必须是可导的,这也是该文章一个主要亮点。受益于简单的结构和实现,SS3D的运行速度可以达到20FPS。
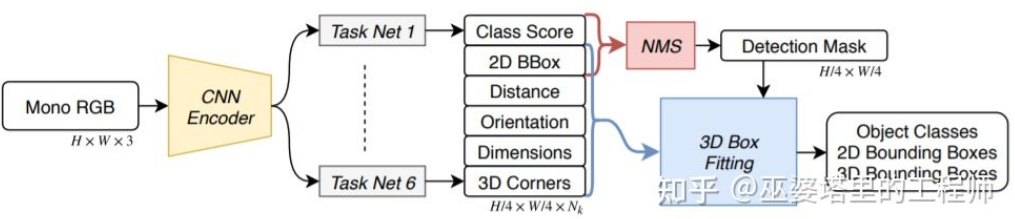
SS3D
FCOS3D[19]也是一个单阶段的检测方法,但是比SS3D更加简洁。3D物体框的中心投影到2D图像,得到2.5D中心(X,Y,Depth),以此作为回归的目标之一。此外,回归的目标还有3D大小和朝向。这里的朝向采用角度(0-pi)+heading联合的方式来表示。
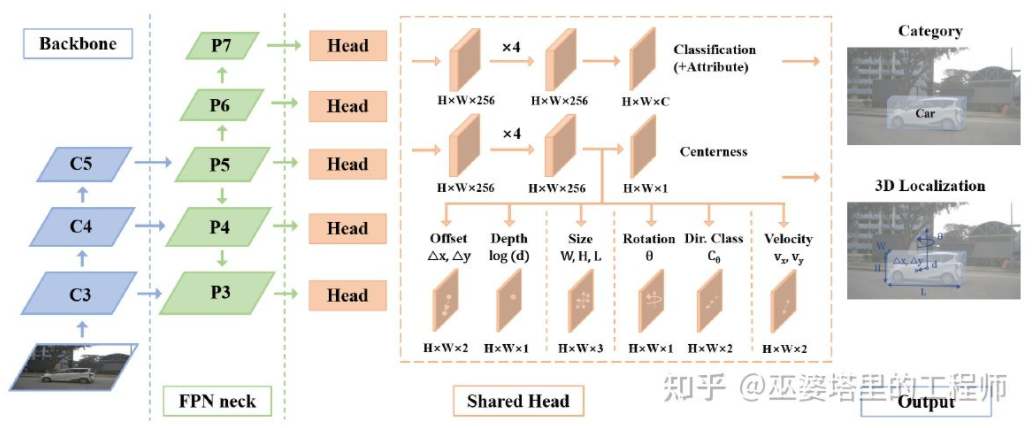
FCOS3D
SMOKE[20]也提出了类似的思路,通过类似CenterNet的结构从图像直接预测2D和3D信息。2D信息包括物体关键点(中心点和角点)在图像上的投影位置,3D信息包括中心点深度,尺寸和朝向。通过中心点的图像位置和深度,可以恢复物体的3D位置。再通过3D尺寸和朝向可以恢复各个角点的3D位置。
以上介绍的这几种单阶段网络的思路就是直接从图像回归3D信息,不需要复杂的前处理(比如图像反变换)和后处理(比如3D模型匹配),也不需要精确的几何约束(比如2D物体框的每条边上都至少能找到一个3D物体框的角点)。这些方法只用到了少量的先验知识,比如各类物体实际大小的均值,以及由此得到的2D物体尺寸与深度的对应关系。这些先验知识定义了物体3D参数的初始值,而神经网络只需要回归与实际值的偏差即可,这就大大降低的搜索空间,也因此降低了网络学习的难度。
上一小节里介绍了单目3D物体检测的代表性方法,其思路从早期的图像变换,3D模型匹配和2D/3D几何约束,到近期的直接通过图像预测3D信息。这种思路上的变化很大程度上来源于卷积神经网在深度估计上的进展。之前介绍的单阶段3D物体检测网络中大多都包含了深度估计的分支。这里的深度估计虽然只是在稀疏的目标级别,而不是稠密的像素级别,但是对于物体检测来说已经足够了。
除了物体检测,自动驾驶感知还有另外一个重要任务,那就是语义分割。语义分割从2D扩展到3D,一种最直接的方式就是采用稠密的深度图,这样每个像素点的语义和深度信息就都有了。
综合以上两点,单目深度估计在3D感知任务中起到了非常重要的作用。从上一节3D物体检测方法的介绍可以类推,全卷积的神经网络也可以用来进行稠密的深度估计。下面我们来介绍一下这个方向的发展现状。
单目深度估计的输入是一张图像,输出也是一张图像(一般与输入相同大小),其上的每个像素值对应输入图像的场景深度。这个任务有些类似图像语义分割,只不过语义分割输出的是每个像素的语义分类。当然,输入也可以是视频序列,利用相机或者物体运动带来的额外信息来提高深度估计的准确度(对应视频语义分割)。
前面提到过,从2D图像预测3D信息是一个病态问题,因此传统的方法会利用几何信息,运动信息等线索,通过手工设计的特征来预测像素深度。与语义分割类似,超像素(SuperPixel)和条件随机场(CRF)这两个方法也经常被用来提高估计的精度。近年来,深度神经网络在各种图像感知任务上都取得了突破性的进展,深度估计当然也不例外。大量的工作都表明,深度神经网络可以通过训练数据学习到比手工设计更加优越的特征。这一小节主要介绍这种基于监督学习的方法。其它一些非监督学习的思路,比如利用双目的视差信息,单目双像素(Dual Pixel)的差异信息,视频的运动信息等等,留待后面再来介绍。
这个方向早期的一个代表性工作是由Eigen等人提出的基于全局和局部线索融合的方法[21]。单目深度估计歧义性主要来自于全局的尺度。比如,文中提到一个真实的房间和一个玩具房间可能从图像上看来差别很小,但是实际的景深却差别很大。虽然这是一个极端的例子,但是真实的数据集中依然存在房间和家具尺寸的变化。因此,该方法提出将图像进行多层卷积和下采样,得到整个场景的描述特征,并以此来预测全局的深度。然后,通过另外一个局部分支(相对较高的分辨率)来预测图像局部的深度。这里全局深度会作为局部分支的一个输入来辅助局部深度的预测。
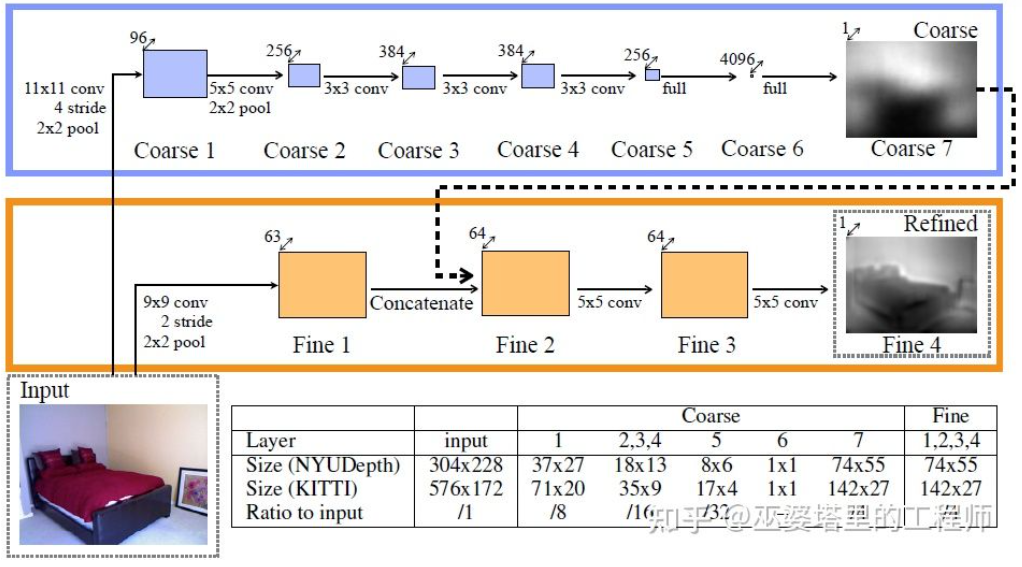
全局和局部信息融合[21]
文献[22]进一步提出采用卷积神经网络输出的多尺度特征图来预测不同分辨率的的深度图([21]中只有两种分辨率)。这些不同分辨率的特征图通过连续MRF进行融合后得到与输入图像对应的深度图。
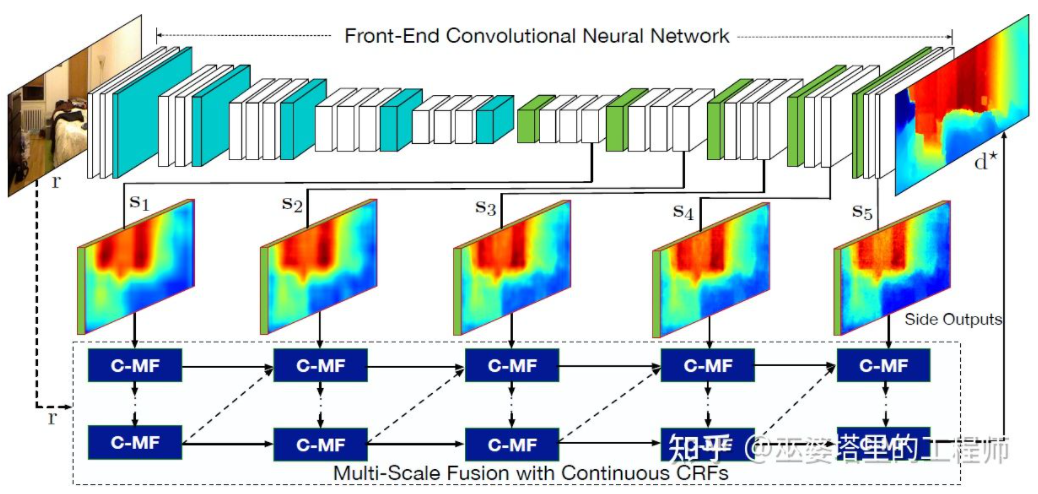
多尺度信息融合[22]
以上两篇文章都是采用卷积神经网络来回归深度图,另外一个思路是把回归问题转换为分类问题,也就是将连续的深度值划分为离散的区间,每个区间作为一个类别。这个方向的代表性工作是DORN[23]。DORN框架中的神经网络也是一个编码解码的结构,不过细节上有些差别,比如采用全连接层解码,膨胀卷积进行特征提取等。
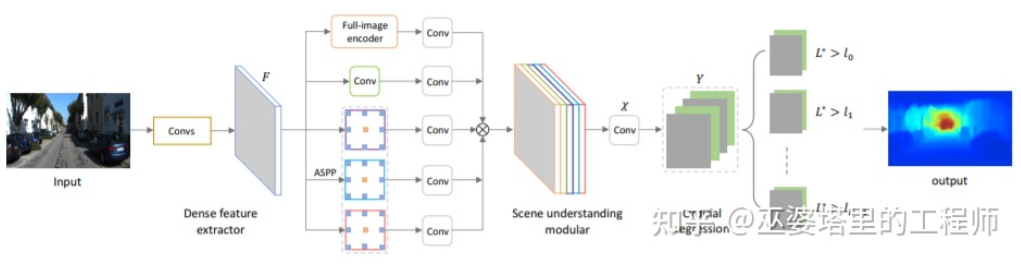
DORN深度分类
前面提到,深度估计与语义分割任务有着相似之处,因此感受野的大小对深度估计来说也是非常重要的。除了以上提到的金字塔结和膨胀卷积,最近非常流行的Transformer结构具有全局的感受野,因此也非常适合此类任务。文献[24]中就提出采用Transformer和多尺度结构来同时保证预测的局部精确性和全局一致性。
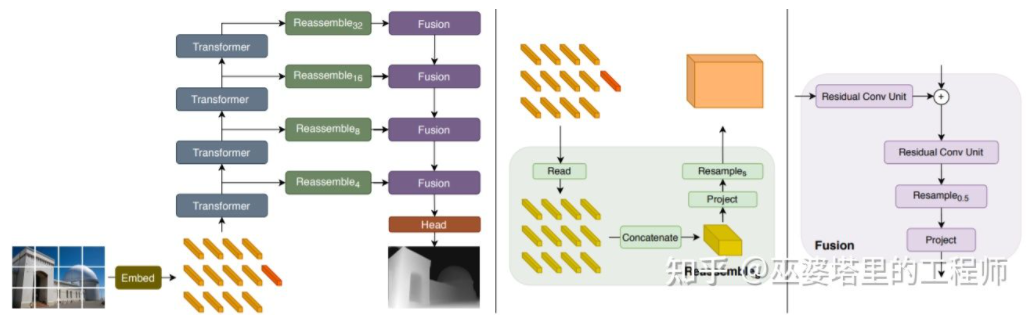
Transformer for Dense Prediction
虽然可以利用先验知识和图像中的上下文信息,基于单目的3D感知的准确度并不能完全令人满意。尤其是当采用深度学习的策略时,算法的准确度非常依赖于数据集的大小和质量。对于数据集中没有出现过的场景,算法在深度估记和物体检测上都会有较大的偏差。
双目视觉可以解决透视变换带来的歧义性,因此从理论上来说可以提高3D感知的准确度。但是双目系在硬件和软件上要求都比较高。硬件上来说需要两个精确配准的摄像头,而且需要保证在车辆运行过程中始终保持配准的正确性。软件上来说算法需要同时处理来自两个摄像头的数据,计算复杂度较高,保证算法的实时性就更加困难。
总的来说,与单目视觉感知相比,双目视觉感知的工作相对较少,下面会挑选几篇典型的文章进行介绍。此外,还有一些基于多目的工作,但是偏向于系统应用的层面,比如说特斯拉在AI Day上展示的360°感知系统。
3DOP[25]首先利用来自双摄像头的图像生成深度图,将深度图转化为点云后再将其量化为网格数据结构,并以此为输入来生成3D物体候选。生成候选时用到了一些直觉和先验的的知识,比如候选框中点云的密度足够大,高度与实际物体一致并且与框外的点云高度相差足够大,候选框与Free Space的重叠足够小。通过这些条件最终在3D空间中采样出大约2K个3D物体候选。这些候选映射到2D图像上,通过ROI Pooling进行特征提取,用来预测物体的类别和细化物体框。这里的图像输入可以是来自一个摄像头的RGB图像,或者深度图。
总的来说,这是一个两阶段的检测方法。第一阶段采用深度信息(点云)生成物体候选,第二阶段采用图像信息(或者深度)再进行细化。理论上说,第一阶段的点云生成也可以用LiDAR代替,作者也因此进行了实验对比。LiDAR的优势在于测距精确,因此对于小物体,部分遮挡的物体和远处的物体来说效果较好。双目视据的优势在于点云密度高,因此在近距离遮挡较少,物体也相对较大的情况下效果更好。当然在不考虑成本和计算复杂度的前提下,将二者融合会得到最好的效果。
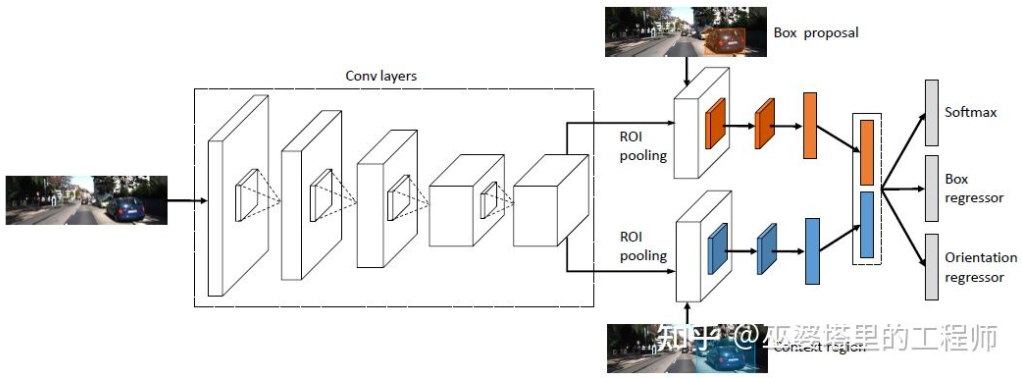
3DOP
3DOP与上一节中介绍的Pseudo-LiDAR[3]有着类似的思路,都是将稠密的深度图(来自单目,双目甚至低线数LiDAR)转换为点云,然后再应用点云物体检测领域的算法。
从图像估计深度图,再由深度图生成点云,最后再应用点云物体检测算法,这个流程的各个步骤是分开进行的,无法进行端对端的训练。DSGN[26]提出了一个单阶段的算法,从左右图像出发,通过Plane-Sweep Volume这种中间表示来生成BEV视图下的3D表示,并且同时进行深度估计和物体检测。这个流程的所有步骤都是可以求导的,因此可以进行端对端的训练。
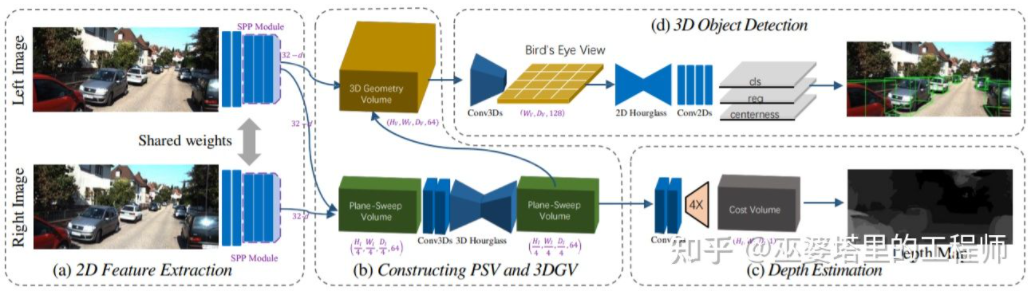
DSGN
深度图是一种稠密的表示,其实对于物体学习来说并不需要在场景的所有位置上获得深度信息,而只需要在感兴趣的物体位置进行估计就可以了。之前在介绍单目算法也提到了类似的想法。Stereo R-CNN[27]中并没有估计深度图,而是在RPN的框架下将来自两个摄像头的特征图叠放在一起来生成物体候选。这里将左右摄像头的信息关联在一起的关键在于标注数据的变化。如下图所示,除了左右两个标注框,还增加了左右两个标注框的Union。与左右任意一个框IoU超过0.7的Anchor作为Positive样本,与Union框IoU小于0.3的Anchor作为Negative样本。Positive的Anchor会同时回归左右标注框的位置和大小。除了物体框,该方法还采用了角点作为辅助。有了所有这些信息后就可以恢复3D物体框。
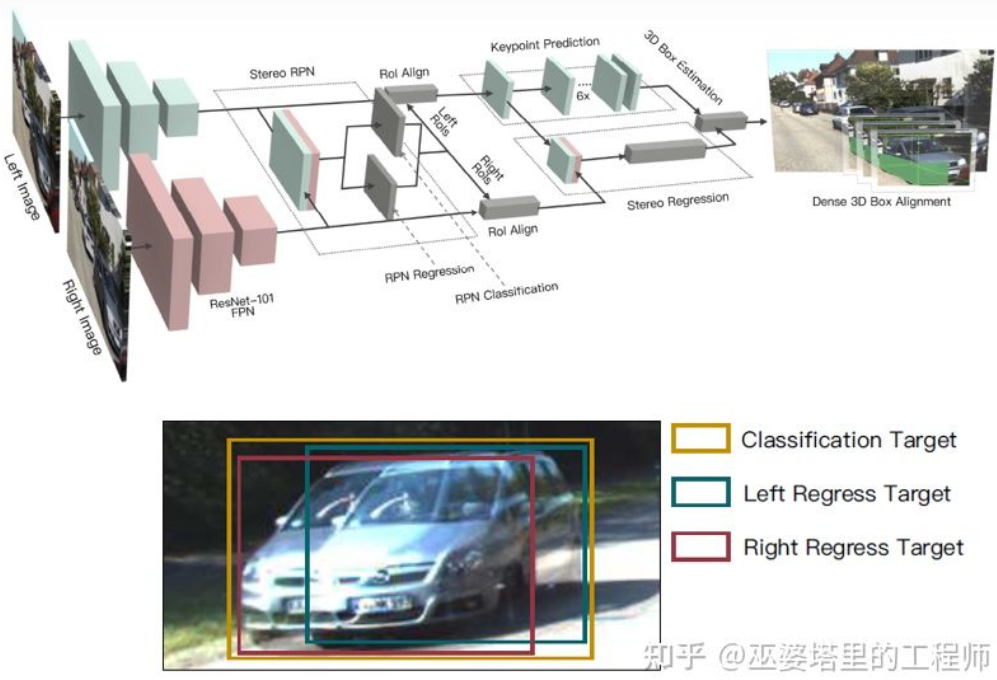
Stereo R-CNN
对整个场景进行稠密的深度估计,甚至会对物体检测带来不好的影响。比如物体边缘由于与背景重叠导致深度估计偏差较大,整个场景深度范围很大也会影响算法的速度。因此,与Stereo RCNN类似,文献[28]中也提出只在感兴趣的物体处估计深度,并且只生成物体上的点云。这些以物体为中心的点云最后被用来预测物体的3D信息。
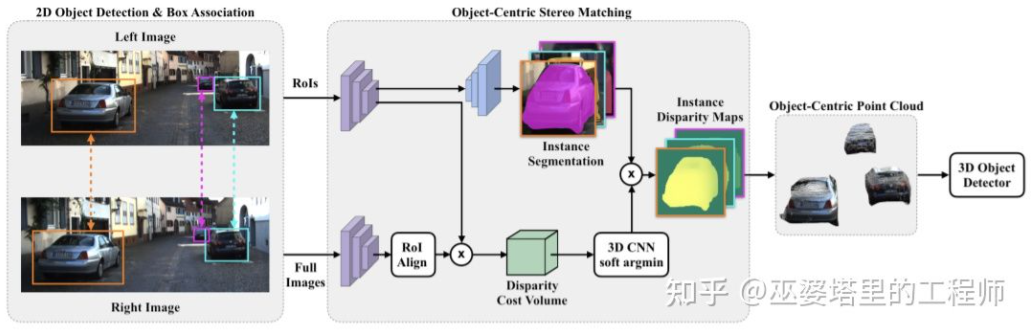
Object-Centric Stereo Matching
与单目感知算法类似,深度估计在双目感知中也是关键的步骤。从上一小节对双目物体检测的介绍来看,很多算法都采用了深度估计,包括场景级的深度估计和物体级的深度估计。下面就简单回顾一下双目深度估计的基本原理和几个代表性的工作。
双目深度估计的原理其实也很简单,就是根据左右两张图像上同一个3D点之间的距离d(假设两个相机保持同一高度,因此只考虑水平方向的距离),相机的焦距f,以及两个相机之间的距离B(基线长度),来估计3D点的深度。
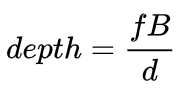
在双目系统中,f和B是固定的,因此只需要估计距离d,也就是视差。对于每个像素点来说,需要做的就是找到另一张图像中匹配的点。距离d的范围是有限的,因此匹配的搜索范围也是有限的。对于每一个可能的d,都可以计算每个像素点处的匹配误差,因此就得到了一个三维的误差数据,称之为Cost Volume。在计算匹配误差时,一般都会考虑像素点附近的局部区域,一个最简单的方法就是对局部区域内所有对应像素值的差进行求和:
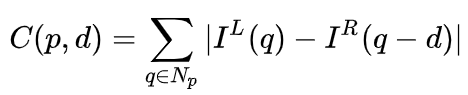

MC-CNN[29]把匹配过程形式化为计算两个图像块的相似度,并且通过神经网络来学习图像块的特征。通过标注数据,可以构建一个训练集。在每个像素点处,都生成一个正样本和负样本,每个样本都是一对图像块。其中正样本是来自同一个3D点的两个图像块(深度相同),负样本则是来自不同3D点的图像块(深度不同)。负样本的选择有很多,为了保持正负样本的平衡,只随机采样一个。有了正负样本,就可以训练神经网络来预测相似度。这里的核心思想其实就是通过监督信号来指导神经网络学习适用于匹配任务的图像特征。
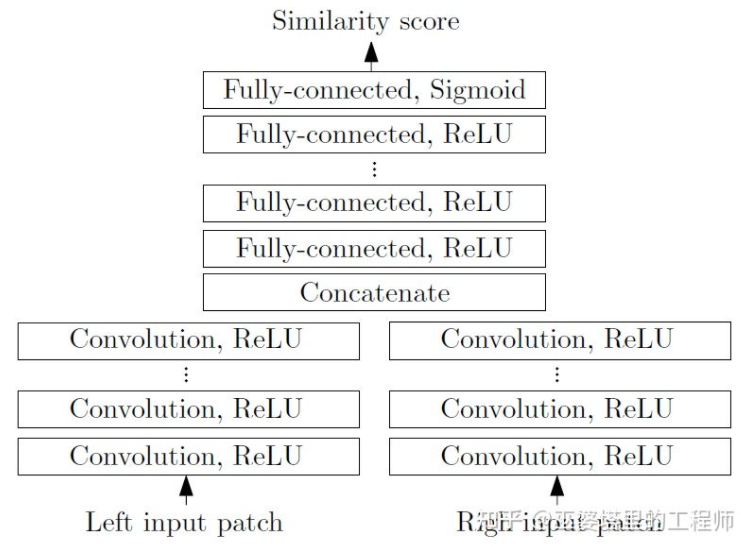
MC-CNN
MC-Net主要有两点不足:1)Cost Volumn的计算依赖于局部图像块,这在一些纹理较少或者模式重复出现的区域会带来较大的误差;2)后处理的步骤依赖于手工设计,需要花费大量时间,也很难保证最优。GC-Net[30]针对这两点进行了改进。首先,在左右图像上进行多层卷积和下采样操作,以更好的提取语义特征。对于每一个视差级别(以像素为单位),将左右特征图进行对齐(像素偏移)后再进行拼接,就得到了该视差级别的特征图。所有视差级别的特征图合并在一起,就得到了4D的Cost Volumn(高度,宽度,视差,特征)。Cost Volumn只包含了来自单个图像的信息,图像之间并没有交互。因此,下一个步骤是采用3D卷积处理Cost Volumn,这样可以同时提取左右图像之间的相关信息以及不同视差级别之间的信息。这一步的输出是3D的Cost Volumn(高度,宽度,视差)。最后,我们需要在视差这个维度上求Argmin,以得到最优的视差值,但是标准的Argmin是无法求导的。GC-Net中采用Soft Argmin,解决的求导的问题,从而使整个网络可以进行端对端的训练。
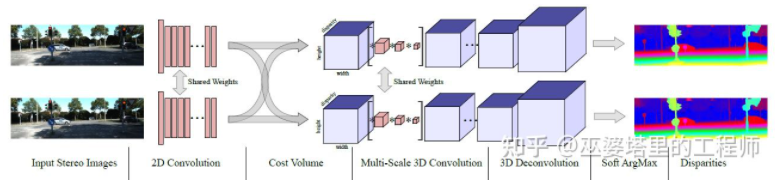
GC-Net
PSMNet[31]与GC-Net的结构非常相似,但是在两个方面进行了改进:1)采用金字塔结构和空洞卷积来提取多分辨率的信息并且扩大感受野。得益于全局和局部特征的融合,Cost Volumn的估计也更加准确。2)采用多个叠加的Hour-Glass结构来增强3D卷积。全局信息的利用被更进一步强化了。总的来说,PSMNet在全局信息的利用上做了改进,从而使视差的估计更多依赖于不同尺度的上下文信息而不是像素级别的局部信息。
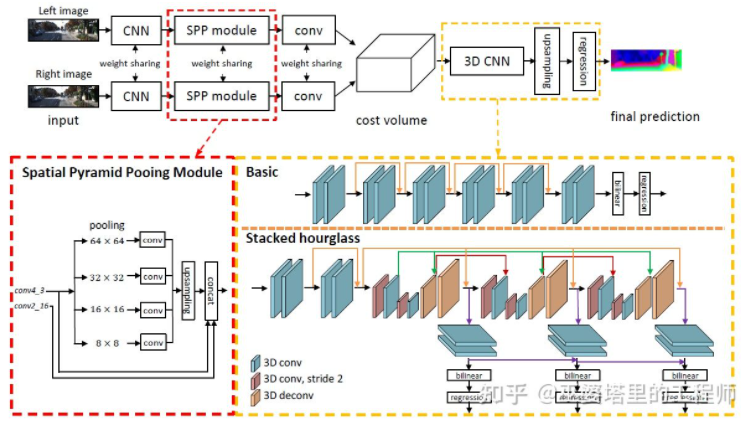
PSMNet
Cost Volumn中的,视差级别是离散的(以像素为单位),神经网络所学习的是在这些离散点上的Cost分布,而分布的极值点就对应了当前位置的视差值。但是视差(深度)值其实应该是连续的,用离散的点来估计会带来误差。CDN[32]中提出了连续估计的概念,除了离散点的分布以外,还估记了每个点处的偏移。离散点和偏移量一起,就构成了连续的视差估计。
CDN
参考文献
[1] Kim et al., Deep Learning based Vehicle Position and Orientation Estimation via Inverse Perspective Mapping Image, IV 2019.
[2] Roddick et al., Orthographic Feature Transform for Monocular 3D Object Detection, BMVC 2019.
[3] Wang et al., Pseudo-LiDAR from Visual Depth Estimation: Bridging the Gap in 3D Object Detection for Autonomous Driving, CVPR 2019.
[4] You et al., Pseudo-LiDAR++: Accurate Depth for 3D Object Detection in Autonomous Driving, ICLR 2020.
[5] Weng and Kitani, Monocular 3D Object Detection with Pseudo-LiDAR Point Cloud, ICCV 2019.
[6] Vianney et al., RefinedMPL: Refined Monocular PseudoLiDAR for 3D Object Detection in Autonomous Driving, 2019.
[7] Chabot et al., Deep MANTA: A Coarse-to-fine Many-Task Network For Joint 2D and 3D Vehicle Analysis From Monocular Image, CVPR 2017.
[8] Kundu et al., 3D-RCNN: Instance-level 3D Object Reconstruction via Render-and-Compare, CVPR 2018.
[9] Qin et al., MonoGRNet: A Geometric Reasoning Network for Monocular 3D Object Localization, AAAI 2019.
[10] Barabanau et al., Monocular 3D Object Detection via Geometric Reasoning on Keypoints, 2019.
[11] Bertoni et al., MonoLoco: Monocular 3D Pedestrian Localization and Uncertainty Estimation, ICCV 2019.
[12] Mousavian et al., 3D Bounding Box Estimation Using Deep Learning and Geometry, CVPR 2016.
[13] Naiden et al., Shift R-CNN: Deep Monocular 3D Object Detection with Closed-Form Geometric Constraints, ICIP 2019.
[14] Choi et al., Multi-View Reprojection Architecture for Orientation Estimation, ICCV 2019.
[15] Chen et al., Monocular 3D Object Detection for Autonomous Driving, CVPR 2016.
[16] Brazil and Liu, M3D-RPN: Monocular 3D Region Proposal Network for Object Detection, ICCV 2019.
[17] Qin et al., Triangulation Learning Network: from Monocular to Stereo 3D Object Detection, CVPR 2019.
[18] Jörgensen et al., Monocular 3D Object Detection and Box Fitting Trained End-to-End Using Intersection-over-Union Loss, 2019.
[19] Wang et al., FCOS3D: Fully Convolutional One-Stage Monocular 3D Object Detection, 2021.
[20] Liu et al., SMOKE: Single-Stage Monocular 3D Object Detection via Keypoint Estimation, CVPRW 2020.
[21] Eigen, et al.,Depth Map Prediction from a Single Image using a Multi-Scale Deep Network, NIPS 2014.
[22] Xu et al., Monocular Depth Estimation using Multi-Scale Continuous CRFs as Sequential Deep Networks, TPAMI 2018.
[23] Fu et al., Deep Ordinal Regression Network for Monocular Depth Estimation, CVPR 2018.
[24] Ranftl et al., Vision Transformers for Dense Prediction, ICCV 2021.
[25] Chen et al., 3D Object Proposals using Stereo Imagery for Accurate Object Class Detection, TPAMI 2017.
[26] Chen et al., DSGN: Deep Stereo Geometry Network for 3D Object Detection, CVPR 2020.
[27] Li et al., Stereo R-CNN based 3D Object Detection for Autonomous Driving, CVPR 2019.
[28] Aon et al., Object-Centric Stereo Matching for 3D Object Detection, CVPR 2020.
[29] Zbontar and LeCun. Stereo matching by training a convolutional neural network to compare image patches, JMLR 2016.
[30] Kendall, et al., End-to-end learning of geometry and context for deep stereo regression, ICCV 2017.
[31] Chang and Chen et al., Pyramid Stereo Matching Network, 2018.
[32] Garg et al., Wasserstein Distances for Stereo Disparity Estimation, NeurIPS, 2020.
转载自知乎@巫婆塔里的工程师,文中观点仅供分享交流,不代表本公众号立场,如涉及版权等问题,请您告知,我们将及时处理。
-- END --