↑点击上方蓝色字体,关注“嵌入式软件实战派”获得更多精品干货。
循环冗余校验(英语:Cyclic redundancy check,通称“CRC”)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数,主要用来检测或校验数据传输或者保存后可能出现的错误。
Wikipedia
一句话:CRC是将数据计算出散列的方式,一般用于校验数据的完整性。它具有简单、执行效率高等特点。当然,你可以类比于Checksum,但比Checksum复杂些,防碰撞性更好些。

整个运算过程是这样的:
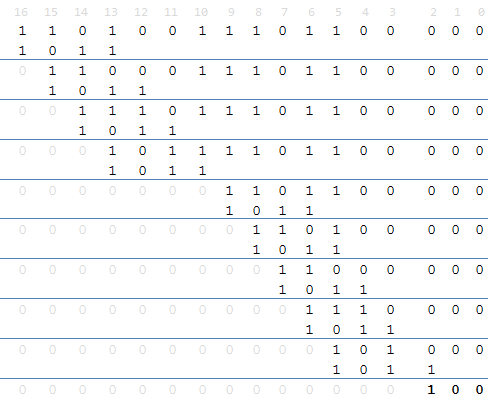
实际上就是逐个bit移位做异或。
详见:https://en.wikipedia.org/wiki/Cyclic_redundancy_check
实际上,人们根据不同的需要,做了很多种计算方式,主要差别在于CRC长度、多项式、初始值、结果是否需要异或、是否需要翻转等等。
首先,来看看几个概念:
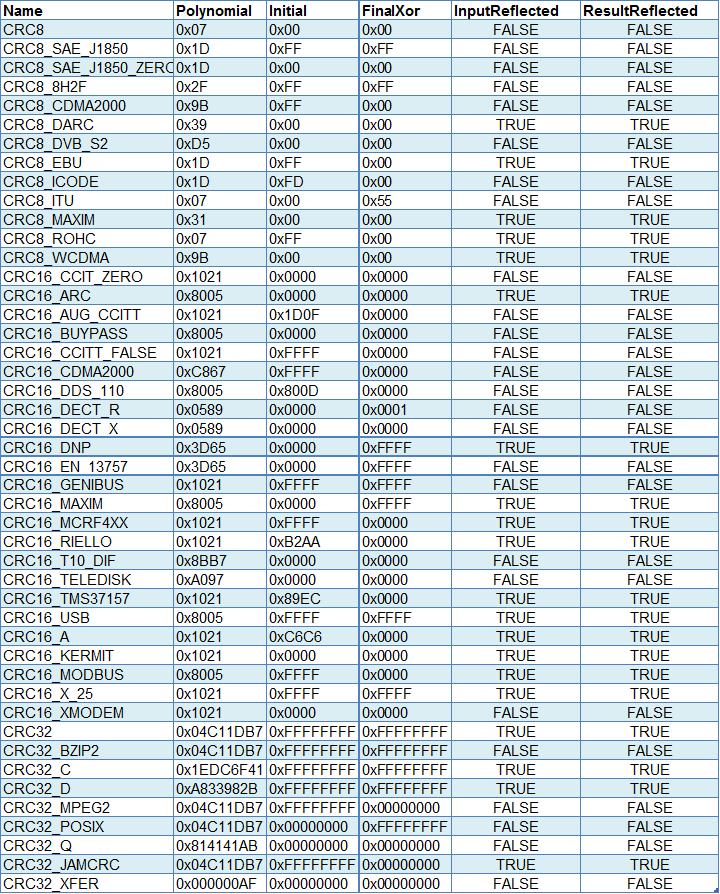
从上面的CRC名称可以看出,不同的算法是有不同用途的,这是国际常规的用法定义,其实如果是用户自己用也没特别要求,可以自由点。
#define CRC_POLYNOMIAL_8 0x0Cuint8 crc_8(uint8 crc, uint8* pdata, uint32 len){for (uint32 i = 0; i < len; i++){crc ^= pdata[i];for (uint8 j = 0; j < 8; j++){if ((crc & 0x80u) > 0){crc = ( (uint8)(crc << 1u) ) ^ CRC_POLYNOMIAL_8;}else{crc <<= 1u;}}}return crc;}
2.1 多项式生成的表
在开始这个话题之前,我们得回个头来看看那几个概念中有个InputReflected和OutputReflected。干啥呢,吃饱没事干啊,算就算,还要翻转?呵呵!
其实,通过多项式生成表就可以生成正序和逆序,就是为了应付这个“翻转”的。举个例子以CRC8_ITU(Polynomial=0x07)看看这个表:
正序表为
const unsigned char crc8_itu__table[] ={0x00, 0x07, 0x0E, 0x09, 0x1C, 0x1B, 0x12, 0x15, 0x38, 0x3F, 0x36, 0x31, 0x24, 0x23, 0x2A, 0x2D,0x70, 0x77, 0x7E, 0x79, 0x6C, 0x6B, 0x62, 0x65, 0x48, 0x4F, 0x46, 0x41, 0x54, 0x53, 0x5A, 0x5D,// ...... 省略部分0xAE, 0xA9, 0xA0, 0xA7, 0xB2, 0xB5, 0xBC, 0xBB, 0x96, 0x91, 0x98, 0x9F, 0x8A, 0x8D, 0x84, 0x83,0xDE, 0xD9, 0xD0, 0xD7, 0xC2, 0xC5, 0xCC, 0xCB, 0xE6, 0xE1, 0xE8, 0xEF, 0xFA, 0xFD, 0xF4, 0xF3,};
逆序表为
const unsigned char crc8_itu_reversed_table[] ={0x00, 0x91, 0xE3, 0x72, 0x07, 0x96, 0xE4, 0x75, 0x0E, 0x9F, 0xED, 0x7C, 0x09, 0x98, 0xEA, 0x7B,0x1C, 0x8D, 0xFF, 0x6E, 0x1B, 0x8A, 0xF8, 0x69, 0x12, 0x83, 0xF1, 0x60, 0x15, 0x84, 0xF6, 0x67,// ...... 省略部分0xA8, 0x39, 0x4B, 0xDA, 0xAF, 0x3E, 0x4C, 0xDD, 0xA6, 0x37, 0x45, 0xD4, 0xA1, 0x30, 0x42, 0xD3,0xB4, 0x25, 0x57, 0xC6, 0xB3, 0x22, 0x50, 0xC1, 0xBA, 0x2B, 0x59, 0xC8, 0xBD, 0x2C, 0x5E, 0xCF,};
2.2 通用查表法
网上有很多种查表发计算CRC,不尽相同。于是我做了个通用版,满足各种算法,其中用了宏定义的奇技淫巧。直接上代码:
uintuintBOOL inputReflected, BOOL resultReflected) \{ \uintuintconst uintfor(int i = 0; i < len; i++) \{ \uintif(inputReflected) \{ \curByte = Reflect8(pdata[i]); \} \/* update the MSB of crc value with next input byte */ \temp1 = (crc ^ (curByte << (width - 8))); \/* this MSB byte value is the index into the lookup table */ \pos = (temp1 >> (width - 8)) & 0xFF; \/* shift out this index */ \temp2 = (temp1 << 8); \/* XOR-in remainder from lookup table using the calculated index */ \crc = (temp2 ^ pTable[pos]); \} \if(resultReflected) \{ \crc = Reflect} \return (crc ^ finalXor); \}
怎么用?
先定义,即定义对于位数算法的函数,通过预编译生成:
DEF_CRC_FUNC(gen_crc8, 8, crc8__table);DEF_CRC_FUNC(gen_crc16_maxim, 16, crc16_maxim__table);DEF_CRC_FUNC(gen_crc16_a, 16, crc16_a__table);DEF_CRC_FUNC(gen_crc32_jamcrc, 32, crc32_jamcrc__table);
再调用,测试可以在main函数调用:
int main(void){const uint8 buf[6] = "123456";uint8 crc8 = gen_crc8(buf, 6, 0x00, 0x00, 0, 0);uint16 crc16_maxim = gen_crc16_maxim(buf, 6, 0x0000, 0xFFFF, 1, 1);uint16 crc16_a = gen_crc16_a(buf, 6, 0xC6C6, 0x0000, 1, 1);uint32 crc32_jamcrc = gen_crc32_jamcrc(buf, 6, 0xFFFFFFFF, 0x00000000, 1, 1);printf("crc8: %X\n", crc8);printf("crc16_maxim: %X\n", crc16_maxim);printf("crc16_a: %X\n", crc16_a);printf("crc32_jamcrc: %X\n", crc32_jamcrc);}
这里还是有个问题,就那个“翻转”的问题,每个byte都做翻转,很浪费CPU资源啊。作为“优秀的”嵌入式软件开发人员,我们是追求卓越的算法,于是乎,就有了以下方式:
(1)对于InputReflected和OutputReflected都是False的,我们用正序表,以CRC8_ITU为例:
/*CRC Info:Name Polynomial Initial FinalXor InputReflected ResultReflectedCRC8_ITU 0x07 0x00 0x55 false false*/unsigned char crc8_itu(unsigned char crc, const unsigned char* buf, unsigned int len){for(unsigned int i = 0; i < len; i++){crc = crc8_itu__table[crc ^ buf[i]];}return crc^0x55;}
(2)对于InputReflected和OutputReflected都是True的,我们用逆序表,以CRC8_EBU为例:
/*CRC Info:Name Polynomial Initial FinalXor InputReflected ResultReflectedCRC8_EBU 0x1D 0xFF 0x00 true true*/unsigned int crc8_ebu(unsigned int crc, const unsigned char* buf, unsigned int len){int i = 0; i < len; i++){crc = crc8_ebu_reversed_table[crc ^ buf[i]];}return crc^0x00;}
说了这么多,以上都是举例而已(其实直接将上面代码copy过去验证也是木有问题的,不要怀疑),上代码啊
Talk is cheap. Show me the code.
Linus Torvalds
我将上面表格中提到的所有CRC算法,都coding了,就像下图的这些
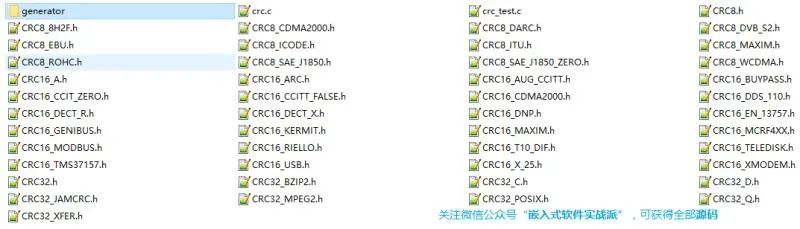
举个例子,CRC32_BZIP2.h文件是的算法是这样的:
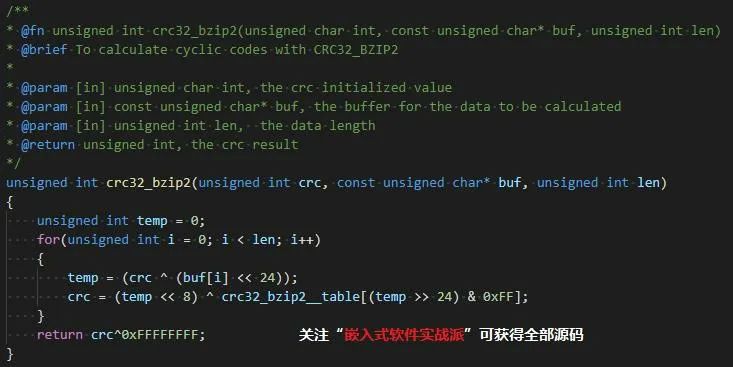
// TEST:Caculate the string "123456", result list below with different crc models:crc_assert(0xfd == crc8 (0x00, "123456", 6), "crc8" );// ...... 省略部分crc_assert(0x57 == crc8_rohc (0xFF, "123456", 6), "crc8_rohc" );crc_assert(0xab == crc8_wcdma (0x00, "123456", 6), "crc8_wcdma" );crc_assert(0x20e4 == crc16_ccit_zero (0x0000, "123456", 6), "crc16_ccit_zero" );crc_assert(0x29e4 == crc16_arc (0x0000, "123456", 6), "crc16_arc" );// ...... 省略部分crc_assert(0x32e4 == crc16_modbus (0xFFFF, "123456", 6), "crc16_modbus" );crc_assert(0xe672 == crc16_x_25 (0xFFFF, "123456", 6), "crc16_x_25" );crc_assert(0x20e4 == crc16_xmodem (0x0000, "123456", 6), "crc16_xmodem" );crc_assert(0x0972d361 == crc32 (0xFFFFFFFF, "123456", 6), "crc32" );// ...... 省略部分crc_assert(0xf036f1c2 == crc32_xfer (0x00000000, "123456", 6), "crc32_xfer" );

往期精彩内容推荐>>>
我在马路上遇到一个死锁问题
我硬生生地把C代码塞进了Python和Ruby
C语言的奇技淫巧之四
SREC、Hex、Bin等烧录文件格式完全解读