
(1)
利用 z 变换的变换域中的微分性质:

因此,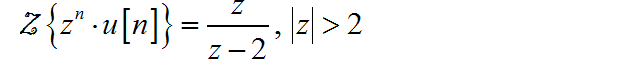
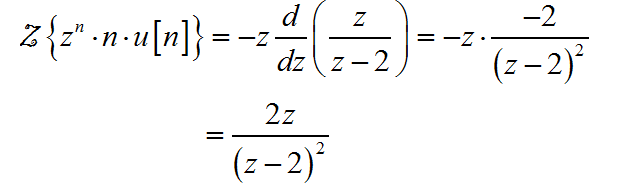
(2)
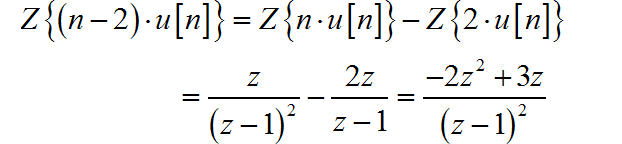
(3)
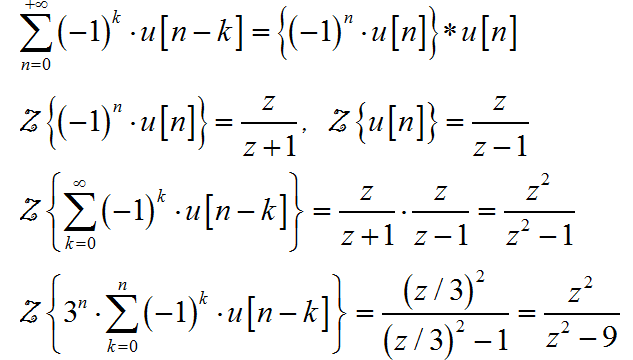
(4)
首先有:
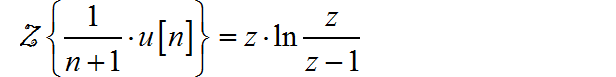
那么, 根据 z 变换的位移定理:
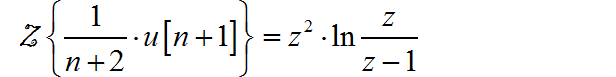
在根据 z 变换的指数加权特性:

另外一种求解方法:
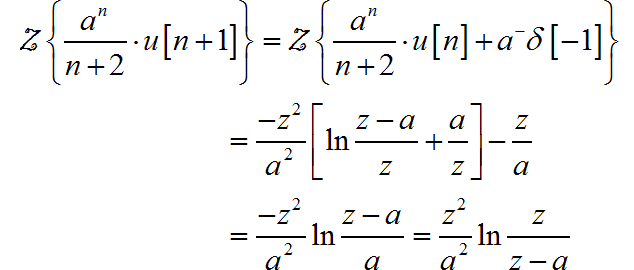
(5)

(1)
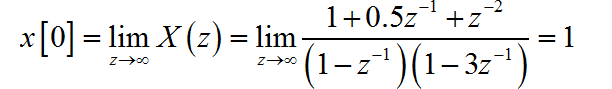
由于 存在一个位于单位圆外的极点 ,所以序列的终值不存在。
(2)

(3)
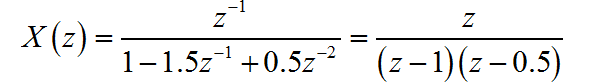
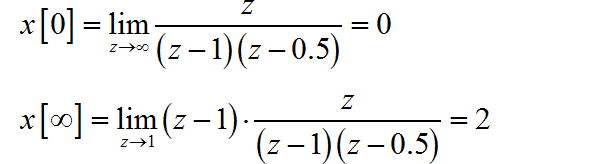
(4)
这是一个假分式, 通过长除方法将其展成 z 的多项式和真分式。
其中常量项对应序列的初值, 即: 。
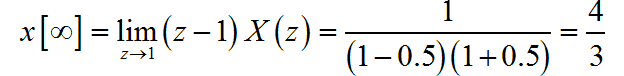
(1)
根据 z 变换的卷积定理, , 那么 的 z 变换为:
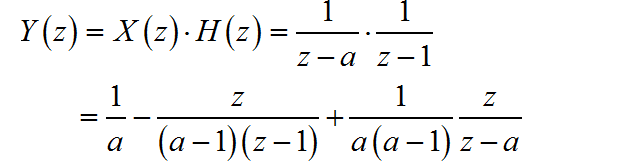 所以
所以
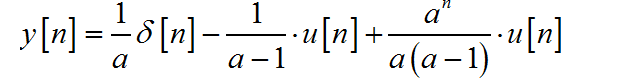
(2)
序列 的 z 变换分别为:
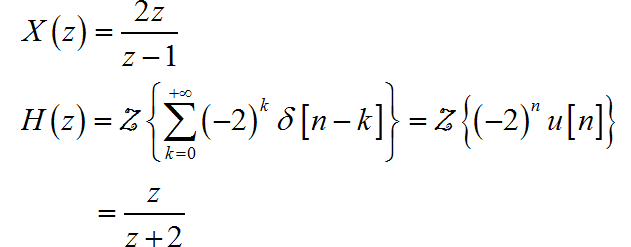
根据 z 变换的卷积定理,可以知道:
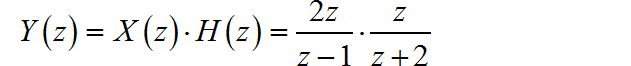
进行因式分解,可得:
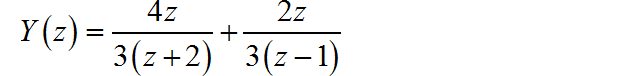 所以:
所以:

(1)
根据 z 变换时域乘积定理,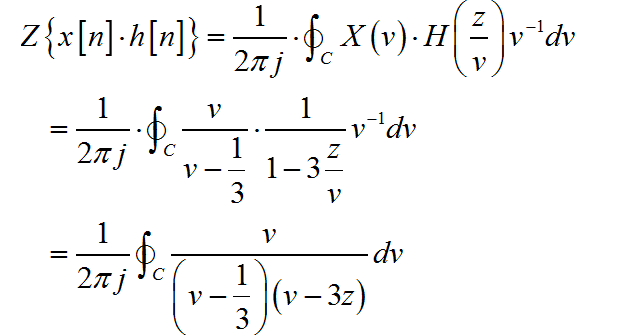
根据 的收敛域, 可知 , 根据 的收敛域,可知 ,即 。所以 在上述围线积分中, 包括有两个极点分别是 。利用留数定理计算上述围线积分:

由此,可以知道 。
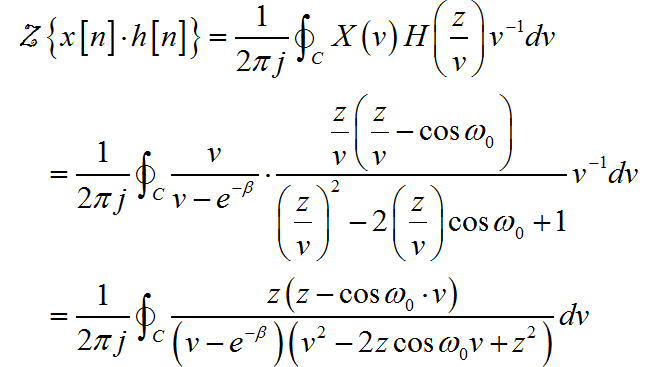
根据 的收敛域,可知:$\left| v \right| > e{ - \beta } ,\left| v \right| < \left| z \right|围
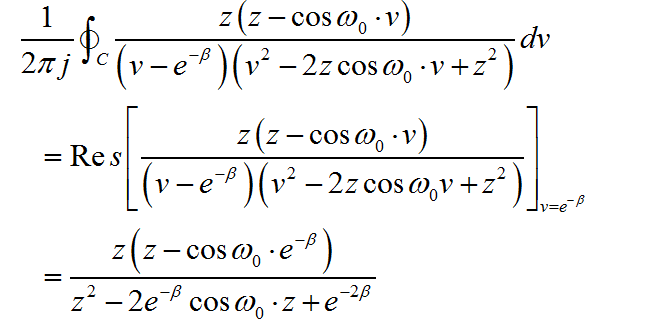
对照典型信号 z 变换表格,可知: 。
序列的累加,可以看成序列 与 的卷积, 即:
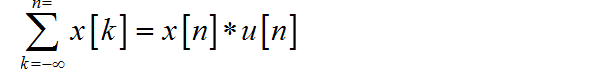
根据 z 变换的卷积定理,可知序累加和的 在变换等于序列的z变换乘以 的 z 变换。由于:
所以:
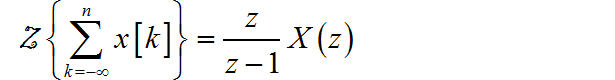
(1)
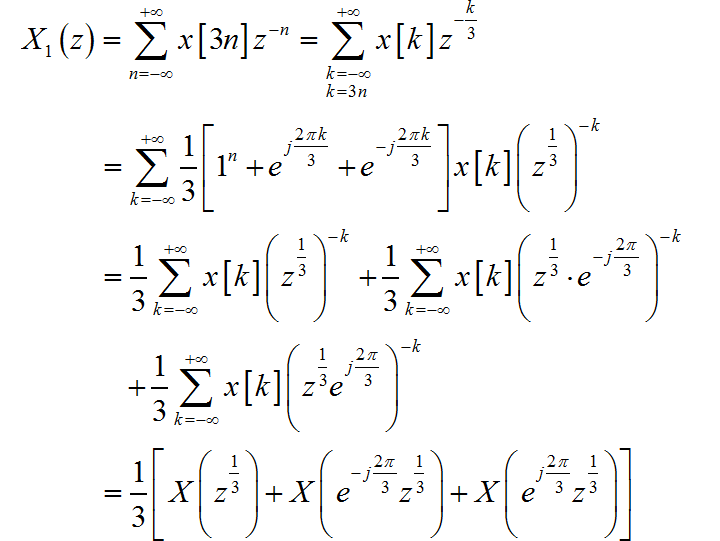
(2)
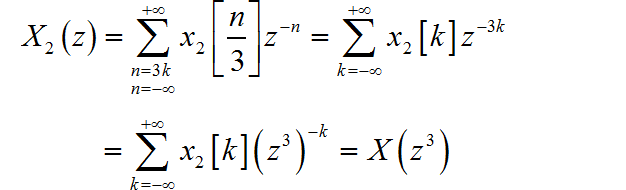
(1)
对微分方程两边进行 Laplace 变换, 利用 Laplace 变换微分定理可以将系统的初始条件代入方程:

利用 因式分解方法,求解 y(s):

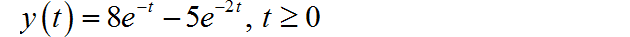
(2)
对微分方程两边进行 Laplace 变换:

利用因式分解方法,求解微分方程时域表达式:
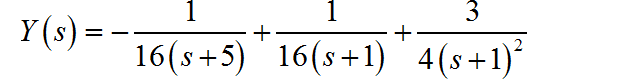
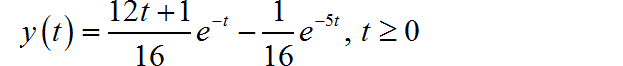
(1)
对差分方程左右同时求 z 变换。
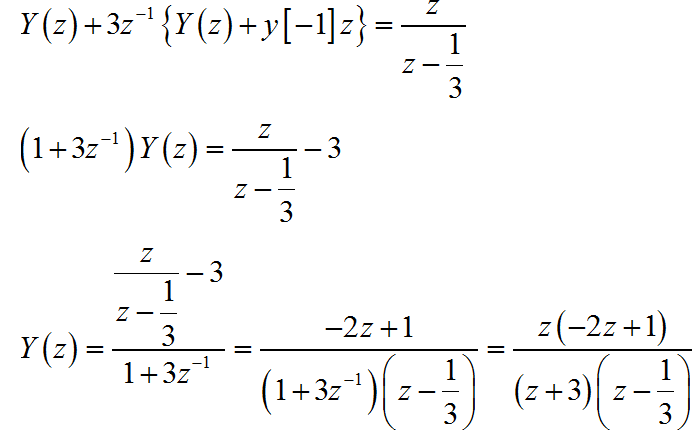
对 Y(z) 进行因式分解:
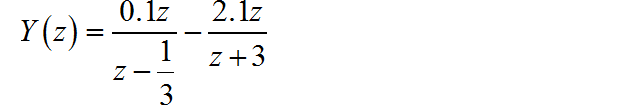
对应的右边序列为:
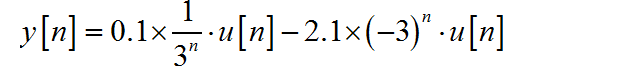
(2)
对差分方程左右同时求 z 变换:
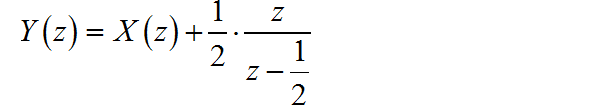
进行 z 反变换,可得:
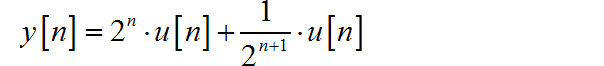
系统的单位冲激响应的 Laplace 变换对应系统函数。
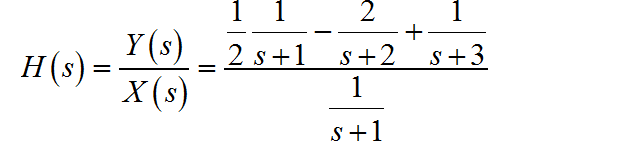
进行化简后, 因式分解:
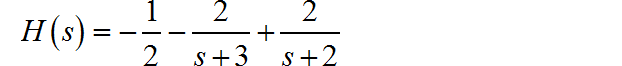
对应系统的单位冲激响应为:
(1)
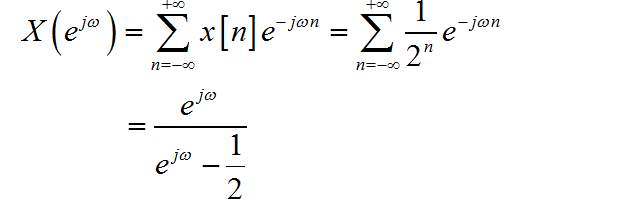
(2)
序列的 z 变换为:

那么对应序列的傅里叶变换为:
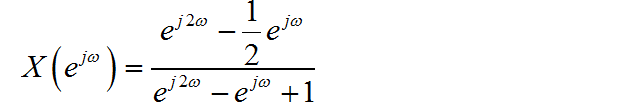
(3)

信号与系统 2023年春季作业要求与参考答案汇总: https://blog.csdn.net/zhuoqingjoking97298/article/details/130018064?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22130018064%22%2C%22source%22%3A%22zhuoqingjoking97298%22%7D
[2]信号与系统 2023(春季) 作业要求 - 第十一次次作业: https://zhuoqing.blog.csdn.net/article/details/130619855
WiFi网络不通
老师好!!我家的wifo网络突然出现问题,无法提交我用手机发给您,不好意思打扰您。

回复:(1) 请把作业提交给助教吧, 在提交信息的时候, 在信件中把自己的姓名,班级和学号标注清楚。助教信息在网络学堂中有;(2)如果无法提交,可以在下次作业中补交窗口提交, 只要在作业中另外附带一些选做题即可。
