
(1)
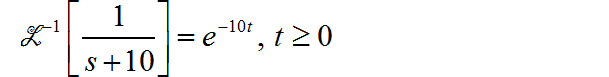
(2)
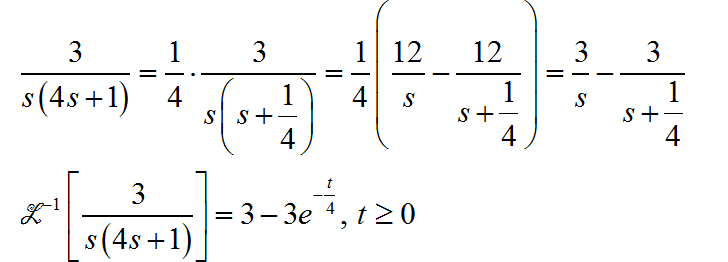
(3)
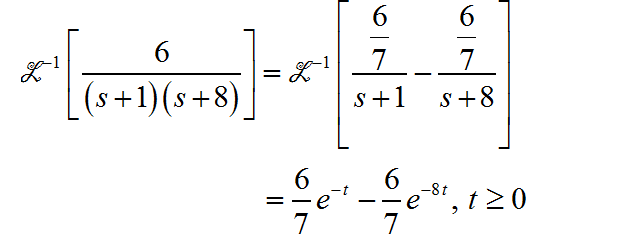
(4)
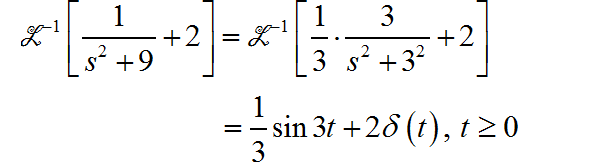
(5)
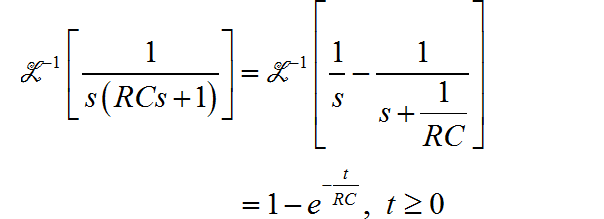
(6)
在这里先给出答案,反变换结果如下:
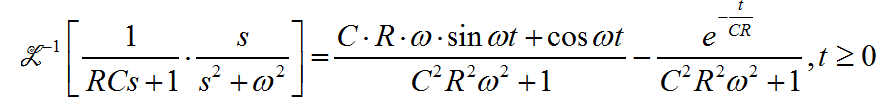
上面的答案,是利用了 Python Laplace 反变换给出的结果。下面给出手工求解过程。利用因式分解 方法进行 Laplace 反变换。根据给定的 Laplace 变换的分母多项式来看, 它存在一阶和二阶多项式, 所以可以将其分解成一阶有理分式和二阶有理分式的相加。下面给出带有待定系数的分解结果:
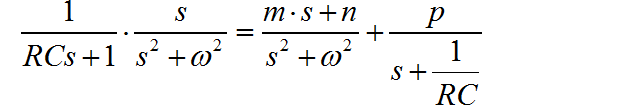
其中包括有 三个待定系数。下面将上述方程右边进行合并,
然后对比左右两个表达式分子多项式, 利用多项式系数匹配方法,求解 。
求解可得: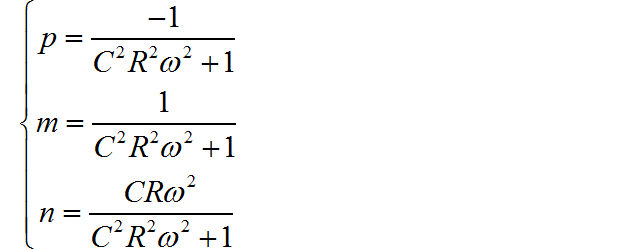
因此,因式分解后的表达式为:
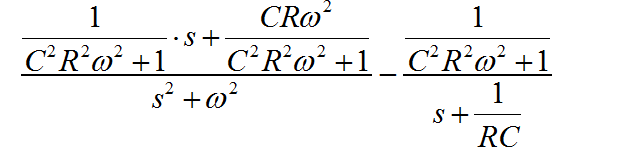
对照常用信号 Laplace 变换表格中的 指数、正弦、余弦信号的 Laplace 变换结果, 便可以写出对应的时域信号了。
(7)
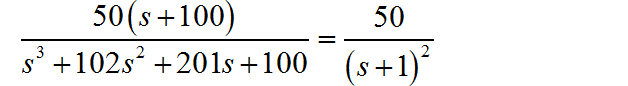

(1)
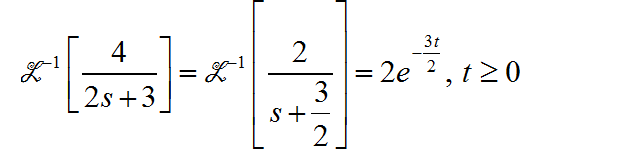
(2)
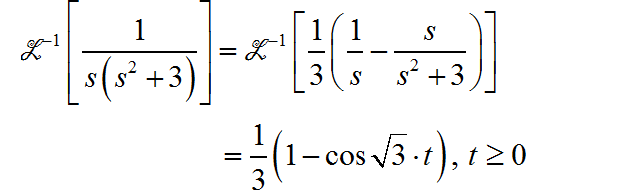
(3)
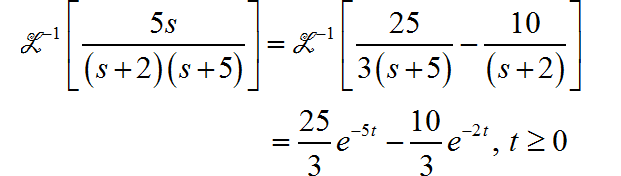
(4)
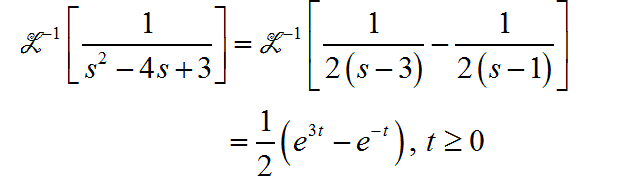
(5)

(7)
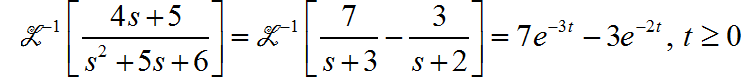
(8)
对于 Laplace 变换表达式进行因式分解:

所以,对应的 Laplace 反变换结果为:

(9)
根据 Laplace 变换公式:

两边同时对于 s 求导:
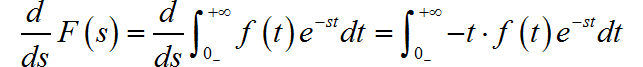
于是,得到 Laplace 变换 s 域 微分性质:
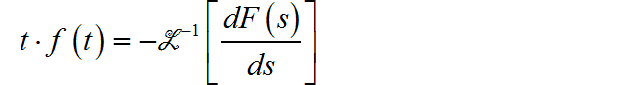
对于本小题,

根据前面得到的 Laplace 变换 s 域微分性质:
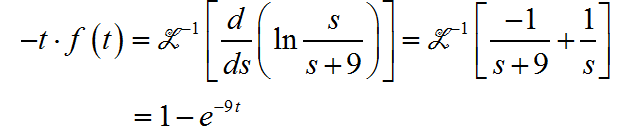 所以:
所以:

对应的 MATLAB 求解命令如下:
(1)

(2)

(3)

(4)
根据 z 变换的收敛域, 对应的序列为 左边序列:
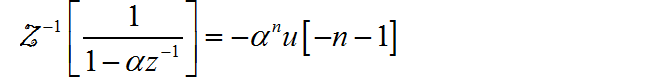
(5)
根据 z 变换的收敛域, 对应的序列为右边序列:

(6)
对表达式进行因式分解:
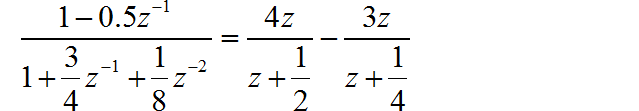
然后根据 z 变换的收敛域,写出对应的序列的表达式:
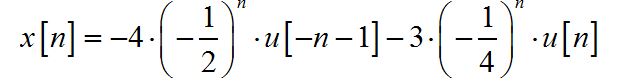
(7)
对于表达式进行 因式分解:
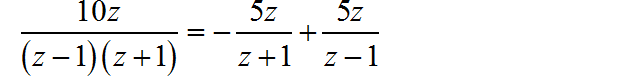
根据 z 变换的收敛域,写出对应的右边序列的表达式:

(1)
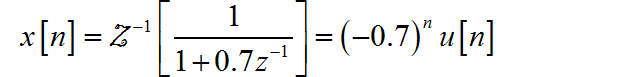
(2)
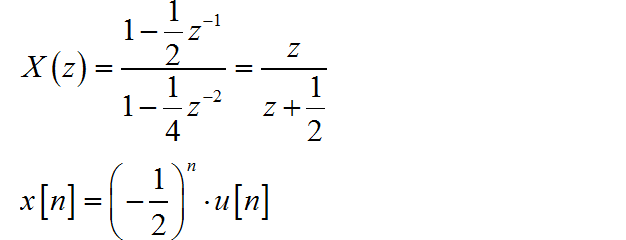
(3)


(4)
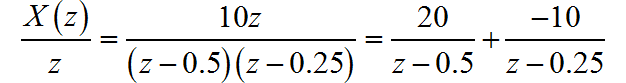
根据 z 变换的收敛域判断序列为右边序列,写出时域序列表达式:
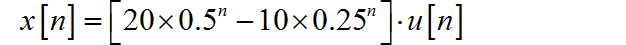
(5)
根据正弦、余弦单边序列的 z 变换公式:
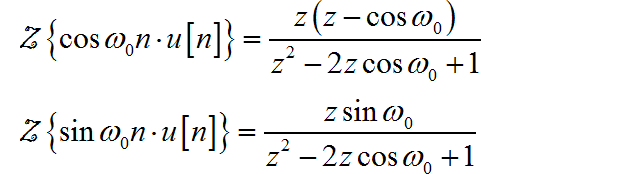
将 分别成对应的有理分式:

写出对应的右边序列的表达式:

利用三种方法求解下面的 的逆变换 :
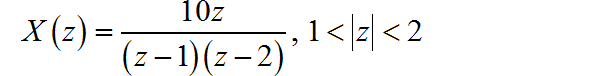
根据 z 变换的收敛域 可知序列为双边序列。在收敛域内设置逆时针围线积分路径。根据 z 反变换公式,在 时, 围线积分内只有 一阶极点。
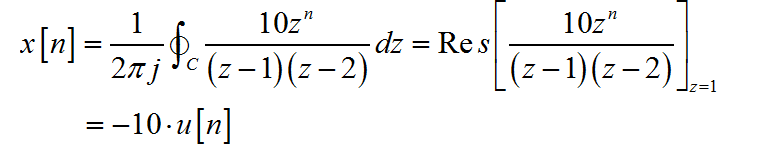
当 时,在围线积分内包括有 的一阶极点以及 处的高阶极点。在围线积分之外,只有 一阶极点。所以
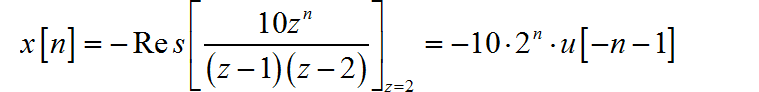
综上所述,可得:
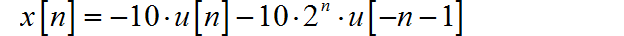
对 z 变换进行因式分解:
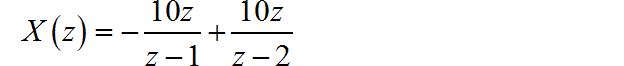
根据 z 变换的收敛域, 分别写出上面两个分解因式对应的时域序列:
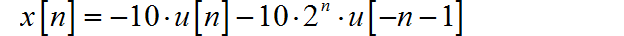
长除方法适合于单边序列。由于本题中 z 变换收敛域为一个圆环,所以需要将表达式进行因式分解,分别对左边序列和 右边序列分别使用长除方法获得序列的表达式。从这一点来看, 本题的长除方法与前面的因式分解方法很像。
对于右边序列因式使用长除方法进行展开: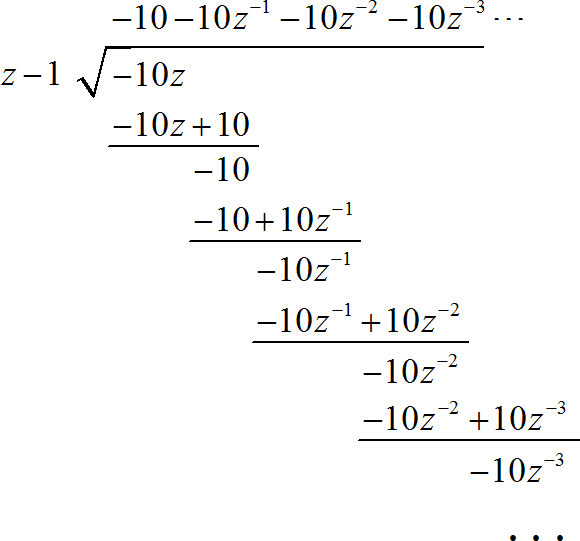
归纳出序列右边序列的表达式: 。
对于左边序列使用长除方法进行展开:
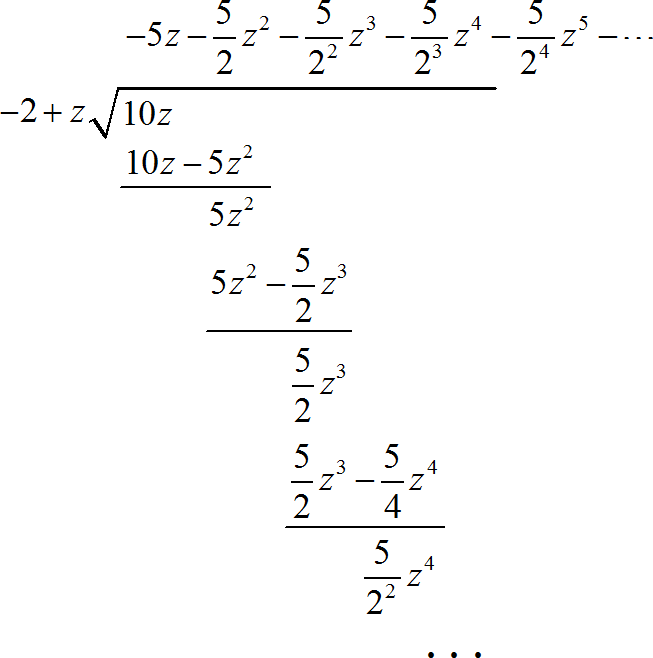
归纳出序列左侧序列的表达式: 。
合并以上两步的结论,可以得到:
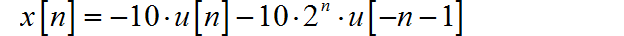
(1) 利用 Laplace 变换 s 域微分性质
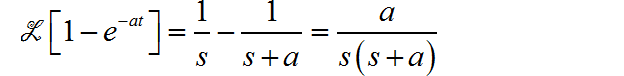

(2) 利用 Laplace 变换 s 域平移性质
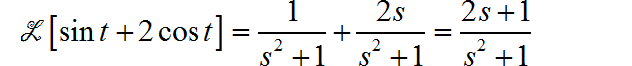
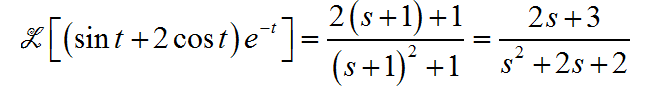
(3) 利用 Laplace的时移特性
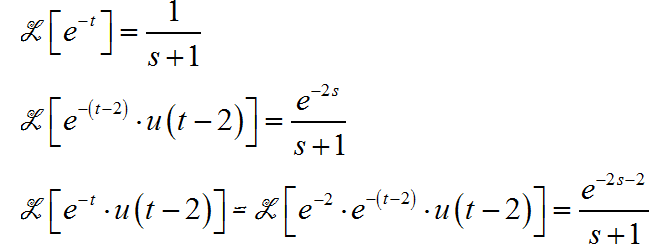
(4)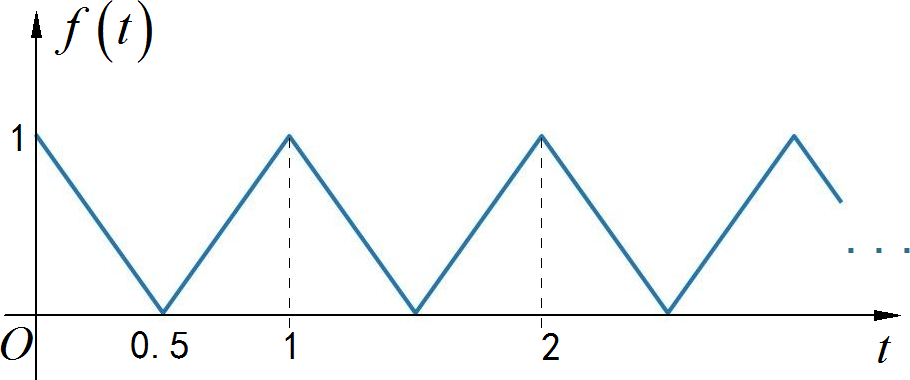
▲ 图1.3.1 右边周期信号对于信号单个周期内 信号求解它对应的 Laplace变换。对它求导,得到如下波形:

▲ 图1.3.2 信号单个周期导数信号根据 Laplace 变换时移特性,可以写出该信号对应的 Laplace 变换。
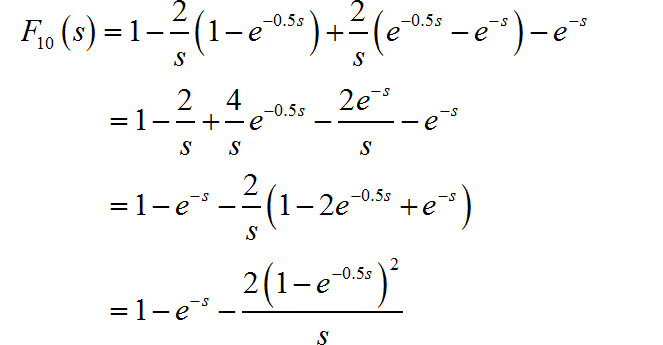
那么根据 Laplace 变换的微分、积分定理, 原信号单个周期信号的 Laplace 变换为:
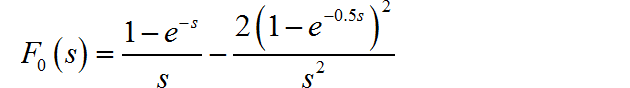
那么, 右边周期信号的 Laplace 变换为:
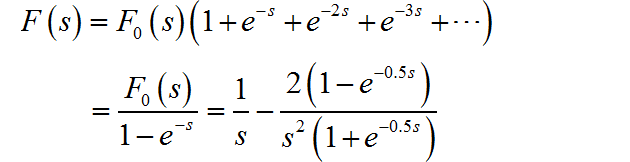
(5)
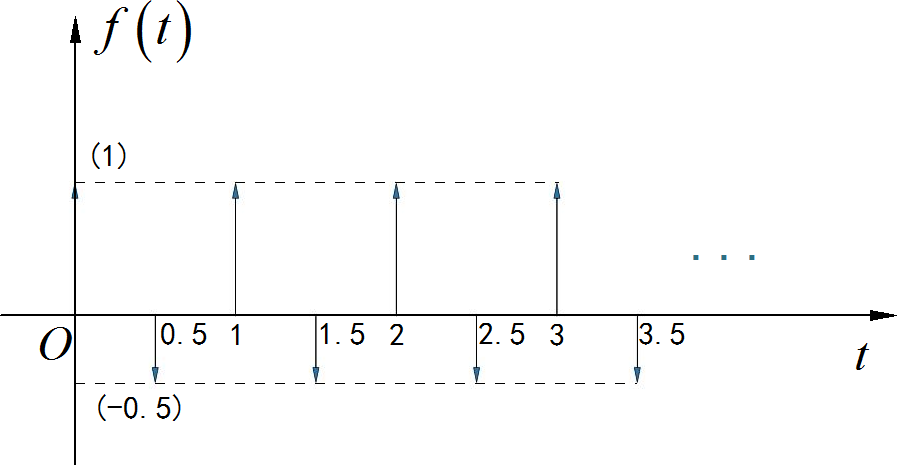
▲ 图1.3.3 右边周期脉冲信号单个周期信号的 Laplace 变换为:

那么,周期信号的 Laplace 变换为:
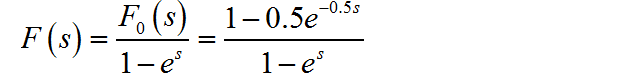
(1)
根据信号的表达式判断它满足终值存在条件, 根据 Laplace 初值和终值定理可得:

(2)
信号的初值为:
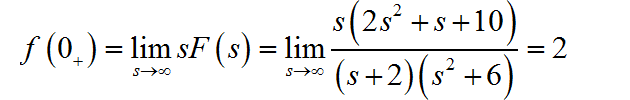
根据信号的表达式判断它不满足终值存在条件, 因为它具有两个位于虚轴上的共轭极点。所以信号终值不存在。
(3)
先 使用长除方法, 将原 Laplace 有理分式拆分成一个常量和一个真分式:
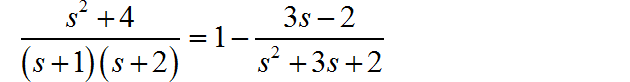
根据其中的真分式计算信号的初值与终值:
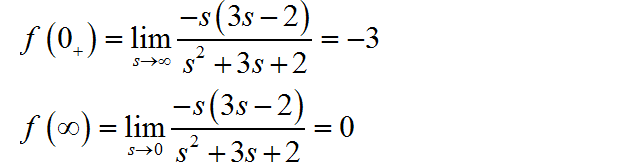
(4)
由于信号的 Laplace 变换中包括有 ,所以它可以看成 往右平移时间 1 所形成的信号。由此可以判断该信号的初值 。
由于该信号包括位于 s 复平面 虚轴右侧极点,以及位于原点的二阶极点, 所以该信号的终值不存在。
信号与系统 2023(春季) 作业要求 - 第10次作业: https://zhuoqing.blog.csdn.net/article/details/130410200
