麦克斯韦方程,是所有电磁理论的基础,其微分形式如下图所示。
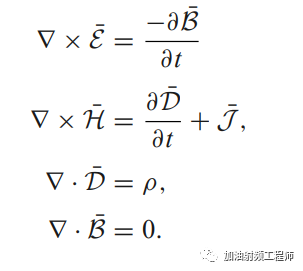
都说麦克斯韦方程是世界上最美的公式之一,可是这几个方程,到底能让我们了解些什么呢?
在说这个问题之前,先来说说相量的概念。
欧拉公式告诉我们:
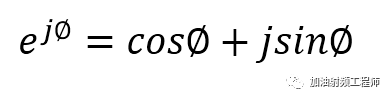
所以对于平面上的任一点Z,可以表示为:
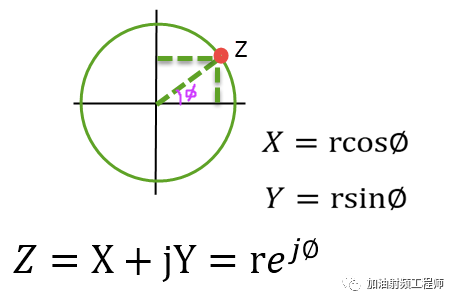
所以,对于一个实正弦信号,可以用下列形式表示:
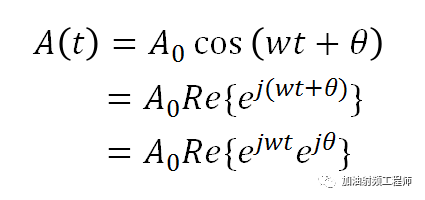
所谓使用相量表示,即:
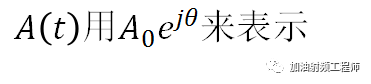
但是,也不是什么时候,都可以用相量进行表示。
从上面公式可知,A(t)的相量形式,省去了Re{}以及e(jwt)。
那什么时候,这两个可以省去呢?
一种情况是,大家都知道了,写与不写,大家都默认是有这两项的。
也就是说,使用相量形式的前提,是:
(1) 被表示的变量是一个实数,所以不需要将Re{}写出来
(2) 处理的系统是线性时不变系统,即变量的频率分量是不变的,因此,不需要把e(jwt)写出来。
所以,用相量来表示一个正弦信号时,只要写出其幅度和相位就可以了。
不过,虽然不用写出来,但是需要记住的是,其实这两项是存在的。如果对A(t)进行求导的话,不能忘记还有时间的存在,即:
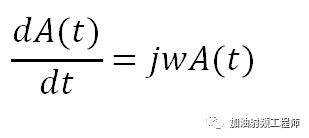
现在,用相量来对麦克斯韦方程中的第一个和第二个旋度方程进行处理。
为了简化分析,假设所分析区域中的电流和电荷都为0。
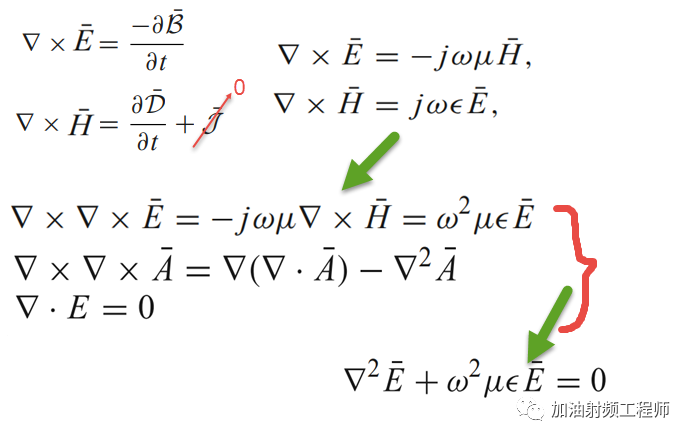
类似的推导,也可以得到:

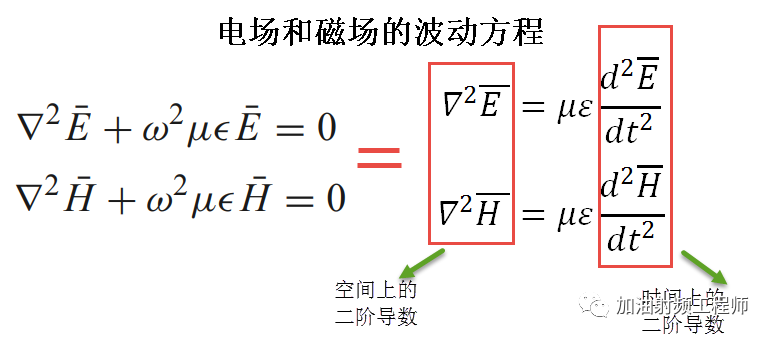
而这两个式子,就是电磁场的波动方程,或者说是波动方程的相量形式。
波动方程是一个微分方程,这个微分方程,可将变量在时间上的二阶导数与其在空间上的二阶导数联系起来。
定义波数:
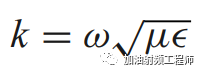
在无耗的媒介中,介电常数和磁导率都为实数,因此k也为实数。
假设电场只存在于x方向,且只随z的变化而变化。
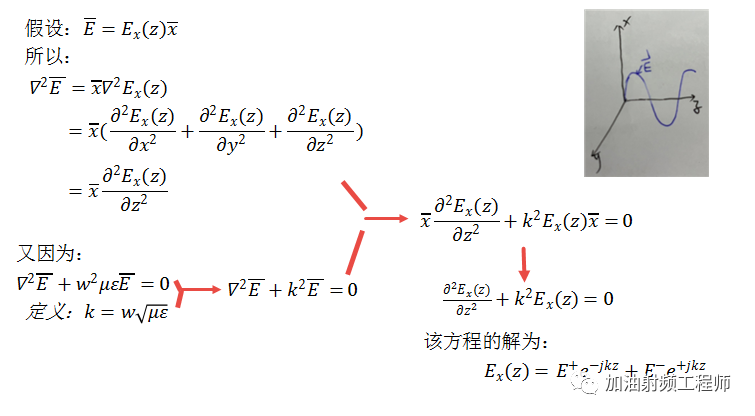
把上面的相量形式改成正常形式后,则:
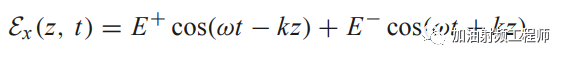
上面式子中的第一项,表示前向波,即随着时间的增加,波沿着+z轴传播;而第二项,表示后向波,即随着时间的增加,波沿着-z轴传播。
此时,相速,即波的相位在空间中传播的速度如下式所示:
而电磁波的波长,则定义为在固定的时间点,两个波峰或者波谷的距离。即:
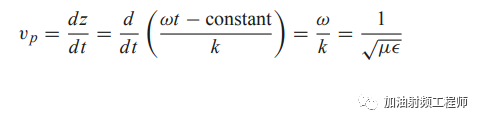
因此,由麦克斯韦方程,可以得到电磁场的波动方程,对波动方程进行求解,即可以得到电场和磁场在时间和空间上的传播形式。