
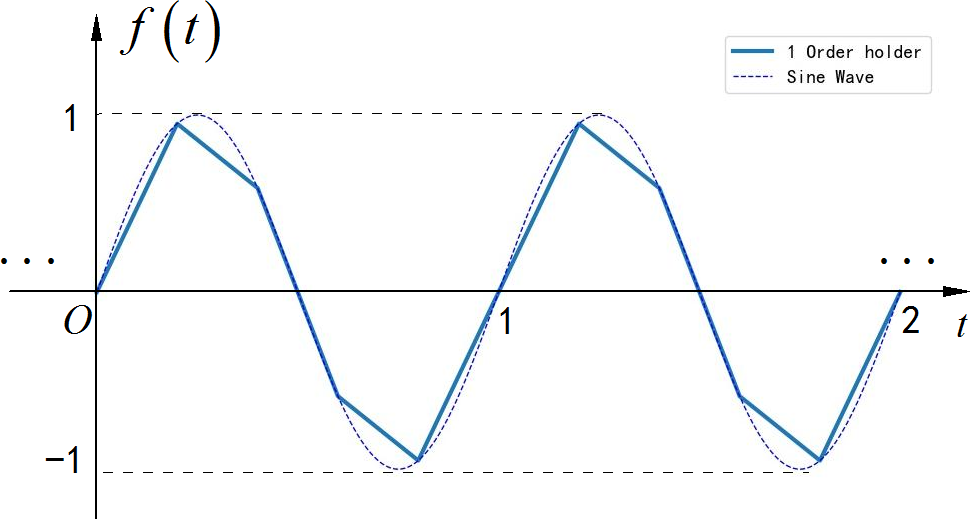
▲ 图1.1.1 一阶保持恢复的采样信号◎ 解答
(1) 对信号的一阶保持回复, 可以看成对采样的离散信号 使用 三角脉冲信号进行卷积。根据题目给定的信号采样参数, 对应的三角脉冲信号的宽度为 (对应 5MHz 的周期)。
对于频谱为 5MHz, 幅度为 1 的正弦波, 它的频谱为:
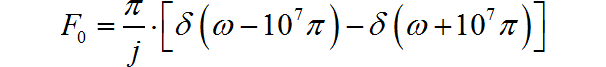
由于 是一个纯虚数, 所以下面绘制出 对应的波形:
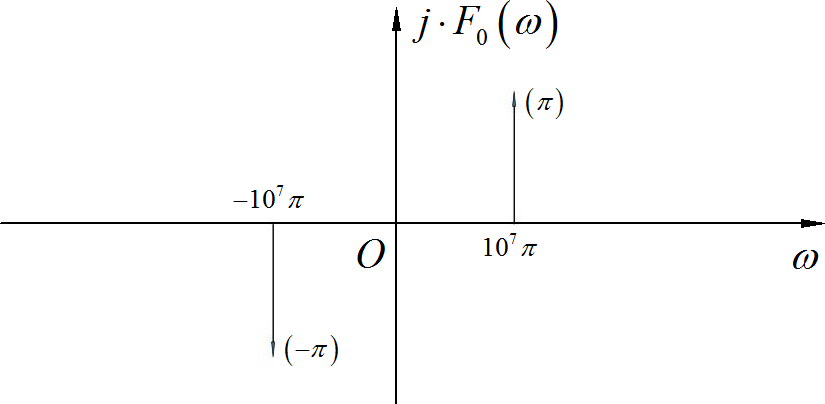
▲ 图1.1.2 正弦波的频谱对其进行 25MHz 的理想采样, 对应的频谱为:
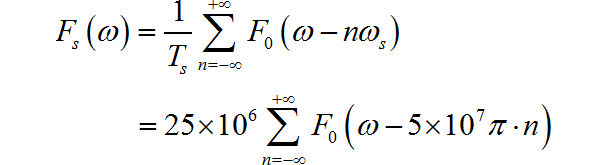
对应的频谱绘制如下, 为了显示出周期延拓,频率轴的尺度进行了压缩。
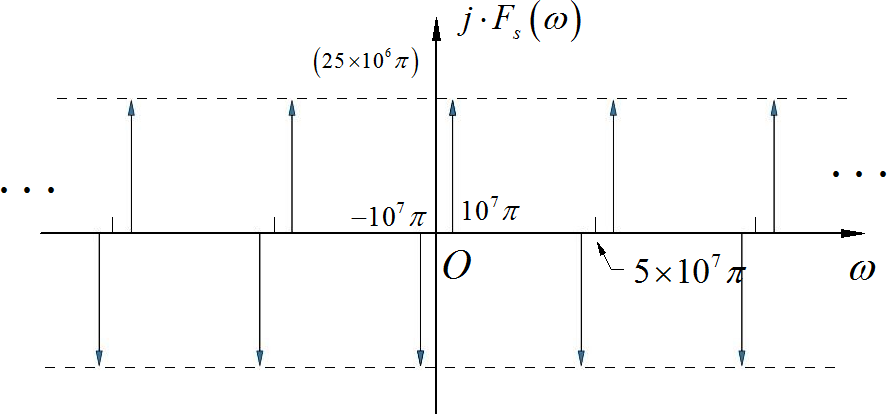
▲ 图1.1.3 理想采样信号频谱对采样信号进行一阶保持, 等效于和采样周期等宽的三角脉冲信号进行卷积。如下图所示:
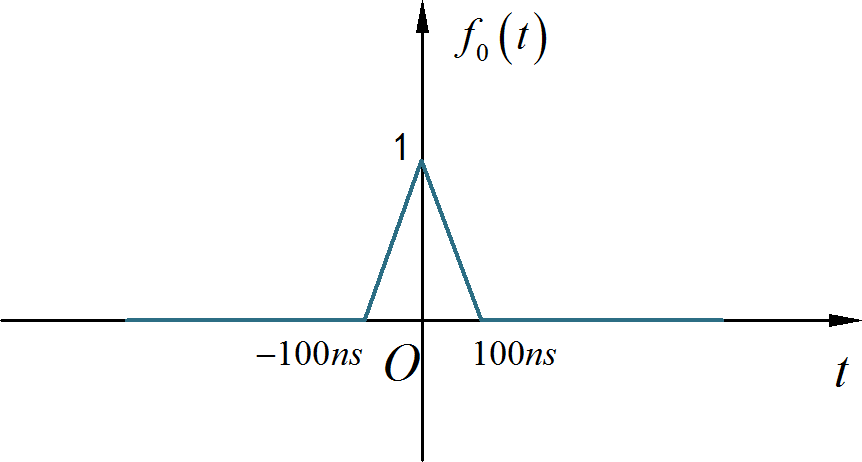
▲ 图1.1.4 一阶保持对应的插值三角脉冲信号该信号的频谱为:
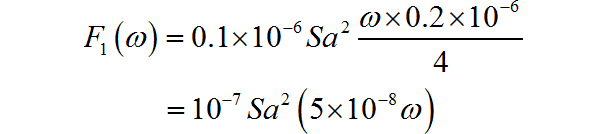
因此, 一阶保持信号的频谱为:
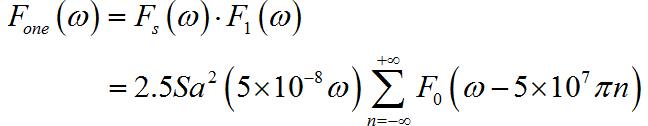
可以看出一阶保持信号的频谱是在原来周期冲击频谱的基础上, 前面乘以 加权系数,下面将该 sinc 函数与周期频谱绘制在一起, 也可以看到恢复信号的频谱主要包含有原信号 以及高次谐波, 但高次谐波分量被衰减较多(随着 分之一衰减)。所以绘制出来的信号频谱应该与原始 5MHz 正弦波频谱基本上一样, 高次谐波看不出来。
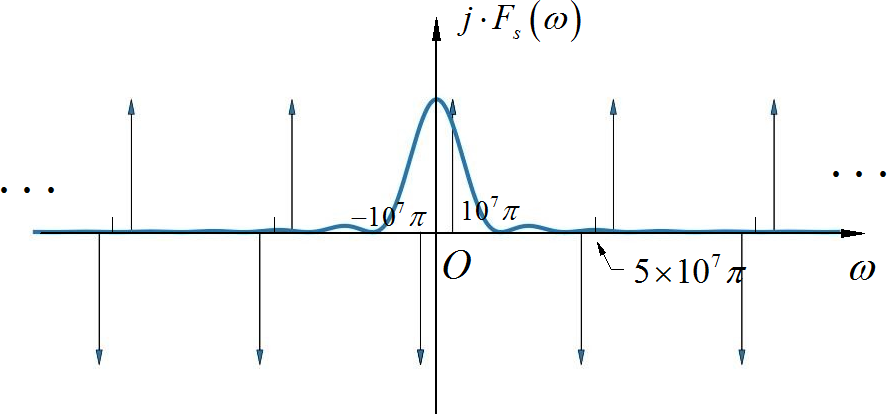
▲ 图1.1.5 将Sinc函数加权信号与理想采样对应的周期频谱绘制在一起下面是将一阶保持恢复信号的频谱绘制出来, 对应的高频谐波频谱省略了, 它们太小了。请注意, 基波冲激频谱的强度,由原来的 变成了 , 幅值有所衰减。
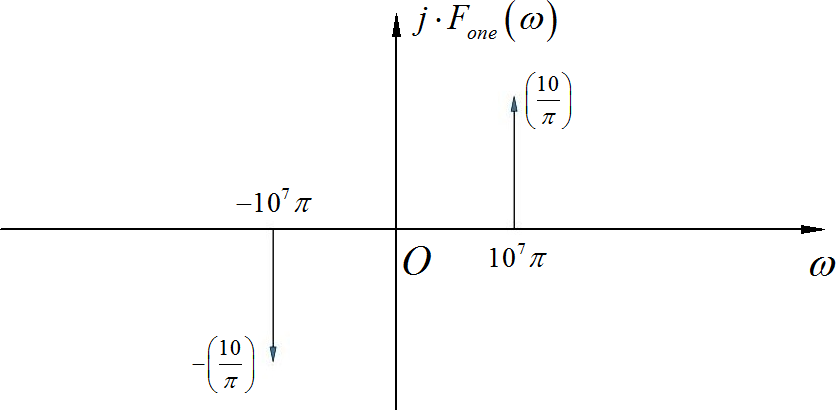
▲ 图1.1.6 一阶保持信号频谱(省略了高斯谐波)(2) 从一阶保持波形中,恢复原来的 5MHz 的正弦波,对应的补偿滤波器的频谱特性如下:
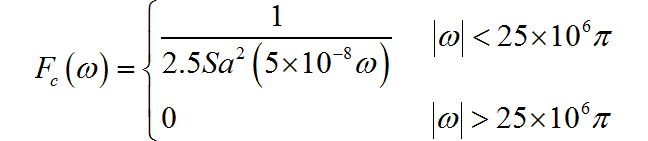
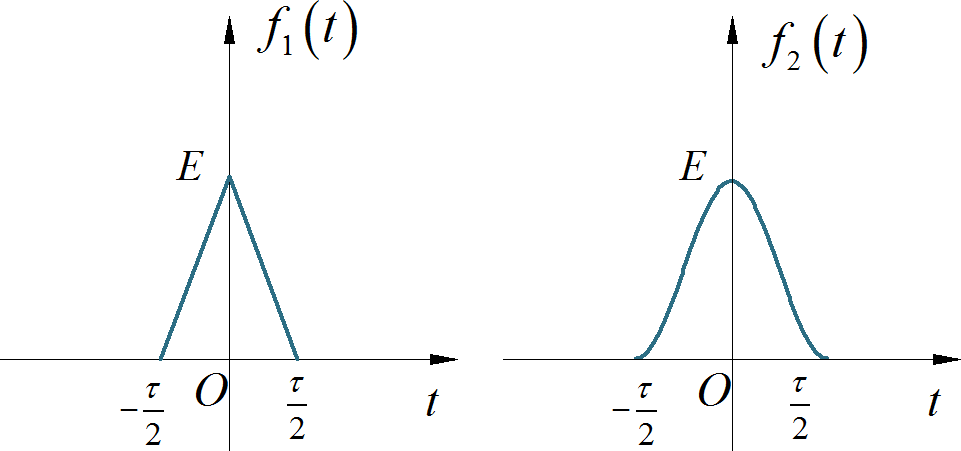
▲ 图1.1.7 三角形与升余弦脉冲信号◎ 解答:
查找典型信号频谱, 可以分别得到单个三角脉冲以及升余弦脉冲信号的频谱表达式。单个三角脉冲信号的频谱为:
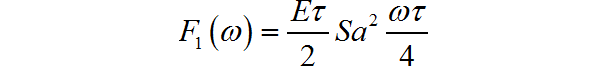
单个升余弦脉冲信号的频谱为:
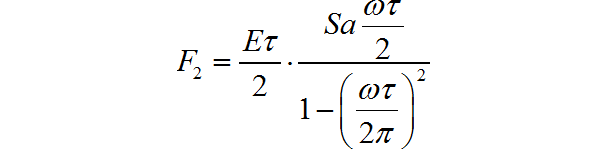
将它们使用 进行采样后,对应的频谱为:
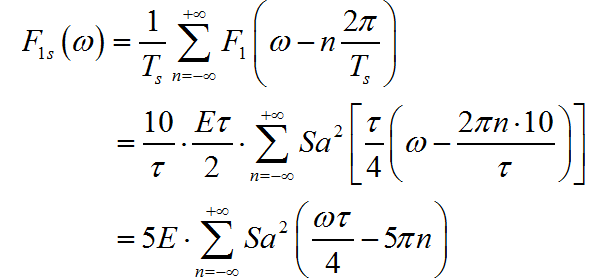
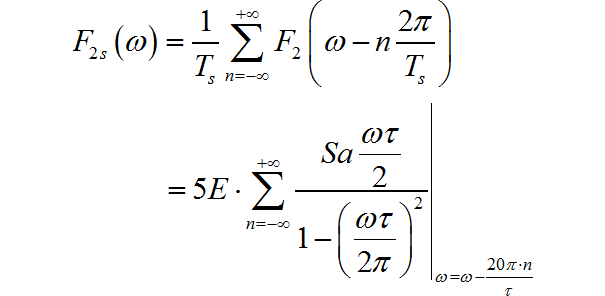
下面使用 Python 程序绘制上面频谱图。为了便于绘制, 设置频谱中的参数 。
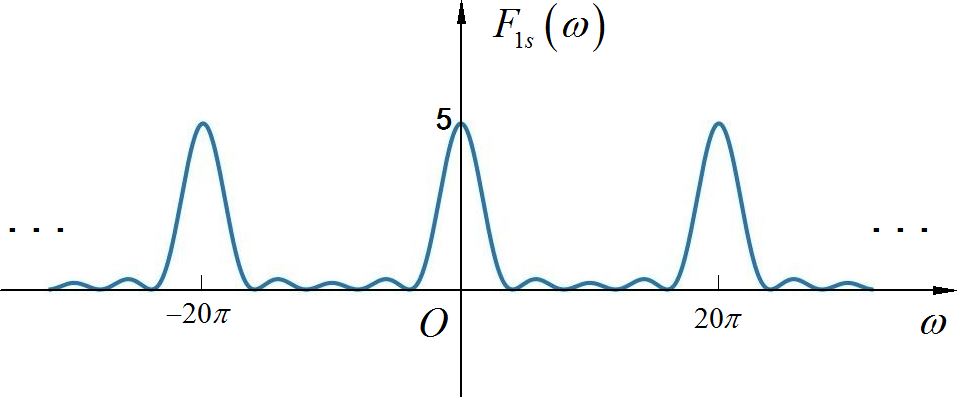
▲ 图1.1.7 三角脉冲信号采样信号频谱示意图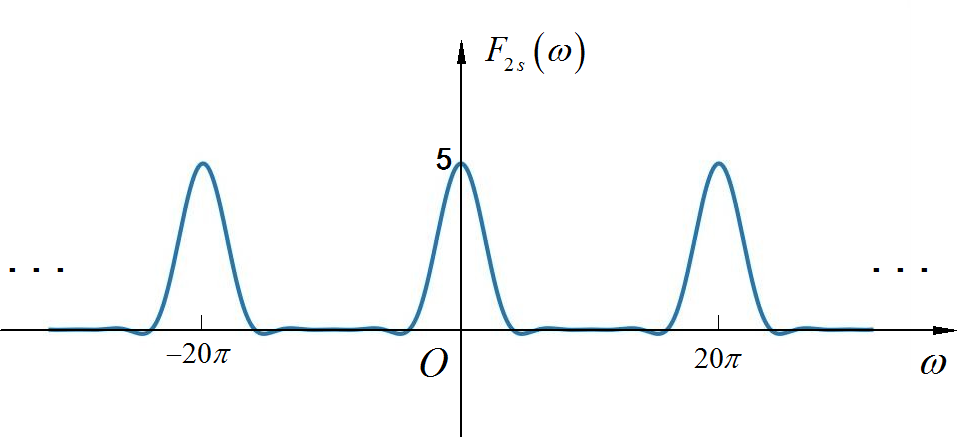
▲ 图1.1.8 升余弦脉冲信号采样信号频谱示意图◎ 求解:
(1)
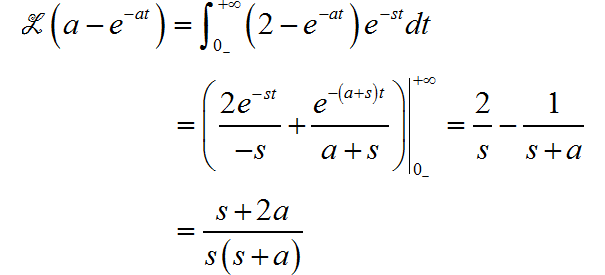
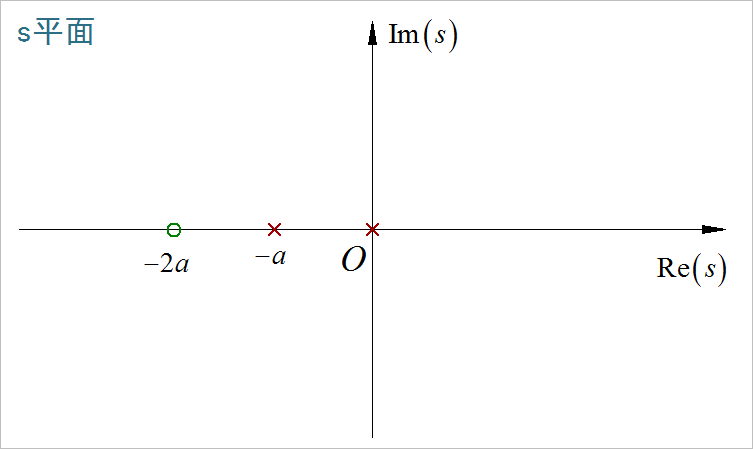
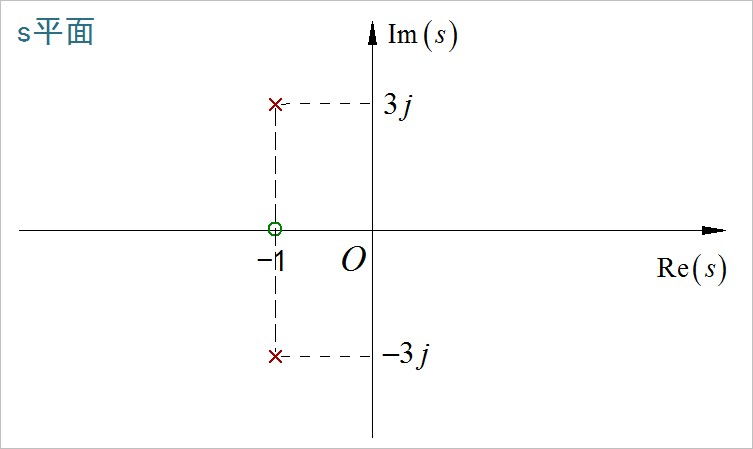
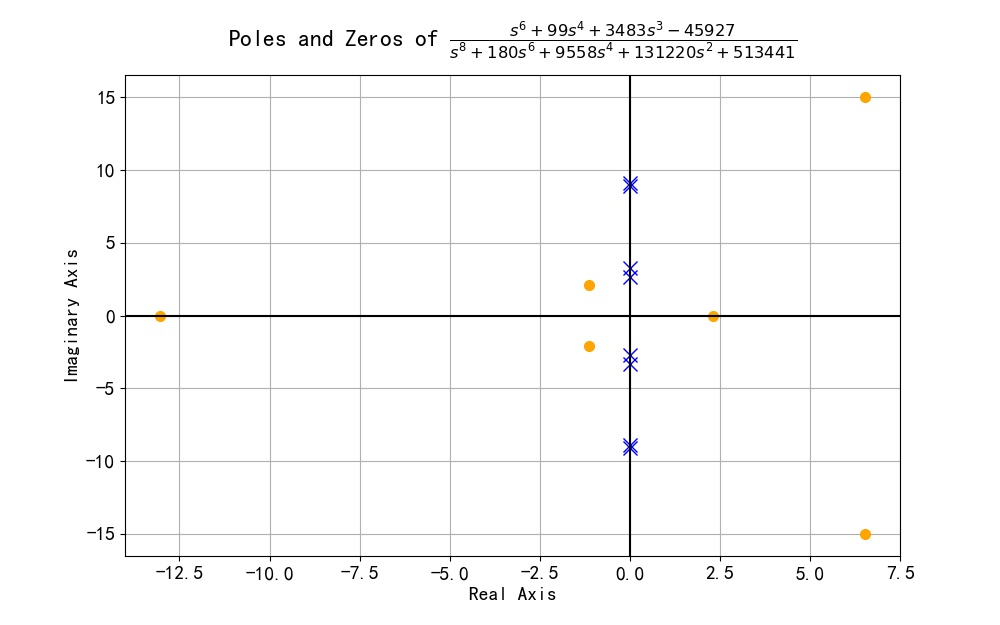
▲ 图1.2.1 Laplace变换结果中的零极点(2)
下面直接根据 sin(t), cos(t) 的Laplace的变换结果, 利用 Laplace 线性性, 可以得到:
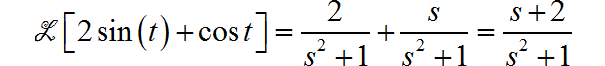
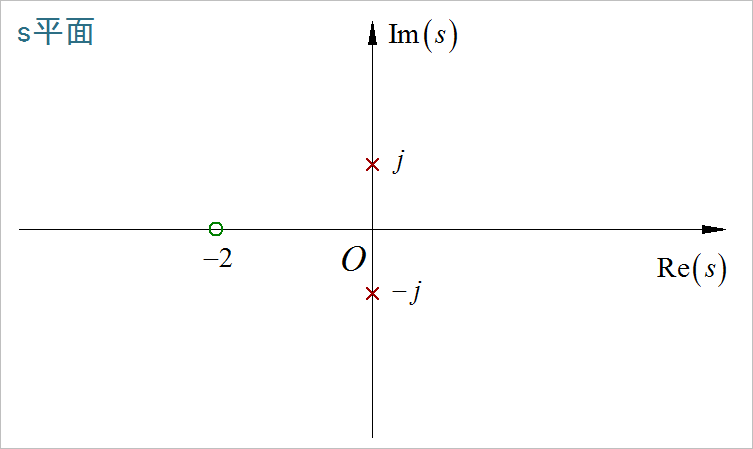
(3)
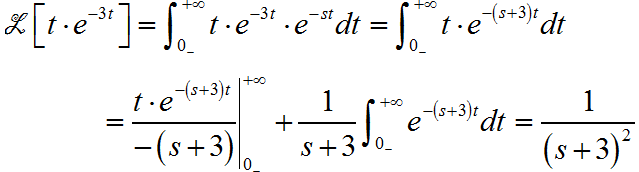
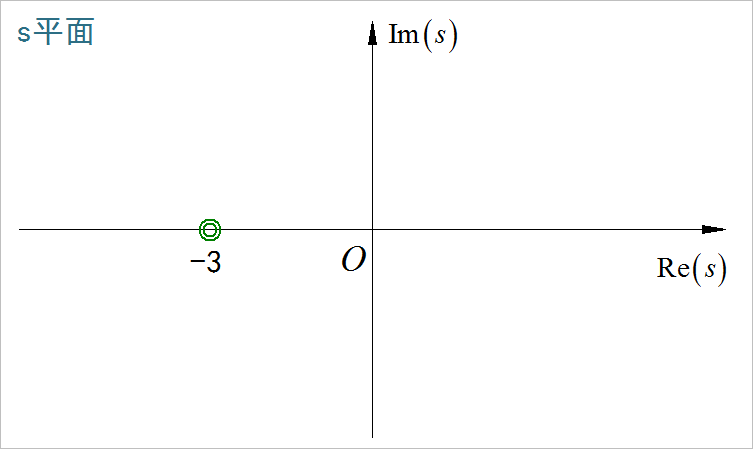
(4)
(5)
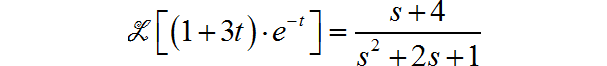
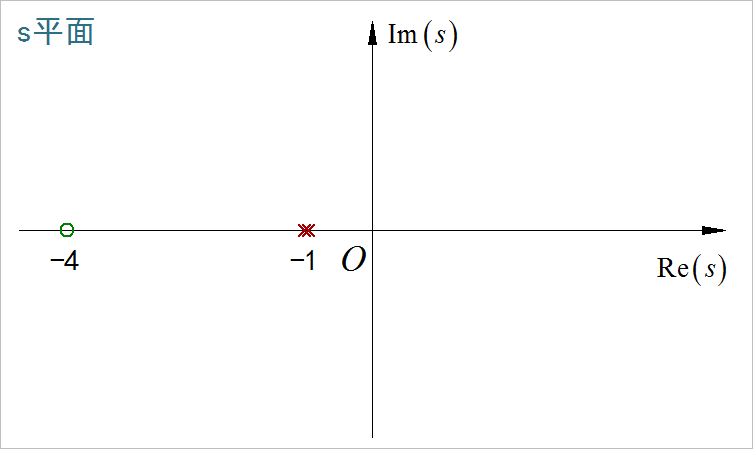
(6)
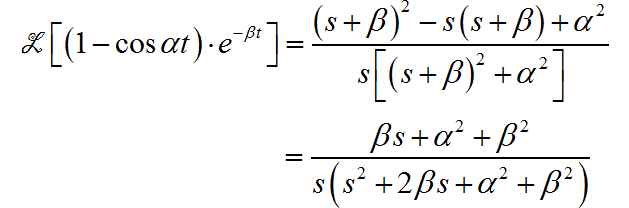
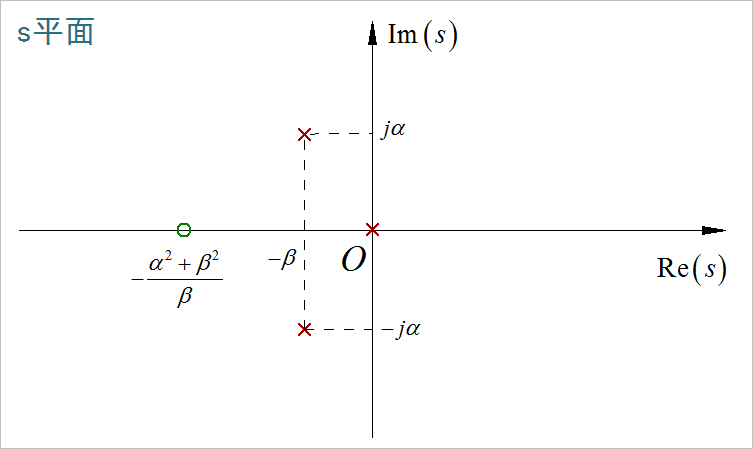
(7)
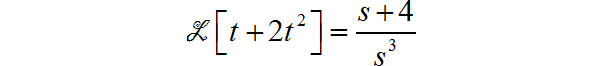
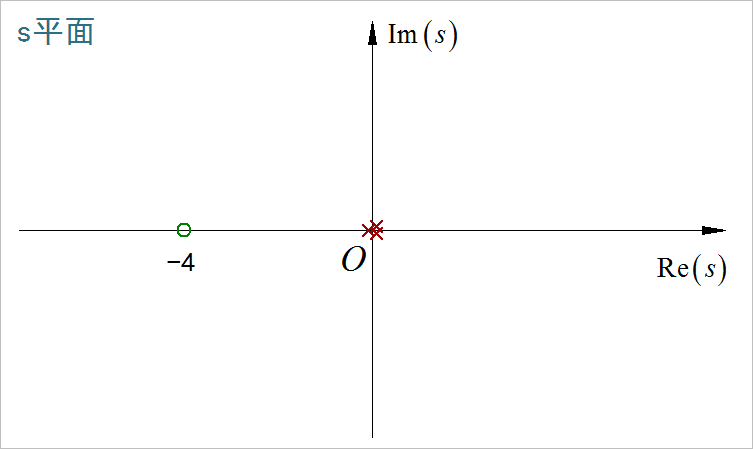
(8)
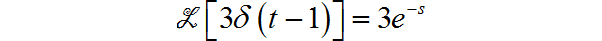
(9)
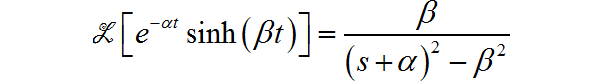
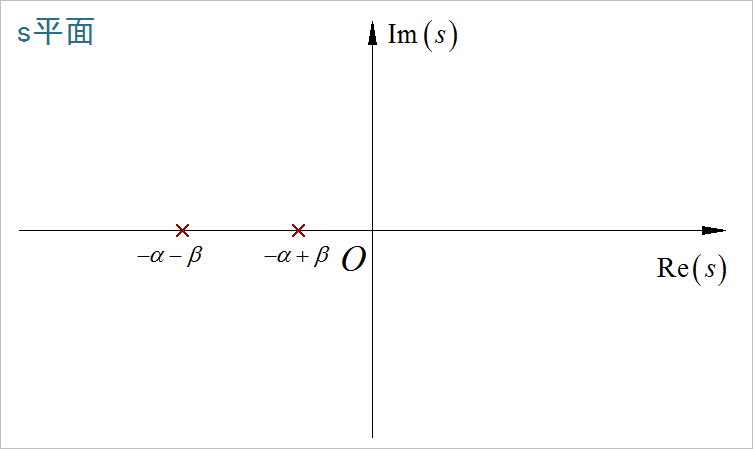
(10)
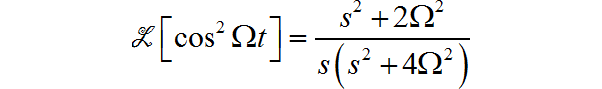
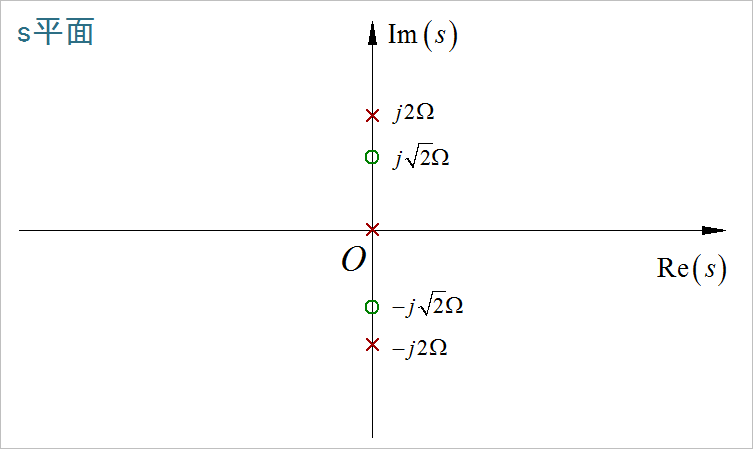
(11)
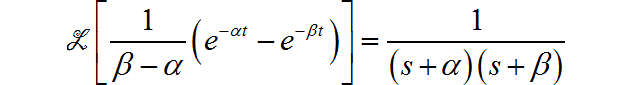
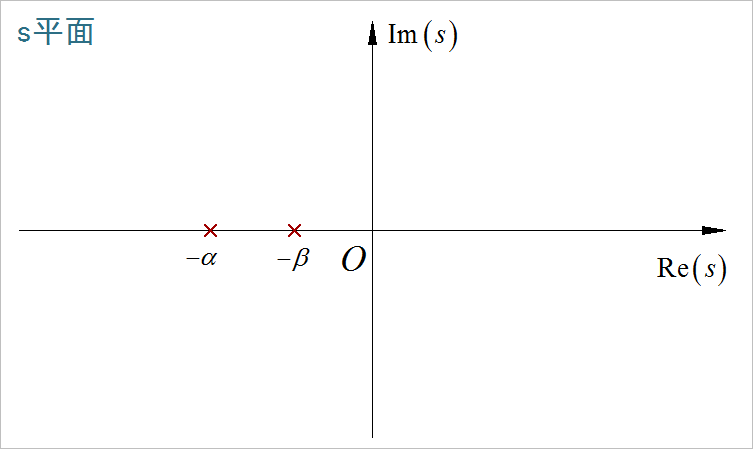
(12)
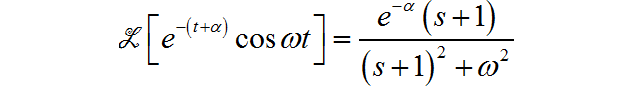
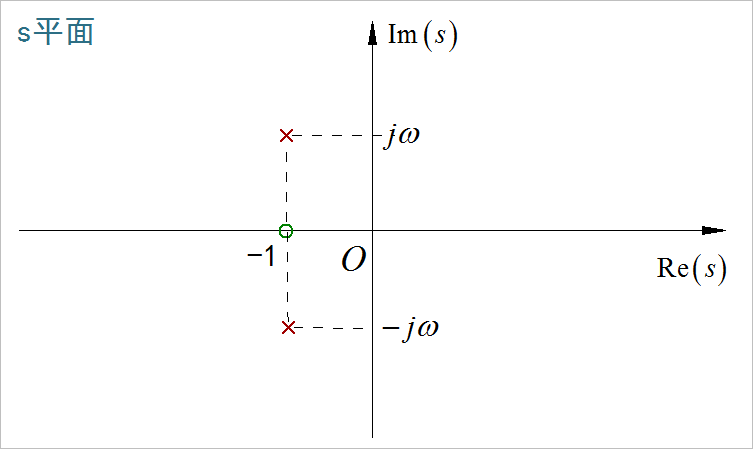
(13)
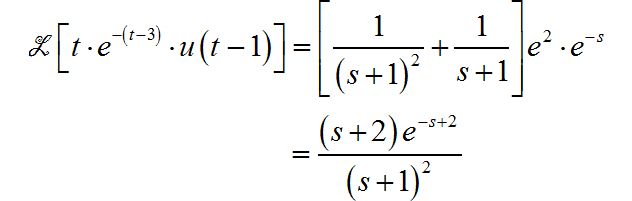
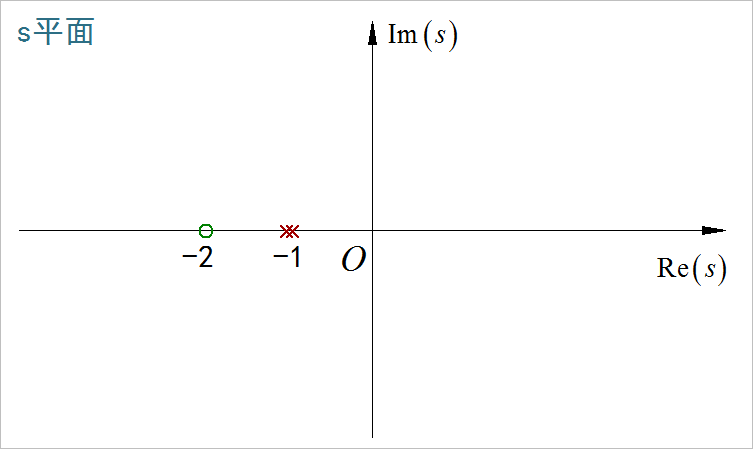
(14)
这个题目实际上对应的 Laplace 变换 s 域平移和尺度性质。
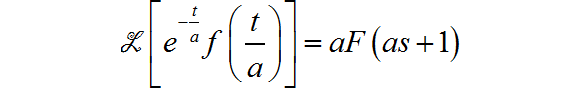
(15)
这个题目是通过 Python 中 的 laplace_transform 进行推导化简的, 手工推导实在太复杂了。(我没有敢尝试手工推导)
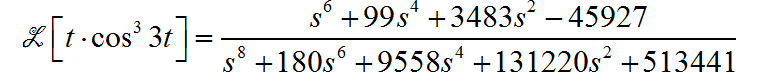
下面应用 Laplace 变换的性质帮助求解。先根据三角恒等式
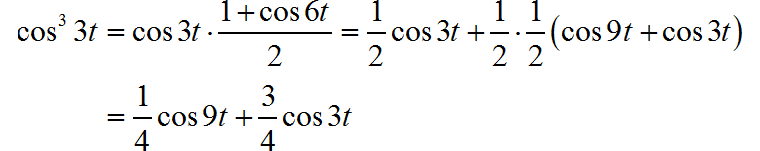
所以
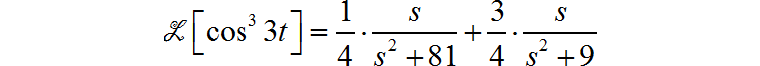
再由 s 域微分性质,可得:
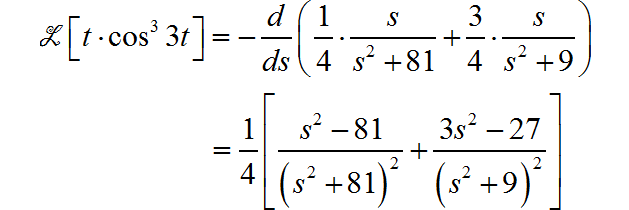
对上面的表达式进行化简, 可以得到前面相同的表达式。
下面利用数值求解,或者所有的零点和极点。
六个零点的数值结果:
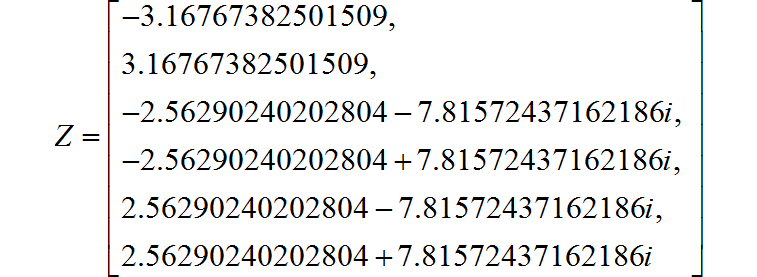
八个极点的数值结果:
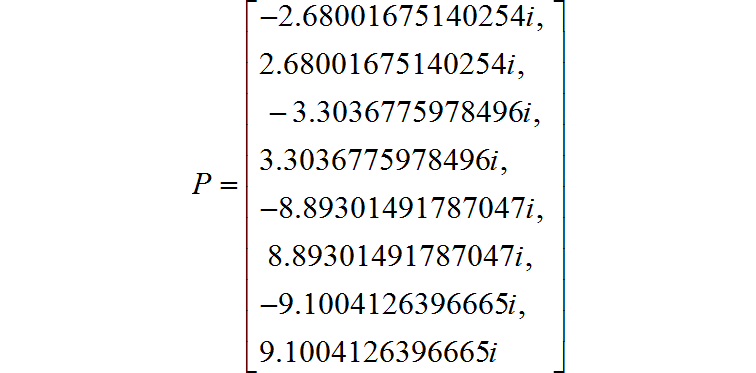
(16)
根据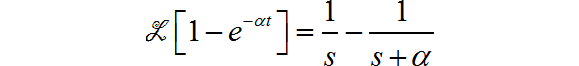
再根据 s 域的积分性质, 得:
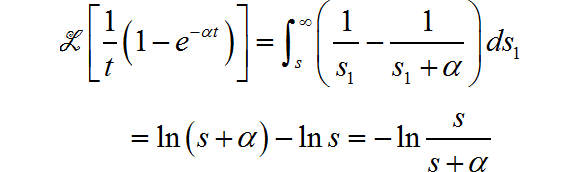
(17)
根据
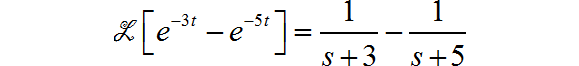
再根据 s 域的积分性质, 得:
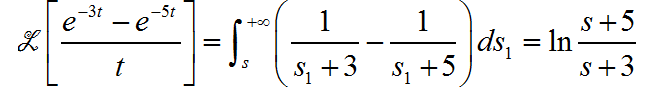
(18)
根据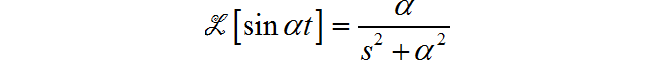
在根据 s 域内的积分性质,可得:
(19)
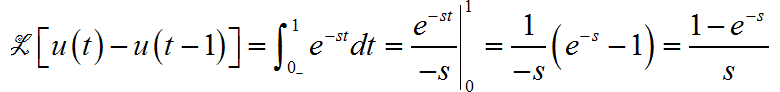
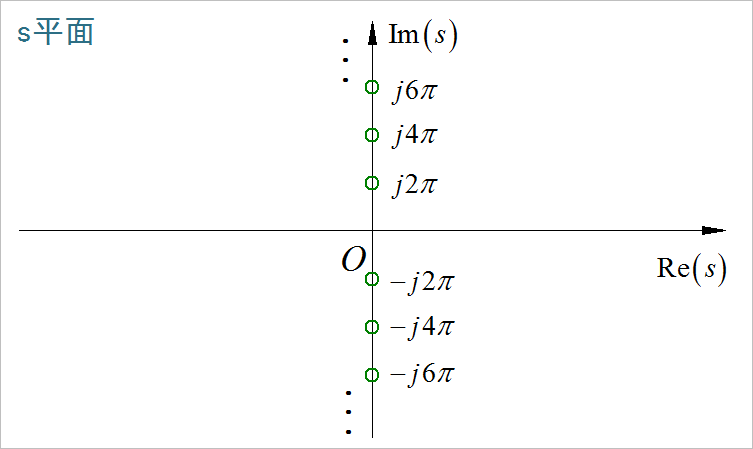
◎ 求解:
(1)
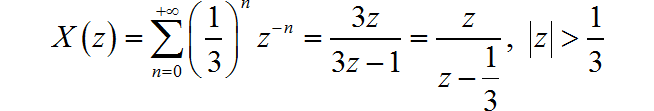
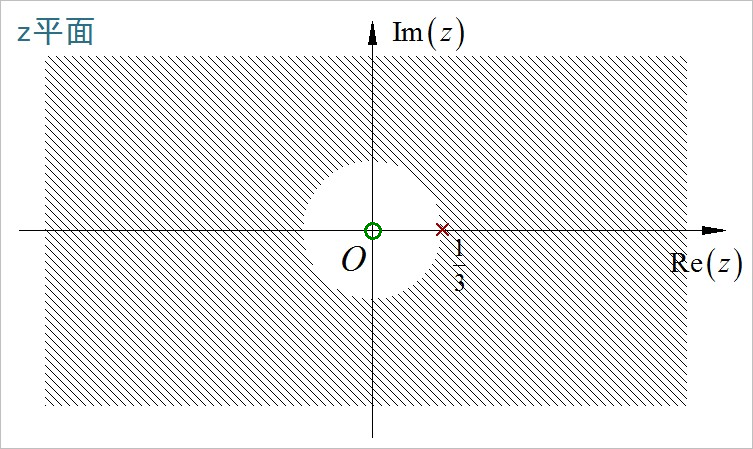
(2)
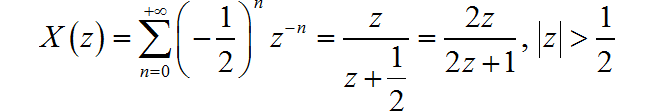
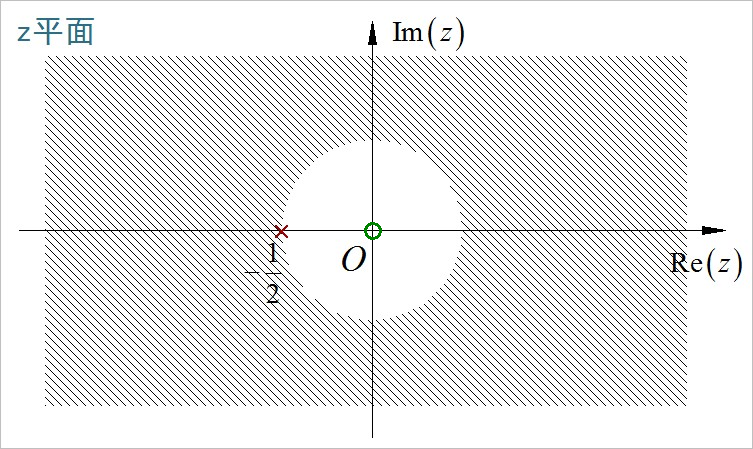
(3)
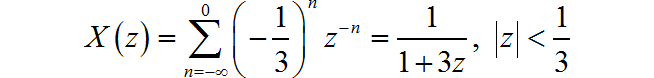
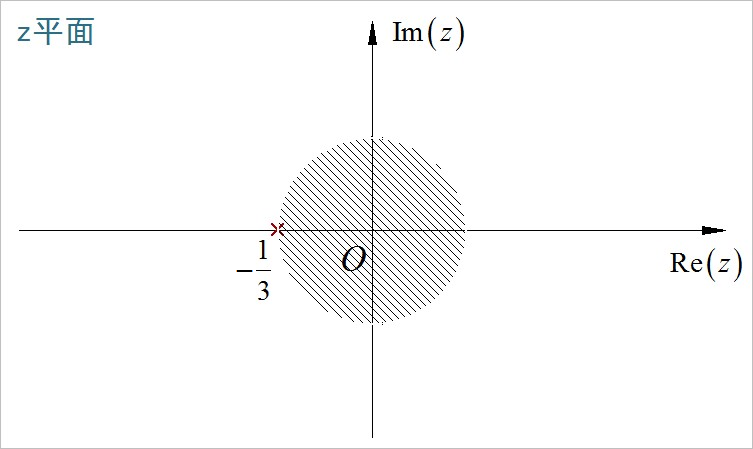
(4)
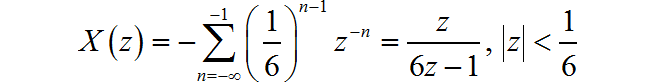
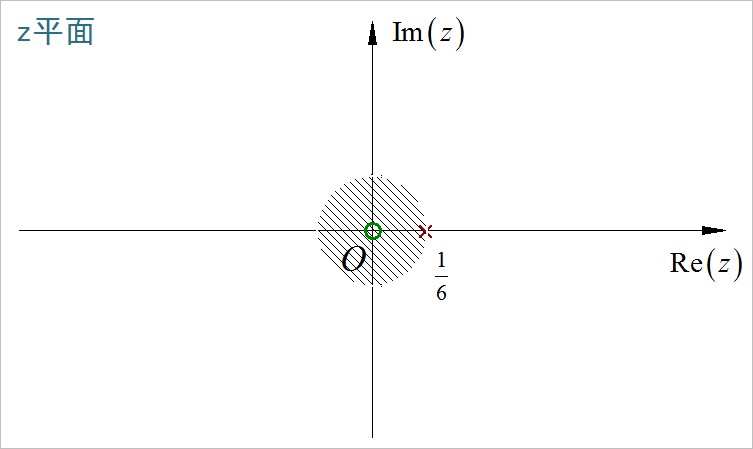
(5)
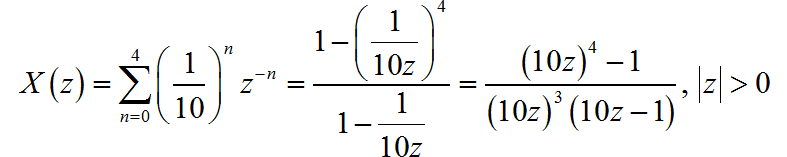
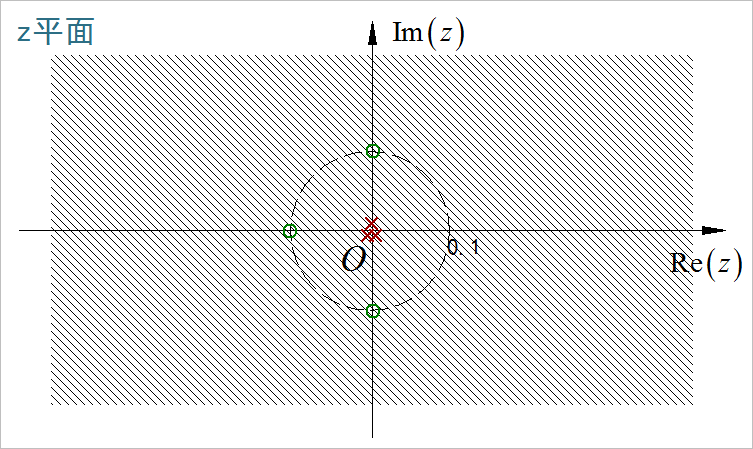
(6)
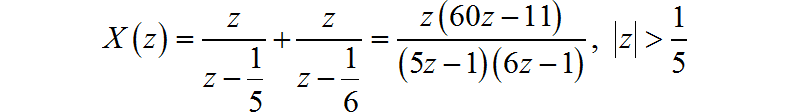
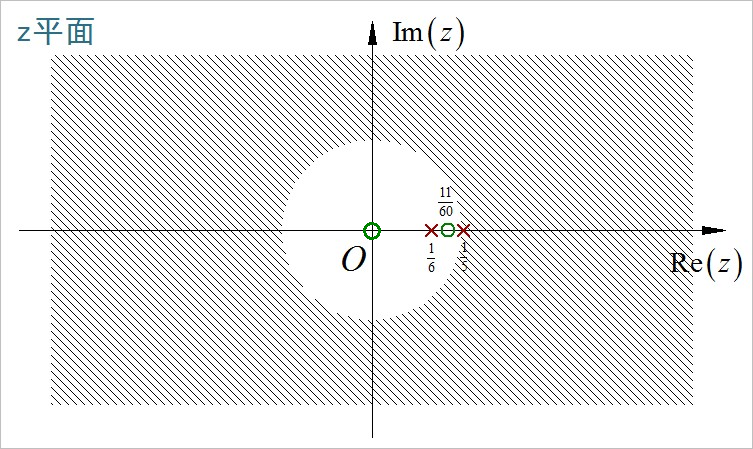
(7)
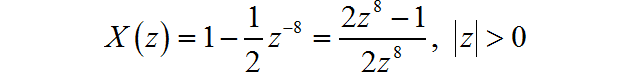
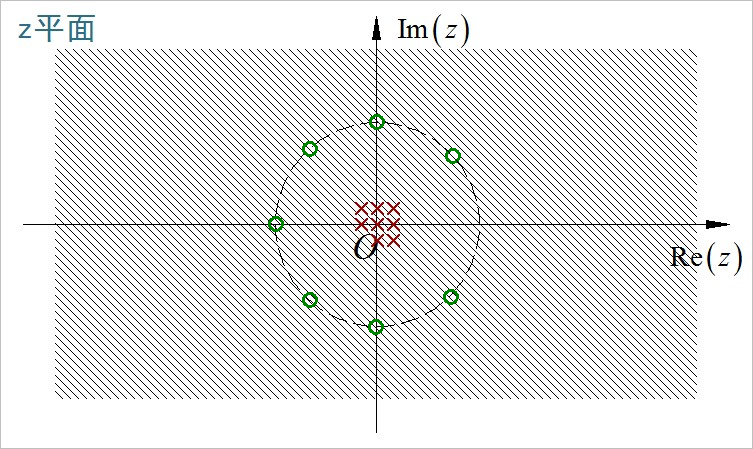
(8)
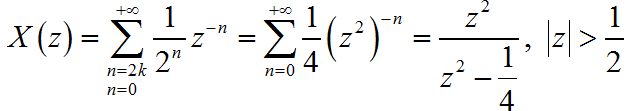
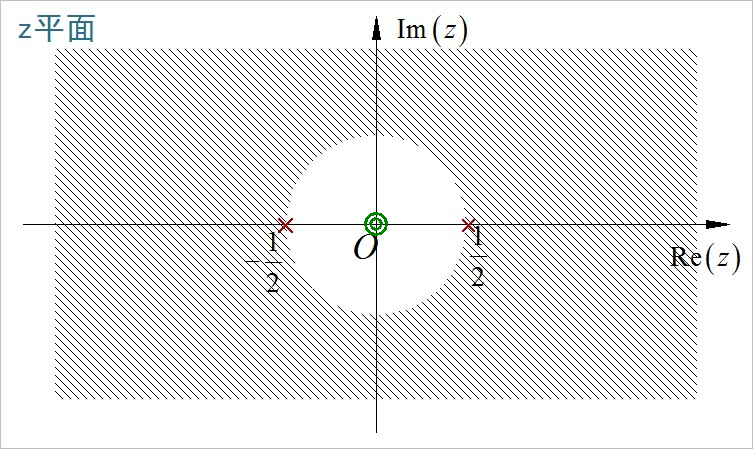
(9)
将双边序列分成左边序列和右边序列, 分别各自求出对应的 z 变换, 然后在相加在一起。
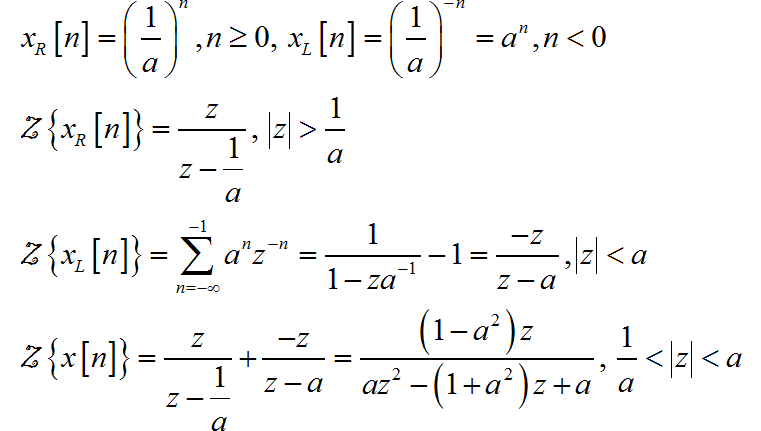
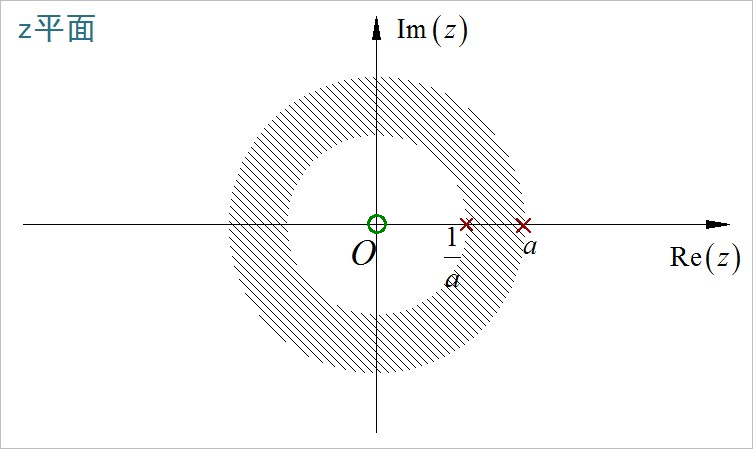
信号与系统 2023(春季) 作业要求 - 第九次作业: https://zhuoqing.blog.csdn.net/article/details/130270625
[2]信号与系统分析2022春季作业-参考答案:第九次作业: https://zhuoqing.blog.csdn.net/article/details/124284763