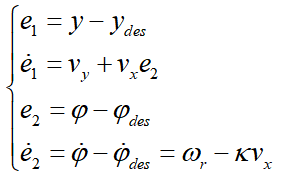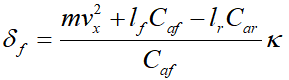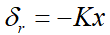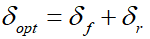--关注、星标、回复“40429”--
↓↓领取:《汽车驾驶自动化分级》(GB/T 40429-2021)↓↓
编辑语:后台回复“仿真”即可领取本文涉及仿真模型
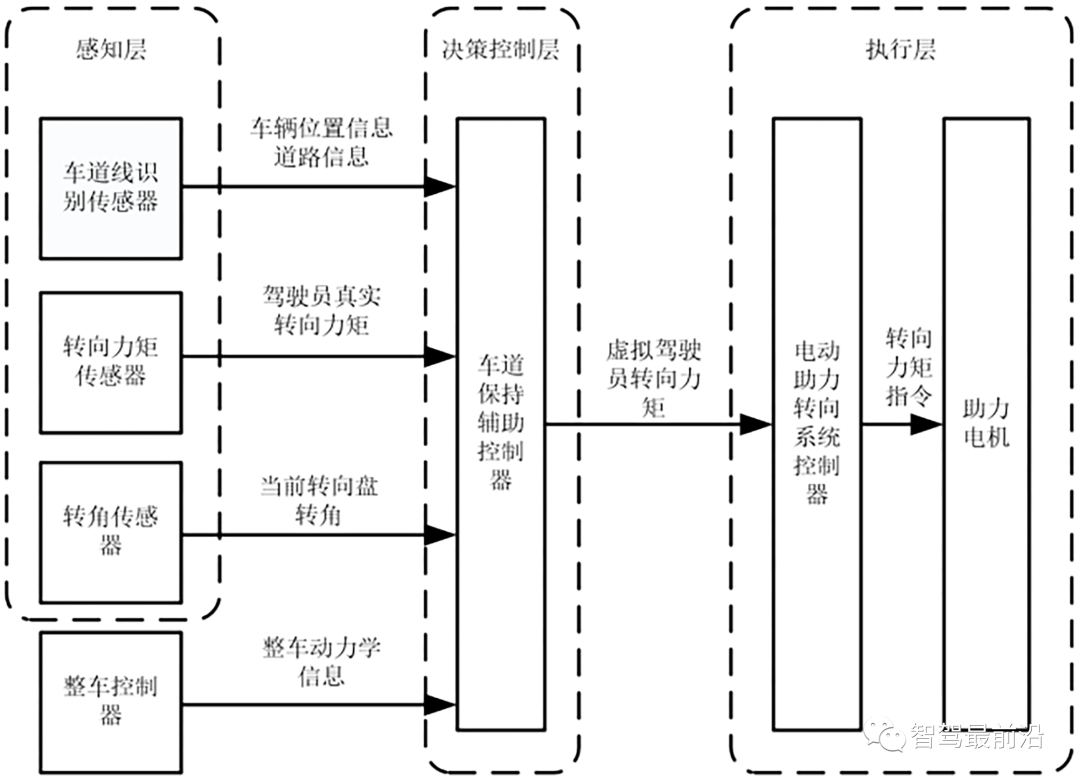
车道保持辅助(Lane keeping assistance,LKA)系统指的是通过摄像头检测本车相对期望的行车轨迹(如车道中心线)的横向运动状态,基于车辆横向动力学设计横向控制器,实时计算方向盘的期望转角大小和方向,实现LKA系统的闭环控制,使车辆保持在车道内行驶。LKA在一定程度上缓解了驾驶强度,辅助驾驶员实现车道的跟踪,并适时提供车道偏离预警,保证车辆能够在当前车道内稳定行驶,从而提升驾乘的安全性和舒适性。LKA是自动驾驶车辆运动控制的一个必不可少的组成部分,其主要目标是保证自动驾驶车辆在道路上行驶时不发生过大的横向位置误差与横摆角误差,将车辆实际行驶轨迹与道路轨迹进行对比分析,计算出车辆行驶过程中的横向位置误差与横摆角误差,通过LKA控制算法,计算出最理想的前轮转角,并通过线控转向系统控制车辆不断地调整车辆的转向角达到期望值,以减小车辆在行驶过程中产生的横向位置误差与横摆角误差,在道路曲率发生变化时,保障自动驾驶车辆的方向与位置始终跟随道路曲率变化处于理想状态。因此,采用如图 1所示的控制框图,可将LKA系统分为感知层、决策控制层与执行层。感知层采集车道线信息、转向系统状态和车辆运动状态;决策控制层对采集的信息进行处理,计算所需的辅助转向力矩或转向角;执行层控制线控转向系统实现车辆转向控制,使车辆稳定地行驶在正常轨道内。通过本实训项目,了解LKA系统的工作原理,能够建立车辆的二自由度模型和预瞄驾驶员模型,并利用预瞄的曲率、横向偏差和车道中心线与车辆之间的相对偏航角,设计前馈与反馈相结合的控制策略,最终实现LKA系统的闭环仿真。
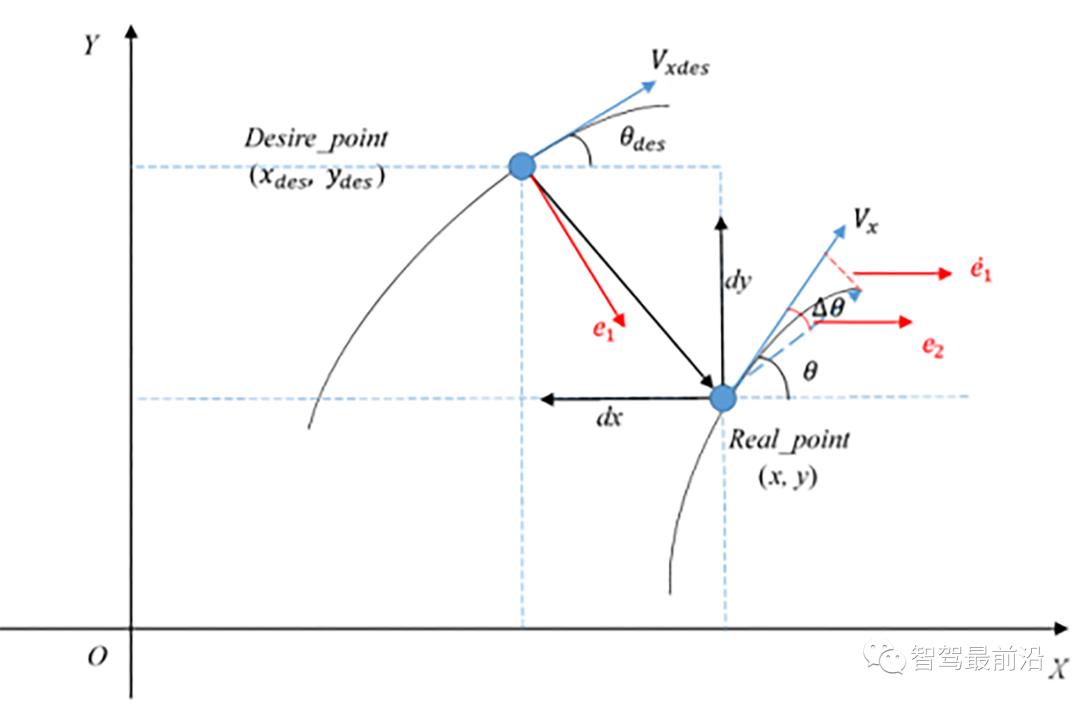
车道保持是一种路径跟踪任务,可以使用车辆横向动力学控制来完成。因此在搭建车辆动力学模型时,可以以相对于道路的方向和距离误差为状态变量建立动力学模型。假设横向控制误差即车辆距车道中心线的横向距离为e1,e2为航向误差,车道中心线的曲率为κ,车辆的横向控制误差示意图如下图所示,则航向误差为其中,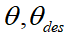 分别为实际的航向角与期望的航向角。横向误差变化率为定义系统状态为
分别为实际的航向角与期望的航向角。横向误差变化率为定义系统状态为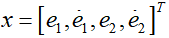 ,则车辆横向动力学模型写成状态空间形式为:基于动力学模型(6)即可设计LKA状态反馈控制器。
,则车辆横向动力学模型写成状态空间形式为:基于动力学模型(6)即可设计LKA状态反馈控制器。
假设道路曲率κ和系统状态x都是可测的,根据动力学模型(6)可见,由于系统矩阵B1和B2的特点以及环境的外界干扰输入,决定了无法通过前馈控制得到恒定的零稳态偏差。假设采用前馈与反馈相结合的方式实现LKA:可假设前馈控制器能让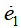 的前馈偏差为0,可得由此可见,在引入前馈控制(11)后,改变了系统的干扰增益矩阵,因此,针对系统(12)设计反馈控制可有效改善其抗干扰性能,与原始系统(6)相比,在系统(12)的基础上所设计的反馈控制系统性能将更优。将曲率当成环境干扰处理,接下来设计LQR反馈控制器。一般来说,状态反馈控制的效果比输出反馈控制的效果要好并且设计过程也较简单,而状态反馈控制的设计方法较多,可参考相关教材或书籍,本节中主要简单介绍LQR这种主流的控制方法。
的前馈偏差为0,可得由此可见,在引入前馈控制(11)后,改变了系统的干扰增益矩阵,因此,针对系统(12)设计反馈控制可有效改善其抗干扰性能,与原始系统(6)相比,在系统(12)的基础上所设计的反馈控制系统性能将更优。将曲率当成环境干扰处理,接下来设计LQR反馈控制器。一般来说,状态反馈控制的效果比输出反馈控制的效果要好并且设计过程也较简单,而状态反馈控制的设计方法较多,可参考相关教材或书籍,本节中主要简单介绍LQR这种主流的控制方法。3.2 LQR反馈控制
已知LKA系统的二自由度模型的状态方程为:
在LKA系统中,最优控制的目标是希望系统既能快速达到稳定状态,又希望控制量较小,所以选择如下的二次型代价函数:为了使性能指标最小化的最优控制器具有线性状态反馈形式,即控制输入为,将其代入到代价函数中,得到:当忽略环境中的曲率干扰项κ时,即假设车辆在直道上行驶,此时,根据(13)可得系统的闭环状态方程为令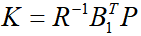 ,代入并整理可得黎卡提方程式中系统矩阵A、B1和权重矩阵Q、R都是已知量,由此便可以计算出正定矩阵P,进而得到LQR控制增益矩阵
,代入并整理可得黎卡提方程式中系统矩阵A、B1和权重矩阵Q、R都是已知量,由此便可以计算出正定矩阵P,进而得到LQR控制增益矩阵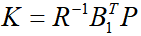 ,即得最优控制输入为u=-Kx。考虑到视觉传感器只可以检测状态e1和e2,即测量方程为因此,LKA系统存在状态不可测问题,可利用KF算法估计曲率以及系统状态,算法的具体实施过程可参考本书相关章节,在此不再赘述。则最终的基于观测器的状态反馈控制器为其中,
,即得最优控制输入为u=-Kx。考虑到视觉传感器只可以检测状态e1和e2,即测量方程为因此,LKA系统存在状态不可测问题,可利用KF算法估计曲率以及系统状态,算法的具体实施过程可参考本书相关章节,在此不再赘述。则最终的基于观测器的状态反馈控制器为其中,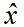 为系统状态x的估计值。
为系统状态x的估计值。
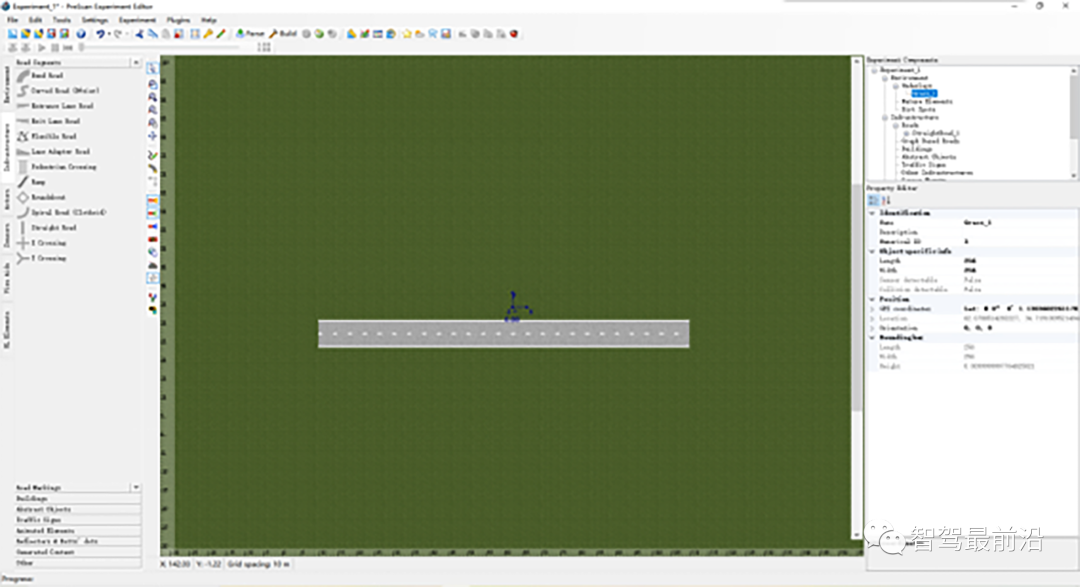
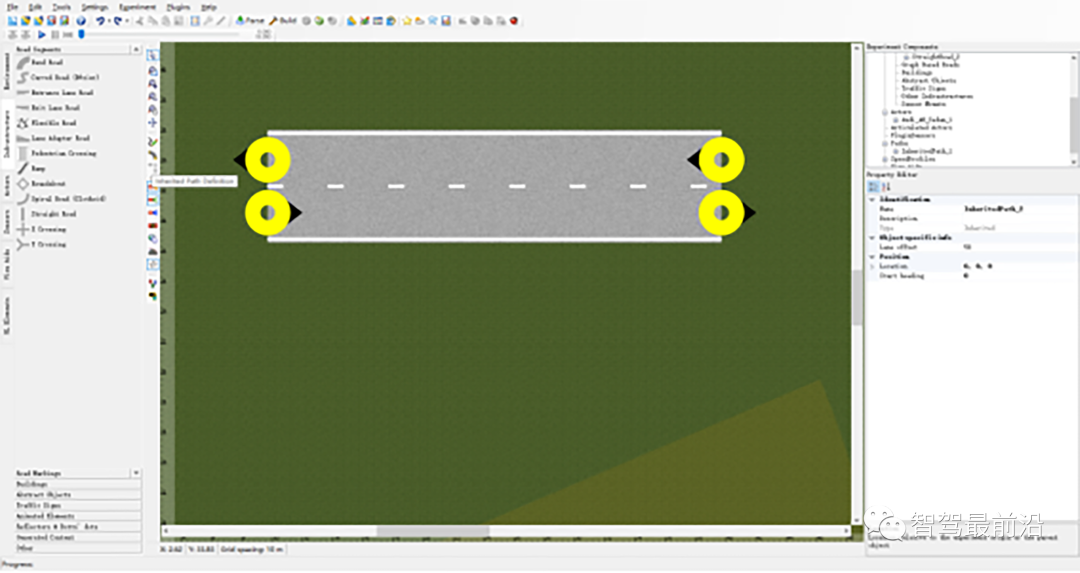
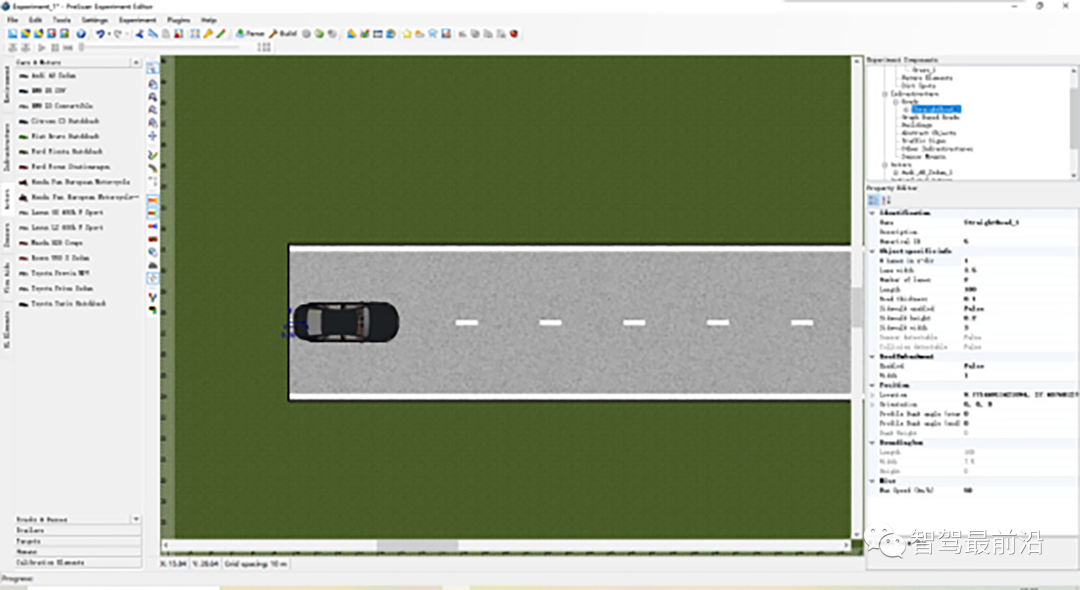
Prescan平台仿真主要步骤包括:创建仿真场景、建立传感器模型、运行仿真、增加控制系统等,下面介绍详细的Prescan仿真步骤(Step1~Step12)。Step1:打开Prescan程序,准备在Prescan软件中建立测试场景的仿真模型。首先双击Prescan GUI快捷方式,然后点击已打开的Prescan图标,在打开的GUI窗口中启动Prescan和MATLAB程序。Step2:通过拖拽放置的方式创建路网。为了简化测试场景,使用一条直线道路,对于弯道场地的建模原理也是一样,但需要设置道路曲率。建立行驶道路后,点击道路,在窗口的右侧可以设置道路的参数,包括道路长度、道路宽度、车道数量等。Step3:通过单击多个黄色圆圈来创建连续的汽车行驶轨迹,并通过“ESC”按键完成路径的创建过程。Step4:从车辆模型库中选择车辆模型,并放置到所创建的连续轨迹上,实现车辆与轨迹的关联,然后,对车辆模型参数、驾驶员模型参数、期望车速等进行设置。Step5:添加其他车辆和装饰元素完成整个仿真试验,通过控制动画演示进度控制条进行试验动画演示。同时,为了更好的观看车道保持的控制效果,对车辆添加跟踪视角。Step6:添加ALMS传感器,并设置传感器参数,以测量车道线信息。Step7:在prescan中执行仿真试验。先单击工具栏“Parse”按钮进行场景解析,通过后再单击“Build”按钮创建试验,一旦创建完成,即可通过simulink对该场景进行仿真、动画演示等。Step8:通过prescan GUI打开MATLAB/simulink,然后修改工作目录,再打开simulink仿真模型,如果MATLAB命令窗口显示“Compilation Sheet Generation Complete”则表示编译表已成功生成,进而可以完成在simulink环境下的仿真试验。如若修改场景后,每次都需要通过Regenerate工具更新模型。Step9:确定系统的状态变量。选择车辆相对道路的方向和距离误差为二自由度模型的状态变量,车辆距离车道中心线的横向距离和车辆的航向角偏差分别为e1和e2,状态变量可以表示为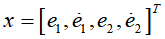 ,即:利用预瞄驾驶员模型和ALMS传感器可以检测状态横向距离偏差e1和航向角度偏差e2。Step10:在对车道保持进行控制时,为了更好地减小稳态误差,利用了前馈+反馈的控制方法。对于前馈控制可采用前文中已经详细描述的自适应前馈,其前馈输入的表达式为:Step11:对于反馈控制,利用LQR算法进行控制,接下来利用MATLAB函数lqr进行LQR控制器的求解,求解代码如下:
,即:利用预瞄驾驶员模型和ALMS传感器可以检测状态横向距离偏差e1和航向角度偏差e2。Step10:在对车道保持进行控制时,为了更好地减小稳态误差,利用了前馈+反馈的控制方法。对于前馈控制可采用前文中已经详细描述的自适应前馈,其前馈输入的表达式为:Step11:对于反馈控制,利用LQR算法进行控制,接下来利用MATLAB函数lqr进行LQR控制器的求解,求解代码如下:%% 车辆参数设置 %%M=1820; %%整车质量,kga=1.17; %%质心到前轴的距离,mb=1.77; %%质心到后轴的距离,mCf=52151; %%前轮胎侧偏刚度Cr=41400; %%后轮胎侧偏刚度Iz=3746; %%质心绕z轴的转动惯量Vx=5;%% 二自由度状态空间方程矩阵 %%a11=0;a12=1;a13=0;a14=0;a21=0;a22=-2*(Cf+Cr)/(M*Vx);a23=2*(Cf+Cr)/M;a24=-2*(a*Cf-b*Cr)/M*Vx;a31=0;a32=0;a33=0;a34=1;a41=0;a42=-2*(a*Cf-b*Cr)/(Vx*Iz);a43=2*(a*Cf-b*Cr)/Iz;a44=-2*(a*a*Cf+b*b*Cr)/(Vx*Iz);b1_1=0;b1_2=2*Cf/M;b1_3=0;b1_4=(a*Cf)/Iz;A=[a11 a12 a13 a14; a21 a22 a23 a24; a31 a32 a33 a34; a41 a42 a43 a44];B1=[b1_1;b1_2;b1_3;b1_4];%%%设置Q,R矩阵%%Q = [1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];%Q调大,误差会减小R = [100];%R调大,输入会减小%%%利用lqr函数求解K值 %%[K,P,r] = lqr(A,B1,Q,R);
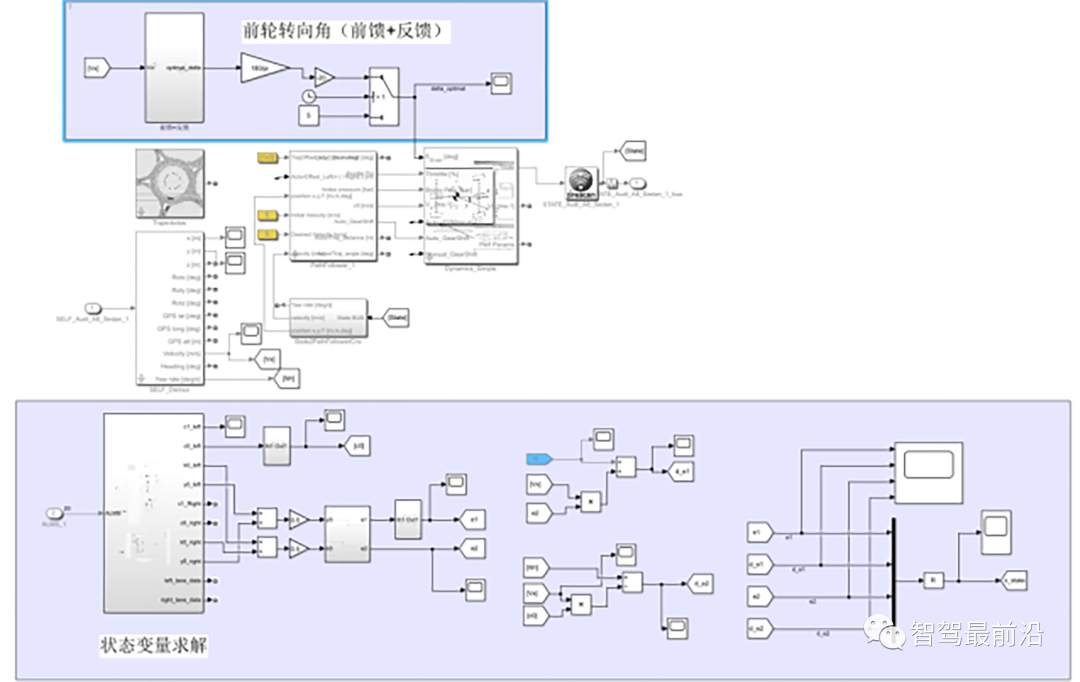
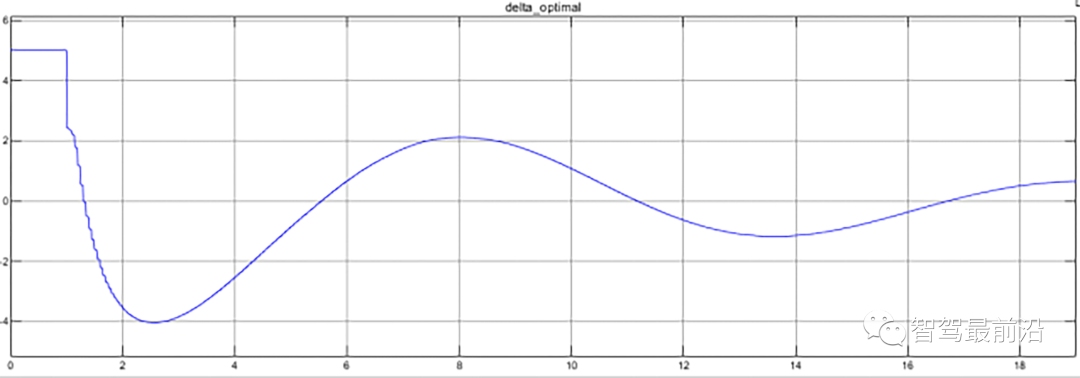
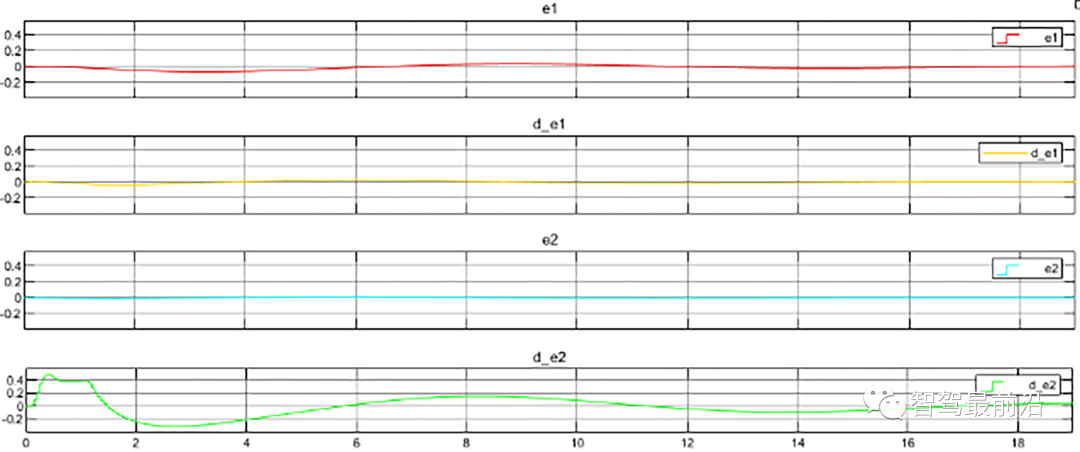
因此,简单的车道保持辅助系统已搭建完成,搭建控制器的Simulink程序框图如下所示:为体现LKA的控制效果,在仿真的初始时刻模拟驾驶员的误操作,给系统添加一个5°的前轮转角输入让车辆发生偏航,车辆逐渐偏离车道中心线,然后LKA系统介入。经过前馈+反馈的控制策略,使汽车保持在道路中心行驶。系统的仿真结果如下图所示:转载自智能运载装备研究所,文中观点仅供分享交流,不代表本公众号立场,如涉及版权等问题,请您告知,我们将及时处理。
-- END --
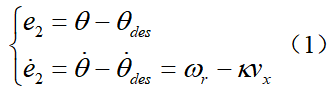
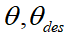 分别为实际的航向角与期望的航向角。横向误差变化率为
分别为实际的航向角与期望的航向角。横向误差变化率为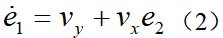
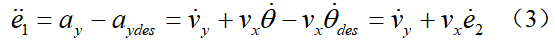
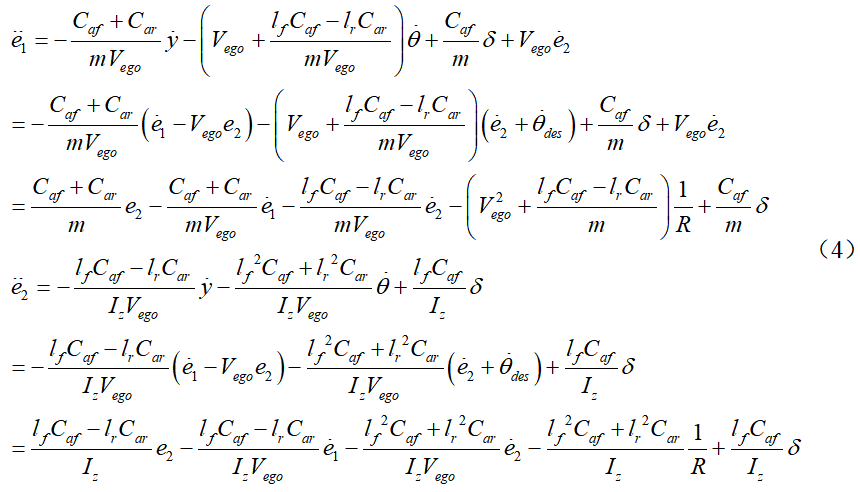
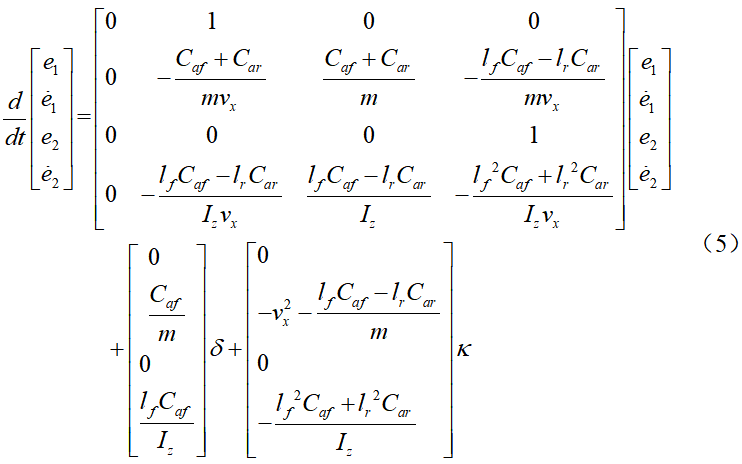
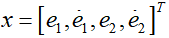 ,则车辆横向动力学模型写成状态空间形式为:
,则车辆横向动力学模型写成状态空间形式为: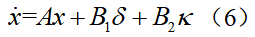
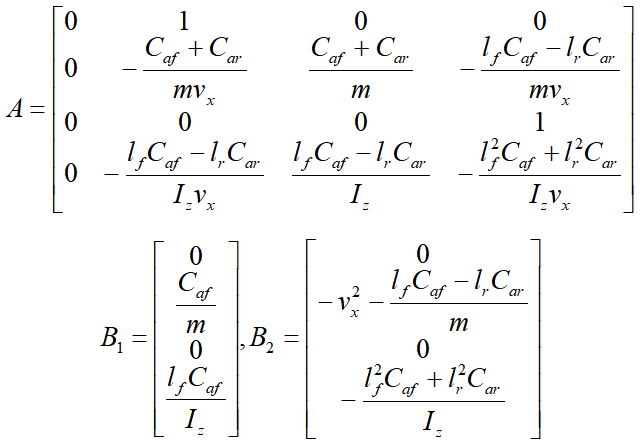
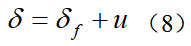
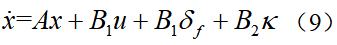
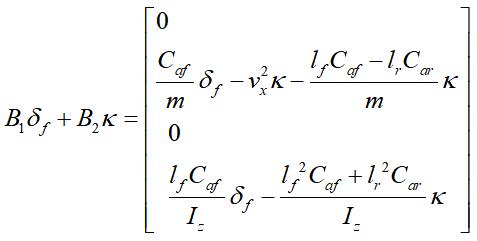
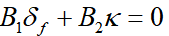
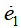 的前馈偏差为0,可得
的前馈偏差为0,可得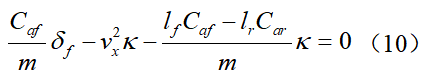
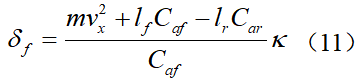
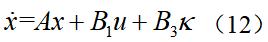
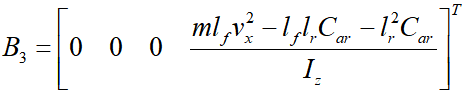
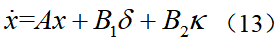
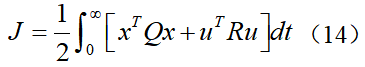
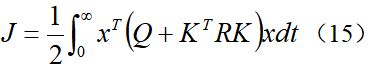
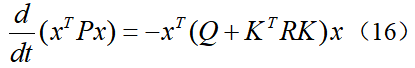
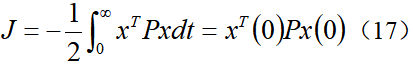
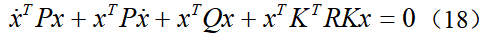
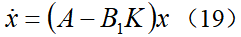
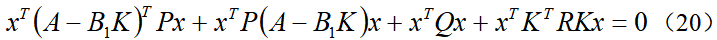
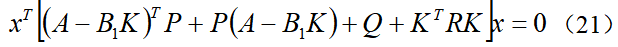
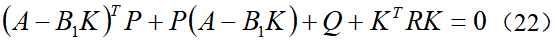
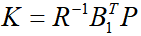 ,代入并整理可得黎卡提方程
,代入并整理可得黎卡提方程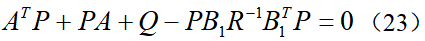
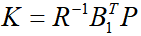 ,即得最优控制输入为u=-Kx。
,即得最优控制输入为u=-Kx。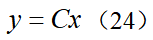
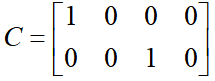
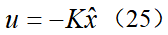
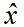 为系统状态x的估计值。
为系统状态x的估计值。



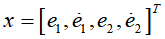 ,即:
,即: