【半导光电】重磅！芯片滤波器设计实战指南

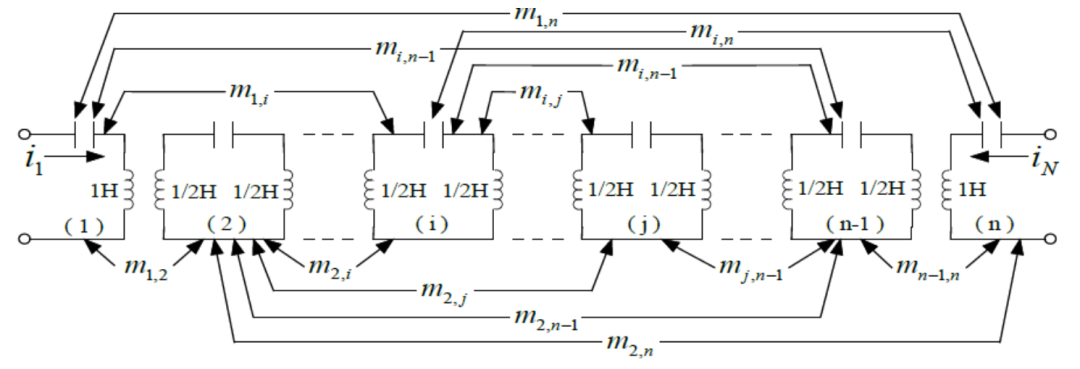耦合型滤波器的低通原型电路

针对上图中的耦合型滤波网络，假设不存在传输损耗，此时上面的散射参数矩阵可以得到如下公式：

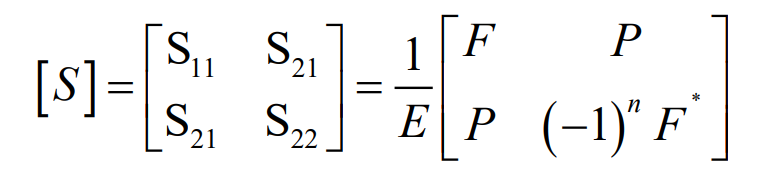
其中，n是谐振器个数。E、P和F是以为复变量的多项式，ω0是归一化频率。

此时滤波器的传输系数：

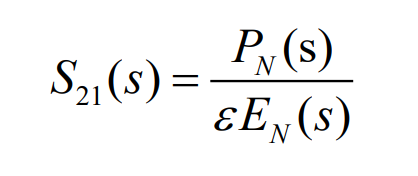
其中PN(S)是以ｓ为变量的m阶多项式（m使传输系数为零的频率点被称作滤波器的传输零点。ε是在ω=±1归一化的常数：

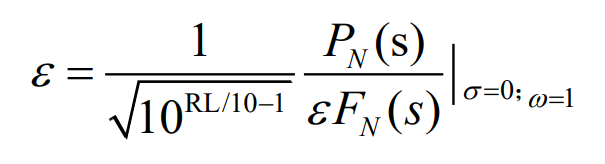
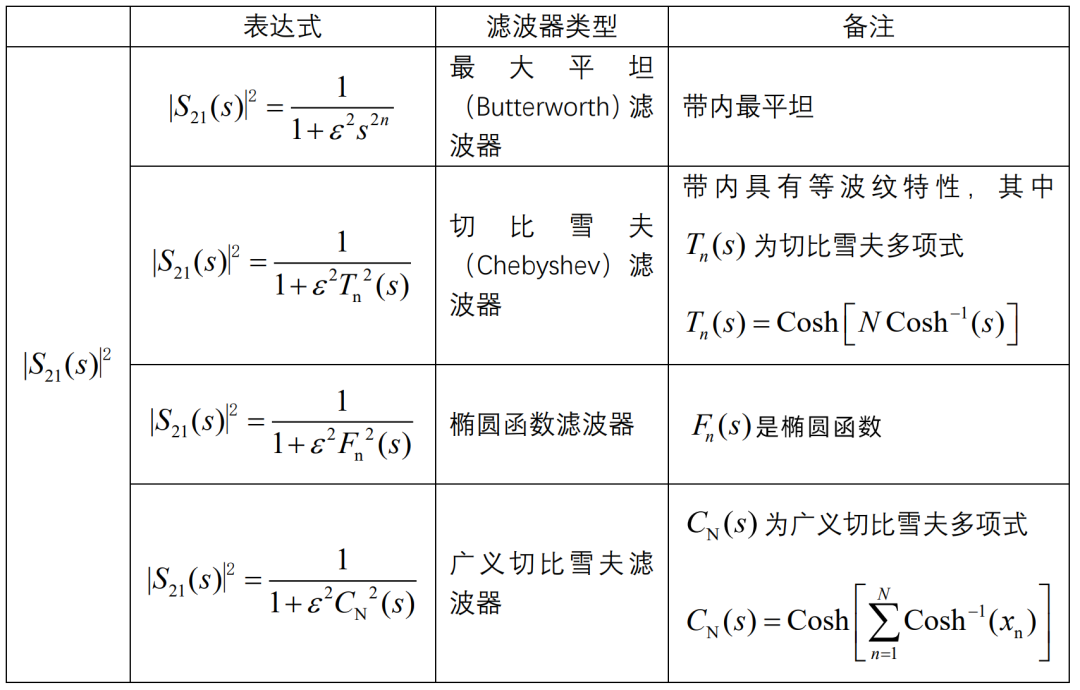
其中RL表示滤波器的回波损耗（Retrun Loss）。上文提到的按照响应函数对滤波器分类下表给出了常见的传输函数S21的分类：

表1 常见滤波器传输函数及滤波器分类

同理，由上面的散射矩阵可得反射系数为：

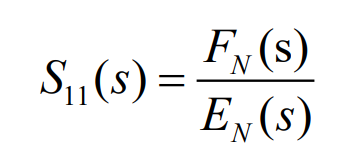
其中FN是n阶首项为1的多项式，EN是归一化Hurwitz多项式。并满足下面的谱方程：

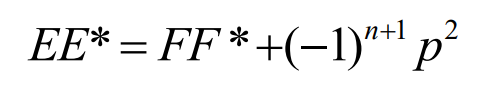
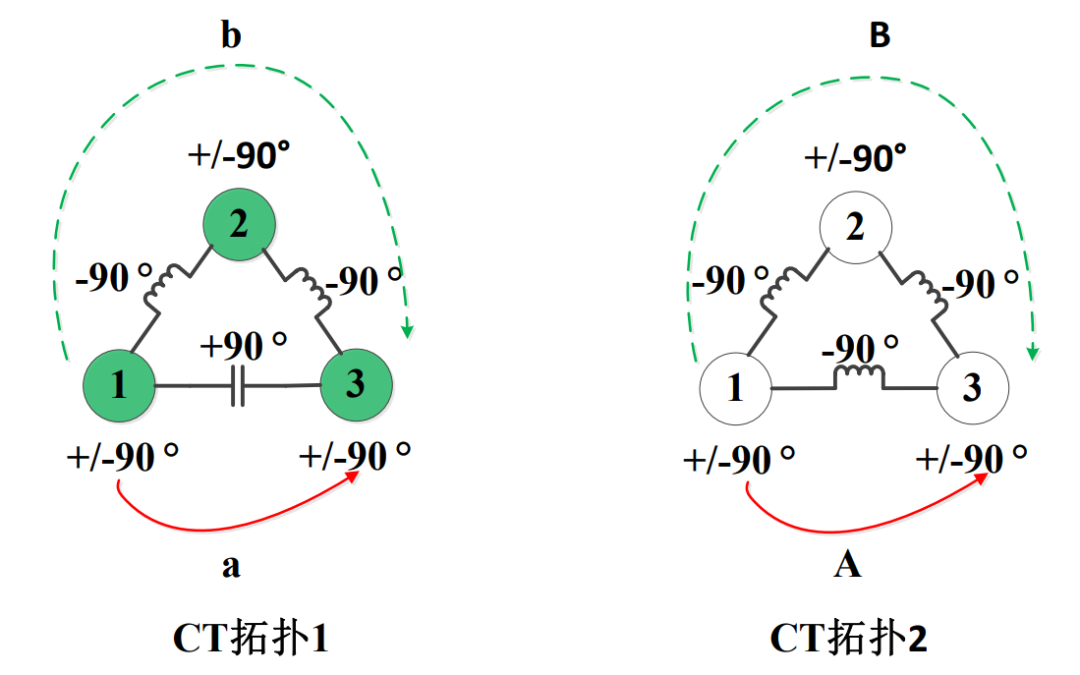
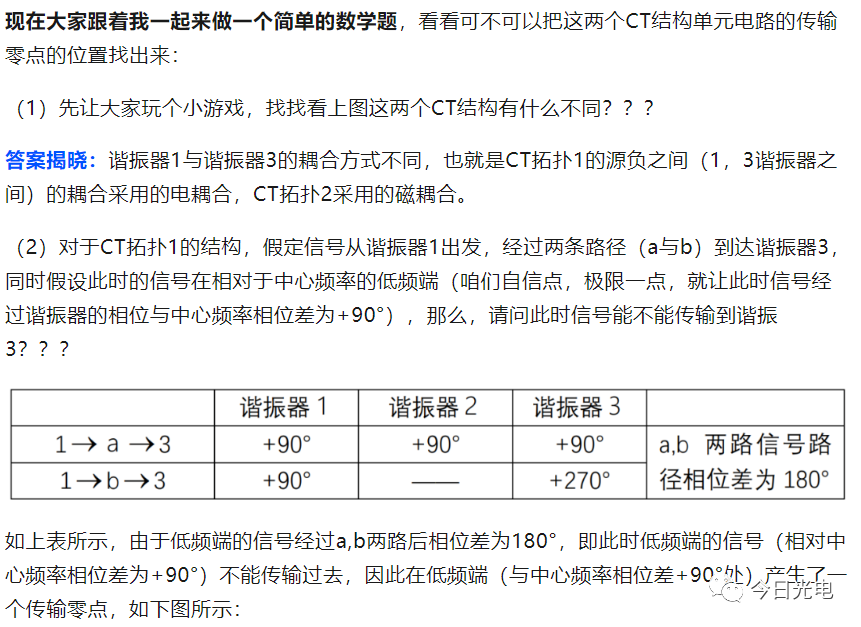
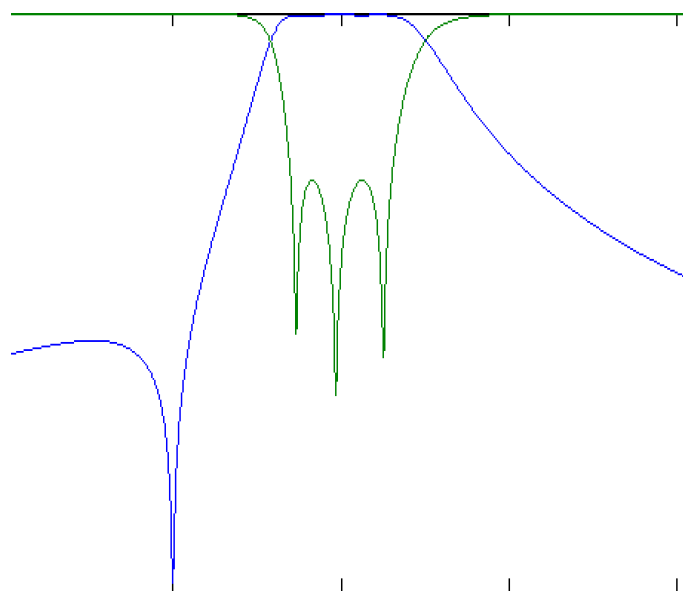
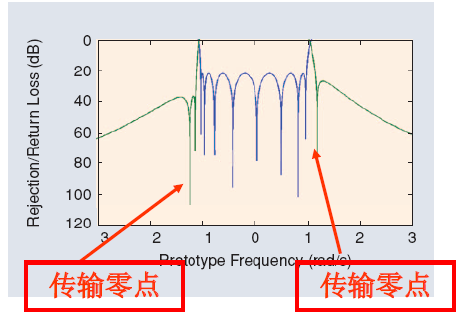
（3）同样的道理，CT拓扑2的高频端信号（与中心频率相位差-90°），由1→A→3与1→B→3两条路径也不能由谐振器1传输到谐振器3，因此CT拓扑2的耦合矩阵得到的滤波器能够在高频端获得一个传输零点，如下图所示：

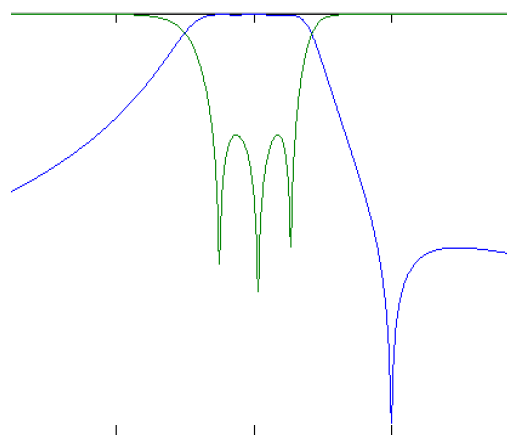
对于引入了两个传输零点的CQ结构，也可以按照此类方法分析。由于CQ结构的组合较多，本文先给出如下图所示的一个CQ拓扑结构的传输相位关系的数学推导（其余的CQ拓扑的数学推导，大家可以自行下来算算哦）：

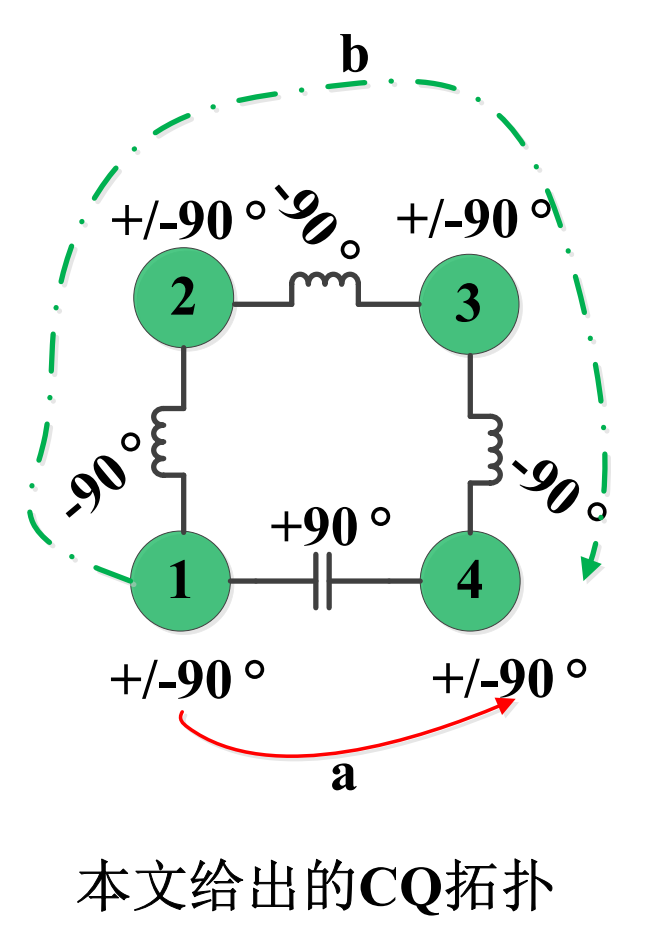
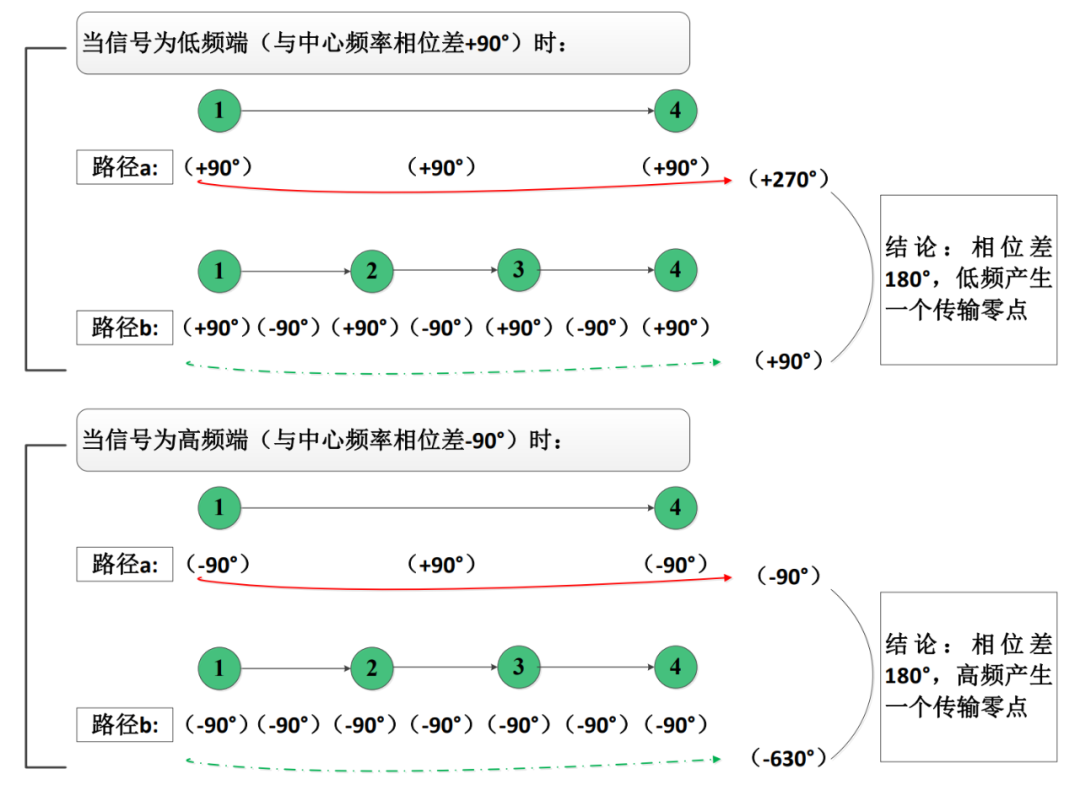
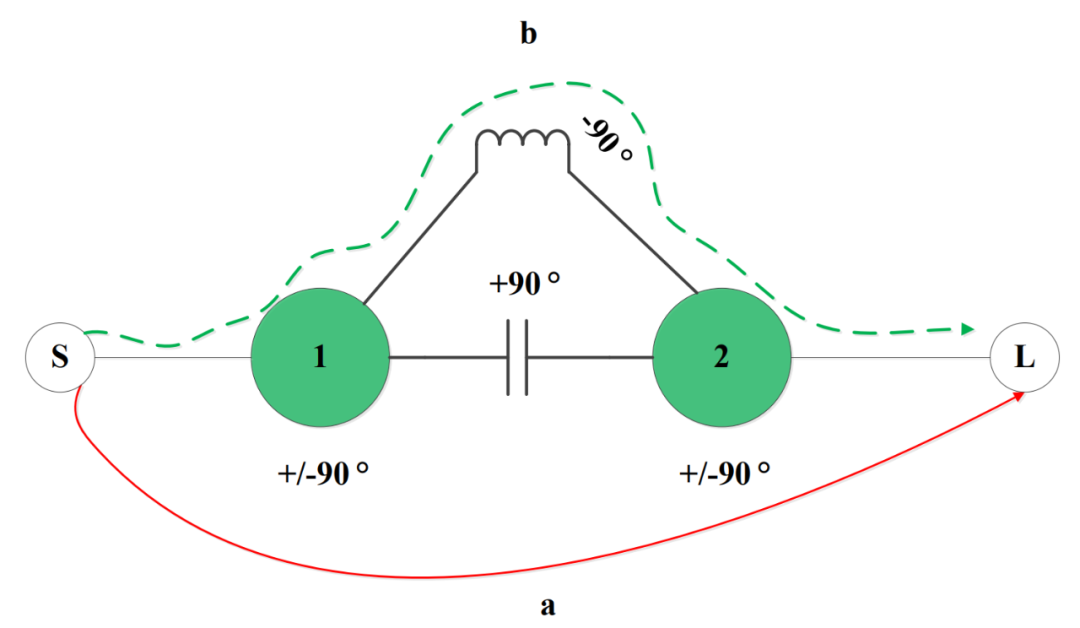
此时根据设计指标，利用耦合矩阵综合软件（可以是之前RFASK的博主分享的也可以自己在Matlab里面编写）建立上图拓扑，然后得到耦合矩阵以及原型响应曲线如下：

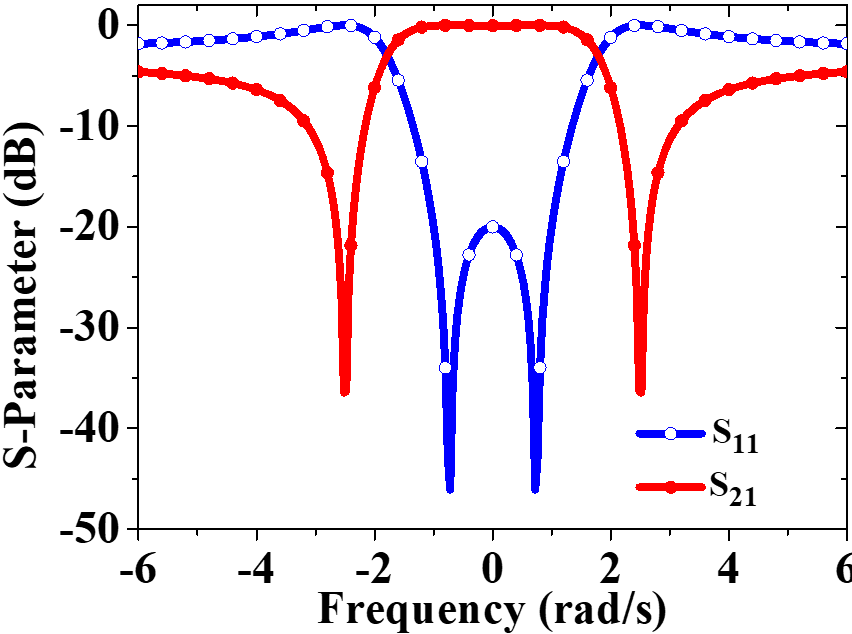
——滤波器原理图设置以及仿真：

根据综合得到的耦合矩阵，然后计算得到谐振器以及耦合之路的电感电容值，具体的推导不在赘述，下面给出本文中的理论方法：

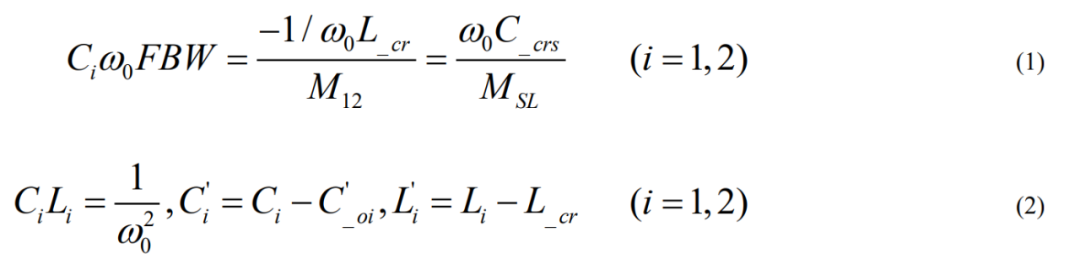
此时

其中Y0为1/50Ω^-1，Ci为自定义的归一化电容值。然后在ADS2022中搭建原理图仿真得到如下结果：

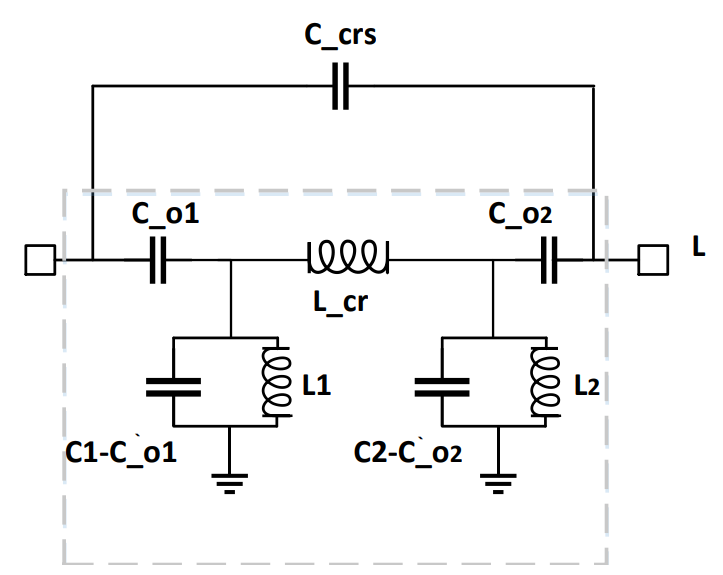
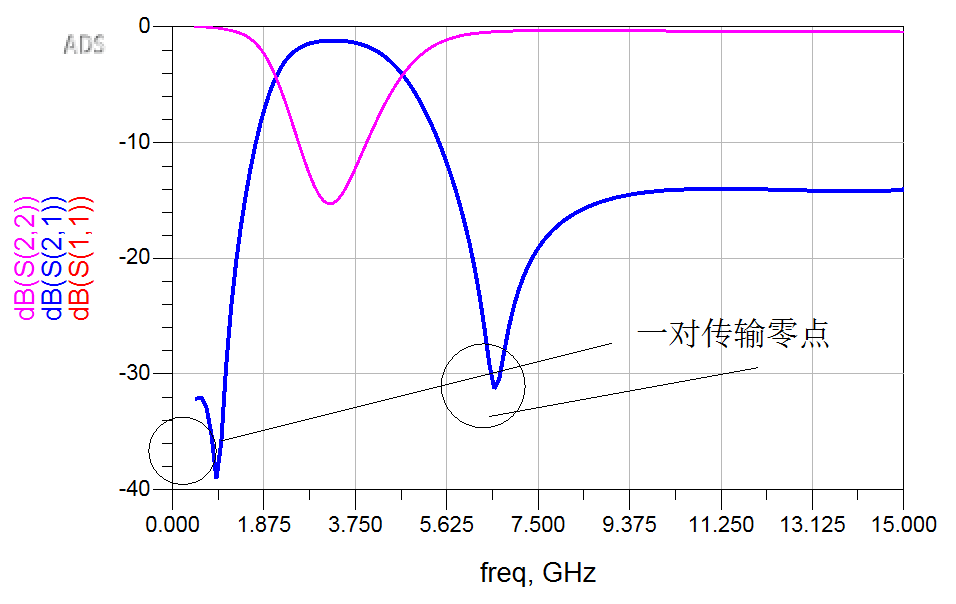
上图基本实现了一对传输零点的引入，下面再在ADS Momentum中搭建电磁仿真模型。

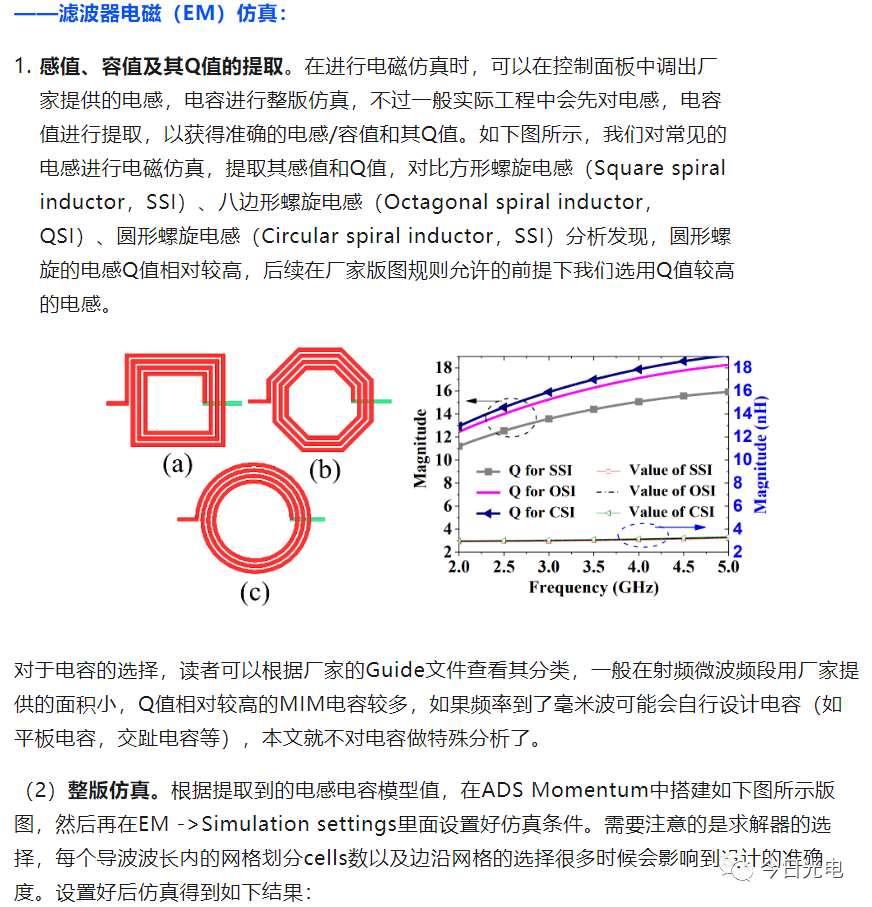
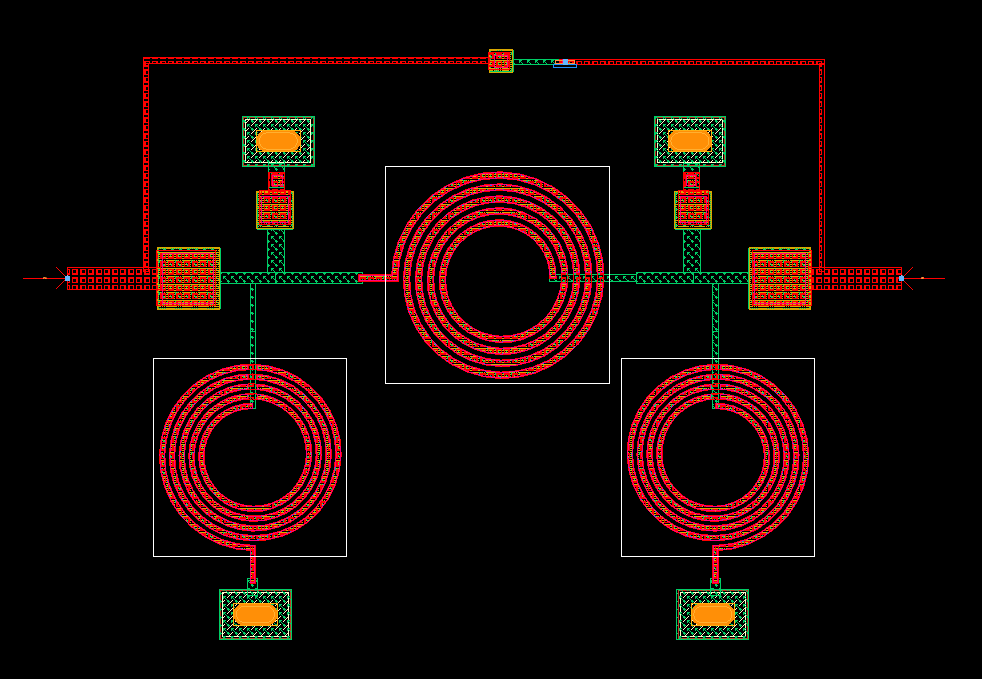
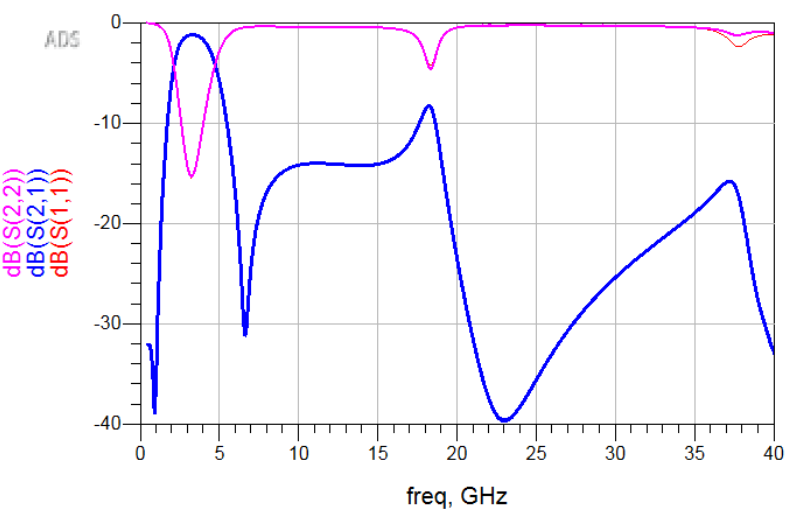
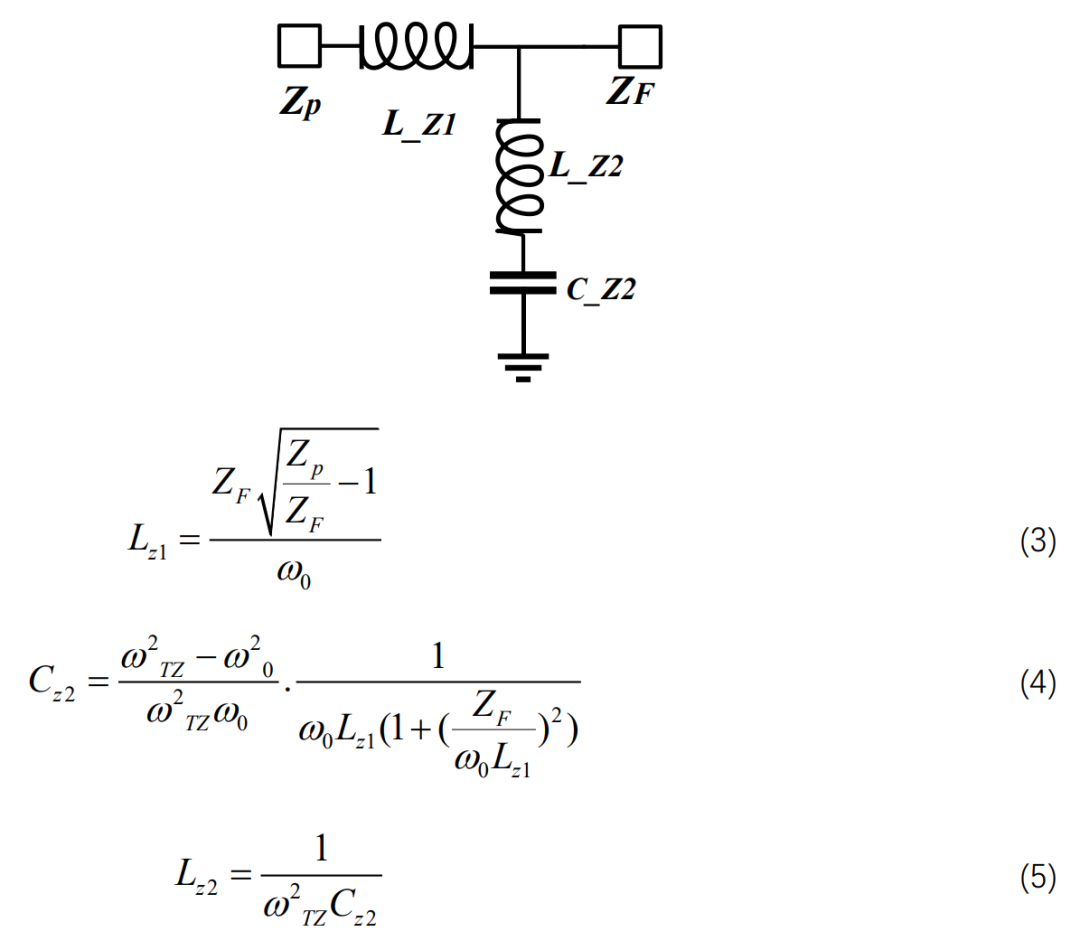
其中，fTZ = 10 GHz, f0 = 3 GHz, ZF = 50 Ω and ZP = 82 Ω（Zp是对上文版图的输出端口阻抗提取得到的值）那么可以推导出对芯片进行重新绘制电磁仿真模型，得到如下仿真结果

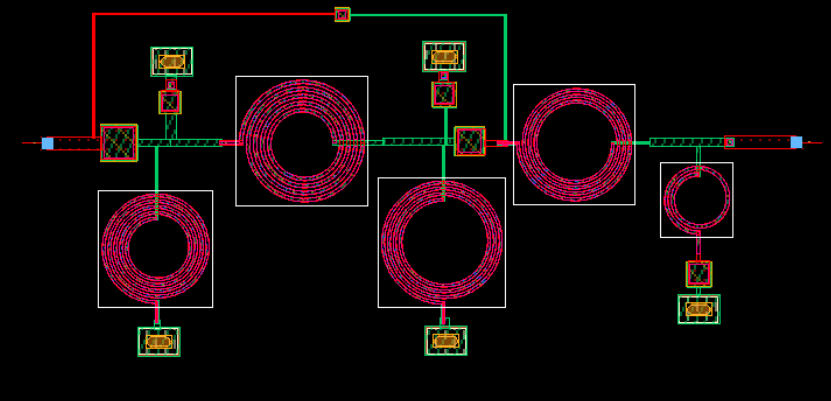
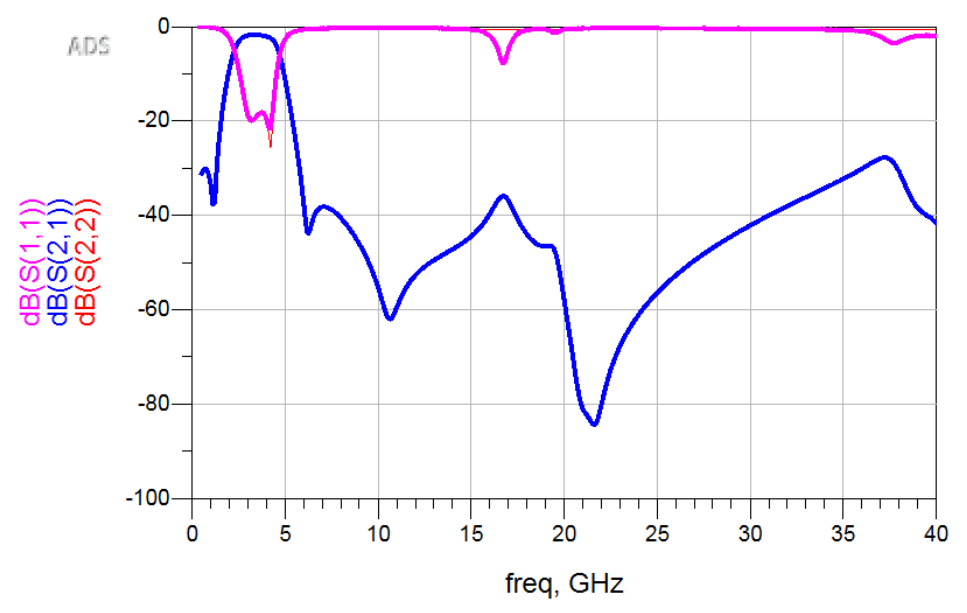
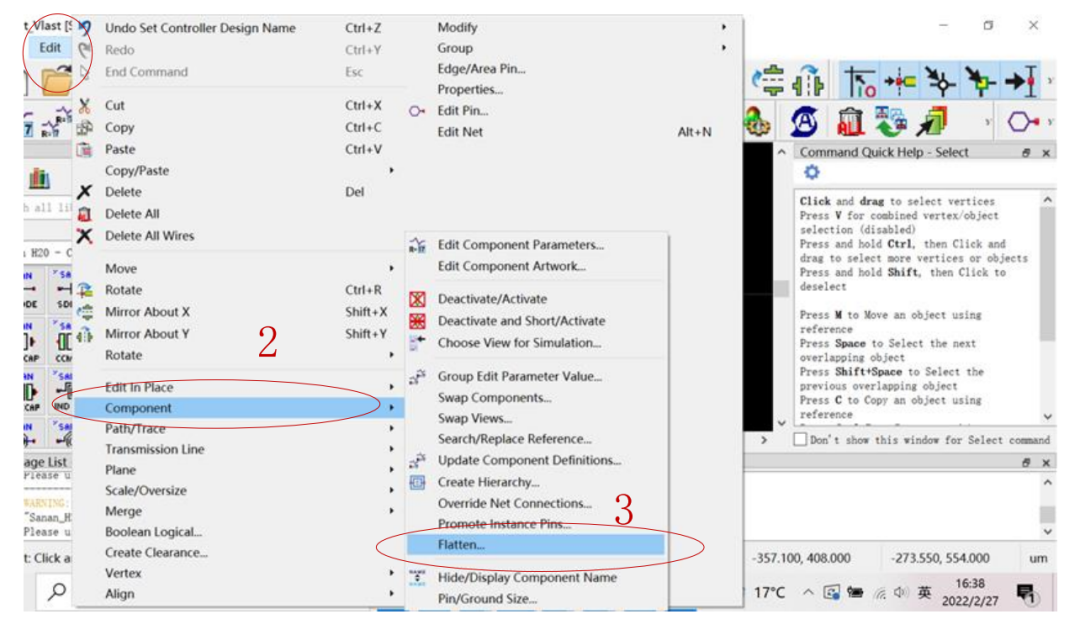
——END——

后记：滤波器的理论要求相对较高，本文涉及不及万分之一，仅仅展示了一种相对容易的数学方法结合仿真软件来实现芯片滤波器的设计，前前后后码字到眼花，仓促之间难免有纰漏，希望各位兄弟姐妹能积极讨论修正哦。

----与智者为伍 为创新赋能----

投稿丨合作丨咨询

联系邮箱：uestcwxd@126.com

QQ：493826566