
(1) ◎ 解答:
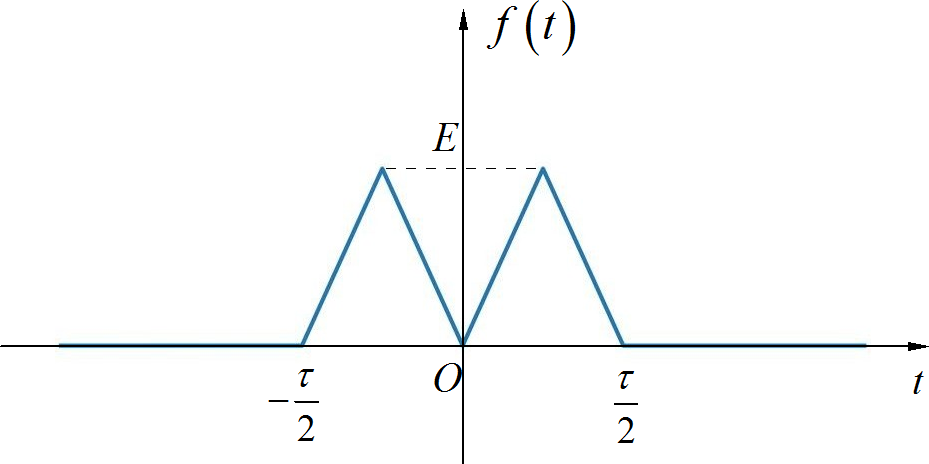
▲ 图1.1.1 双三角脉冲信号□ 解法(1):使用微分性质求解
将 进行两次微分,得到四个冲激信号, 如下图所示:
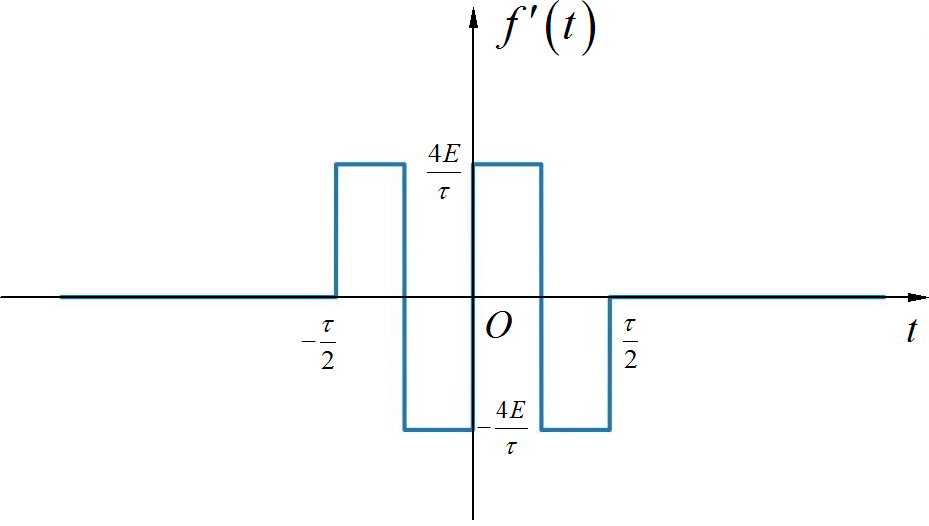
▲ 图1.1.2 信号的一阶导数
▲ 图1.1.3 信号的二阶导数根据信号二阶导数,可以写出对应的二阶导数的傅里叶变换:
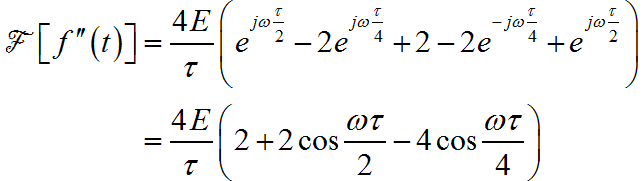
那么,信号的频谱为:
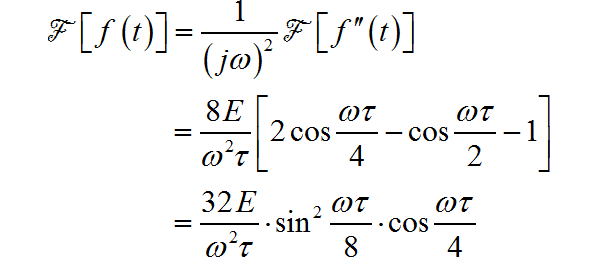
□ 解法(2):使用卷积方法
信号 可以拆解成两个信号的卷积 。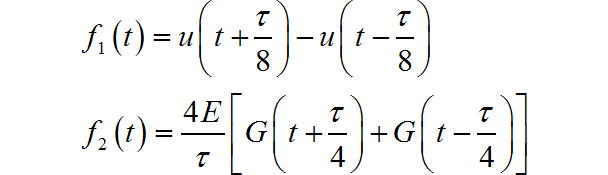
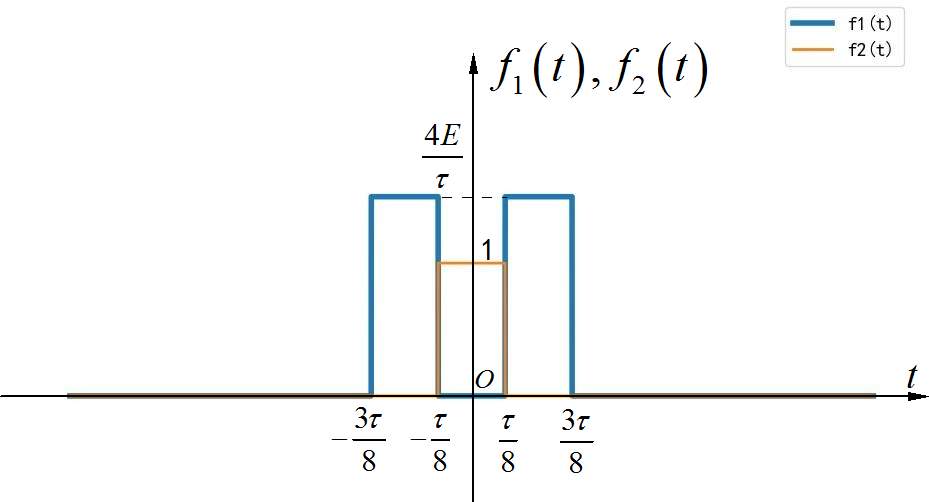
▲ 图1.1.4 拆解成两个矩形信号的卷积这两个信号的频谱分别是:
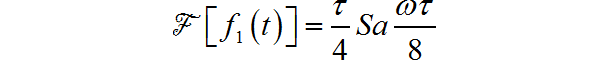
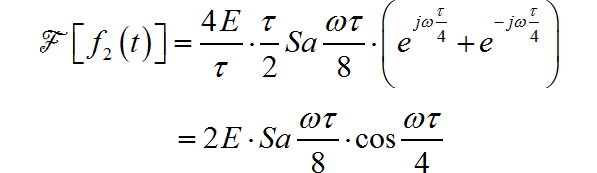
那么, 根据傅里叶变换卷积定理,信号的频谱等于这两个信号频谱的乘积:
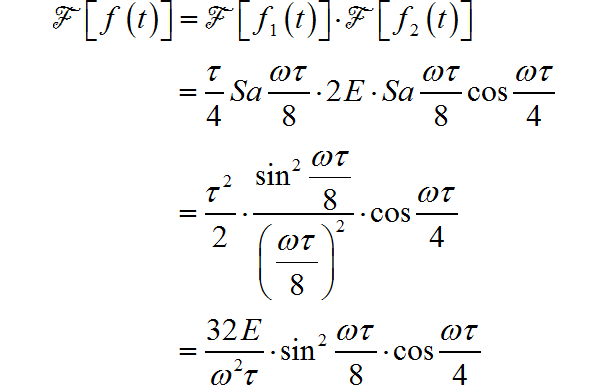
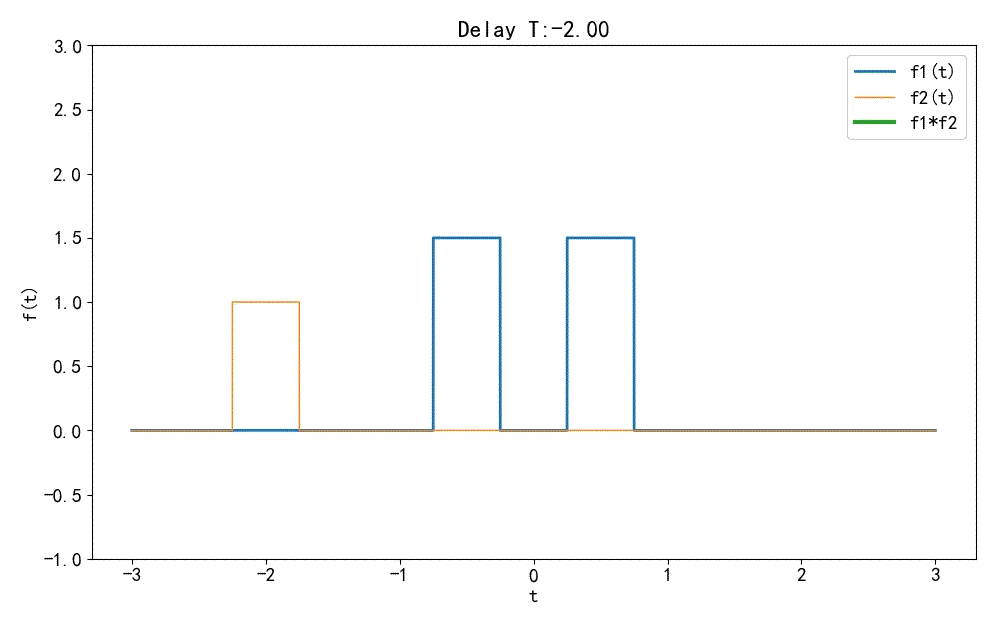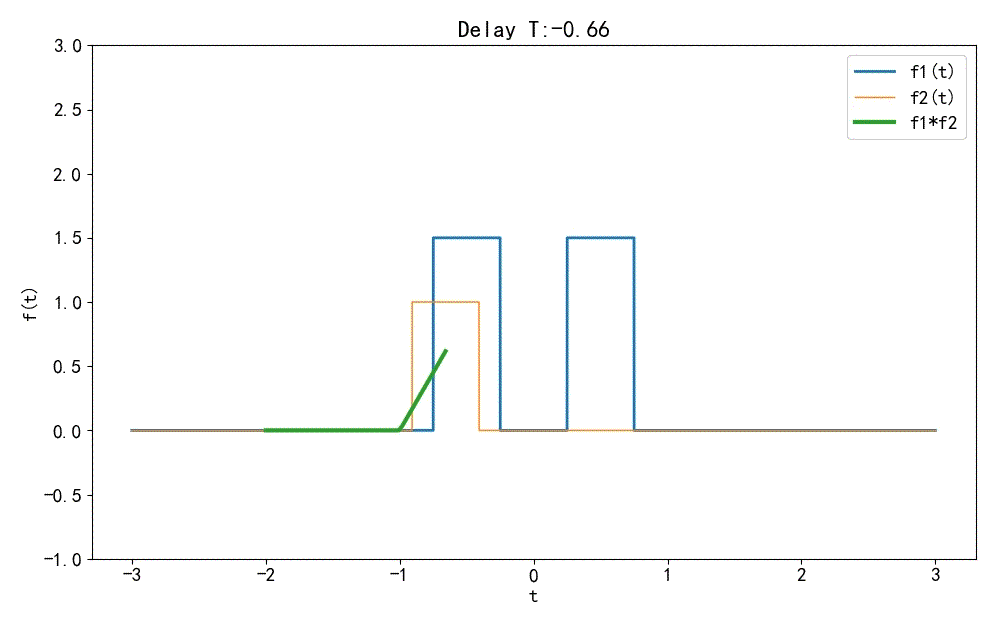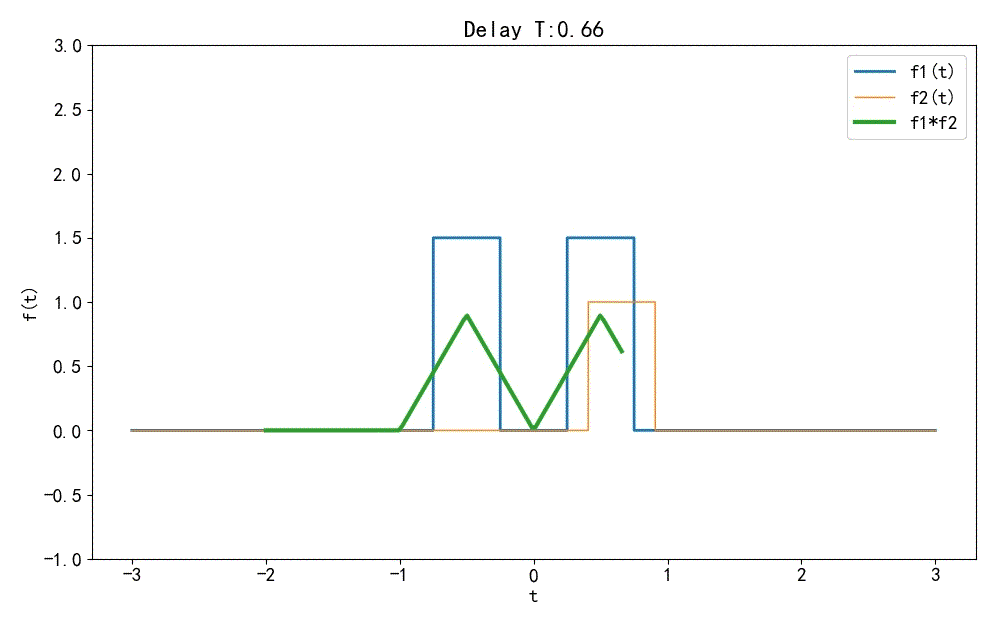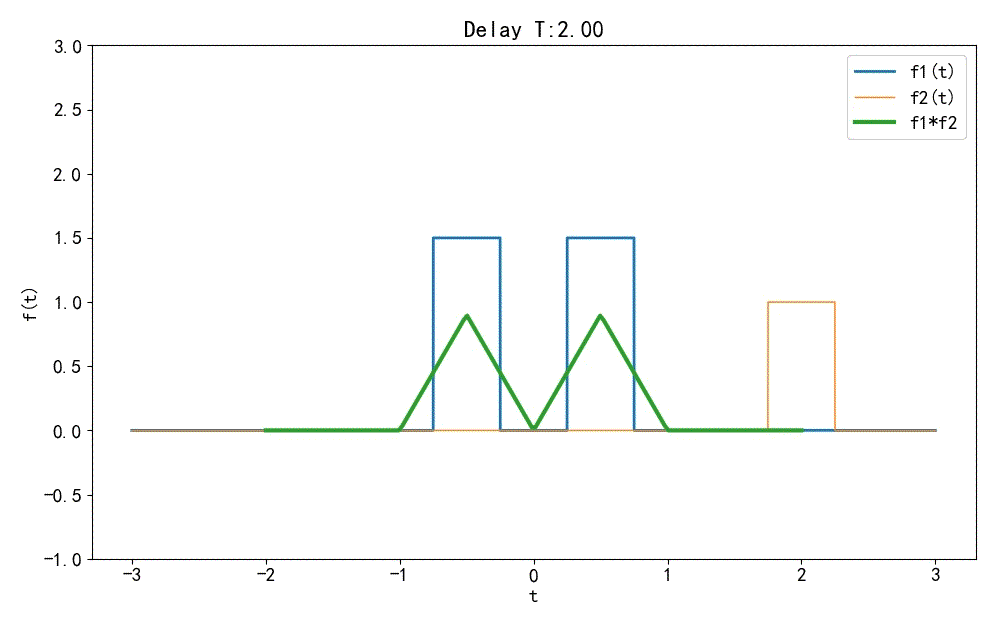
▲ 图1.1.5 两个信号卷积过程(2) ◎ 解答:
根据傅里叶变换频域微分定理,可以知道:
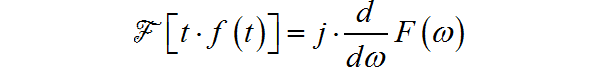
再根据福利变换时移特性:
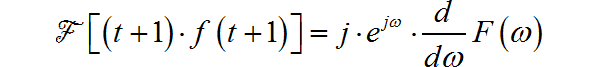
再根据傅里叶变换尺度特性:
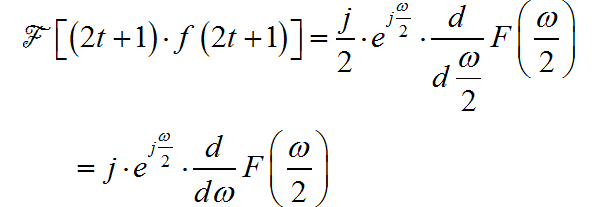
对给定的信号进行拆分,形成两部分:
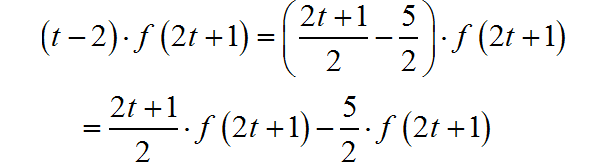
前面一部分对应的傅里叶变换,通过前面推导可以求出。后面一部分对应的频谱,根据傅里叶变换的线性、尺度、时移特性可以求得:
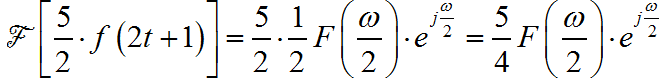
因此,整体信号傅里叶变换为:
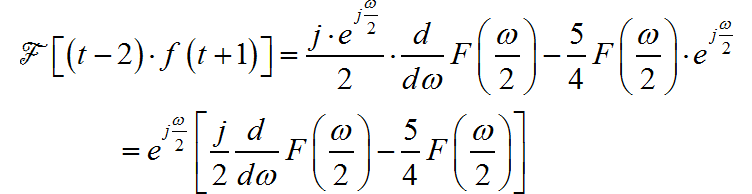
(3) ◎ 求解:
根据福利变换中的时域微分定理: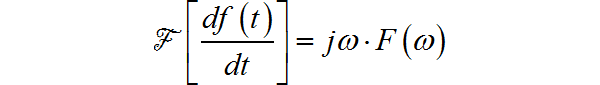
再根据傅里叶变换中的频域积分定理:
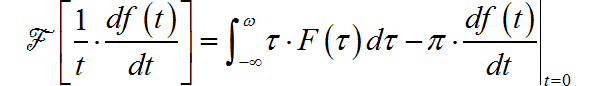
(4) ◎ 解答:
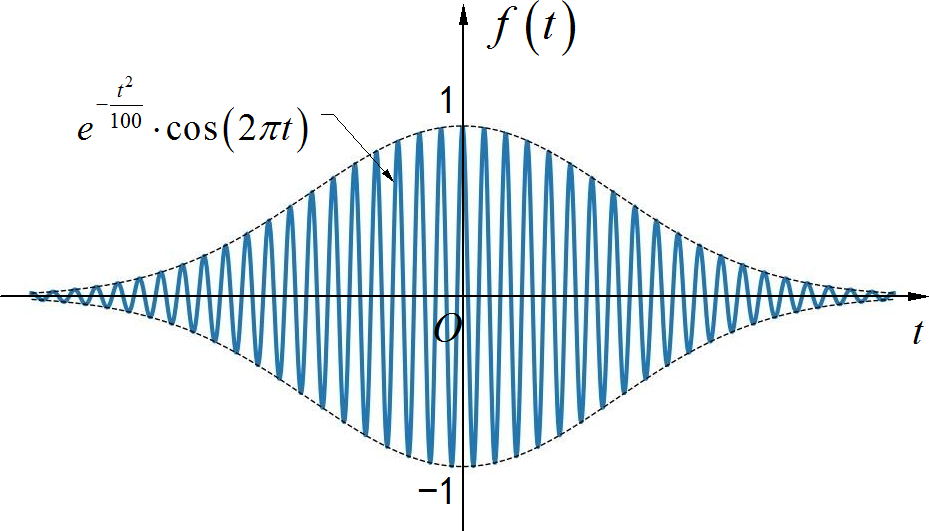
▲ 图1.1.6 调制的高斯信号根据高斯信号的频谱公式,可以知道题目中高斯信号对应的傅里叶变换为:
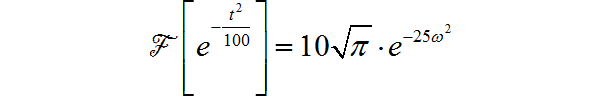
在根据傅里叶变换的频移特性,对于调制高斯信号的频谱为:
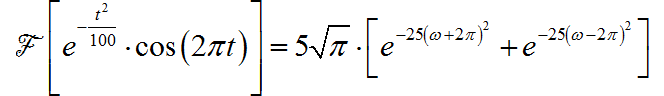 (5) ◎ 解答:
(5) ◎ 解答:
在单边指数信号的频谱的基础上,分表应用傅里叶变换的频域微分定理,平移定理,可以得到信号的频谱。
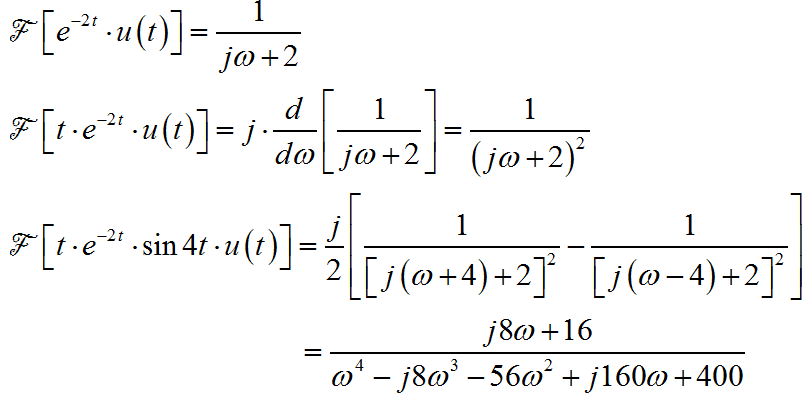
(6) ◎ 解答:
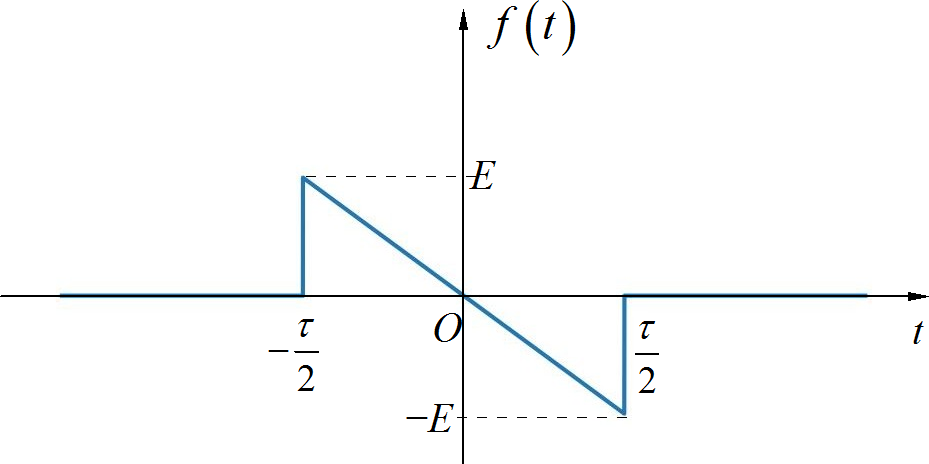
▲ 图1.1.7 锯齿脉冲信号对信号进行求导, 如下图所示。它对应的频谱为:
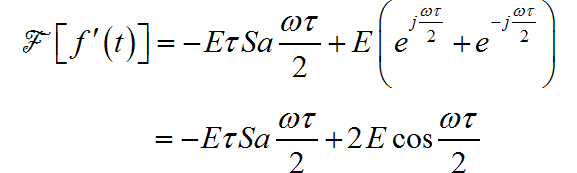
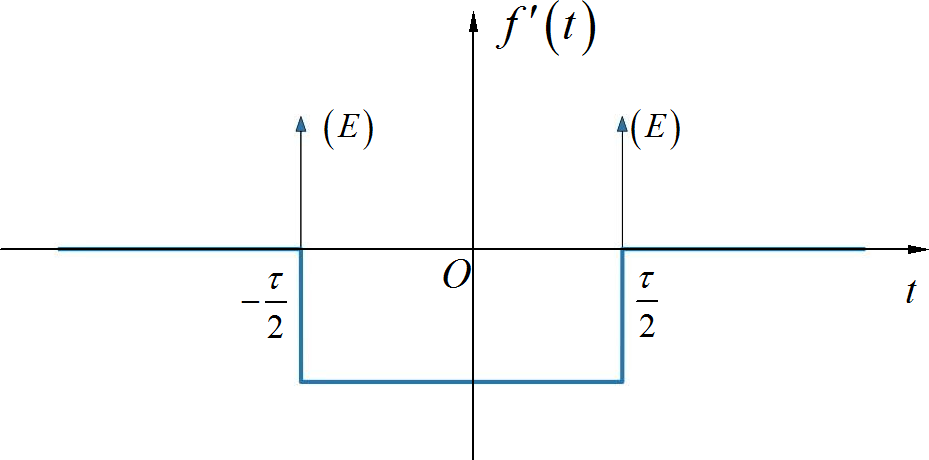
▲ 图1.1.8 信号的导数波形再利用傅里叶变换的积分定理,可以求出信号的频谱为:
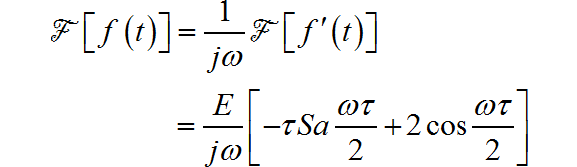
由于信号为奇对称信号, 所以 。
(7) ◎ 解答:
信号可以看成一个窗口信号与 的乘积。

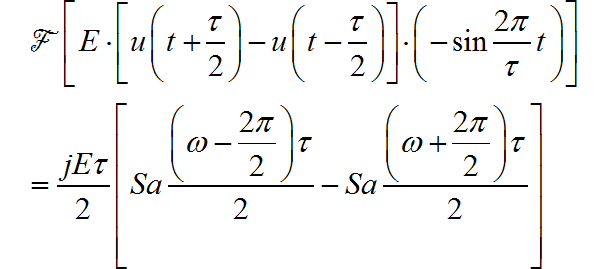
(8) ◎ 解答:
根据傅里叶变换对偶定理,可以知道:
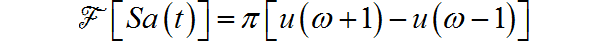
根据傅里叶变换频域微分定理:
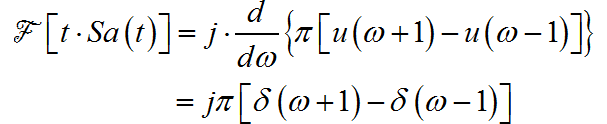
根据傅里叶变换的平移定理: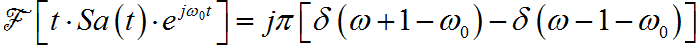
最终,信号的频谱为:
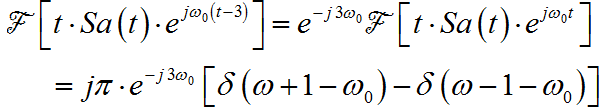
(9) ◎ 解答:
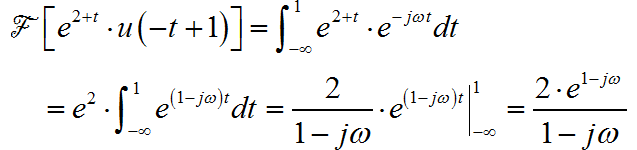
(1) ◎ 解答:
符号函数 的频谱为:
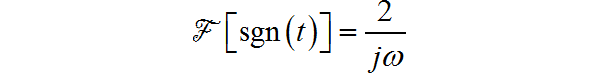
根据频域微分定理:
 所以:
所以:
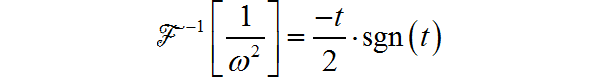 (2) ◎ 解答:
(2) ◎ 解答:
已知单边衰减指数的频谱公式:
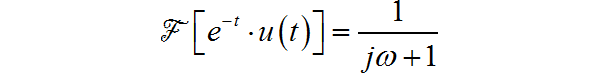
根据傅里叶变换的尺度特性:
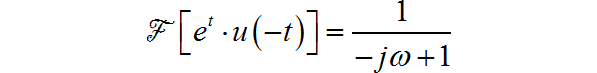
所以: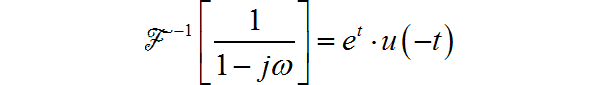 (3) ◎ 求解:
(3) ◎ 求解:
在频谱中包含有两种频谱,一是 , 另外一个是两个矩形频谱。
对于冲激频谱,对应的傅里叶反变换为:
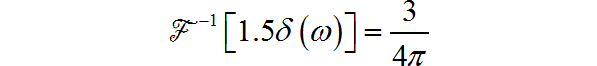
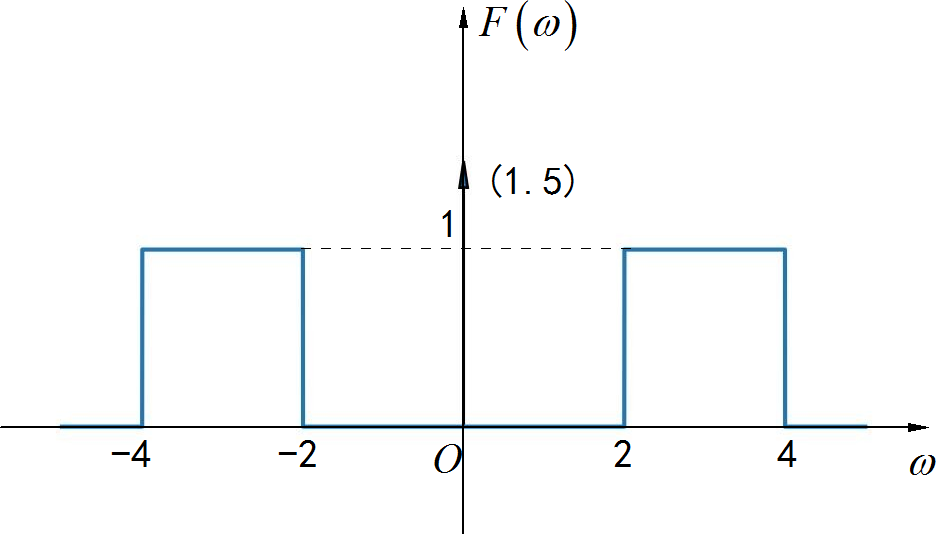
▲ 图1.1.9 信号的频谱对于两个矩形频谱,可以看成由中心在 0 点的矩形频谱,左右搬移形成, 这个过程可以描述为时域信号乘以 。根据傅里叶变换对偶特性,求单个矩形频谱对应的时域信号。
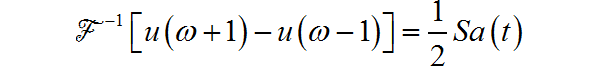
乘以 之后,便形成左右两个矩形频谱。最终,信号 为:
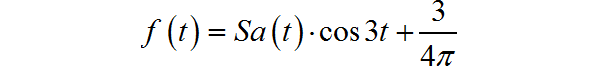
◎ 求解:
根据傅里叶变换频域卷积定理, 对应的频谱为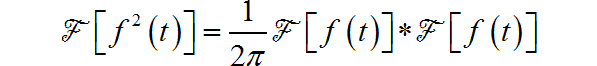
根据 的表达式,可以将其拆解成两个成份:
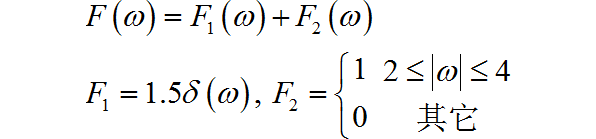 的波形如下所示:
的波形如下所示:
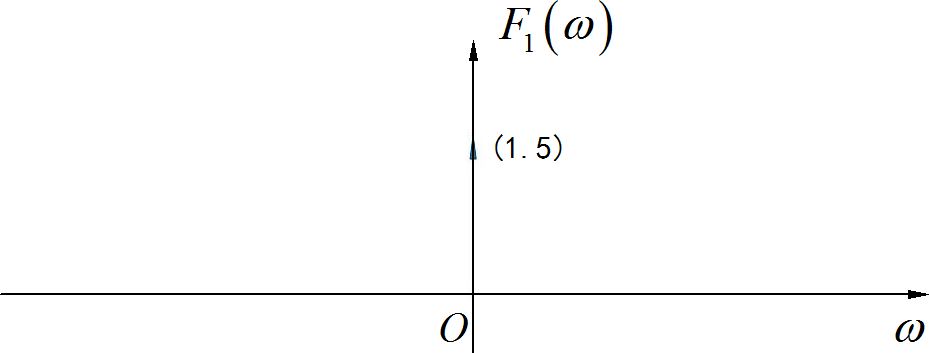
▲ 图A1.1.10 F1(omega)的波形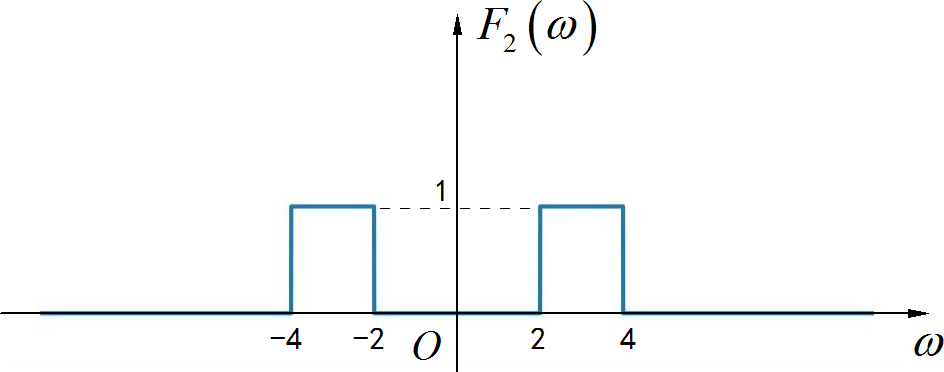
▲ 图1.1.10 F2(omega)的波形根据卷积代数性质, 可以将 与 的卷积拆解成三项:
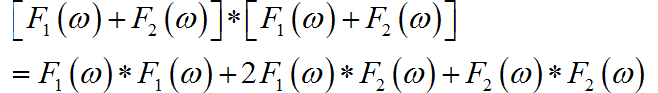
下面分别绘制出上面三项的卷积结果:
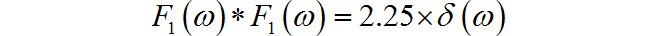
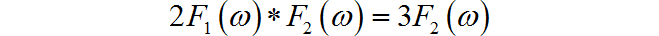
的波形如下:
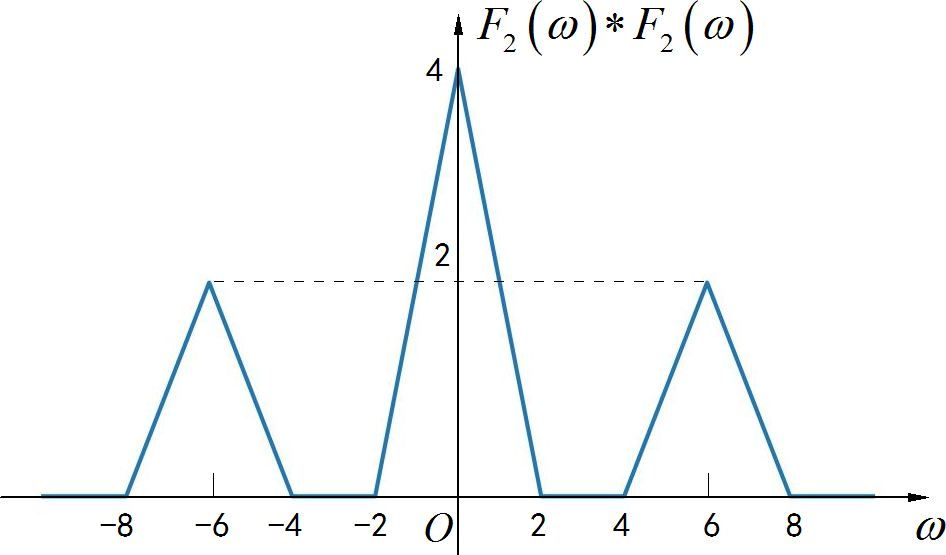
▲ 图1.1.11 F2(omega)与自身的卷积将上面三个频谱叠加在一起:
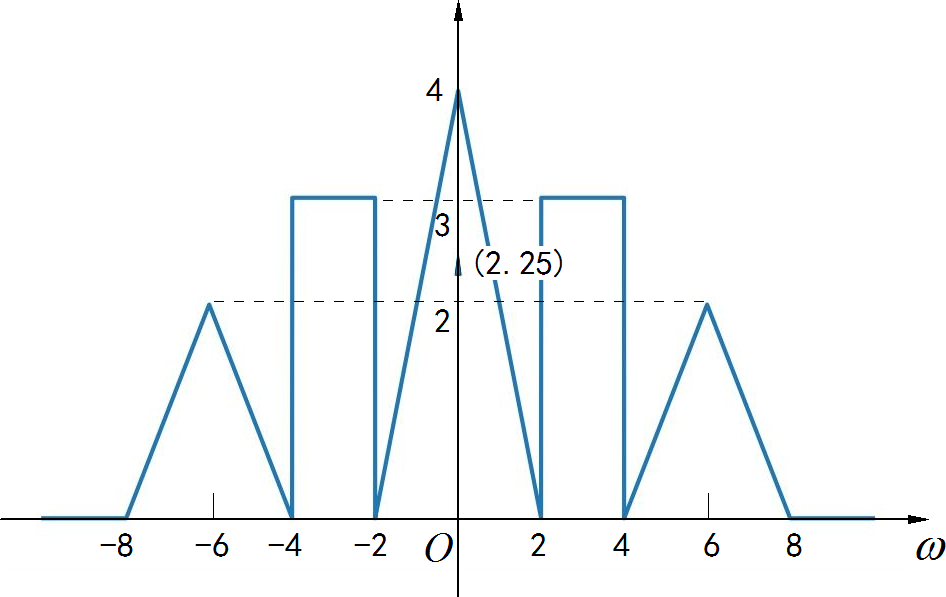
▲ 图1.1.13 三个频谱成分叠加在一起最后再把上面频谱除以 ,最终频谱为:
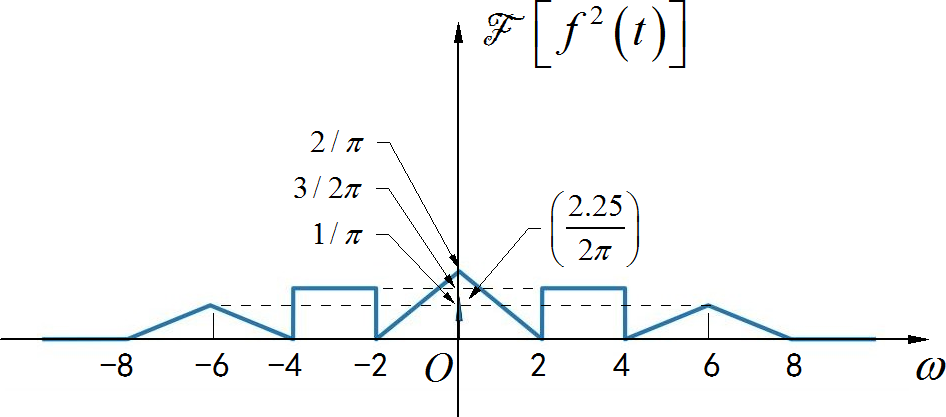
▲ 图1.1.14 最终f(t)平方的频谱(1) ◎ 解答:
信号的周期为 ,对应的角频率为 。周期信号的频谱是将单个周期信号的的频谱进行离散化。
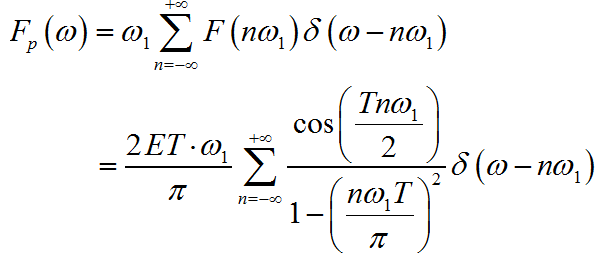
(2) ◎ 解答:
信号可以看成一个三角脉冲信号 与一个周期三角脉冲信号 的乘积: 。根据傅里叶变换频域卷积定义可知:
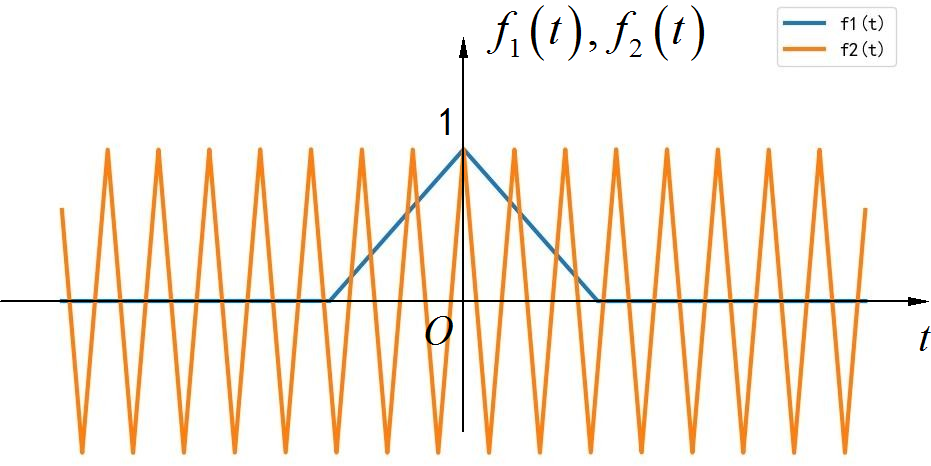
▲ 图1.2.1 f1(t),f2(t)的波形三角信号的频谱为:
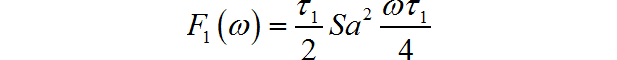
周期三角信号可以看成下面窄的三角信号周期延拓, 再减去 1。
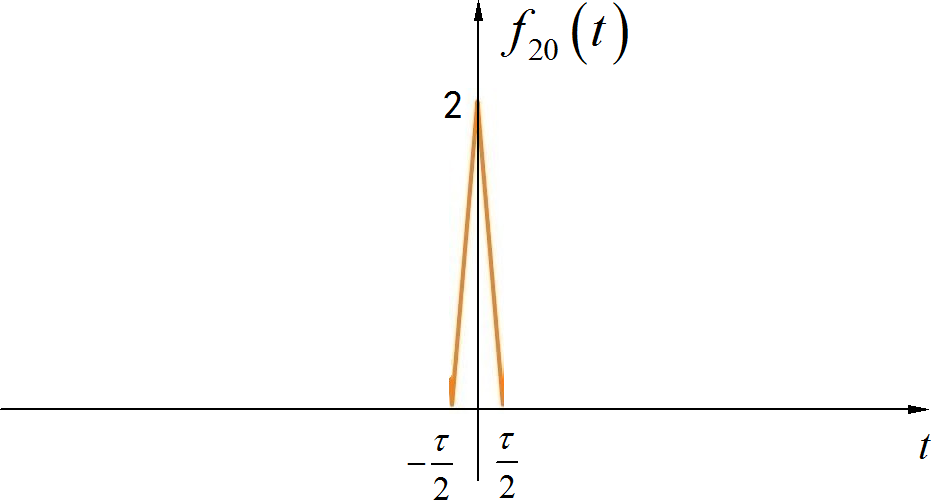
▲ 图1.2.2 单个三角脉冲单个窄三角信号的频谱为:
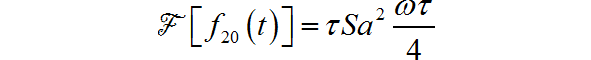
那么周期三角信号的频谱是对上述信号进行离散化,后面需要减去常量 1 的频谱:

计算 的卷积: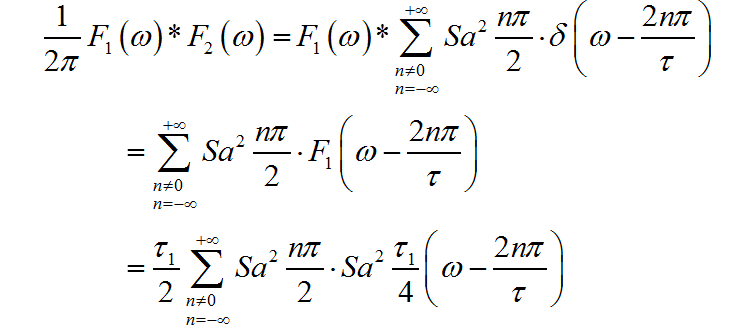
(3) ◎ 解答: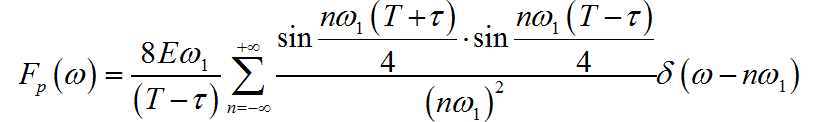
◎ 证明:
根据希尔伯特变换 的定义,有:
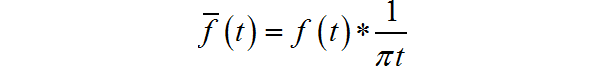
根据傅里叶变换卷积定理,
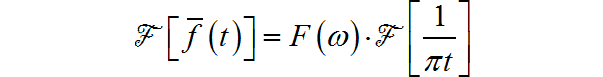
下面求 的傅里叶变换。根据
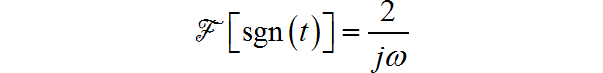
根据傅里叶变换的对偶特性,
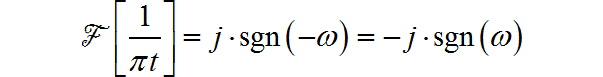
因此
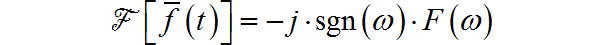
再由 ,可得,
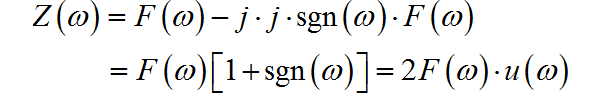
信号与系统 2023(春季) 作业要求 - 第七次作业: https://zhuoqing.blog.csdn.net/article/details/129986853