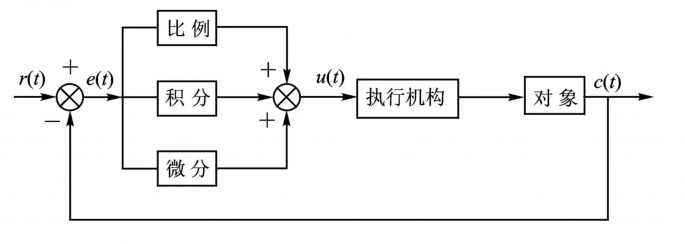
在学习 PID 算法的参数整定的时候,每一个系统的 PID系数是不通用的,在不同的系统中运用同样的 PID 系数,其最终所体现的效果可能是相差可能甚远的,所以我们需要根据实际的系统进行 PID 的参数整定(调参)。
采样周期选择
采样周期指的是 PID 控制中实际值的采样时间间隔,其越短,效果越趋于连续,但对硬件资源的占用也越高。在实际的应用中,我们可以使用理论或者经验方法来确定采样周期:
① 理论方法:香农采样定理。
这个定理可以用来确定采样周期可选择的最大值,当采样周期超出了这个最大的允许范围,我们所得到的信号就会失真,也就无法较好地还原信号了。
香农采样定理的具体原理我们不展开介绍,感兴趣的朋友可以去查找相关的资料,我们这里重点关注经验方法。
② 经验方法:根据控制对象突变能力选择。
假设电机当前转速为 20RPM,我们需要提高它的转速到 30RPM,此电机的转速在 1s 之内最大可以突变 10RPM,如果我们每 1ms 采集一次电机转速,那么每一次采集到的速度变化量最大为 10RPM / 1000 =0.01RPM。
很明显,此时最大的变化量远远小于当前的速度,对我们的 PID 控制效果并没有明显的提升,但是却占用了很多的硬件资源,因此,我们需要根据控制对象的突变能力来选择采样周期。
PID 参数整定方法

理论计算整定法:依据系统的数学模型,经过理论计算确定 PID 参数。
这种方法是建立在理想化条件下的,其得到的参数不一定能够直接使用,还需要结合经验以及实际的系统进行调整。
工程整定法:依靠工程经验,直接在控制系统的试验中进行整定,此方法易于掌握,在实际调参中被广泛采用。工程整定法包括:试凑法、临界比例法和一般调节法。
注意:无论采用哪一种方法所得到的 PID 参数,都需要在实际运行中进行最后调整与完善,因此,在 PID 参数整定中,最重要的就是经验的积累。**
① 比例系数:调节作用快,系统一出现偏差,调节器立即将偏差放大输出
② 积分系数:积分系数的调节会改变输入偏差对于系统输出的影响程度。积分系数越大,消除静差的时间越短,但是过大的积分系数则会导致系统出现超调现象,这在具有惯性的系统中尤为明显。
③ 微分系数:微分系数的调节是偏差变化量对于系统输出的影响程度。微分系数越大,系统对于偏差量的变化越敏感,越能提前响应,进而抑制超调,但是过大的微分系数则会让整个系统出现振荡。
试凑法
内容:
结合系统的具体情况以及经验,先试凑几组合理的 PID 系数,同时需要观察系统的曲线变化,确定每一个系数对于整个系统曲线的大致影响,然后再根据具体的曲线进行调整。
调节思路
① 先是比例(P),再积分(I),最后是微分(D)
② 按纯比例系统整定比例系数,使其得到比较理想的调节过程曲线,然后再把比例系数缩小 1.2 倍左右,将积分系数从小到大改变,使其得到较好的调节过程曲线
③ 在这个积分系数下重新改变比例系数,再看调节过程曲线有无改善
④ 如果有改善,可将原整定的比例系数减少,改变积分系数,这样多次的反复,就可得到合适的比例系数和积分系数
⑤ 如果存在外界的干扰,系统的稳定性不好,可把比例、积分系数适当减小,使系统足够稳定
⑥ 如果系统存在小幅度超调,可以将整定好的比例系数和积分系数适当减小,增大微分系数,以得到超调量最小、调节作用时间最短的系统曲线
临界比例法
内容
在闭环的控制系统里,将调节器置于纯比例作用下,从小到大逐渐调节比例系数,直到系统曲线出现等幅振荡,再根据经验公式计算参数。
调节思路
① 将积分、微分系数置零,比例度取适当值,平衡操作一段时间,使控制系统按纯比例作用的方式投入运行
② 慢慢地增大比例系数,细心观察曲线的变化情况。如果控制过程的曲线波动是衰减的,则把比例系数继续增大;如果曲线波动是发散的,则应把比例系数减小,直至曲线波动呈等幅振荡,此时记下临界比例系数 δK 和临界振荡周期 Tk 的值
③ 根据记下的比例系数和周期,采用经验公式,计算调节器的参数

一般调节法
内容
这种方法针对一般的 PID 控制系统所以称之为一般调节法。
调节思路
① 首先将积分、微分系数置零,使系统为纯比例控制。控制对象的值设定为系统允许的最大值的 60%~70%,接着逐渐增大比例系数,直至系统出现振荡;
此时再逐渐减小比例系数,直至系统振荡消失,然后记录此时的比例系数,并设定系统的比例系数为当前值的 60%~70%
② 确定比例系数后,设定一个较小的积分系数,然后逐渐增大积分系数,直至系统出现振荡;此时在逐渐减小积分系数,直至系统振荡消失,然后记录此时的积分系数,并设定系统的积分系数为当前值的 55%~65%
③ 微分系数一般不用设定,为 0 即可。若系统出现小幅度振荡,并且通过 PI 环节无法优化,这可以采用与确定比例、积分系数相同的方法,微分系数取系统不振荡时的 30%左右。
④ 系统空载、带载联调,再对 PID 参数进行微调,直至满足要求
在使用PID时,如果只使用一个参数是没有意义,至少使用两个参数,并且P(比例项)是必须要有的
虽然PID有三个参数,但大多数情况下PID三个参数并不是都使用上的,一般会其中两个来组合使用,比如PI组合用于追求稳定的系统,PD组合用于追求快速响应的系统
当然PID用于即追求稳定又追求快速响应的系统,但是实际上PID参数越多越难调,而且许多情况下两个参数的效果已经足够了,所以我一般根据情况使用前两个。
实际调参
从实际的 PID 系统曲线来理解 PID 各个系数的调节效果。
① 先调整比例系数,积分、微分系数设置为 0,此时的系统只有比例环节参与控制,此时系统的曲线出现大幅振荡。
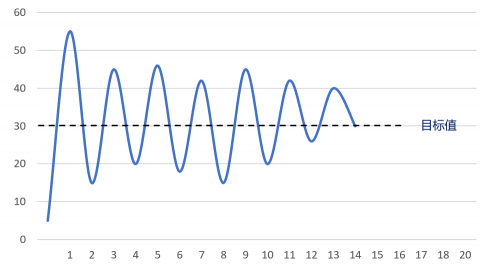
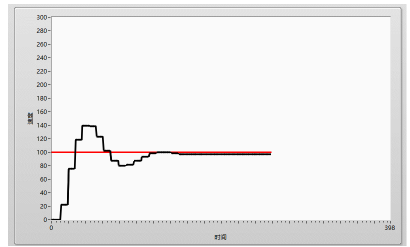
首先确定硬件上是否出现了故障,例如电压不稳定、电机堵转等,排除了这些之后,那就说明比例系数调节的过大了,这个时候我们可以把比例系数慢慢地减小,并同时观察曲线的变化。
② 当我们调小比例系数之后,曲线的大幅度振荡现象消失,但是曲线依旧存在小幅度的超调现象,并且此时通过调节比例系数已经无法优化曲线。
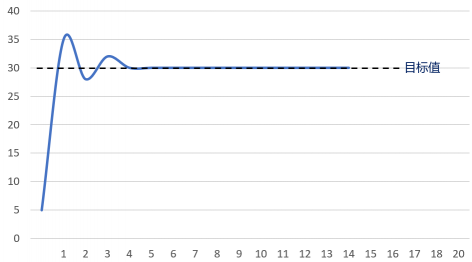
此时,我们可以慢慢地增大微分系数,并同时观察曲线的变化,从而找到最合适的参数。
增大微分系数之后,如果系统的曲线已经较为理想,则说明这个系统只需要比例和微分环节的控制。
③ 如果在纯比例环节的控制下,系统的实际值始终达不到目标值,存在静态误差。
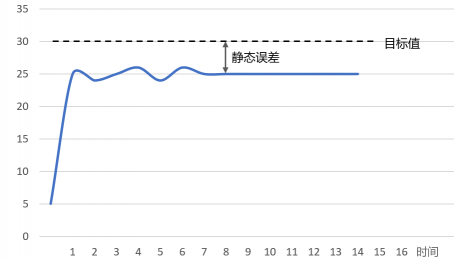
此时,可以逐渐增大积分系数,并同时观察曲线的变化,如果消除静差的时间过长,则可以再适当增大积分系数,但是需要注意兼顾系统的超调量。
经过调整之后,如果系统的曲线已经较为理想,则说明这个系统只需要比例和积分环节的控制。
④ 如果系统在比例和积分环节的控制下出现小幅度的超调现象,可以慢慢地增大微分系数,并同时观察曲线的变化,从而找到最合适的参数。
以上就是在实际调参中经常遇到的一些问题以及解决方法。在实际应用中,控制系统是多样且复杂的,这一些方法只能作为参考,并不是通用的,因此在 PID 调参过程中,要注意经验的积累。
参考Code
PID初始化代码
定义一个新的PID参数时,就是建立一个新的结构体,运算和初始化时直接调用对应的成员变量就行,十分方便简洁,具体定义的结构体如下:
typedef struct{//PID运算模式uint8_t mode;//PID 三个基本参数__IO float Kp;__IO float Ki;__IO float Kd;__IO float max_out; //PID最大输出__IO float max_iout; //PID最大积分输出__IO float2 set; //PID目标值__IO float2 fdb; //PID当前值__IO float out; //三项叠加输出__IO float Pout; //比例项输出__IO float Iout; //积分项输出__IO float Dout; //微分项输出//微分项最近三个值 0最新 1上一次 2上上次__IO float Dbuf[3];//误差项最近三个值 0最新 1上一次 2上上次__IO float error[3];} pid_type_def;
初始运行时调用一次,初始化各个参数
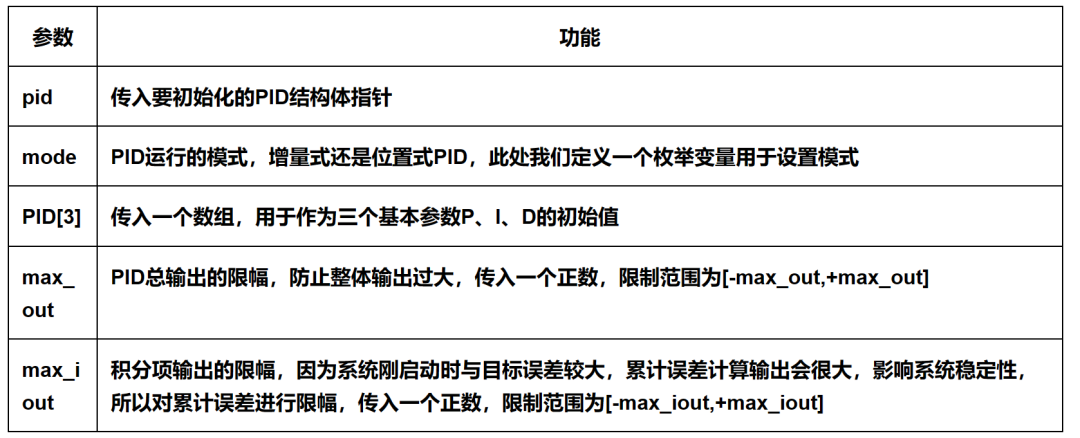
void Own_PID_init(pid_type_def *pid, uint8_t mode, const __IO float PID[3], __IO float max_out, __IO float max_iout){if (pid == NULL || PID == NULL){return;}pid->mode = mode;pid->Kp = PID[0];pid->Ki = PID[1];pid->Kd = PID[2];pid->max_out = max_out;pid->max_iout = max_iout;pid->Dbuf[0] = pid->Dbuf[1] = pid->Dbuf[2] = 0.0f;pid->error[0] = pid->error[1] = pid->error[2] = pid->Pout = pid->Iout = pid->Dout = pid->out = 0.0f;}
PID运算代码
__IO float PID_calc(pid_type_def *pid, __IO float ref, __IO float set){//判断传入的PID指针不为空if (pid == NULL){return 0.0f;}//存放过去两次计算的误差值pid->error[2] = pid->error[1];pid->error[1] = pid->error[0];//设定目标值和当前值到结构体成员pid->set = set;pid->fdb = ref;//计算最新的误差值pid->error[0] = set - ref;//判断PID设置的模式if (pid->mode == PID_POSITION){//位置式PID//比例项计算输出pid->Pout = pid->Kp * pid->error[0];//积分项计算输出pid->Iout += pid->Ki * pid->error[0];//存放过去两次计算的微分误差值pid->Dbuf[2] = pid->Dbuf[1];pid->Dbuf[1] = pid->Dbuf[0];//当前误差的微分用本次误差减去上一次误差来计算pid->Dbuf[0] = (pid->error[0] - pid->error[1]);//微分项输出pid->Dout = pid->Kd * pid->Dbuf[0];//对积分项进行限幅LimitMax(pid->Iout, pid->max_iout);//叠加三个输出到总输出pid->out = pid->Pout + pid->Iout + pid->Dout;//对总输出进行限幅LimitMax(pid->out, pid->max_out);}else if (pid->mode == PID_DELTA){//增量式PID//以本次误差与上次误差的差值作为比例项的输入带入计算pid->Pout = pid->Kp * (pid->error[0] - pid->error[1]);//以本次误差作为积分项带入计算pid->Iout = pid->Ki * pid->error[0];//迭代微分项的数组pid->Dbuf[2] = pid->Dbuf[1];pid->Dbuf[1] = pid->Dbuf[0];//以本次误差与上次误差的差值减去上次误差与上上次误差的差值作为微分项的输入带入计算pid->Dbuf[0] = (pid->error[0] - 2.0f * pid->error[1] + pid->error[2]);pid->Dout = pid->Kd * pid->Dbuf[0];//叠加三个项的输出作为总输出pid->out += pid->Pout + pid->Iout + pid->Dout;//对总输出做一个先限幅LimitMax(pid->out, pid->max_out);}return pid->out;}
{ \(input > max) \{ \input = max; \} \(input < -max) \{ \input = -max; \} \}
PID数据清空代码
有时候需要清除中间变量,例如目标值和中间变量清零。
void PID_clear(pid_type_def *pid){if (pid == NULL){return;}//当前误差清零pid->error[0] = pid->error[1] = pid->error[2] = 0.0f;//微分项清零pid->Dbuf[0] = pid->Dbuf[1] = pid->Dbuf[2] = 0.0f;//输出清零pid->out = pid->Pout = pid->Iout = pid->Dout = 0.0f;//目标值和当前值清零pid->fdb = pid->set = 0.0f;}
处理PID算法还有很多算法,例如lqr算法等,项目这个开源项目就是lqr实现的。后面会详细介绍制作过程和算法。



👇👇点这里抢先兑换好礼!