（1） ◎ 解答:
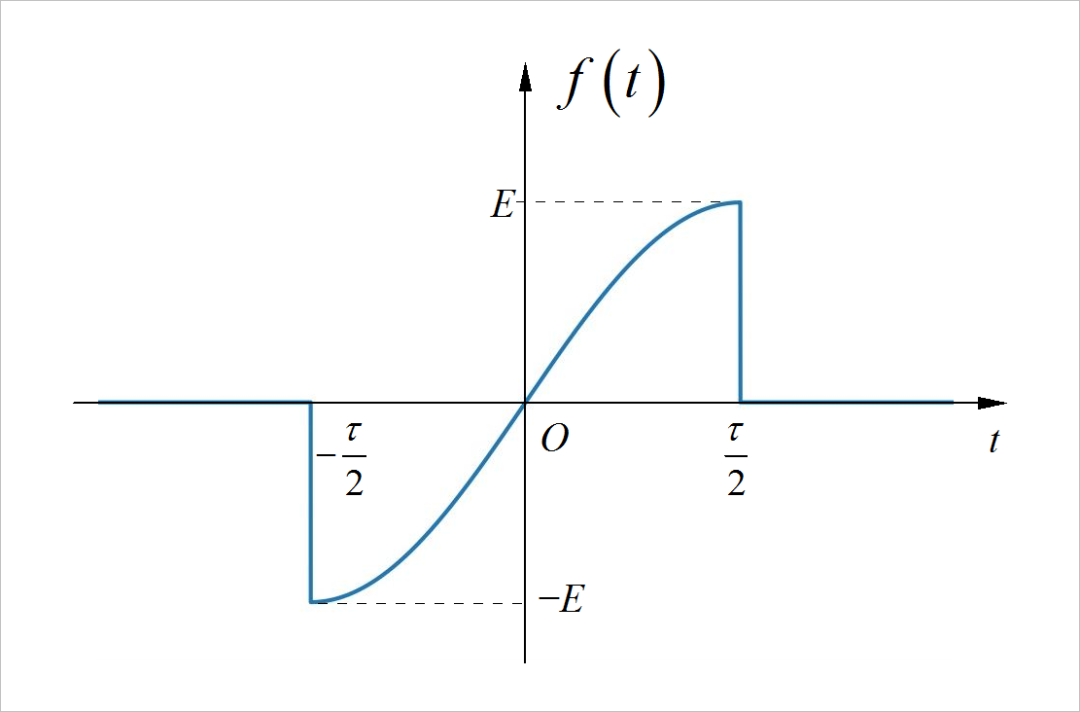
▲ 图1.1.1 奇对称半波正弦脉冲信号根据波形可以知道信号的表达式为：
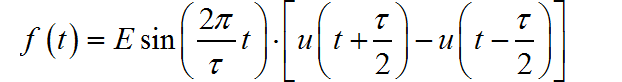
根据傅里叶变换公式，该信号的频谱为：
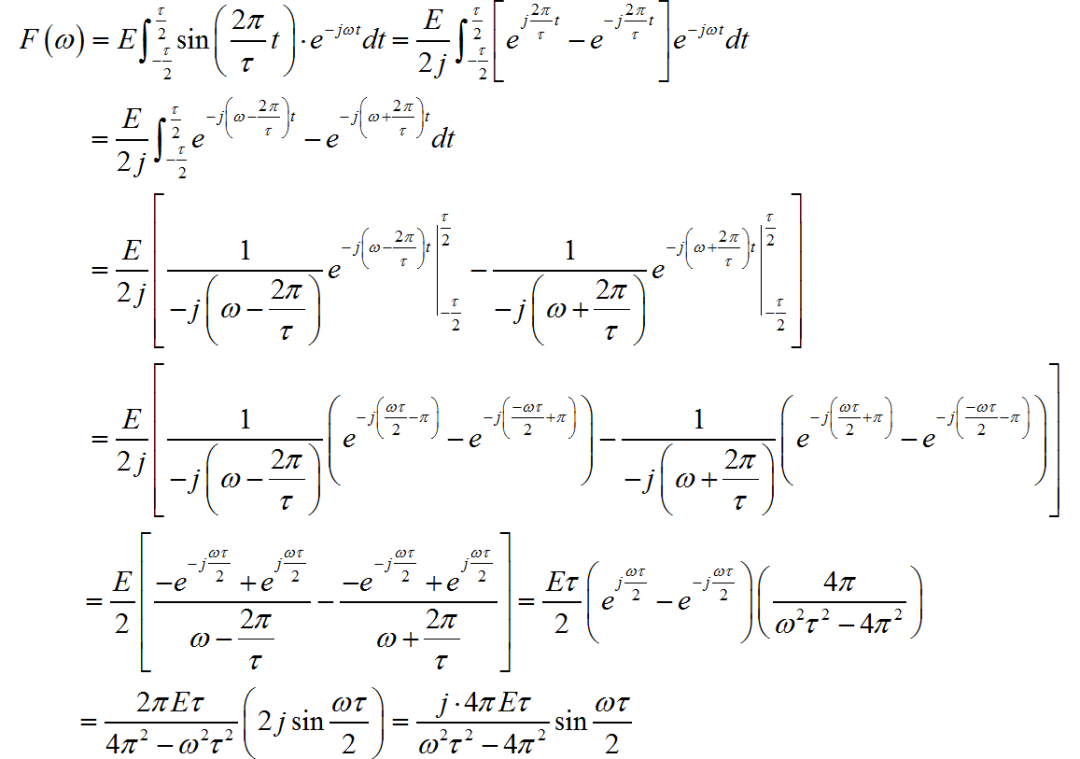
下面利用 Sympl 中的符号推导验证 一下上面答案的正确性。
x,T,t,n = symbols('x,T,t,n')
o,E,a = symbols('omega,E,tau')
Fo = E*integrate(sin(2*pi*t/a)*exp(-I*o*t),(t,-a/2,a/2))
result = simplify(Fo)
下面是 Sympl 积分后给出的答案， 可以看到它 与前面的答案是一致的。
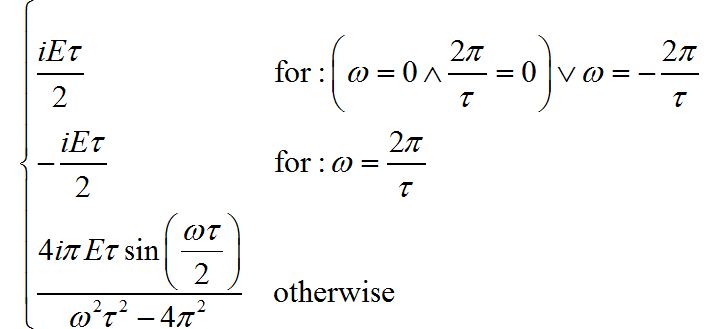
（2） ◎ 求解：
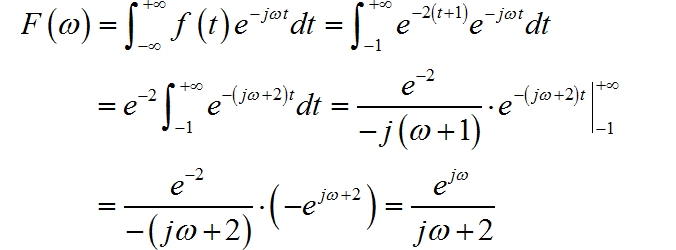
（3）◎ 解答：
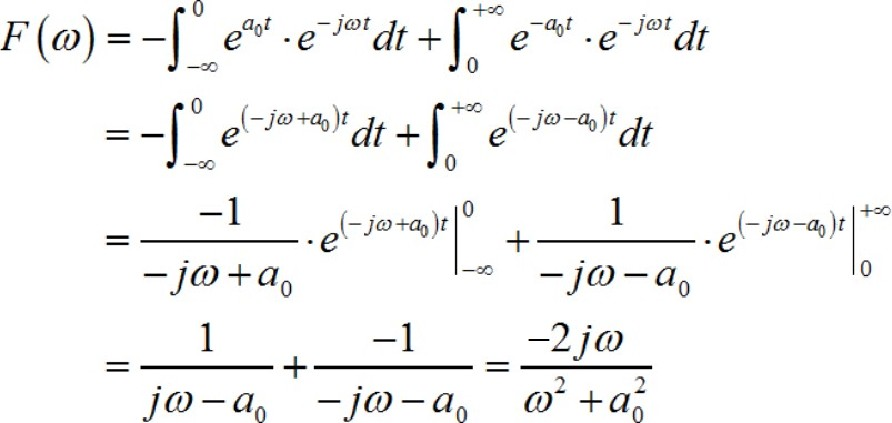
（4） ◎ 解答：
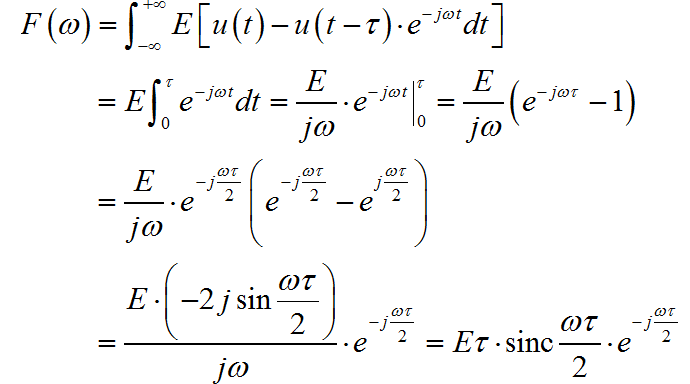
（1） ◎ 解答
▲ 图1.1.2 信号的波形通过给定的 f(t) 的波形，可以看到它可以通过 宽度为 ，高度为 E 的矩形信号 减去 同样宽度和高度的等腰三角形信号 获得。对于 的频谱分别是：
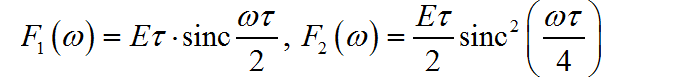
所以题目波形对应的信号的频谱为：
（2） ◎ 解答：
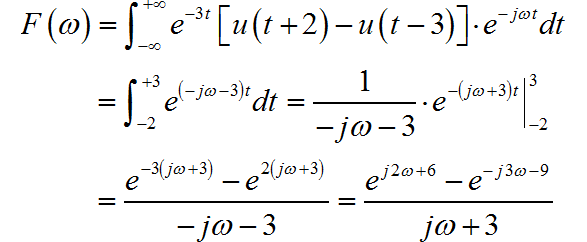
（1） ◎ 解答：
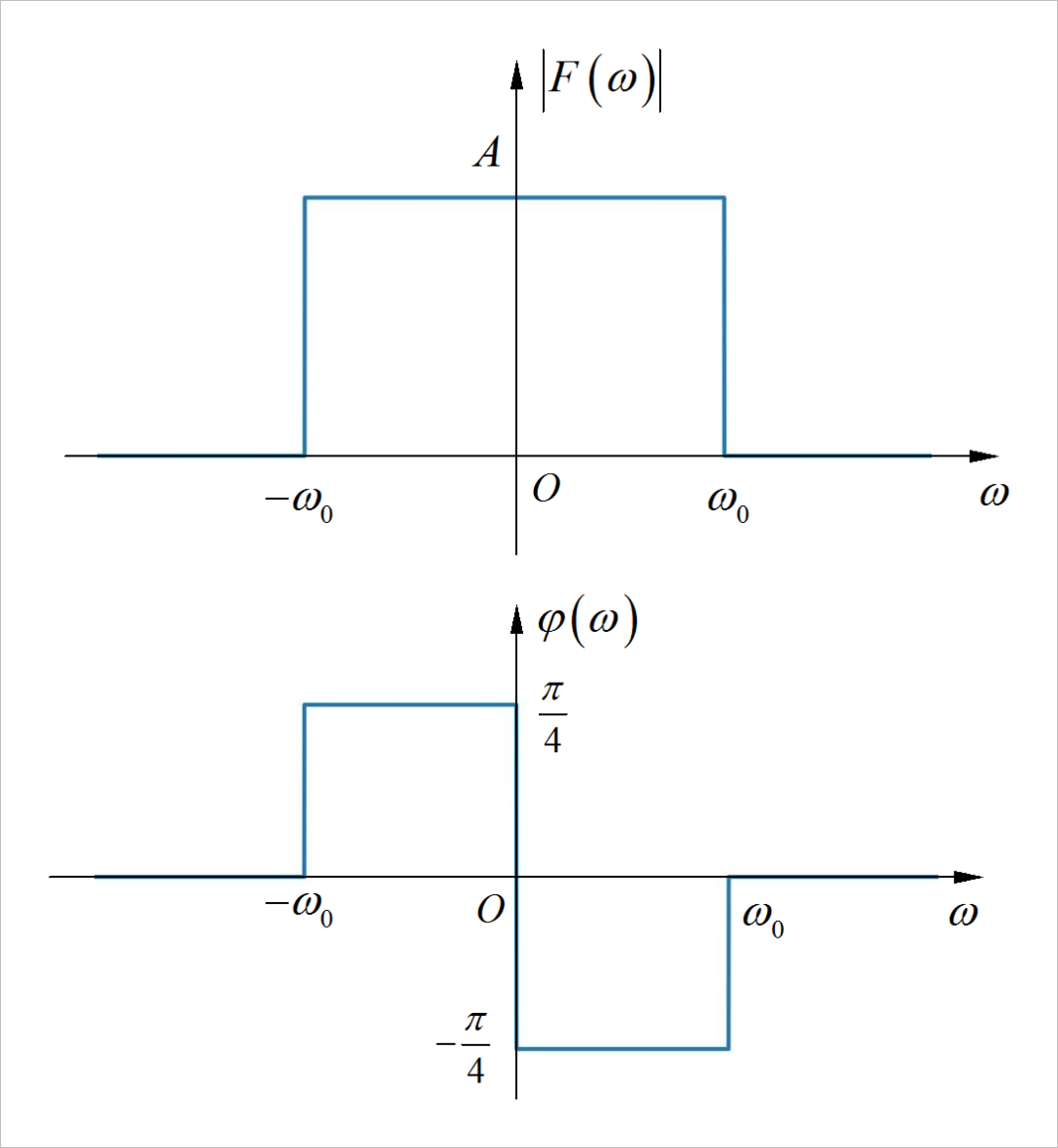
▲ 图1.2.1 信号的幅度谱和相位谱（2）◎ 解答：
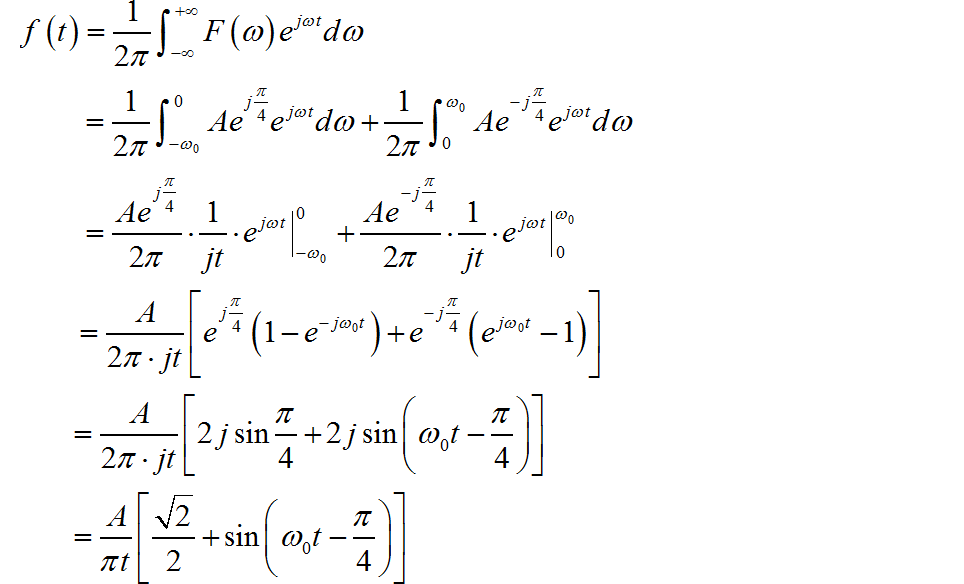
下面是信号的波形。其中参数 。
▲ 图1.2.2 信号的波形为了验证一下上述结果， 下面使用 Python 程序，利用 IFFT 工具，将给定的频谱进行反变换，对比一下结果与理论推导之间是否一致。
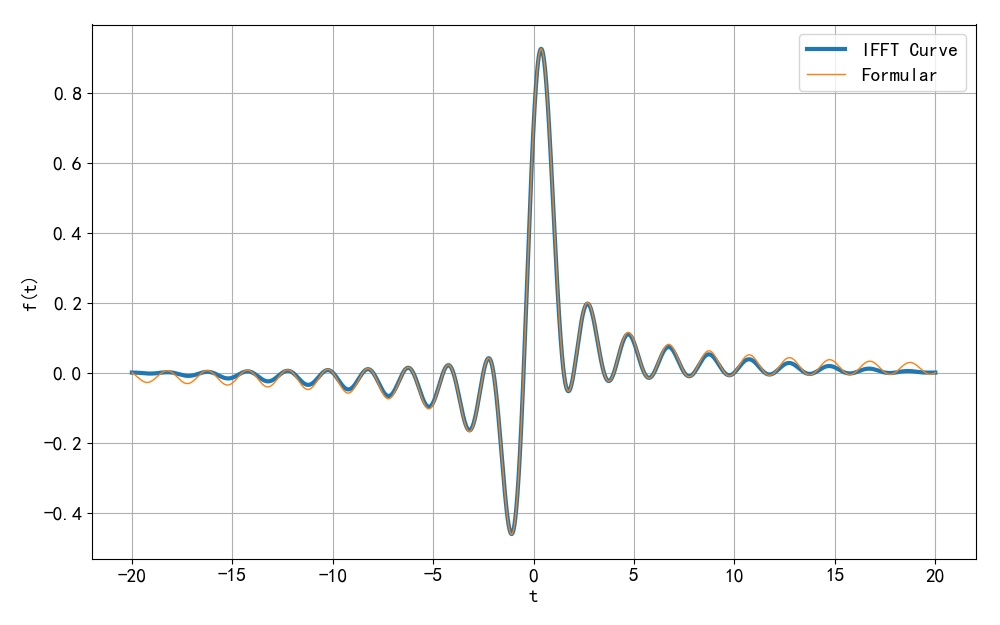
▲ 图1.2.3 利用 IFFT 将频谱进行反变换，获得对应的信号波形from headm import *
A=1
o0 = pi
tn = 100000
startt = -20
endt = -startt
ts = (endt-startt)/tn
os = 2*pi/ts
o1 = 2*pi/(endt-startt)
starto = -os/2
endo = os/2
onum = int(os/o1)
t = linspace(startt, endt, tn)
def G(t, startn, endn):
return heaviside(t-startn,0.5)-heaviside(t-endn,0.5)
def Gt(t, center, width):
startn = center-width/2
endn = startn + width
return heaviside(t-startn,0.5)-heaviside(t-endn,0.5)
o = linspace(starto, endo, len(t))
amp = G(o, -o0, o0)*A
phase = G(o, -o0, 0)*pi/4 + G(o, 0, o0)*(-pi/4)
cn = len(o)//2
Fo = amp*exp(1j*phase)
Fo = list(Fo)
Fo = Fo[cn:]+Fo[:cn]
ft = real(fft.ifft(Fo))/ts
ft = list(ft)
ft = ft[cn:]+ft[:cn]
plt.plot(t, ft, lw=3,label='IFFT Curve')
plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.grid(False)
plt.tight_layout()
ft = A/pi/t*(sqrt(2)/2+sin(o0*t-pi/4))
plt.plot(t, ft, lw=1, label='Formular')
printff(min(ft), max(ft))
plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
（2） ◎ 解答：
根据 的表达式，将其进行因式分解：
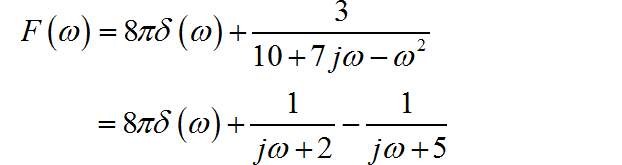
根据每一个因式， 可以写出各自对应的因果信号时域表达式，将它们叠加在一起，得到 对应的时域信号：
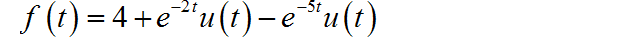
（1） ◎ 解答：
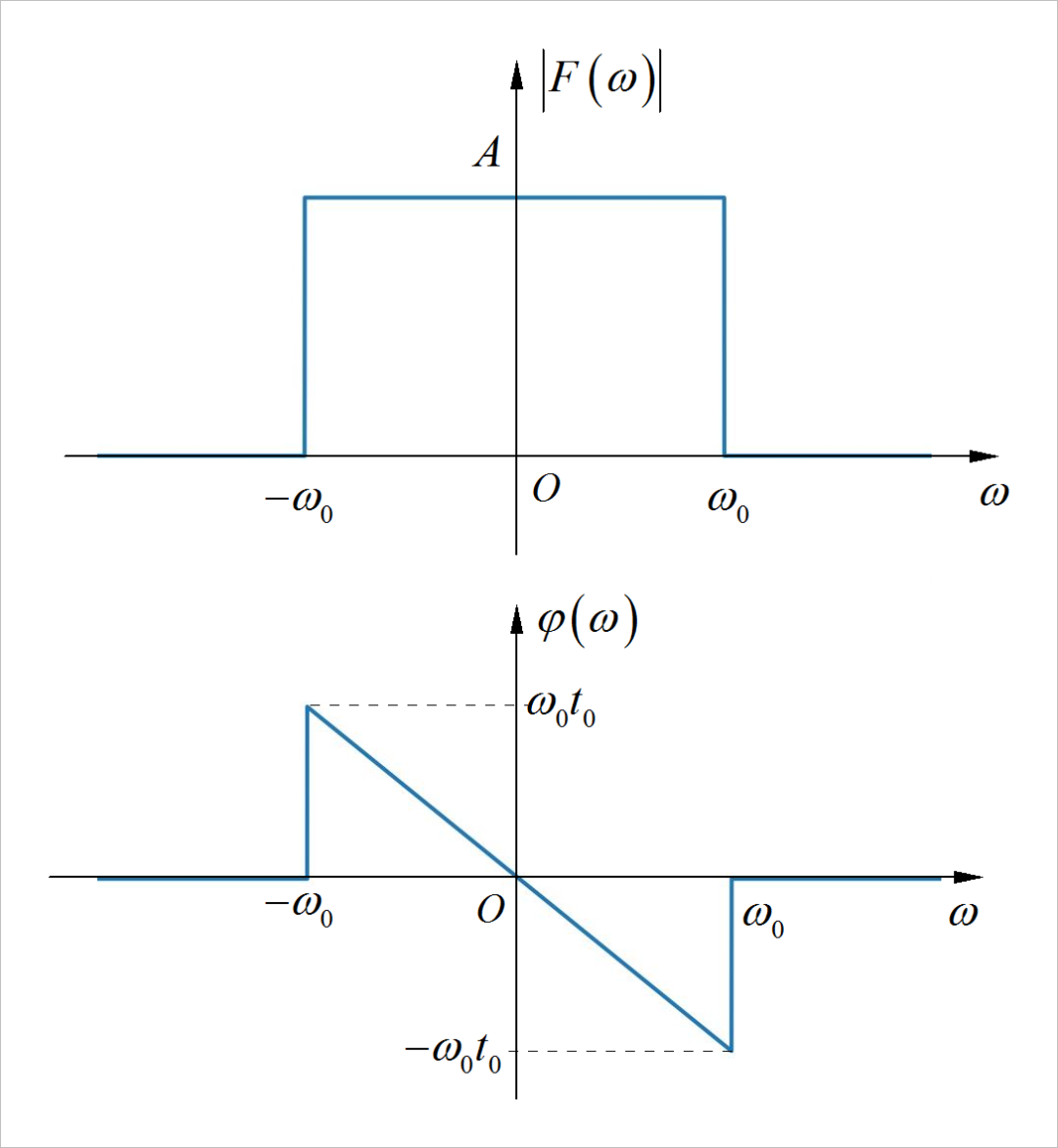
▲ 图1.2.4 信号的幅度谱和相位谱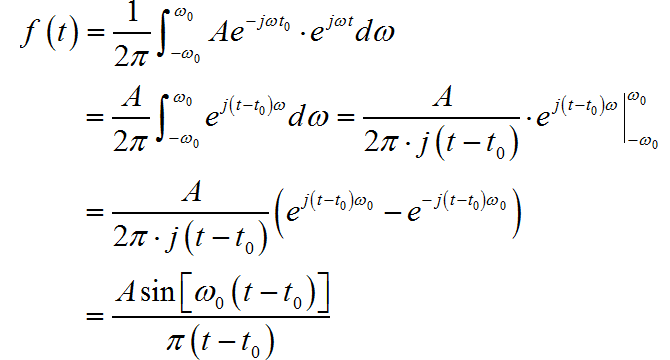
利用 IFFT 对频谱数值反变换， 并与上面解答曲线绘制在一起，其中参数 。可以看到它们之间几乎是重合的。
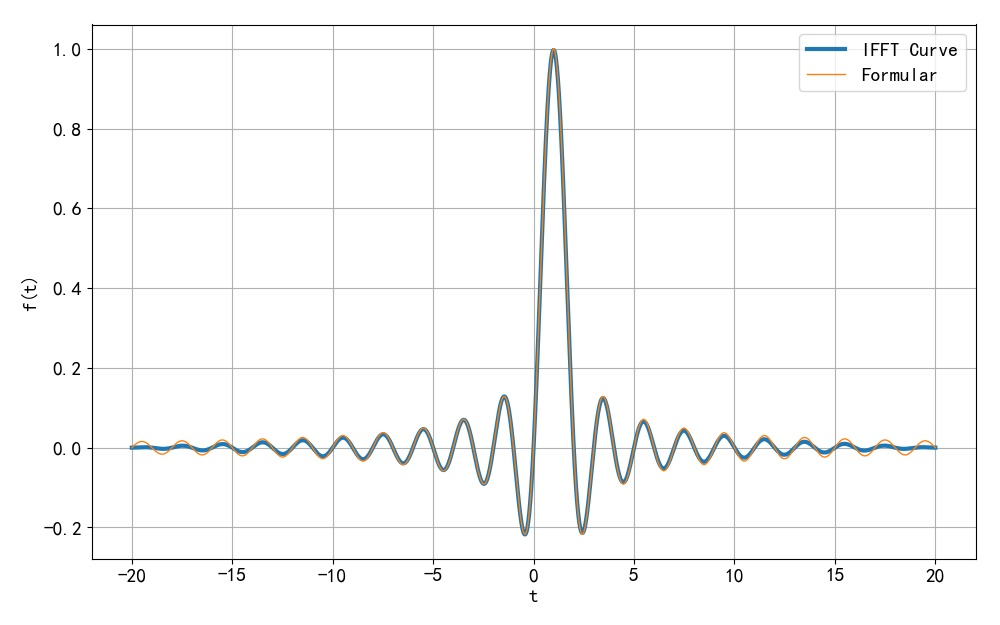
▲ 图1.2.5 利用IFFT 进行反变换与推导出的公式进行对比（2） ◎ 解答：
根据给定频谱图像，可以得到 的表达式：
已知
根据傅里叶变换的对偶性质：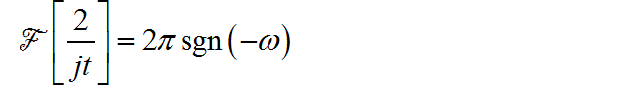
所以
由此可知
（1） ◎ 解答：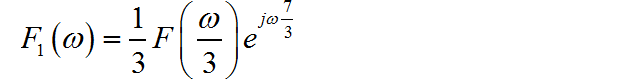
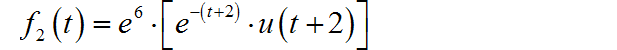
（2） ◎ 解答：
（3） ◎ 解答：
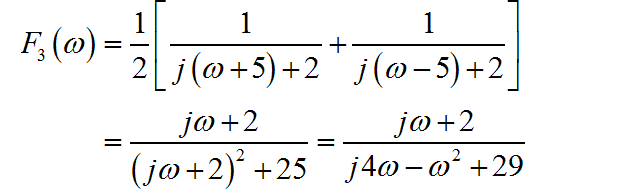（4） ◎ 求解：
（5） ◎ 求解：
对于中心在原点，宽度为 B， 高度为 A 的方波 频谱， 对应的时域信号为：
根据傅里叶变换频移特性， 原图频谱对应的时域信号为：
（1） ◎ 解答：
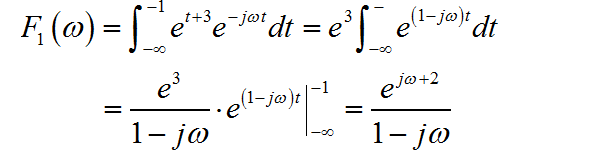
（2） ◎ 求解：
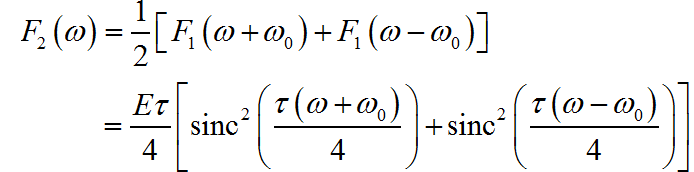
考虑时移之后的结果：
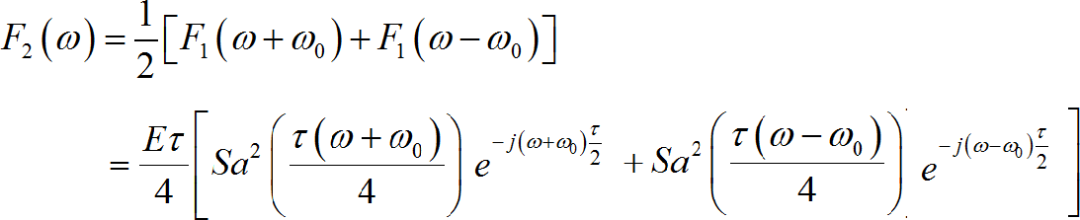
（1） ◎ 解答：
根据傅里叶变换时移特性：
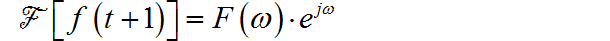所以：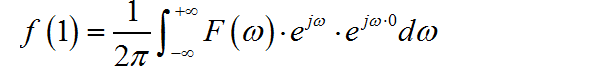
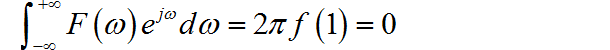
（2） ◎ 解答：
的傅里叶反变换对应着 的偶分量：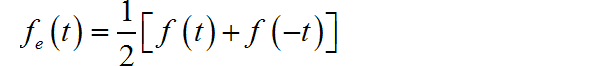
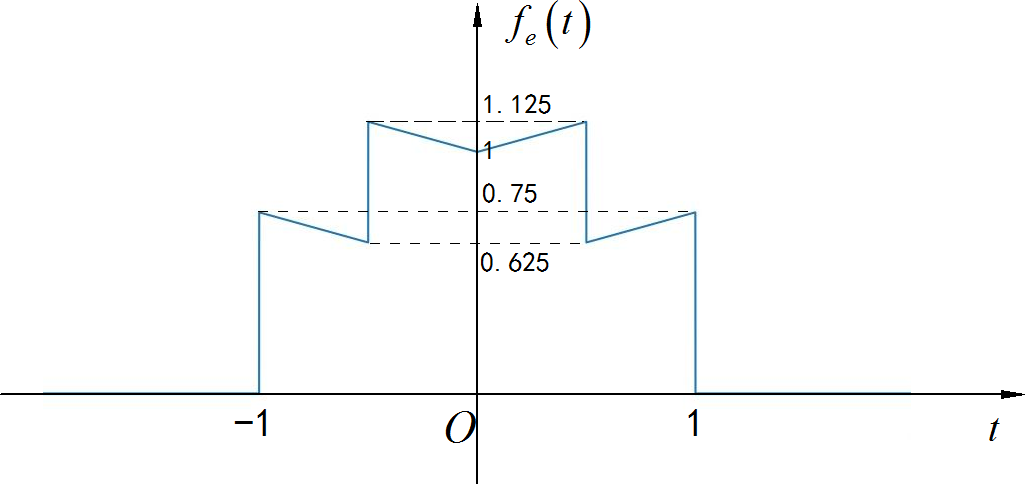
▲ 图1.4.1 信号的偶分量（3） ◎ 求解：
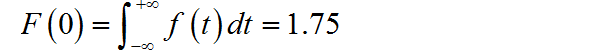
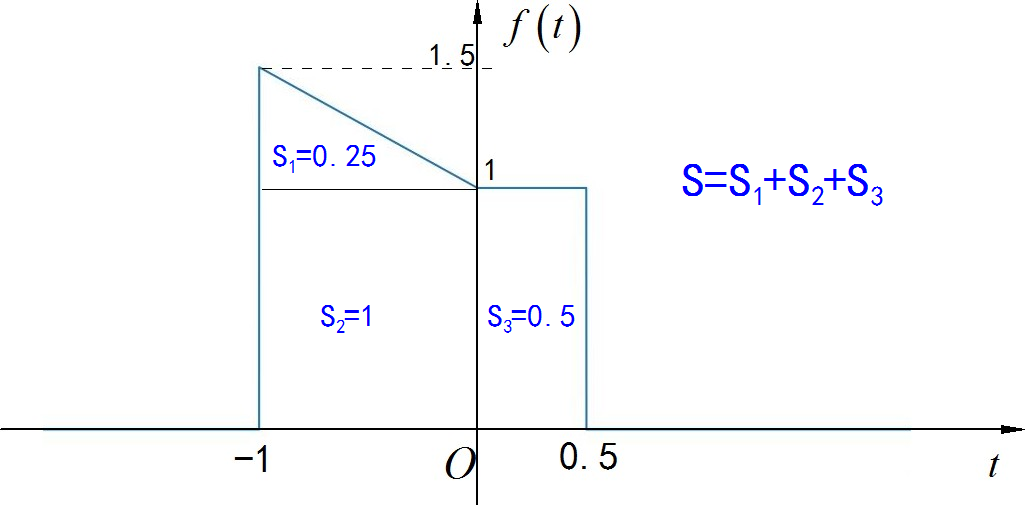
▲ 图1.4.2 信号的面积信号与系统 2023（春季） 作业要求 - 第六次作业: https://zhuoqing.blog.csdn.net/article/details/129854671
