
(1)第一小题
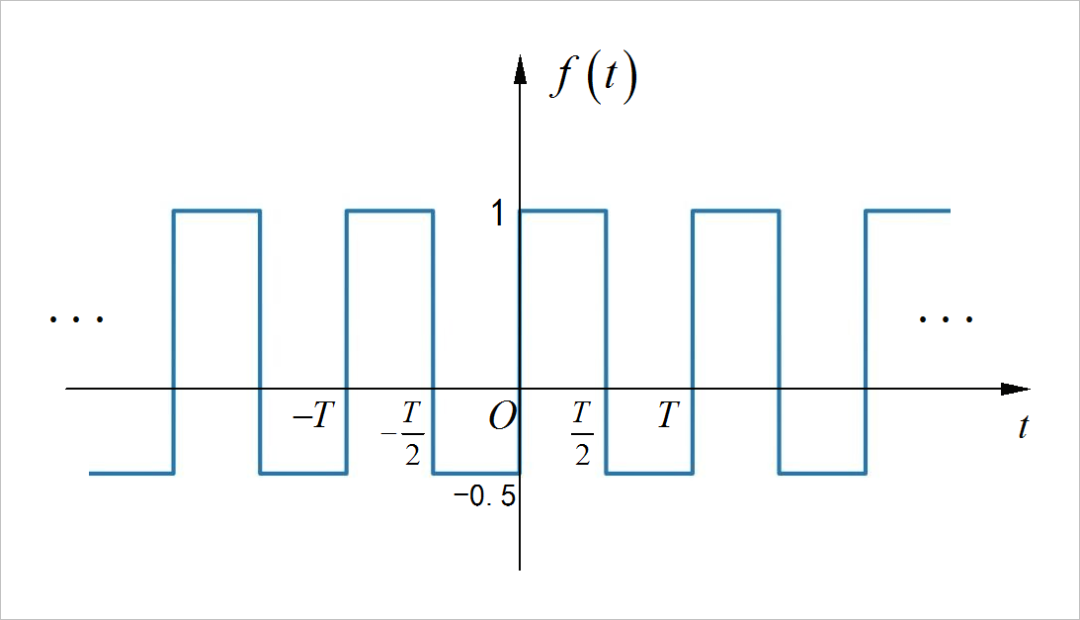
▲ 图1.1.1 周期信号第一小题◎ 求解:
在求解过程中, 令 ,根据傅里叶级数分解公式,
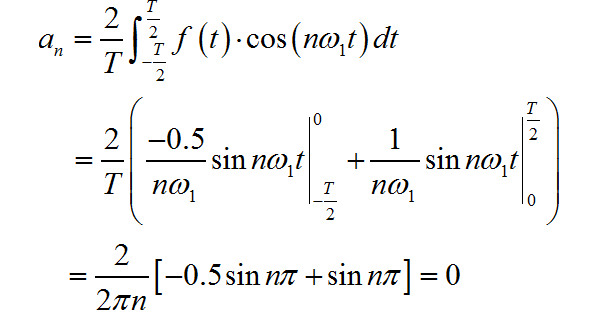
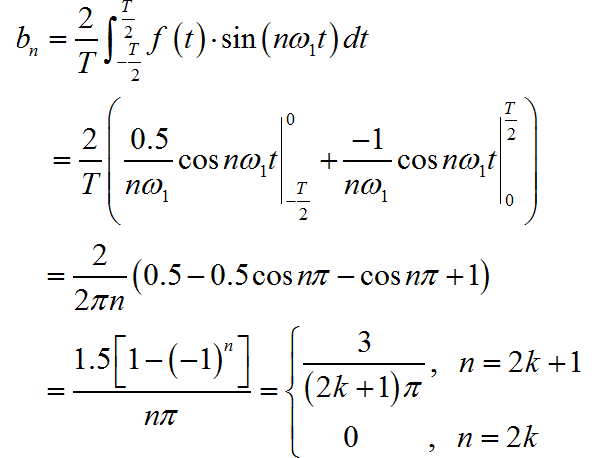
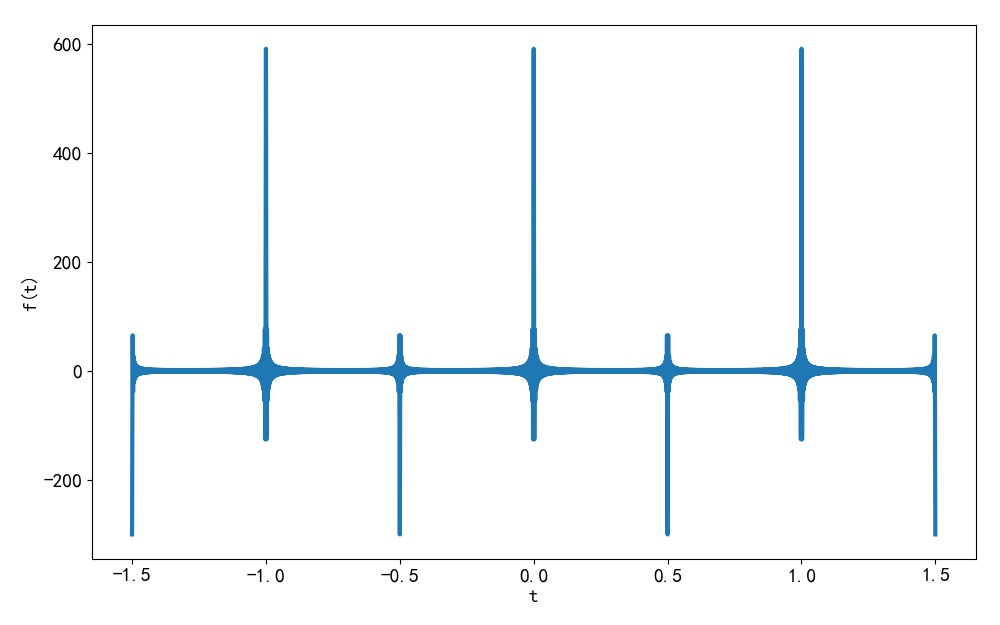
下面通过 Python 编程, 利用上面推导出来的傅里叶级数分解系数公式,取前 N=300项谐波进行叠加,绘制出相应的综合波形。其中周期 T=2。验证上述公式正确性。
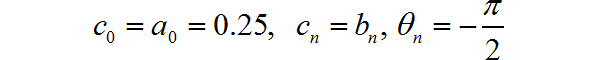
在合成的波形中, 在信号间断点处能够观察到明显的吉布斯过冲振荡现象。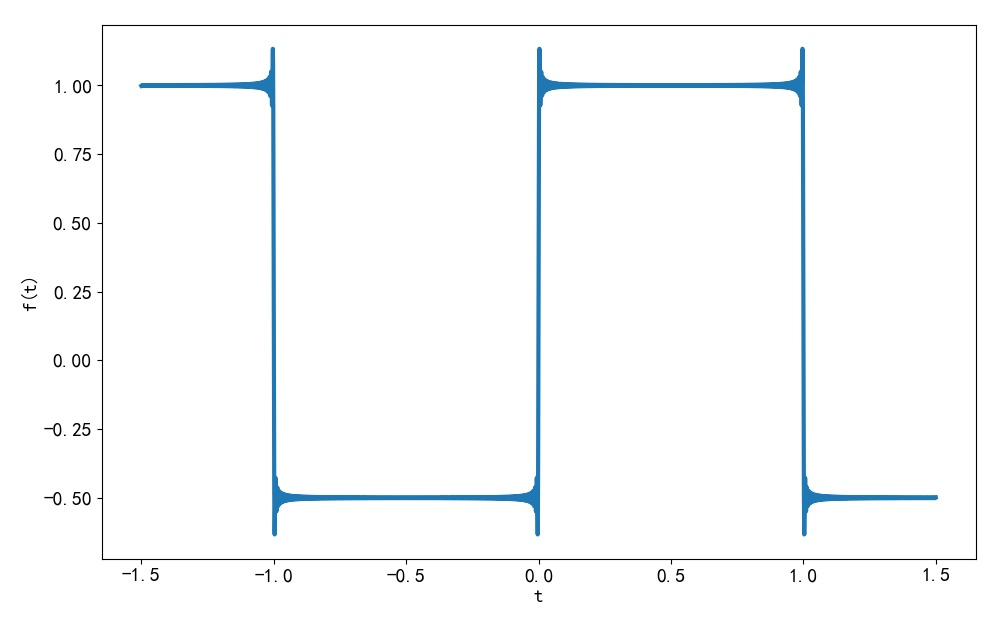
▲ 图1.1.2 使用前 300项谐波合成的信号波形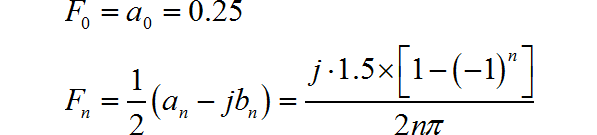
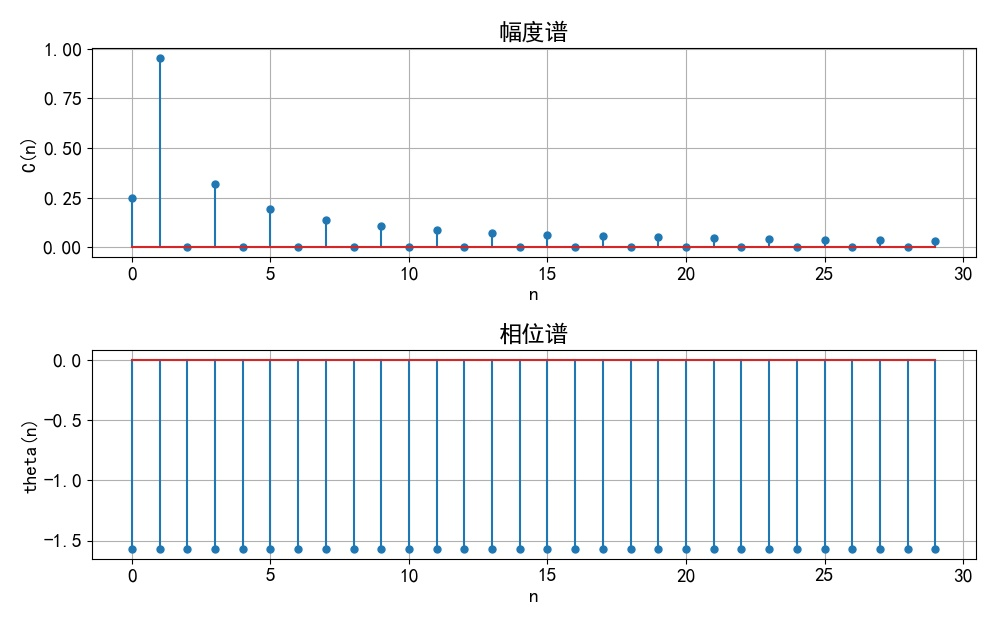
▲ 图1.1.3 周期信号的单边频谱(2)第二小题

▲ 图1.1.4 周期信号第二小题◎ 求解:
在求解过程中, 令 ,根据傅里叶级数分解公式,
信号是奇对称信号,所以: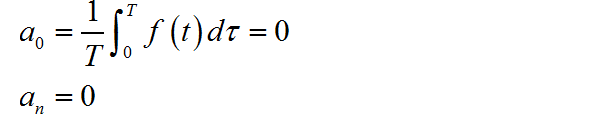
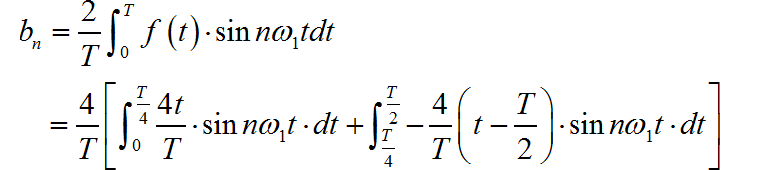
上面这个积分看起来挺吓人的,对于是否能够 一次性推导出来没有太大的信心。下面借助于 Sympy 符号公式推导软件帮助完成计算。
下面是软件给出的结果。由于此时 ,所以下面公式还可以进一步化简。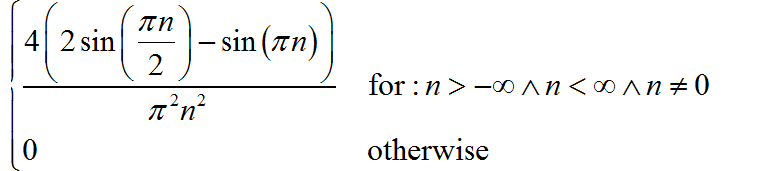
化简得到 的表达式为:

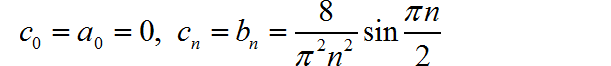
下面是利用上面给出的傅里叶级数分解共识,将前面 300 项进行叠加所获得波形, 其中令 T = 1。可以看到这个波形与给定的作业波形是一致的。从另外一个方面也验证了所得到的公式的正确性。

▲ 图1.1.5 使用前300项傅里叶级数合成的信号波形
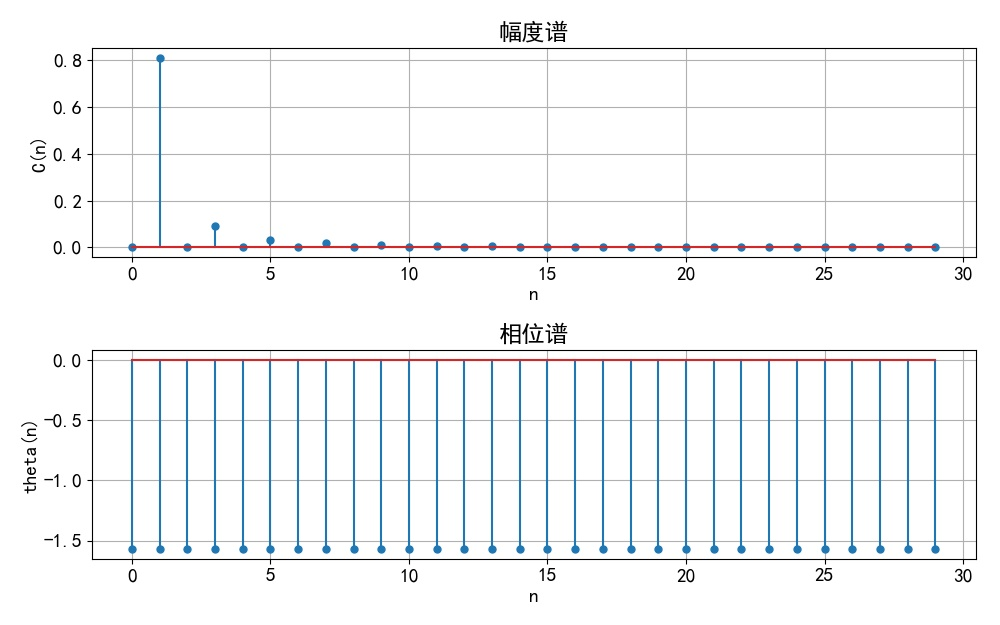
▲ 信号的单边频谱(3)第三小题
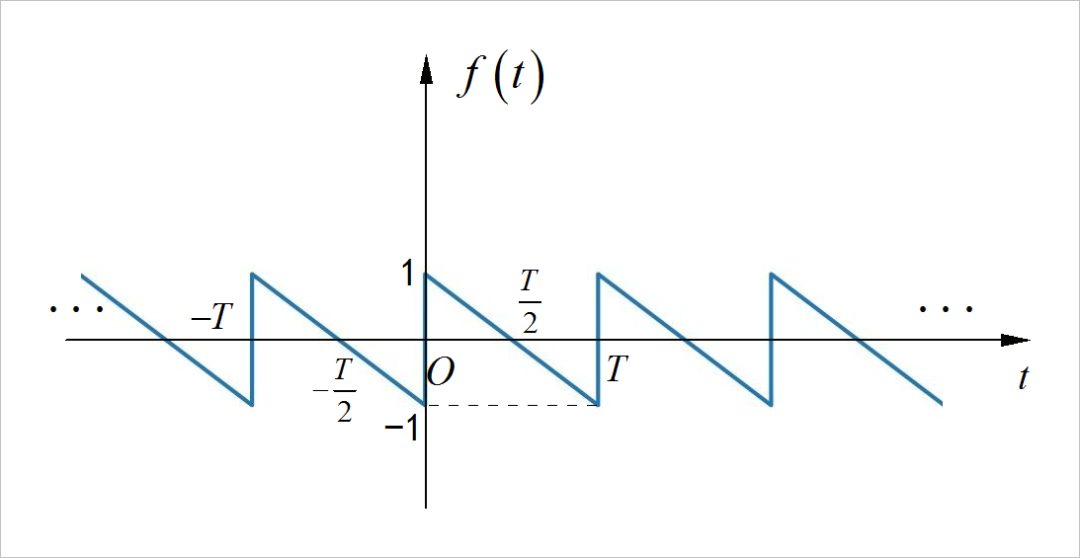
▲ 图1.1.4 周期信号第三小题◎ 求解:
在求解过程中, 令 ,根据傅里叶级数分解公式,
信号是一个奇对称信号, 所以有:
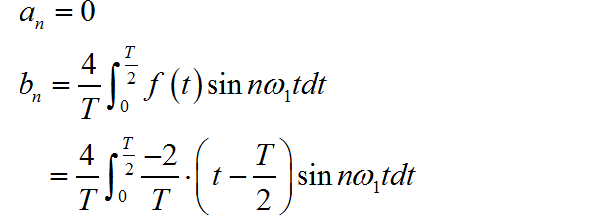
下面仍然使用 sympl 符合推导,获得上面 bn 的积分表达式。

根据上面结果,可以获得 bn 的表达式:


下面是傅里叶级数前 300 项叠加后的波形,其中信号周期 T=1。可以看到它与题目给定的波形是一致的,能够在信号间断点出观察到明显的吉布斯 过冲振荡。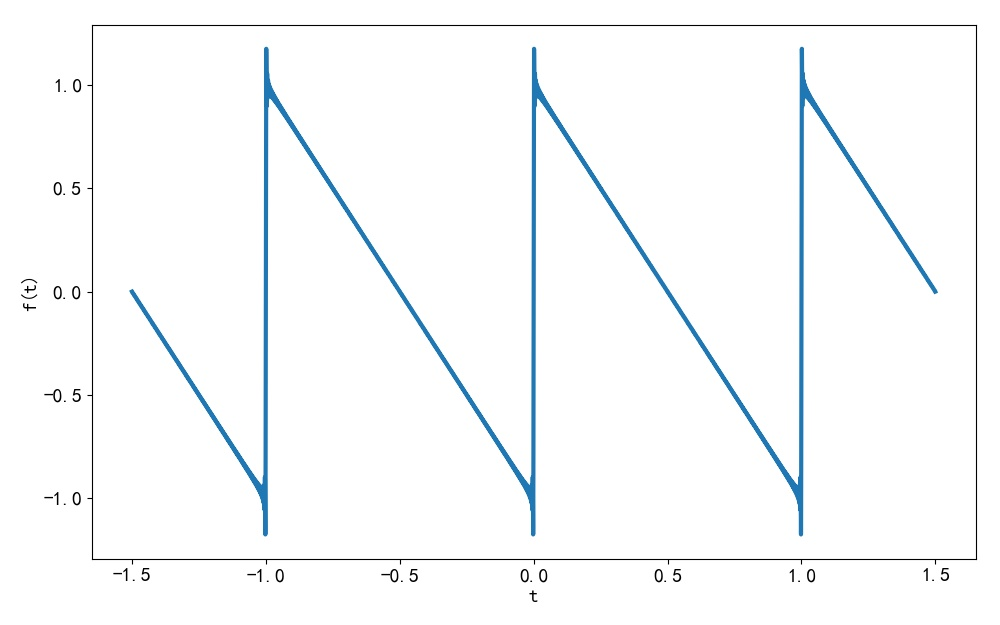
▲ 图1.1.8 信号傅里叶级数前 300 项叠加的波形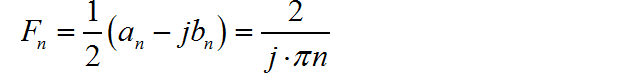
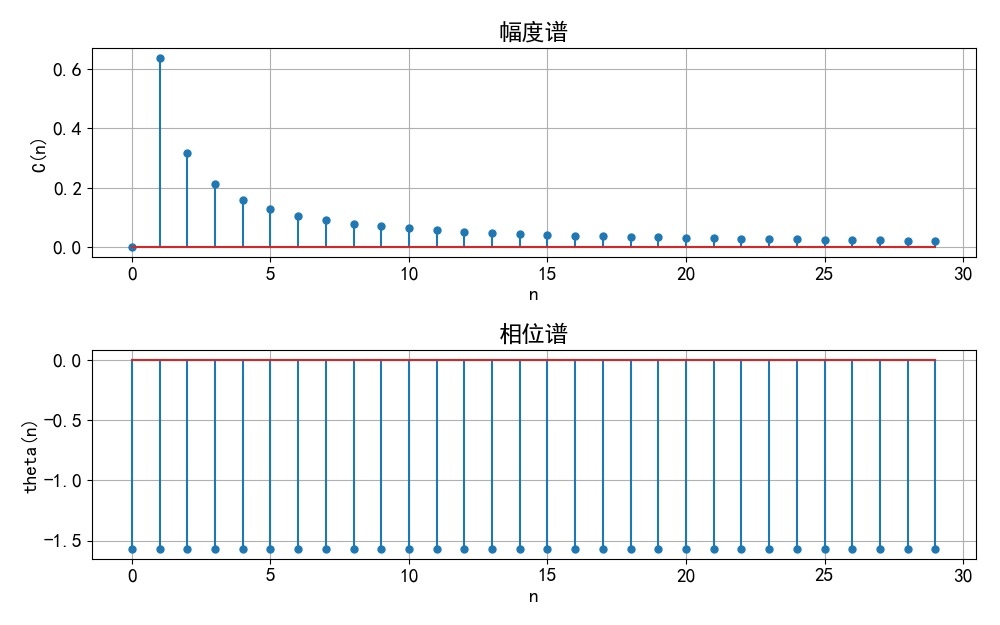
▲ 图1.1.9 信号的单边频谱 (4)选做题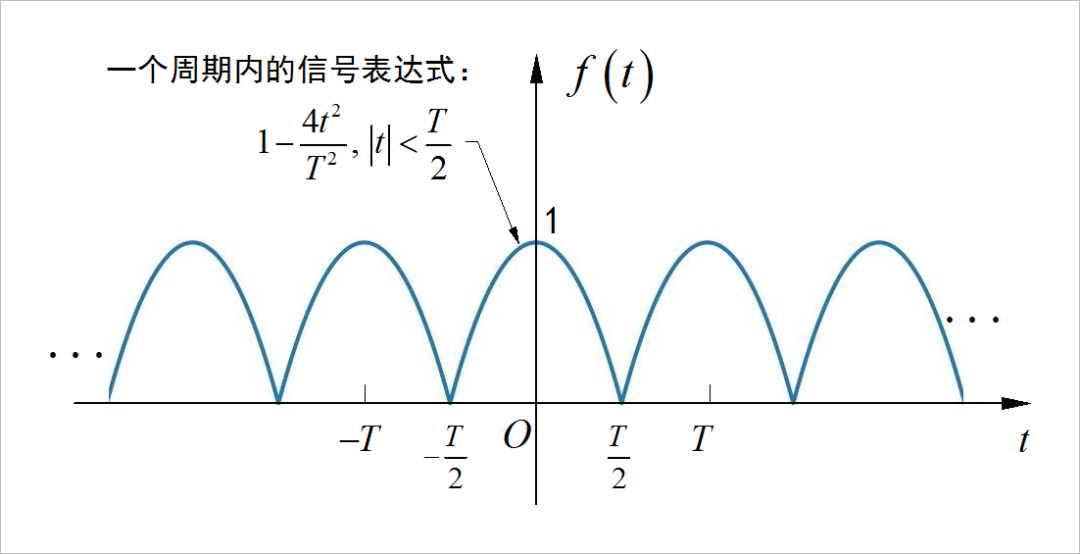
▲ 图1.1.6 周期信号选做题◎ 求解:
这是一个偶对称的周期信号,所以其中的 bn 分量为 0。


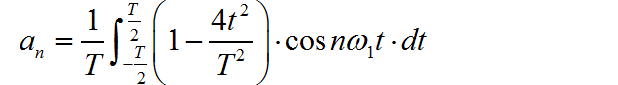
下面是 sympl 给出的 an 积分公式:
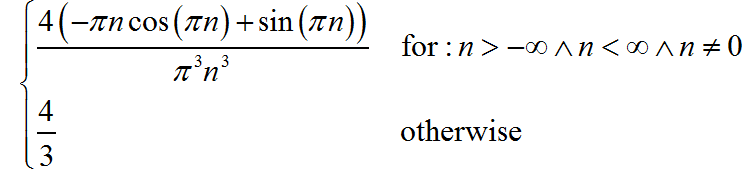
整理一下,可以得到:

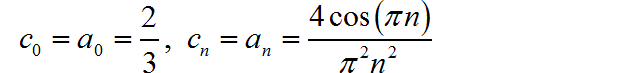
下面利用上述傅里叶分解公式,使用前级数300项绘制出对应的波形。其中周期 T= 1。可以看到与给定的波形是相同的。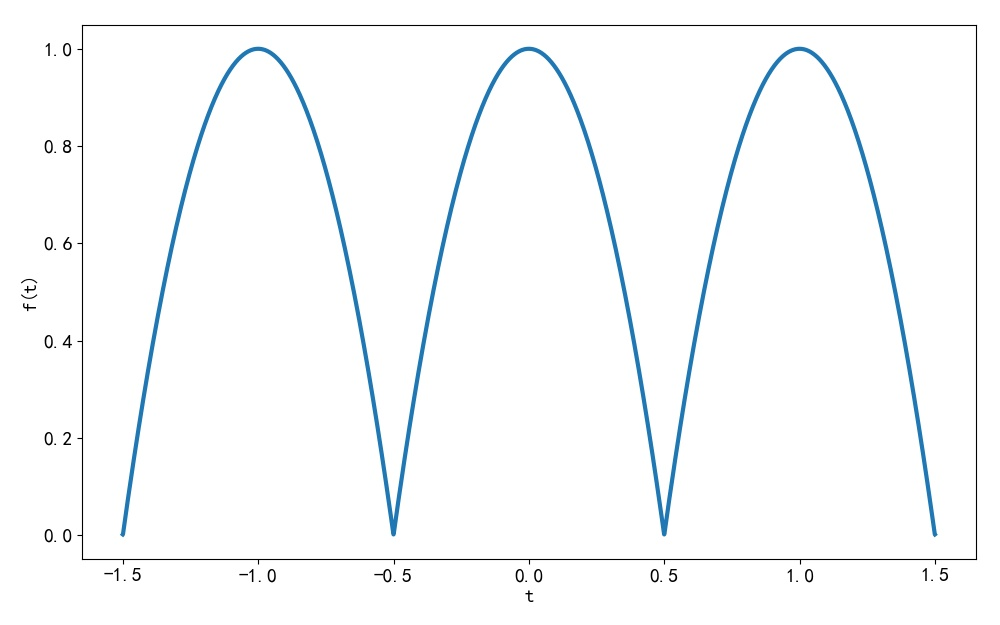
▲ 图1.1.11 使用傅里叶级数前300项合成的信号波形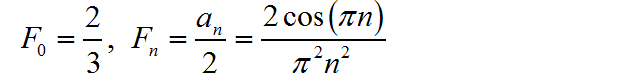

▲ 图1.1.12 信号的单边频谱(5)第五小题
▲ 图1.1.13 周期信号第五小题◎ 求解:
这是一个偶对称的周期信号,所以其中的 bn 分量为 0。


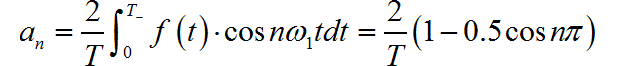
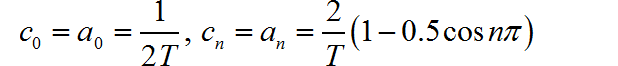
▲ 使用傅里叶级数前300项合成的信号波形复指数形式傅里叶级数分解系数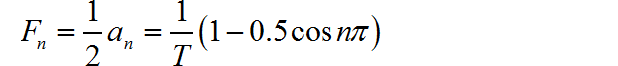
信号的单边频谱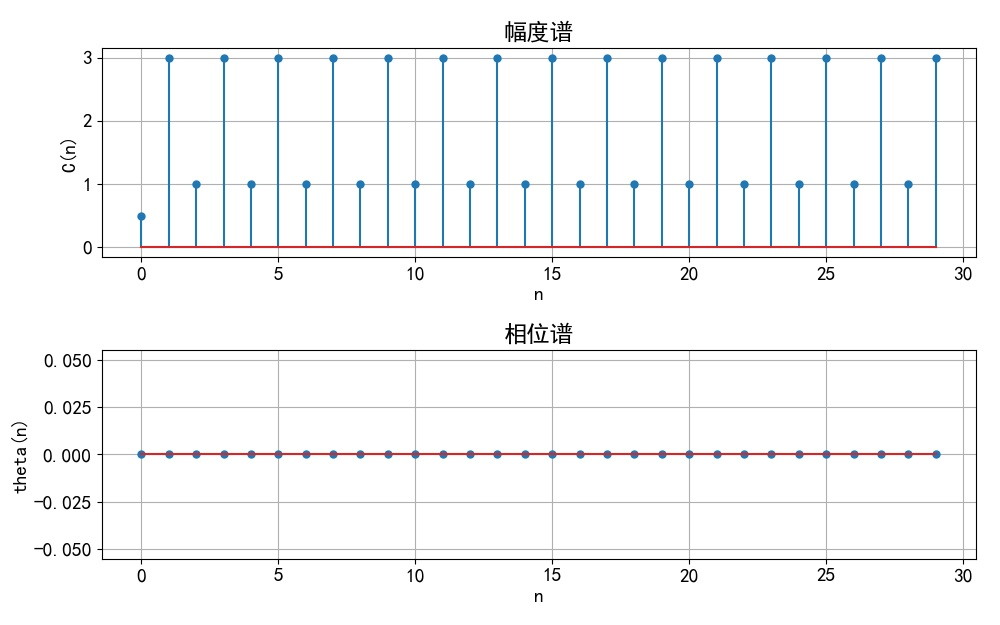
▲ 信号的单边频谱◎ 求解:
(1) 根据信号表达式可以知道其中包括有 直流分量,三个谐波角频率分别为 2、3、5。所以信号的基频对应的角频率为 1 。
(2) 为了绘制 f(t) 的幅度谱和相位谱, 根据三角恒等式,将信号表达式转换成 的形式,如下:

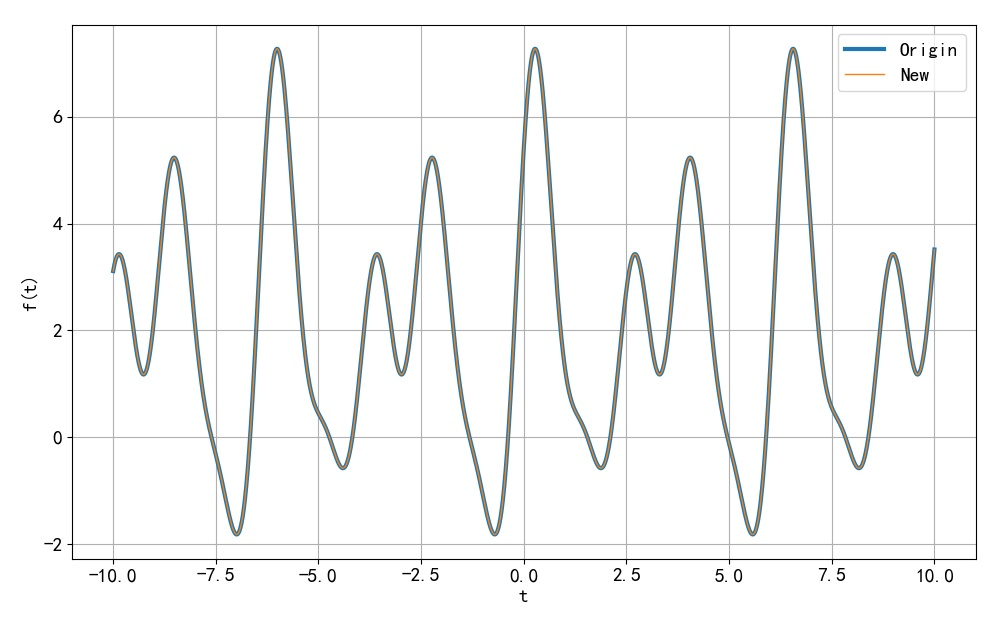
▲ 图1.1.16 题目原来信号表达式与修改后的信号表达式对应的波形根据表达式, 可以知道信号中各个谐波对应的幅度和相角:

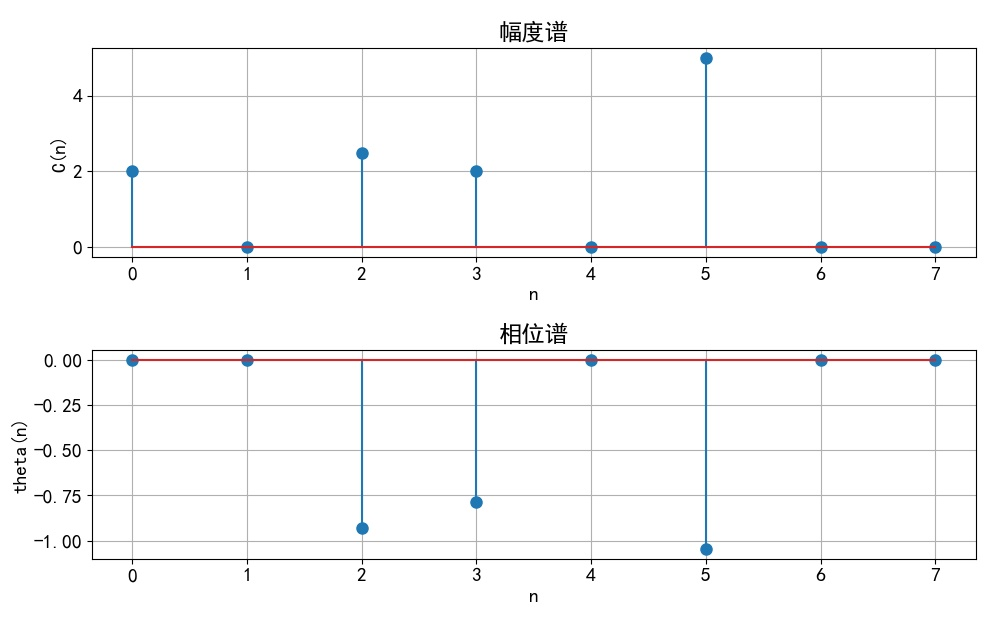
▲ 图1.1.17 信号的单边频谱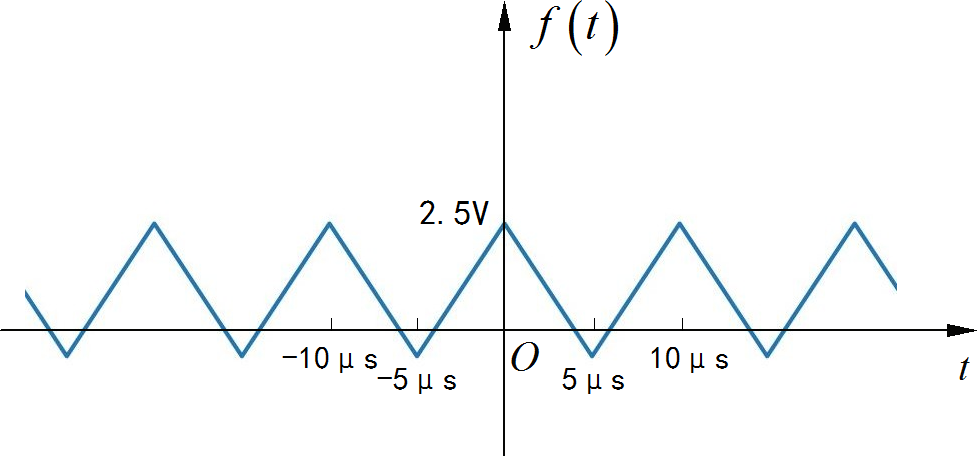
▲ 图1.2.1 电压信号波形◎ 求解:
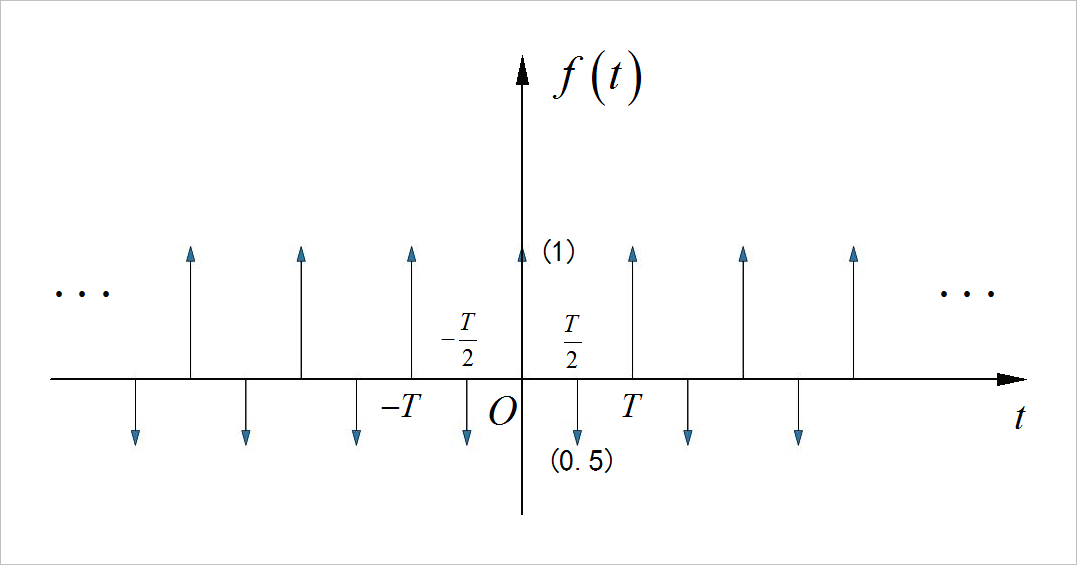
根据观察,信号的周期为 10微秒,对应的基频为 100kHz。信号的交流分量呈现“奇谐对称”,所以信号中只包含有奇次谐波分量,也就是该信号的谐波分量中只有 100kHz, 300kHz, 500kHz。
在给定的四个电路中, 第一个电路为 线性时不变系统, 其余三个都是非线性时不变系统。线性时不变信号的输出信号中不会出现输入信号中 不同的新的频率成分。所以在给定的四个电路中, 除了第一个电路之外,其它三个电路都可以产生 200kHz的谐波分量。
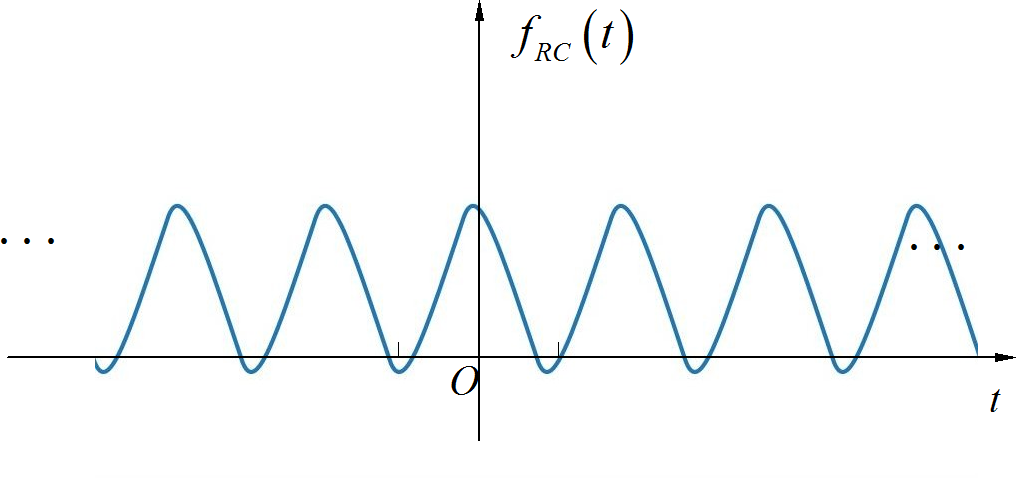
▲ 图A1.2.2 使用SPICE仿真后RC电路输出电压波形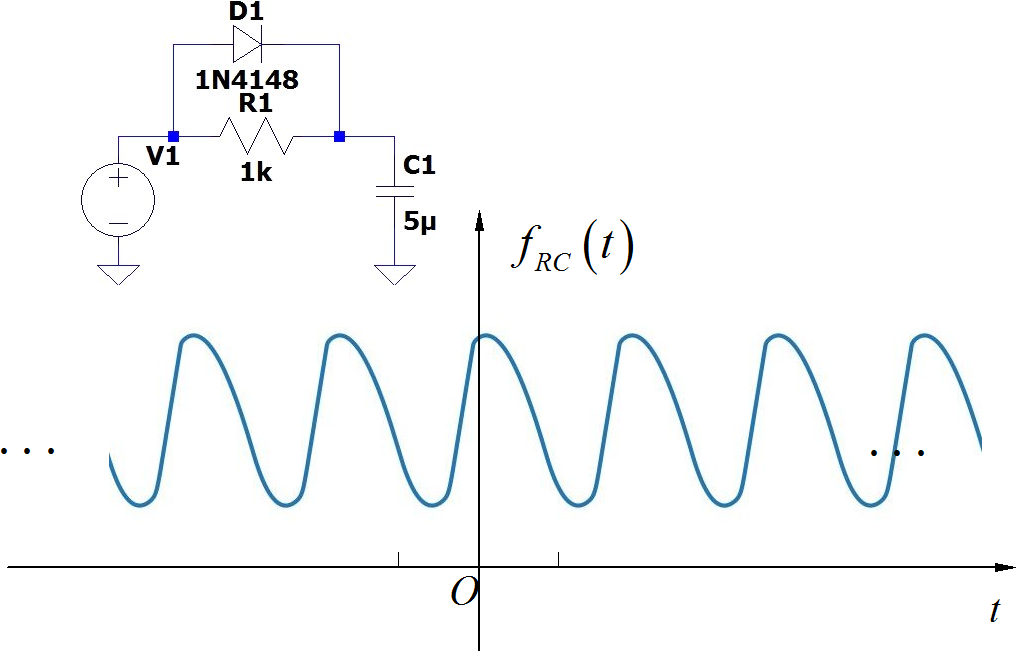
▲ 图A1.2.3 使用SPICE仿真后的二极管RC电路输出电压波形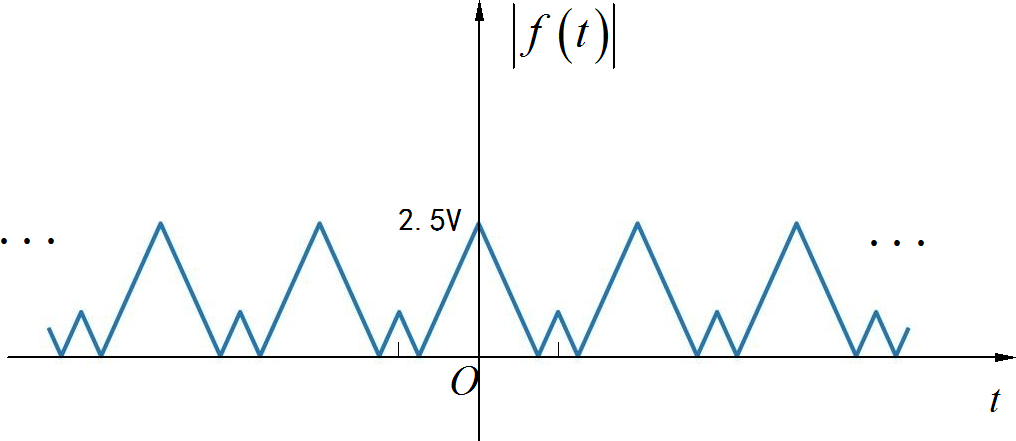
▲ 图A1.2.2 绝对值电路的输出波形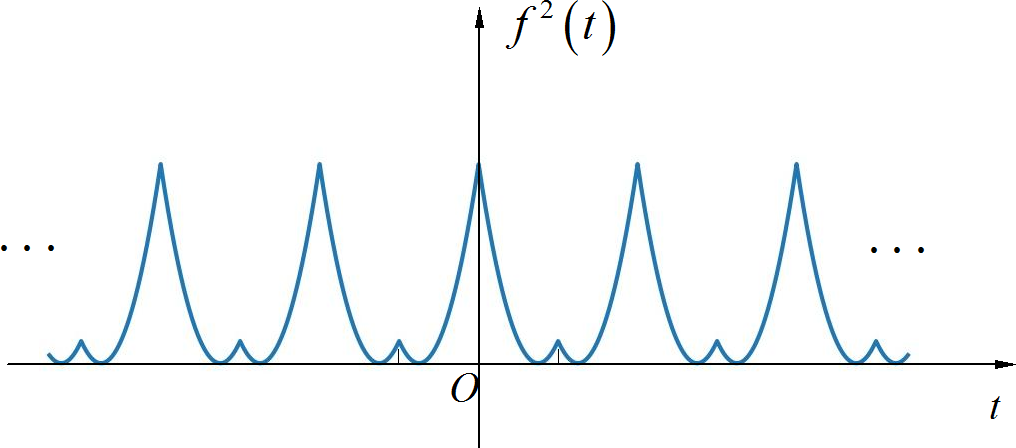
▲ 图A1.2.3 平方电路输出的电路波形◎ 求解:
(1) 根据题目给定条件,信号为偶函数,并呈现奇谐对称。对应的信号波形为:
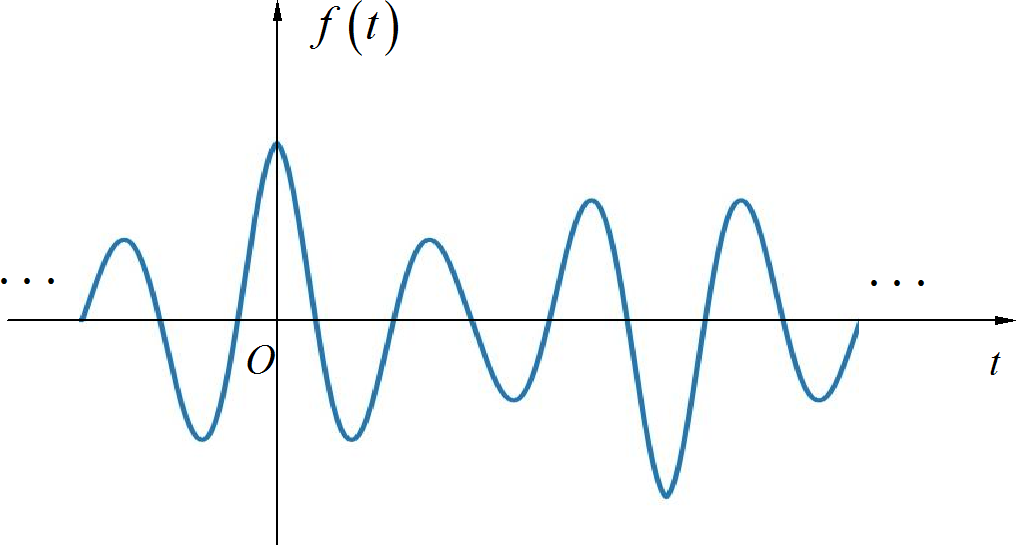
▲ 图1.2.2 补齐后信号在一个周期内的波形(2) 根据题目给定条件,信号为奇函数,呈现所谓的偶谐 对称,实际上就是原来的一个周期内包含两个相同的波形。对应的信号如下图所示:
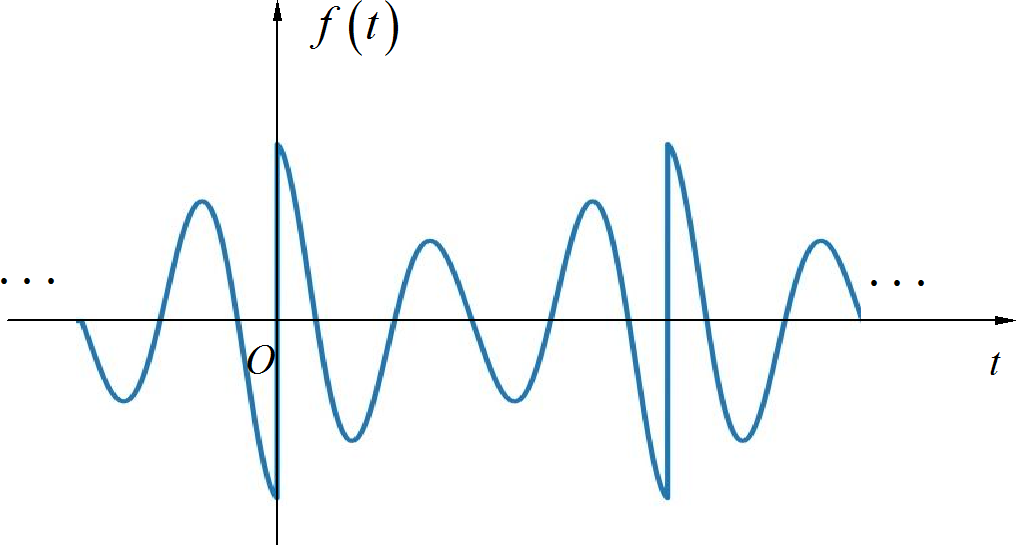
▲ 图1.2.3 补齐后信号在一个周期内的波形
▲ 图1.2.4 个个周期信号中的谐波分量特性◎ 证明:
根据题目可以知道周期信号的周期为 ,那么对应的傅里叶级数为:
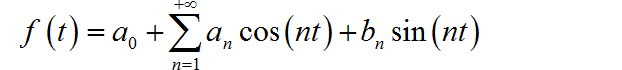
对上面等式两边进行求导:
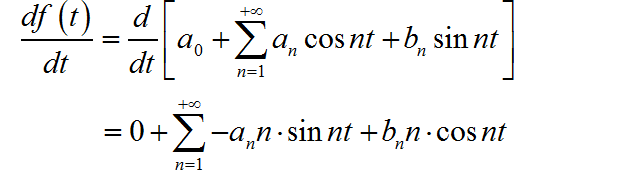
所以,对于 的傅里叶级数 与原来信号的傅里叶级数之间有如下关系:
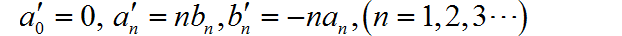

◎ 求解:
根据条件 (1)(2)(3)(4)可以知道给定的函数值包含有一次谐波。根据条件(5)可以知道该谐波的功率为 1/2, 所以该信号的有效值为 , 信号的峰值为 1。
根据条件(6),可以知道该信号为 偶实 信号,所以信号的周期为 6, 峰值为 1 的余弦信号。它的表达式为:

最终,带球的信号参数为:

信号与系统 2023(春季) 作业要求 - 第五次作业: https://zhuoqing.blog.csdn.net/article/details/129729625