说在前面
建立起对计算电磁学更为“体系性”的认知,有助于电磁CAEer站在更高的视角,去审视我们平时所使用的各种电磁CAE软件以及适用于不同计算场景的各类电磁计算算法,这一直是作者期望做但还未做的事,直到作者看到胡俊老师去年在“电波传播年会”上大会报告,回忆不禁被拉回到8年前“计算电磁学”的课堂,“清晰的叙述逻辑、缜密的推理过程、谦逊平和的语调”一直让作者记忆深刻。我想,籍此视频,来给电磁计算方法的发展做一个系统梳理,循着那些计算电磁学巨擘们的研究足迹,了解那段波澜壮阔的历史,应该是一件很有意义的事。

全文的展开主要基于胡俊教授的大会报告以及金建铭教授的著作《计算电磁学(第二版)》。其中胡俊教授的大会讲演视频如下:
金建铭是美国伊利诺伊大学香槟校区(UIUC)电子与计算机工程学院的罗远祉讲座教授,电磁学实验室和计算电磁中心主任,IEEE Fellow。著有《The Finite Element Method in Electromagnetics, Third Edition》和《Electromagnetic Analysis and Design in Magnetic Resonance Imaging》;与他人合著了《Computation of Special Functions》、《Finite Element Analysis of Antennas and Arrays》以及《Fast and Efficient Algorithms in Computational Electromagnetics》被ISI列入论文高引用率的作者名单。作者往期关于计算电磁学的文章也多有参考译本《计算电磁学》一书,全书体系完整、层次分明、文字凝练,可读性较好。


正文
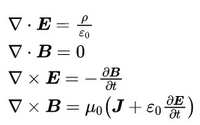
围绕着麦克斯韦方程组的求解,无数科研工作者前赴后继的努力,才有了计算电磁学如今的面貌,发展过程大致可以分为四个阶段:
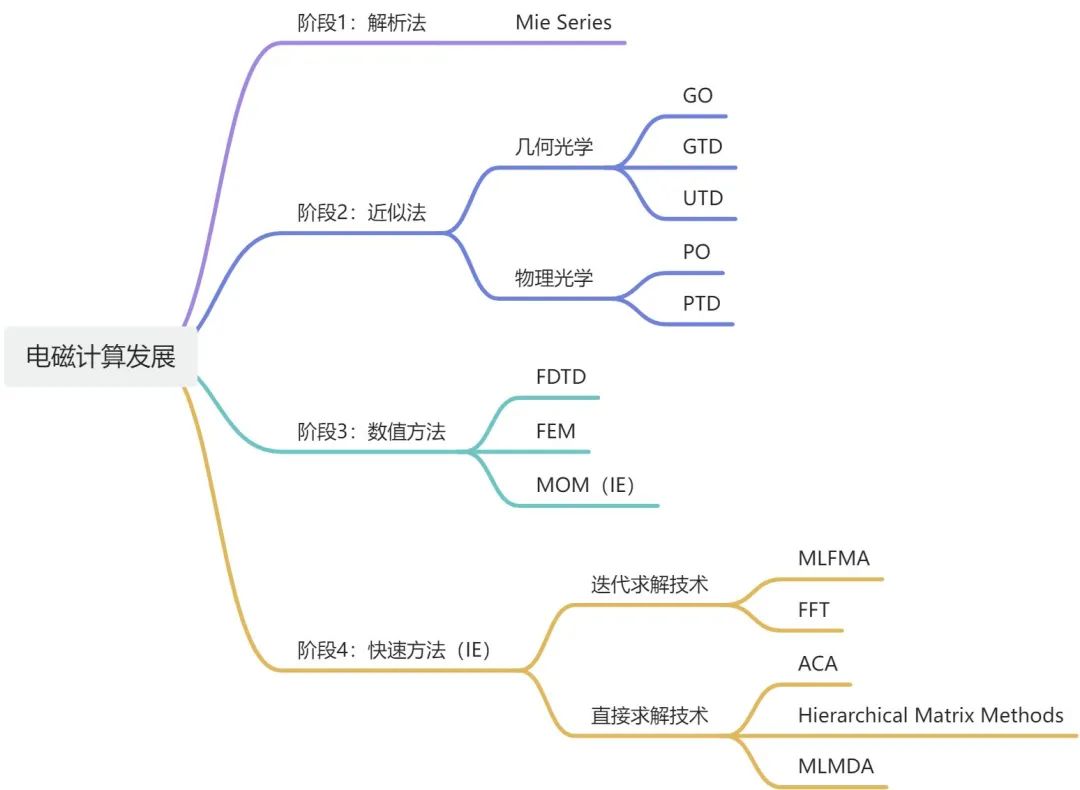
阶段1:解析法
对于结构形式简单的模型,依托高超的数学技能,基于maxwell方程和边界条件,可以计算出空间场分布,即解析解。其优点在于:结果为严格得数学推导,结果完全正确,没有误差,因而可以作为标准去验证各种计算方法得正确性,也常作为RCS测试中定标体,对测试系统进行标定。
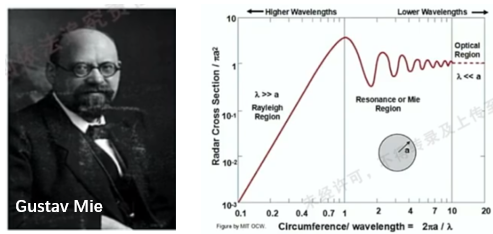

1908年,Gustav Mie 给出了均匀圆球对平面波散射得严格解(Mie理论)。具体理论推导可以参考江长荫于1996年发表在《电波科学学报》上得论文。

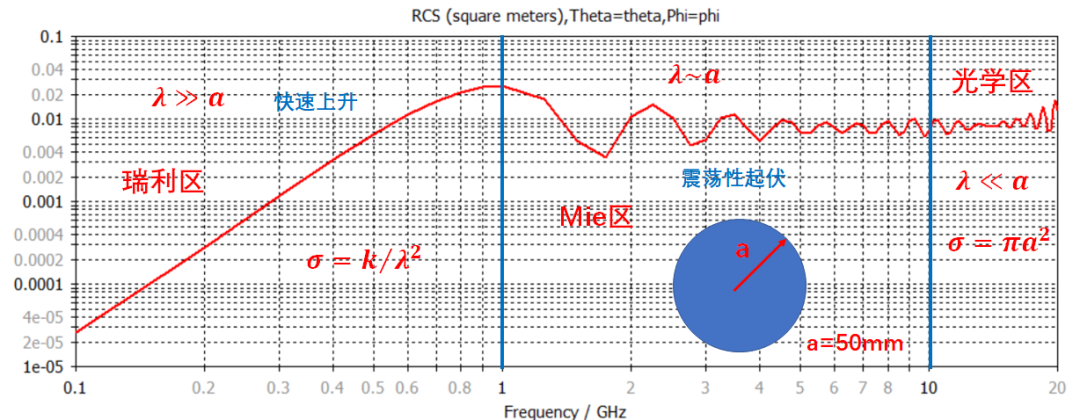
使用CST仿真软件的时域求解器(Transistor),对球的宽带单站RCS进行了计算:取球半径为50mm,计算频率为0.1GHz~20GHz,参考文献对求解结果的分区:1)0.1GHz~1GHz频段内,波长远大于球半径,为瑞利区,此时单站RCS 随频率升高而快速变大;2)1GHz~10GHz频段内,波长与半径相当,为Mie区,单站RCS随频率升高呈现震荡性起伏;3)10GHz~infinity,波长远小于半径,为光学区,单站RCS随频率变化呈现基本稳定。
使用FEKO仿真软件对单频点(10GHz)处金属球的双站RCS进行了计算,其双站RCS的分布形式与往期文章中介绍的阵列天线的方向图有些相似,与感性的认知不同,其最大散射方向并不是后向,而是前向,即与入射电磁波同向。这是不是就是科幻小说《三体》中,使用太阳作为无线电放大器的理论依据,哈哈。
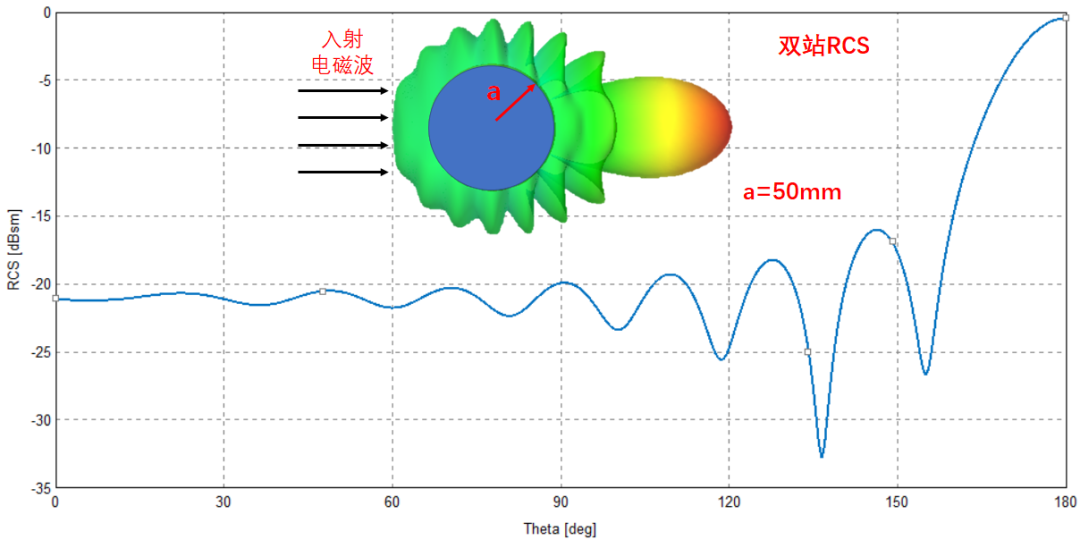
正如往期文章“缘起“收敛性”——Maxwell方程与求解”中所说得那样,形状规则如球形的目标,尚可以借助高超的数学技巧,完成解析计算,但是一旦模型的外形变化一下,复杂的外形所带来的复杂的边界条件,会导致Maxwell方程组无法解析求解。

阶段2:近似方法
在那个“算力”尚不发达的年代,类似“全波仿真”的精确计算方法还没办法被实现,近似方法则因为其较低的“算力需求”而被广泛使用,其中要数几何光学算法(GO)和物理光学算法(PO)应用最为广泛。
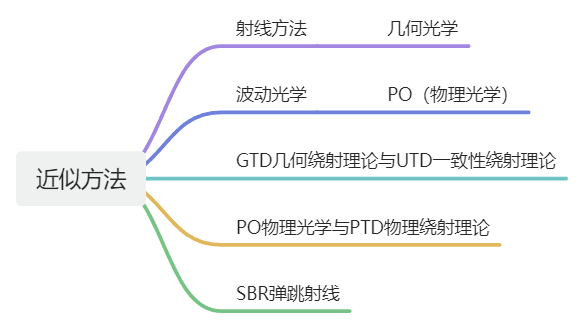
GO(Geometrical Optics几何光学)
几何光学的基本思想基于:高频电磁波的传播近似于光,因而波的传播问题可以采用射线追踪(Ray-Tracing),从而场的振幅可以根据波前表面的形状来确定。显然,使用几何光学方法,阴影区域中的场完全为零,而被照亮区域中的场为单独的入射场或入射场与反射场的叠加。物体边沿和尖劈的衍射场被完全忽略,而总场有两处具有非物理的不连续性:一处是在亮区和阴影区之间的边界(称为入射阴影边界,ISB),另一处是在反射区和反射不能到达的区域之间的边界(称为反射阴影区,RSB)。
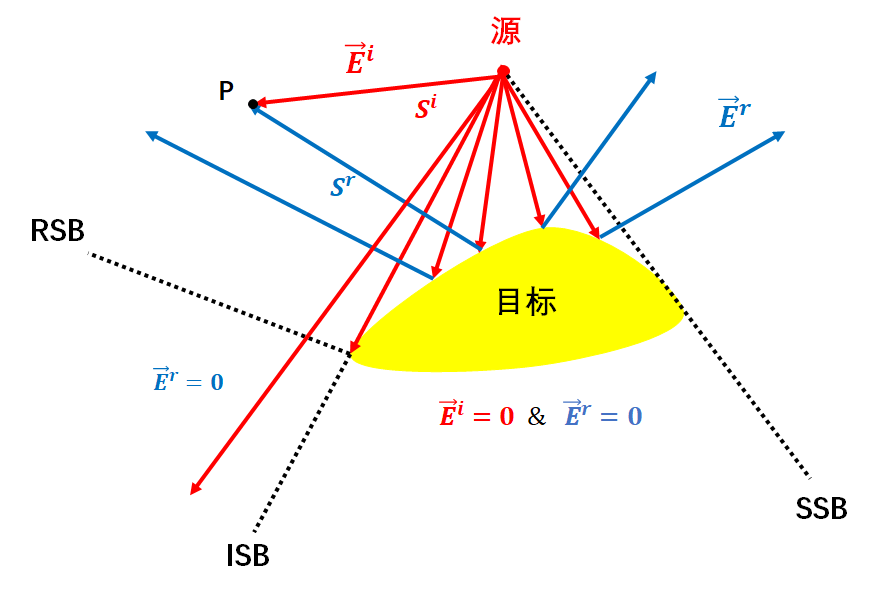
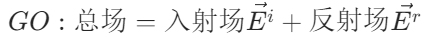
其中入射场和反射场可分别由下列公式求得:
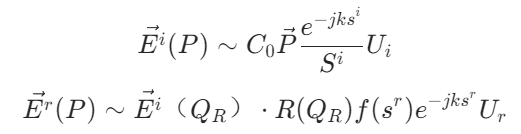
入射场和反射场是否被置零则取决于系数和的取值:
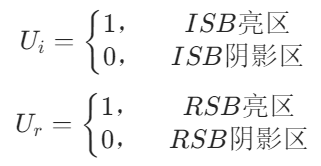
GTD(Geometrical Theory of Diffraction几何绕射理论)

我们可以在几何光学的解中加入衍射场以提高几何光学解的精度,由此产生了几何绕射理论(GTD)。GO的修正绕射线产生于结构不连续处和材料不连续处,以及电磁波掠入射光滑凸表面情形,主要有以下集中类型:
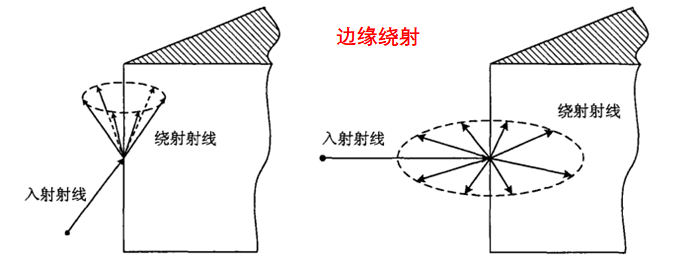
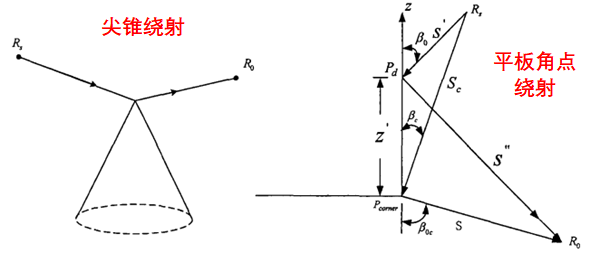
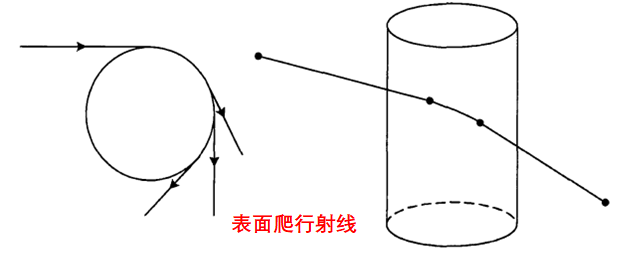
UTD(Uniform Theory of Diffraction一致性绕射理论)
Keller导出的GTD理论,在亮区和阴影区的边界两侧的过度区失效,如图所示,以无限长导带的散射为例,按照GTD理论,则会在两个边界处产生无穷大的散射场,与客观事实不相符,而UTD则会通过比例系数的引入,将过渡区的场控制在一个有限大范围内,具有更高的计算精度。
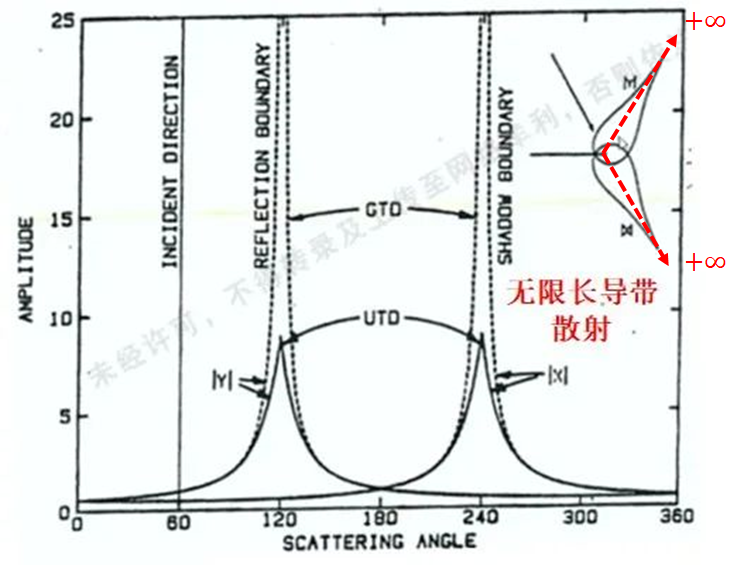
PO(Physical Optics物理光学)
另外一类高频近似技术从物理光学(PO)出发,将电大尺寸导体亮区表面上的感应电流密度近似为,而阴影区的电流密度近似为。进而自由空间中的场分布可以依据源-场关系求得:

物理光学算法被广泛应用于反射面天线辐射特性的计算,馈源使用全波算法,反射面使用PO算法,两种算法混合,从而使得电大尺寸的反射面能够快速获得相对准确的计算结果。
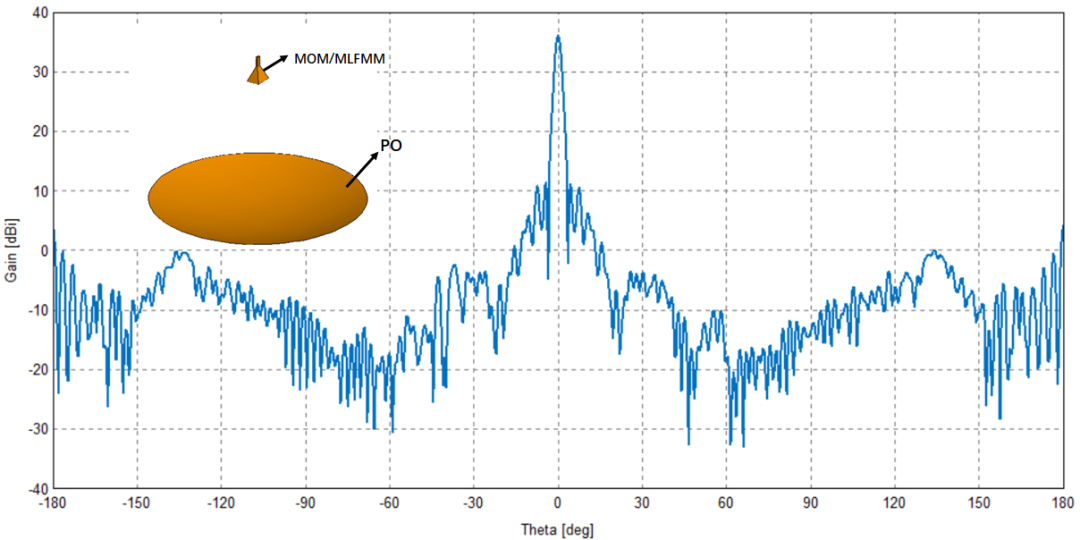
PTD(Physical Theory of Diffraction物理衍射理论)
物理光学理论(PO)近似忽略了几何不连续性对感应电流的影响,因此近似的感应电流在亮区和暗区边界处存在不连续,这种不连续影响了计算结果的精度,通过在感应电流中加入非均匀的边缘电流,以此来改善物理光学的计算精度。这一思想导致了物理衍射理论(PTD),详细可以阅读Petr Ufimtsve教授的著作《Fundamentals of the Physical Theory of Diffraction》。

后来闻名世界的第一款隐身战斗机F-117的隐身设计正是基于此理论而完成的设计。

SBR(shooting and bouncing ray弹跳射线算法)
将几何光学与物理光学的方法结合起来,开发出了功能强大的算法,用于计算大尺寸复杂目标的电磁散射,这种混合技术称为弹跳射线(SBR)法。在该方法中,从源出发的入射波用指向物体的射线簇表示。当每条射线反弹时,其相关的振幅和相位均被追踪,而反弹过程受几何光学的约束。在射线与目标的每一个交点应用物理光学法做积分,以确定射线对散射场或辐射场的贡献,最终解是所有射线贡献的总和。这种算法已经被实现并广泛用于计算雷达散射特征、大型平台上天线的辐射特性和复杂城市环境中的电磁波传播。
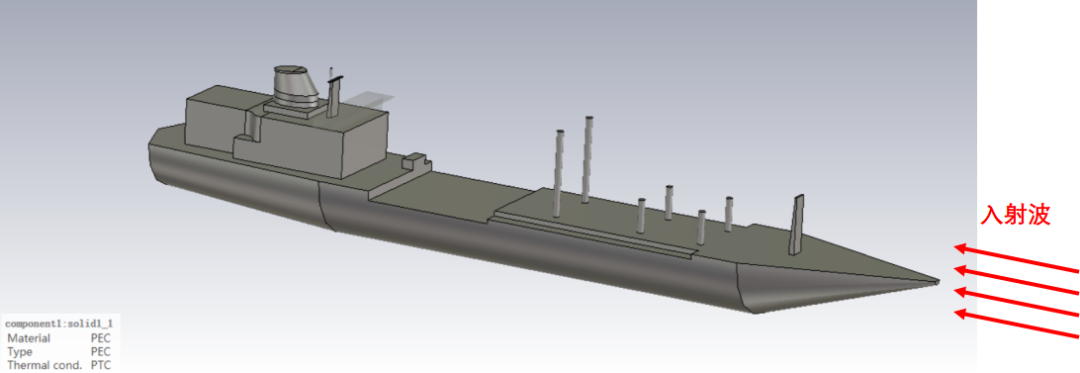
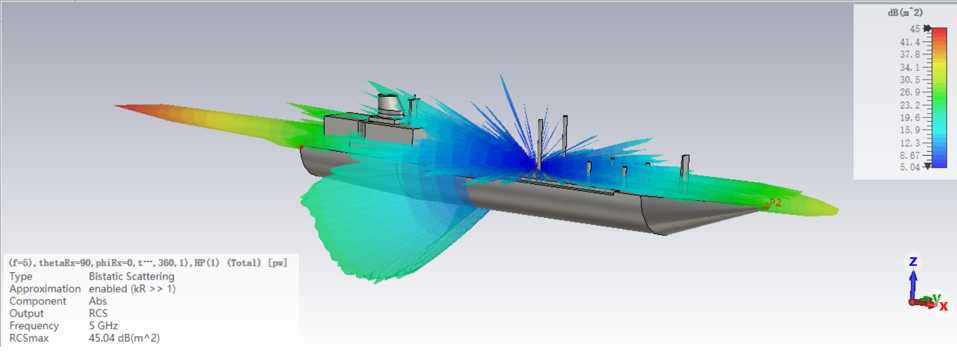
依托CST软件的Asymptotic Sovler(渐进求解器)的SBR算法,使用个人笔记本(8GHz内存)即可完成电尺寸达200倍波长的缩比舰船模型的散射特性的计算,计算效率可以说相当之高。
阶段3:数值方法阶段
随着电子计算机“ENIAC”的诞生以及其后“计算能力”飞速发展,基于“数值计算”的全波分析方法也迎来了爆发式发展。其中要以时域有限差分算法(FDTD),有限元算法(FEM)以及矩量法(MOM)发展最为完备,成为三种最主流的电磁数值计算方法。
FDTD(时域有限差分):

1966年,加州大学伯克利分校的Kane S. Yee教授发表了基于交替网格的有限差分求解Maxwell方程的论文,1980年,该方法正是被命名为FDTD,全文的被被引用次数高达8000次。其离散的对象直接是时域微分形式的Maxwell方程组:
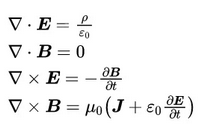

FDTD所使用离散形式也是最为简单的立方体网格,每一个立方体网格就是一个Yee元胞。
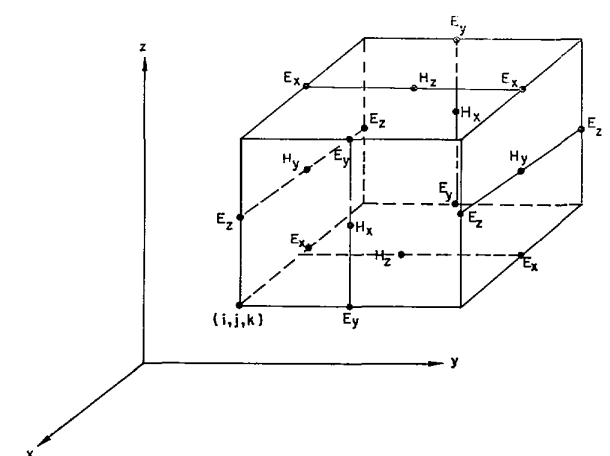
每个元胞上的电场和磁场可以分解为直角坐标系下的三方向分量、、以及、、,上述矢量形式的Maxwell方程即可以展开为标量形式的maxwell方程:
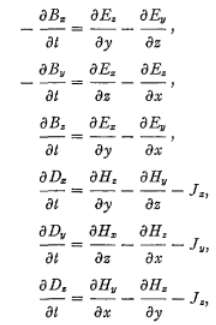
由标量形式方程可知,方程中包含了对电场和磁场分布函数的时间微分运算以及空间微分运算,以电场为例,其中表示对时间的微分运算,和表示对空间的微分运算,其中和最终均可以拆解为,,的组合,这四种微分运算可以用这种通用的表达式进行描述,其可近似为一种简单差分形式:
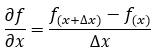
利用这个近似运算,可以将电场对时间的微分运算转换成前一时刻的电场与后一时刻电场之间的运算关系。同样地电场E对空间微分运算转换成前一位置处的电场与后一位置处的电场之间的运算关系 ,因而只要给定了电磁场的初始值和(初始条件)以及边界值和(边界条件),即可以基于差分关系式,通过不断的循环迭代,求解出任意时刻,任意位置处的电磁场分布和和。
想要深入学习FDTD知识的读者,可以阅读IEEE Fellow、美国西北大学教授Allen Taflove的教材《Computational Electromanetics:The Finite-Difference Time-Domain Method》,该教材位于《The Electric Engineering Handbooks》(见附件)的第629~670页。

MOM(矩量法):
矩量法的的基本数学概念最初在20世纪初被提出,直到20世纪60年代中期,随着K. K. Mei教授等研究人员将其引电磁学的数值计算,才逐渐被大家广泛关注,1968年,Harrintong教授在其开创性的专著《Field Computation by Moment Methods》中对矩量法进行了统一阐述。此后,矩量法得到进一步发展,并被广泛用于求解各类重要的电磁问题。


FDTD和FEM的统治方程均基于微分形式的Maxwell方程,其特点为:1)其通过直接求解“场”(电场或磁场)满足的方程来获得空间电磁场的分布;2)求解对象为“微分形式”的Maxwell方程。而MoM则基于一种完全不同的求解思路。
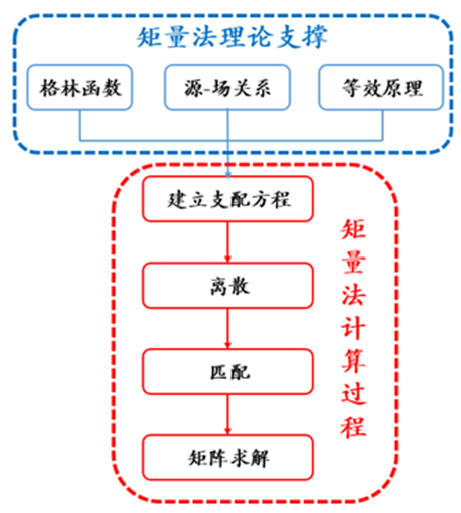
MoM算法理论主要分为两个部分:一个是矩量法支撑理论,主要包括“格林函数”,“源-场关系”,“等效原理”三个子理论,它们是MoM算法如此特立独行的根本原因;另一个则是矩量法计算理论,主要包括四个步骤:建立支配方程—>离散—>匹配—>矩阵求解,这与FEM或FDTD算法的求解过程并无明显区别。详细的推理过程,作者在往期文章“CAE设计师的你,有必要了解计算电磁学吗?”中已做了详尽展示,此处就不在赘述。
FEM(有限元):
1969年,P. P. Silvester使用有限元方法分析了空心波导中波的传播,这是有限元方法第一次被应用于微波工程和电磁学中。

有限元法基于频域Maxwell方程,其求解的对象是时谐电磁场,即电磁场在时间维度上是周期性分布,循环往复,无始无终,时间变量自然也就失去了意义,电磁场只是空间变量的分布函数:
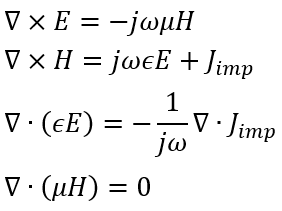
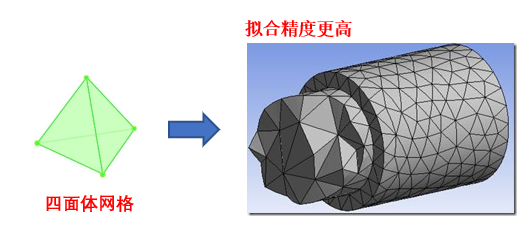
其采用了拟合效果更好的四面体网格对求解区域体进行剖分。
求解空间离散后,紧接着是要空间中待求解的电磁场分布进行离散,其核心思想在于寻找到一组展开未知解的基函数:
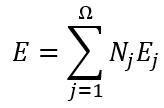
其中为第j条棱边的切向分量,为待求的切向分量,而为相应棱边上对应的基函数,一旦将所有未知量求解出来,则整个空间中电场分布就完成了求解。这类似于傅里叶级数中使用三角函数展开任意形式的周期函数,所要做的就是求解每个基函数前面系数,然而对于形状不规则的电磁问题,这种基函数的寻找是及其困难甚至不可能的,有限元法的做法是将目标离散成小的单元(三角形,四面体),然后使用非常简单的线性函数或二次函数来近似这个单元上的未知解,这些简单的基函数是一种子域基函数,其与上文中傅里叶级数展开中的全局基函数有着很大的不同。利用有限元将目标离散,并依据电场E在空间Ω满足的波动方程和在边界Γ上满足的边界条件条件建立子域基函数的系数所满足的方程组:
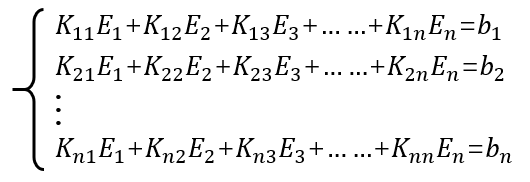
该方程未知量为子域基函数的系数,完成所有未知量的求解,整个空间的电场分布既可以表示为子域函数的叠加。
想要深入学习FEM算法的读者,可以进一步阅读金建铭教授的著作《The Finite Element Method in Electromagnetics》或John L. Volakis教授的著作《Finite Element Method For Electromagnetics》。


阶段4:快速计算
传统的数值方法(FEM/FDTD/MOM等)精度高,但对于复杂电大尺寸目标,离散需要的未知量数目多,计算存储巨大,效率低。高频近似方法(GO/GTD/UTD/PO/PTD等)存储量要求低,计算速度快,但是精度难以满足要求。
寻求精确、高效的数值建模方法是计算电磁学领域高度关注的重要课题,直到世纪之交,快速算法的的出现以及后面的迅猛发展,大大降低了计算的复杂度和存储量。由于胡俊教授所在的电子科大电磁辐射/散射研究团队研究重点聚焦于“积分方程方法”,因此大会报告中关于“快速算法”的一些进展主要围绕“积分方程展开”。积分方程方法的主要特点为:
基于格林函数:自动满足远场辐射条件,无需设置吸收边界条件,没有网格截断误差;
等效电流/磁流作为待求未知量:分布在目标表面(导体/均匀介质)或目标体内(非均匀介质);
阻抗矩阵元素精确计算难题:奇异性、近奇异性积分数值计算;
全局耦合:不同于微分方程产生的稀疏矩阵,积分方程方法导致稠密矩阵,带来较高的计算复杂度和存储量;
快速算法按照求解方法可以分为迭代求解技术和直接求解技术,其中迭代求解技术速度更快但是处理病态矩阵会存在不收敛的问题,直接求解技术不存在收敛性的问题、且适合处理多右端项问题。
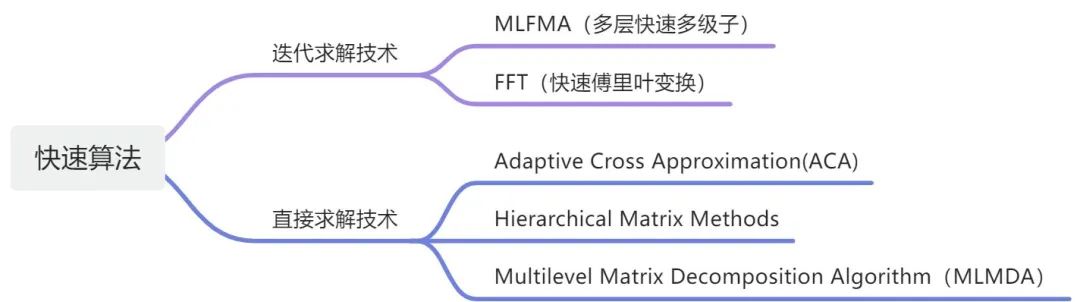
FMM(快速多级子):
FMM(快速多级子算法)最初由耶鲁大学的Rokhlin教授提出,用来快速求解粒子间的相互作用和静态方程。后来被周永祖(W. C. Chew)教授引入计算电磁学,极大的降低了计算复杂度和内存消耗,其后,国内的聂在平教授带领的团队独立在该领域率先取得突破。



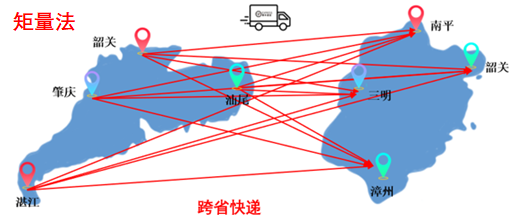
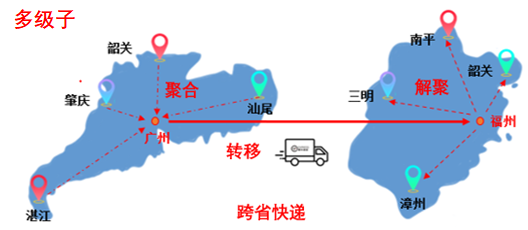
在矩量法中,矩阵向量积的计算可以等效看成计算许多电流元的自作用和互作用,即计算每个电流元所辐射的被所有电流元接收到的场。快速多级子基于这样的基本思想:首先根据电流元在空间中的位置将其分成若干组,每一组为相互邻近电流元的集合,然后基于加法定理,将组内不同电流元从不同中心发出的辐射场变换成一个共同中心辐射的场。
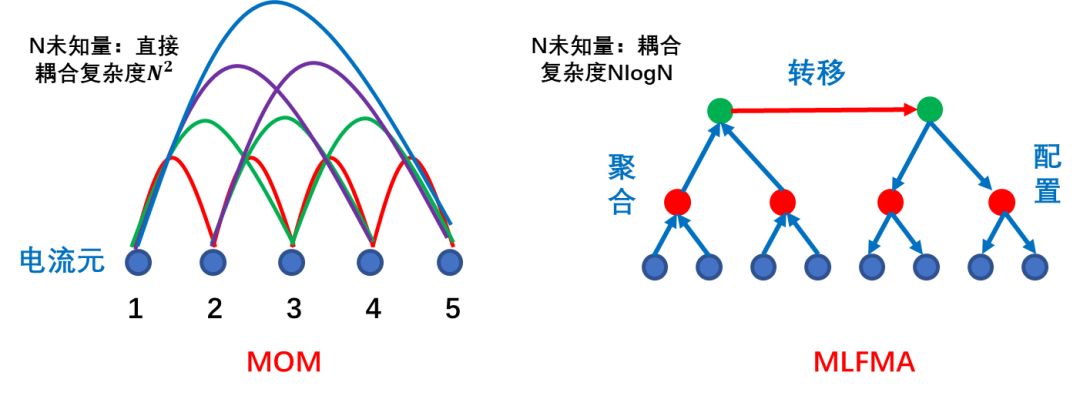
通俗的理解,可以参考往期文章“CAE设计师的你,有必要了解计算电磁学吗?”中“跨省快递”的类比,由图可知:快速多级子算法极大的降低单元之间耦合的计算量。
CG-FFT(共轭梯度-快速傅里叶变换):
历史上第一个为计算电磁学开发的快速算法是共轭梯度-快速傅里叶变换法,因为其简单性,这种方法至今依然是最有效的快速算法。算法的核心思想是将矩量法的矩阵分解成近相互作用和远相互作用两个部分,这一思想与后来的快速多级子具有相同的核心思想。
有关共轭梯度-快速傅里叶变换算法(CG-FFT)的更加深入的数理推演,受限于作者目前的认知水平和精力,只能暂时先留下相关学习著作和参考文献,以备后续深入学习之需要,互勉。

以上简单介绍了基于迭代求解技术的两种快速算法,有关直接求解方法等更多关于“快速算法”研究方向的读者,可以进一步阅读2013年《Proceedings of The IEEE》杂志第二期关于“快速算法”的专刊,其中系统就快速算法的研究现状进行了讨论和展示,文末附件摘取了部分文章以供阅读。

延申:基于积分方程方法的一些最新进展
由于胡俊教授所在的研究团队主要致力于“积分方程方法”的研究,因此电磁计算目前最前沿的研究“引申”也主要围绕积分方程方法(IE)展开。
随着电磁计算方法应用的日益广泛,所要面对的求解问题也越来越复杂,复杂目标电磁建模面对的困难主要分为以下几个方面:
目标由介质/金属组成,多媒质问题;
细微于宏观结构并存,多尺度问题;
目标电大尺寸/超电大尺寸问题;
散射强度较低(隐身),计算精确性要求高;
多尺度多媒质目标计算的收敛性差;
围绕这些问题,主要的研究思路有:1)发展区域分解方法;2)发展直接求解器......
DDM(Domain Decomposition Method区域分解算法)
2013年,IEEE Fellow、俄亥俄州立大学教授Jin-Fa Lee的学生Zhen Peng发表了题为《A Discontinuous Galerkin Surface Integral Equation Method for Electromagnetic Wave Scattering From Nonpenetrable Targets》,并于次年获得“谢昆诺夫最佳论文奖”,带动了一股积分方程区域分解方法(IE-DDM)的研究潮。
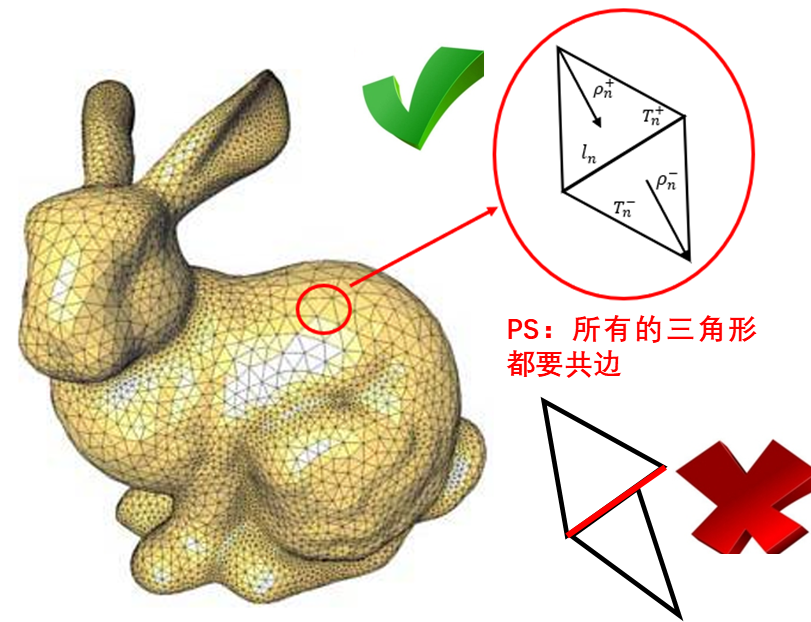
传统积分方程方法(Integral Equation),如我们在FEKO仿真软件中使用的矩量法(MOM)或基于其上改进的多层快速多级子算法(MLFMM),由于需要保持剖分网格在棱边上不会产生电荷积累,因此对网格的要求是一定要共形,即所有的剖分单元都要共边。这也有就是为什么使用FEKO对相接触的模型进行剖分时,必须要union,以确保相邻模型会一体化剖分,维持共形条件。
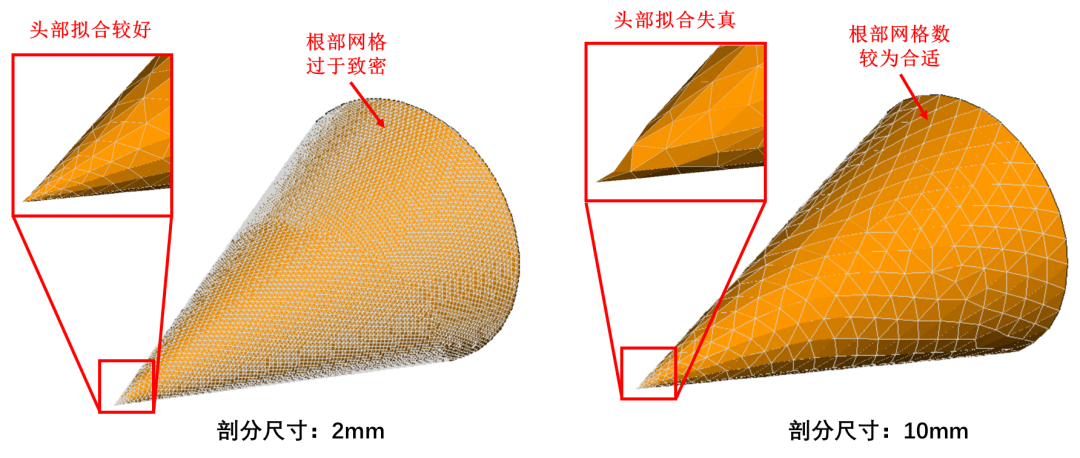
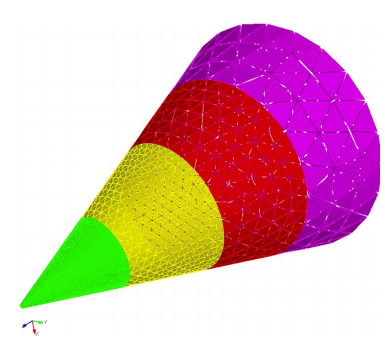
网格共形的要求对于处理一些类似于“多尺度问题”时(同时包含有精细结构和平坦结构),则会遇到较大麻烦:如下图所示的尖锥模型的剖分示意图,如果需要较好的拟合头部(精细结构)形状,则剖分尺寸较小,根部平坦区域的网格则显得过于致密,网格数量多,如果按照根部平坦区域去设置剖分尺寸,则网格对于头部区域的拟合则会出现的失真现象,影响计算精度;同时,网格尺寸在模型表面过快的增长也会带来矩阵性态的恶化,从而导致收敛性变差的问题。
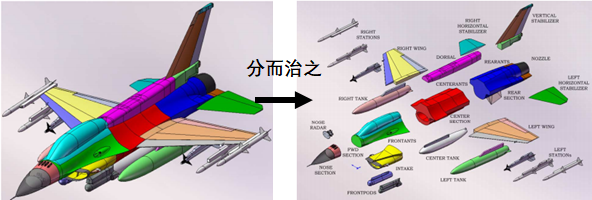
IE-DDM的思想就是按照模型的精细程度进行分类,不同区域按照不同的剖分尺寸进行进行剖分,分别计算,分而治之。其主要克服的难点就在于解决网格不连续处的电荷积累问题,具体的理论推演可以阅读Zhen Peng的原文,这里就不作展开了。
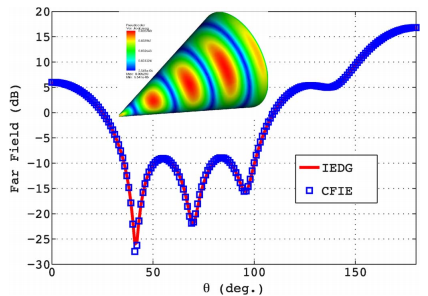
文中,作者挑战了一个包含天线罩、机载天线、进气道、挂载武器等多种令积分方程较为头疼部件的F-16战斗机整机的的电磁计算问题。分别计算了战机在3GHz和10GHz频率下的表面电流分布。

Directive solver(直接求解方法)
围绕着“积分方程”方法,发展了两种求解思路,一种类似于上文中所提到的共轭梯度-快速傅里叶变换算法和快速多级子算法的迭代求解方法。这类方法计算速度快、内存消耗小,针对绝大部分电磁计算问题,不失为最优选择。但是不太适用于以下情况:
病态矩阵系统(强谐振、多尺度结构)
多右端项问题(单站RCS、不确定性量化)
系统部分更新(逆散射问题、闭环优化)
遇到这些情景时,高效的直接求解算法可能成为更好的选择。直接求解方法围绕散射矩阵,直接开展计算,因此不存在收敛的问题,且对于多右端项问题,只需计算一种状态,其余状态即可快速给出,因此状态非常多时,也不失为一个好的选择。
高效的直接求解算法,则是针对“传统直接求解算法”矩阵计算速度太慢、内存消耗太大的问题而开展的,一般基于低秩压缩,主要方法有:
详细的介绍,由于并不是作者了解的领域,暂时不做展开,留下一些相关参考文献,以备后续深入学习。

总结

声明:
投稿/招聘/推广/宣传 请加微信:15989459034
