迭代解卷积的不稳定性

01 解卷积

一、解卷积

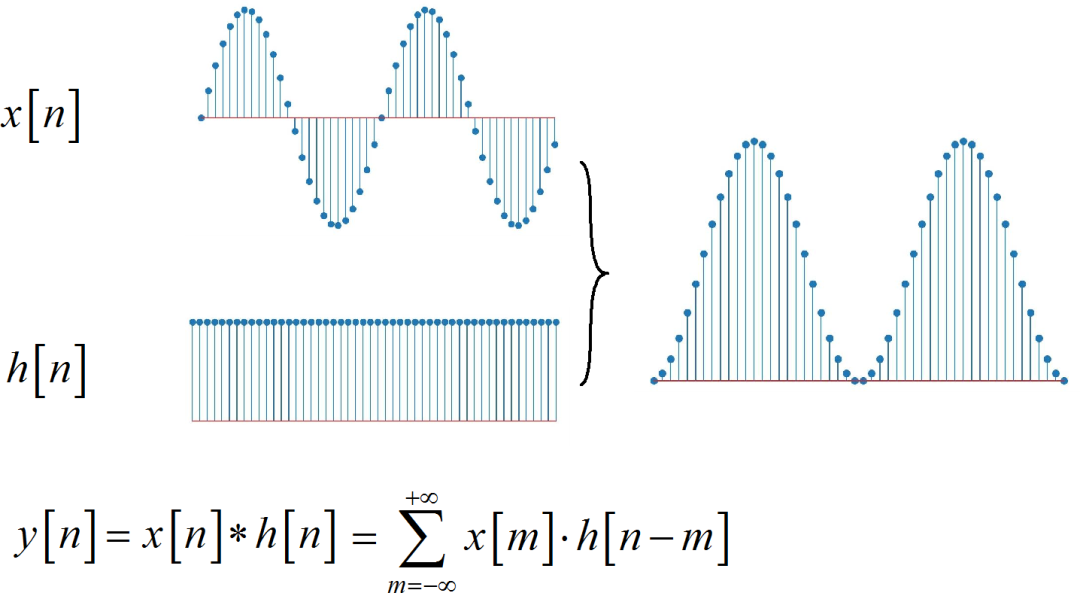
  已知两个序列， 分别是 x[n] 以及 h[n]， 它们之间的卷积  定义为这样的累加和。 是将其中一个序列进行反褶、平移、再与另外一个序列相乘、累加， 最终得到卷积结果。  如果已知卷积结果和其中一个序列， 求取另外一个序列的过程，  称为解卷积。

  如果两个参与卷积的序列 都是因果序列。 那么累加的上下限就变成从 0 到 n。  然后再将该累加公式 分成两项。  进行化简之后，便可以得到关于 x[n] 的迭代公式。  将 h[0] 移到方程左边， 每一次迭代就可以得到最新的 x[n] 的数值。     下面讨论一下这个方程在噪声情况下的特性。 

二、加噪声解卷积

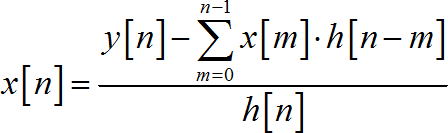
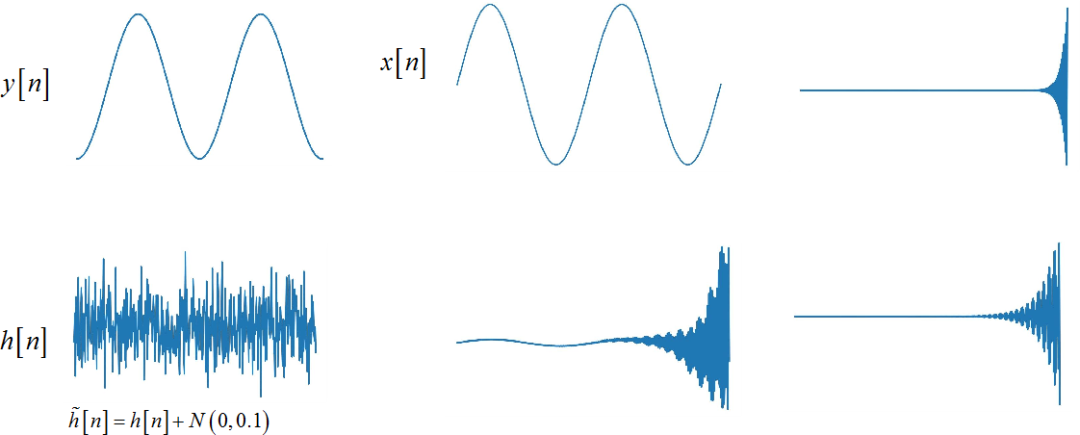
  为了展示解卷积，  还是利用前面的正弦信号的卷积作为例子。 这里假设已知 y[n],h[n]，求解 x[n]。 为了展示迭代噪声的影响，这里将序列的密度增加， 这是 500 个数据点形成的 x[n] 序列，  将 h[n],y[n]对应的序列的采样密度也增加。 下面应用这些数据进行解卷积。

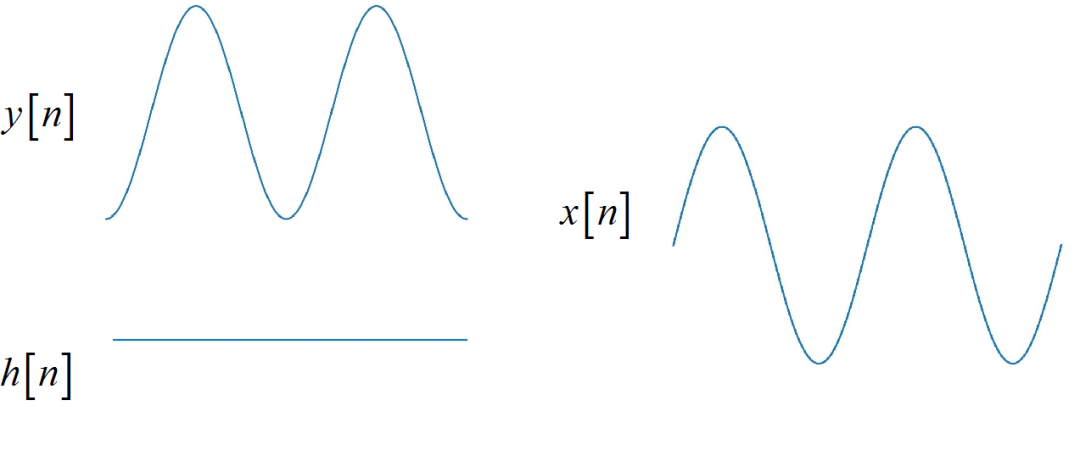
  下面通过 Python 编程， 实现其中的解卷积公式， 从给定的两个序列获得解卷积结果。 这是从 y[n],h[n] 中计算 x[n] 的取值， 可以看到与原来的 sine 波形是一样的， 证明了解卷积公式和子程序的正确性。

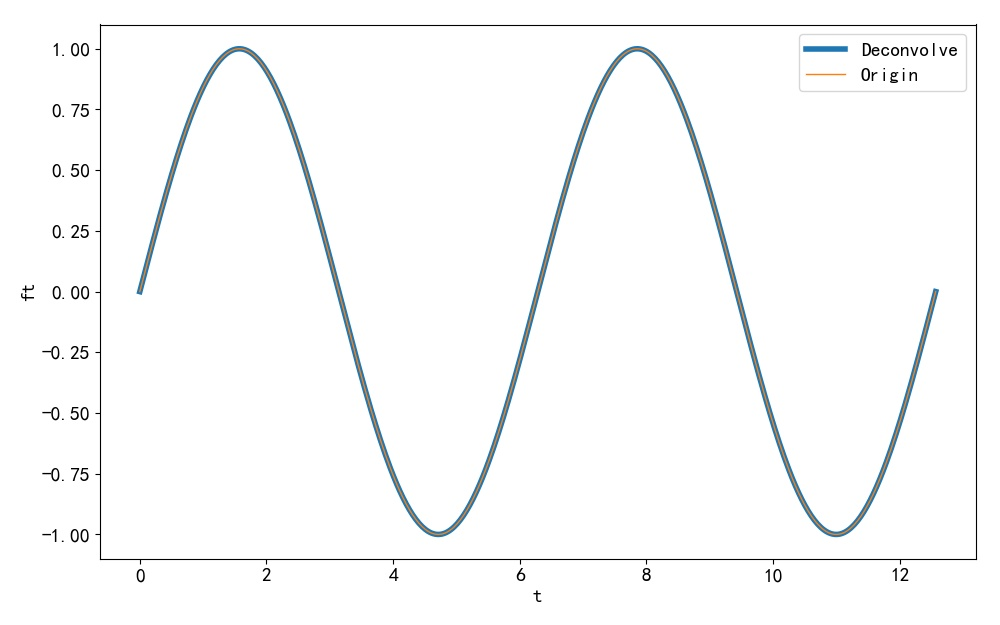
  首先在卷积结果上增加正态分布的白噪声， 噪声的方差为 1。 利用卷积公式求 x[n]， 可以看到求解出的 x[n] 波形中也增加了白噪声， 方差大约为 1。 将 y[n] 中的噪声方程减小到 0.1， 求解得到的 x[n] 的噪声 也减少了。特别是，这个结果中的噪声似乎并没有随着 n 的增加呈现累积增加的倾向。

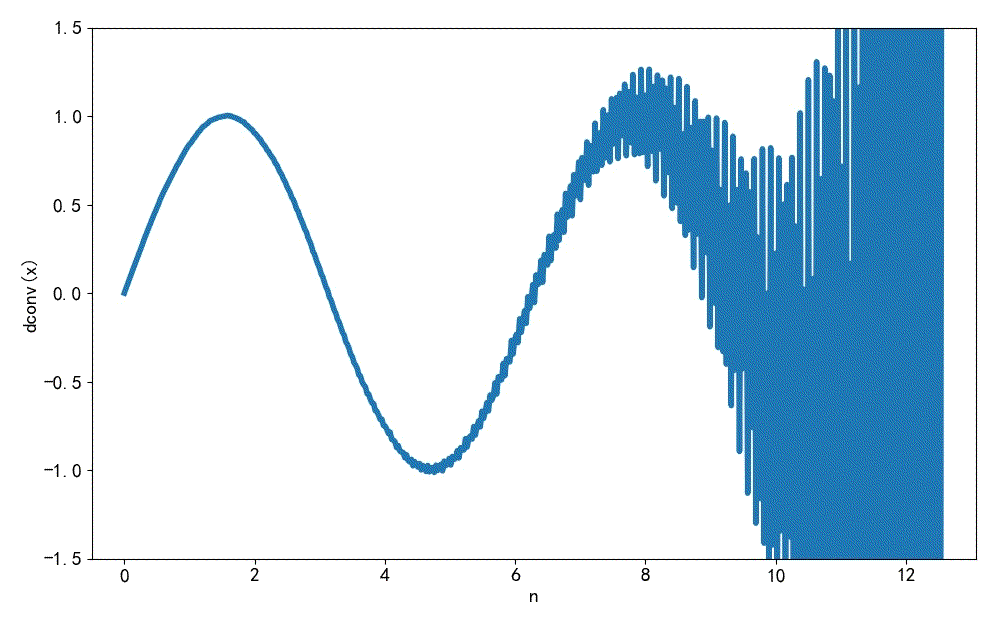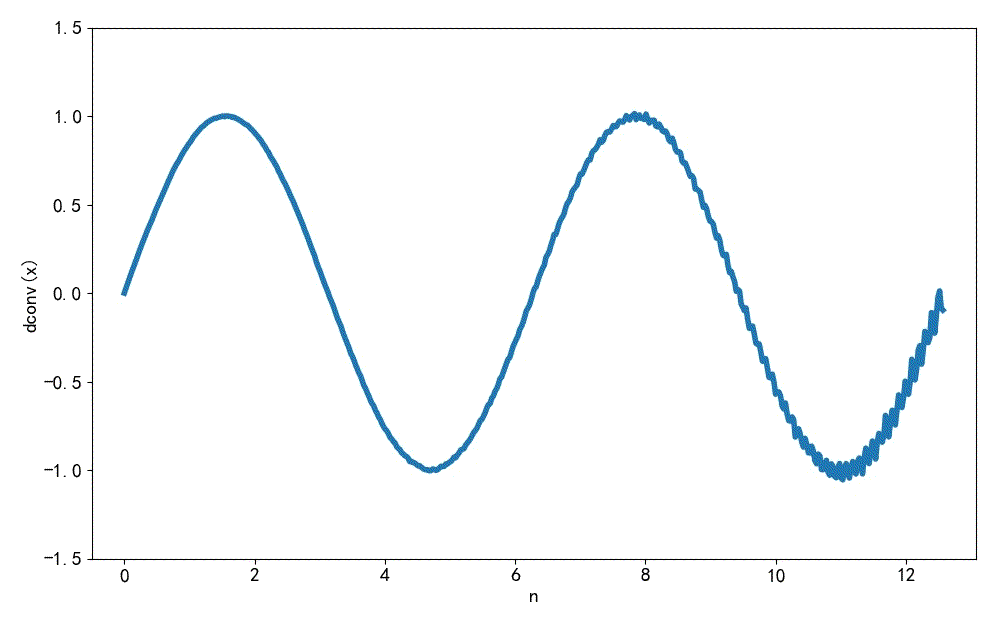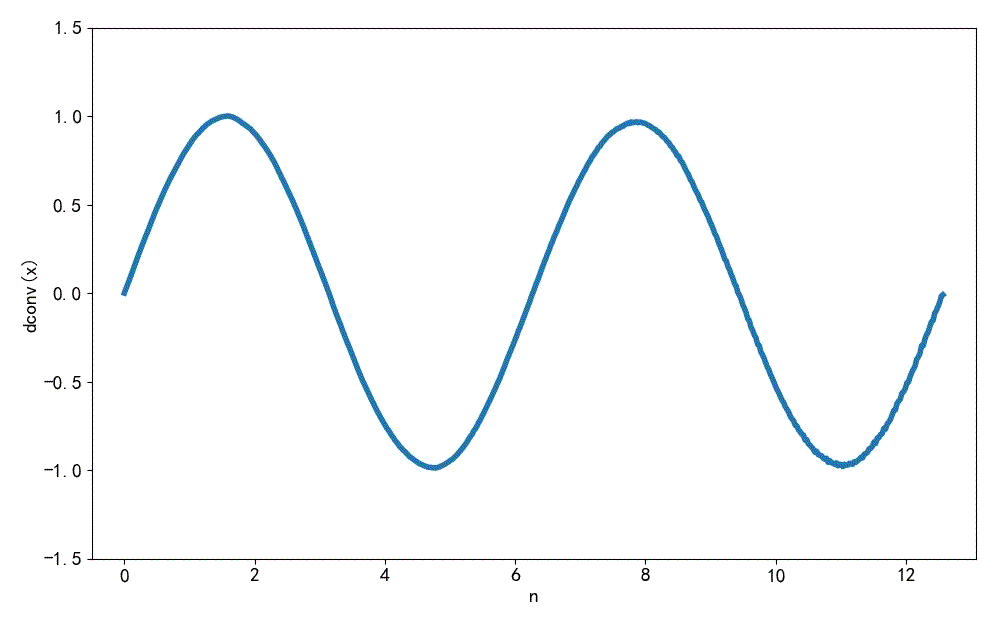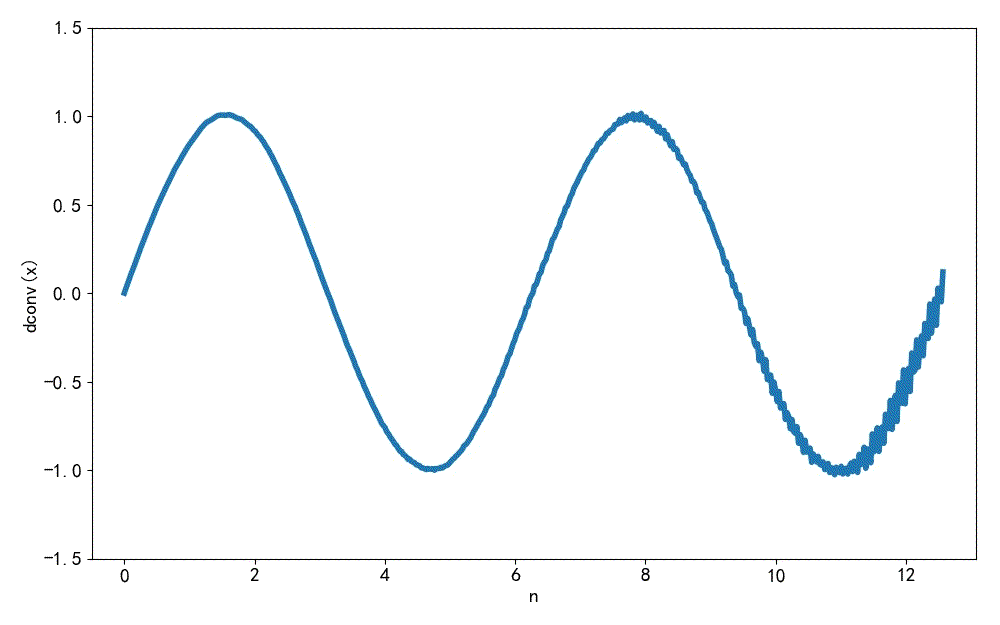
  下面在参与求解的 h[n] 中增加噪声， 随机噪声的方差为 0.1，  大约是 h[n] 幅值的 10% 左右。 这是求解之后的 x[n] 的取值， 似乎 x[n] 已经发散了。 这是另一次运行结果， 与前面求解 x[n] 有所不同， 这是第三次运行的结果， x[n] 结果仍然是发散的趋势，  可以看到这种迭代解卷积对于 h[n] 中的噪声比较敏感， 而且每次运行结果还都是不尽相同。 这是在 h[n] 中叠加上 10% 的高斯噪声的测试结果。

  下面将 h[n] 的方程  减小到 0.05。 对 x[n] 进行解卷积， 这是解卷积 30 次形成的结果， 可以看到这种解卷积的结果不是很稳定， 特别是随着 n 增加，后面结果中的误差会累积，直到出现发散。 这个测试验证了这种迭代解卷积的方法在数值上不是很稳定。

※ 总  结 ※

  本文对于迭代方法求解卷积进行测试， 可以看到在参与卷积数据中存在噪声时， 迭代方法求得结果中的误差会出现累计， 结果也呈现发散的倾向。