给大家展示一下如何使用ChatGPT和一个优秀的猪脑子写一篇论文。别问为什么是这个题目，问就是金主爸爸说的。

因为这个文章在最后会被直接使用，这里就把文章的水印功能先关闭。

这个算一个简单的视觉项目，为了UI界面编写的易用性（主要是我就会用ML写）和金主爸爸的要求。

本来按照我平时的路数是要多看几篇好文章动手的，但是时间紧迫，就先一把梭哈了，不看了！

图像处理的话，这个的难点在识别，其实前面的部分叫计算机视觉，后面的部分叫机器视觉，不过很多人也不分。

识别部分主要是传统的方案和现代的神经网络方案，这次选用前者，使用图像的矩特征来分类。

对我而言，视觉就是堆积木，是标准的流程，是共识。

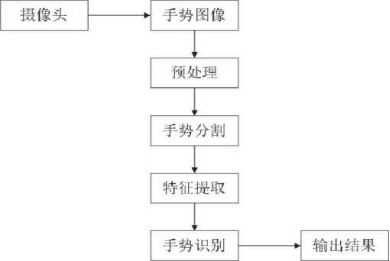
这个是这次大致的项目流程

整个流程就是预处理，中解算，后特征提取和匹配，为了更好的说明算法的有用性，这里也使用了UI的工具，显得更加的牛逼。

直接说干货不太好，说点废话！

人机交互技术也得到了快速发展；人机交5(Human-ComputerInteraction，HCI)是人类与电脑、机器之间的信息交换和交互的技术，是人类和电脑之间的一种桥梁。人类与人之间的互动从世界上首部电脑 ENIAC诞生以来，为了让人类更好地使用电脑，更有效地处理资讯，人类开始寻求更好的方法来进行人机互动。1964年，随着鼠标的产生，出现了图形用户界面(GraphicalUserInterface，GUI)，键盘的诞生又将人机交互的方式推入到字符用户界面时代；随着笔式交互、触摸、语音及基于视频等自然交互设备的出现，人机交互进入了普适计算(PervasiveComputing)时代，自然交互是其研究的重要主题，自然人机交互技术是指能够利用人类自然地认知、感知能力和人类行为习惯的方法。

简而言之，言而总之，这就是个人机交互的好东西~

我们知道论文的前半部分的最后是要给出你研究课题的研究目标的，这个适合使用ChatGPT是最好的！

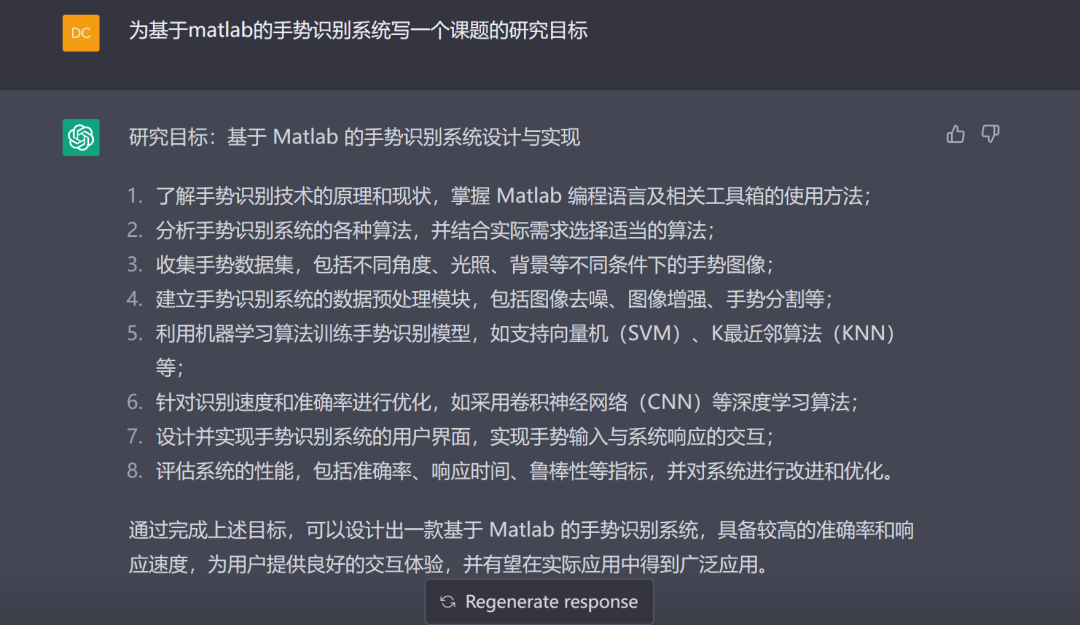
舒服了

但是我们没有使用神经网络算法，所以需要继续调教：

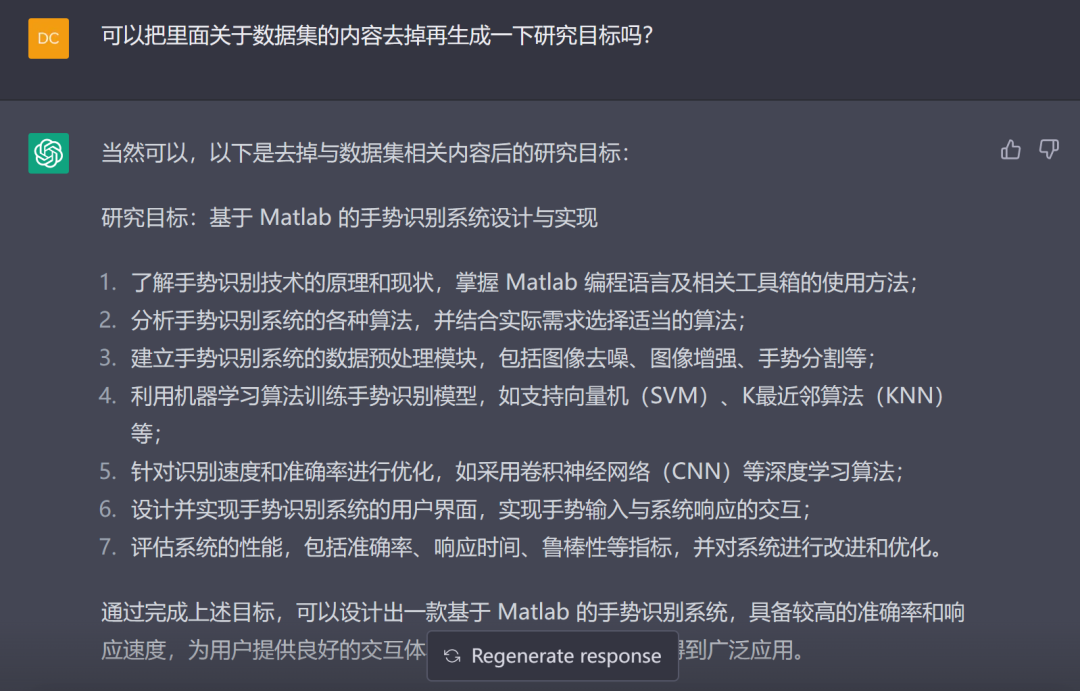
还是可以看到一些关键字

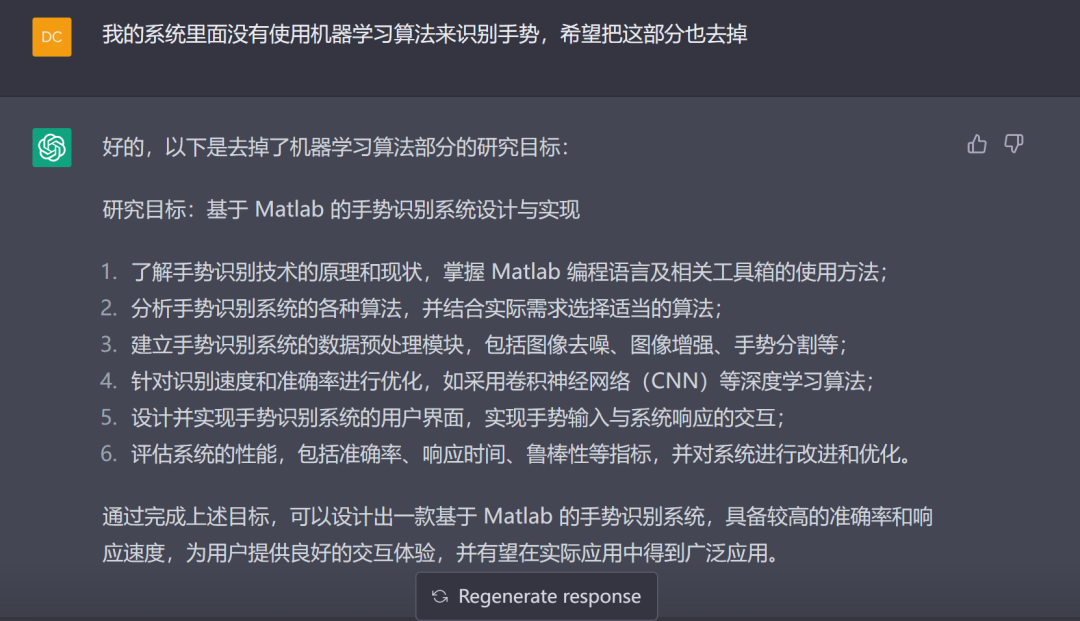
这样就好很多了

但是鄙人有点完美主义，我们重新的来调整：

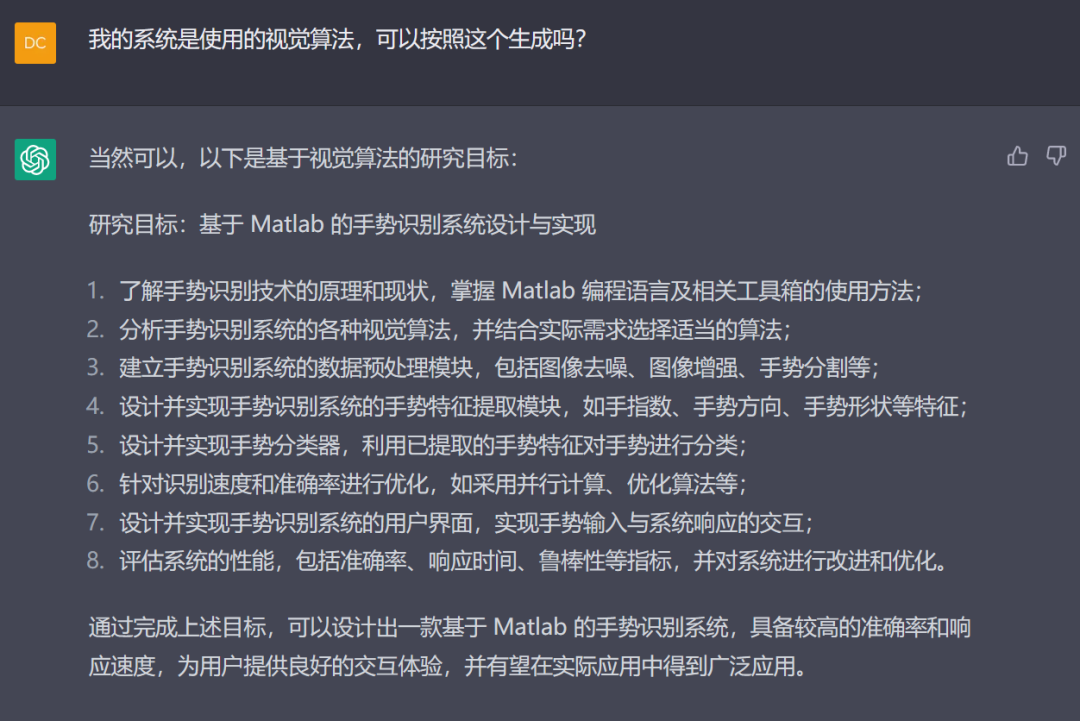
到目前为止，这个就很好了

对大语言模型来说，前面的内容应该尽量的偏大框架，后面的调整先做减法，再做加法。

全程使用的软件就是ML2022A，现在有2023了，对TI的C2000有大支持，其实对我来说也然并卵。

我这里使用的版本是2022

打开ML，设计APP

我以前有个UI的，直接使用但是后面ML的UI工具更新了，这里直接转换

开启这个对齐功能

放大这些边边角角

全部对齐

多用空格按键，平移整个框图

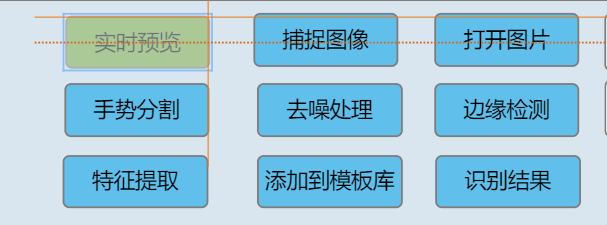
包括按钮也是一样的

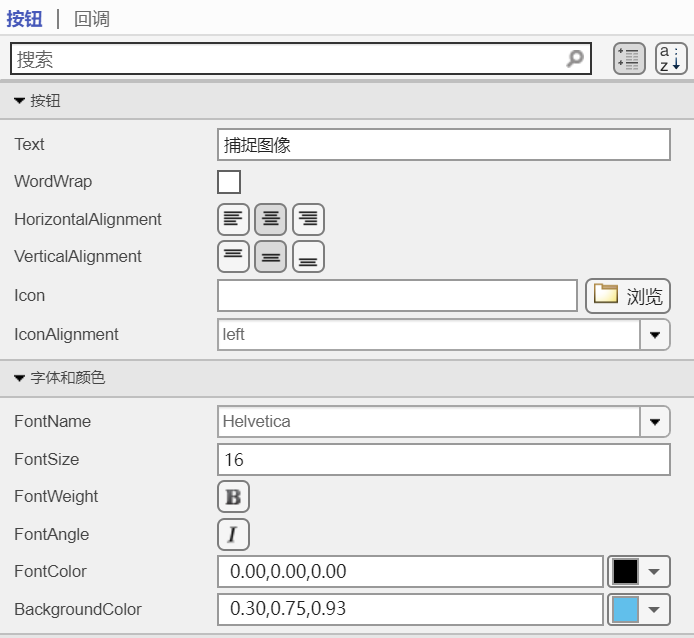
然后这里也会对外观这些可以进行细微的调节

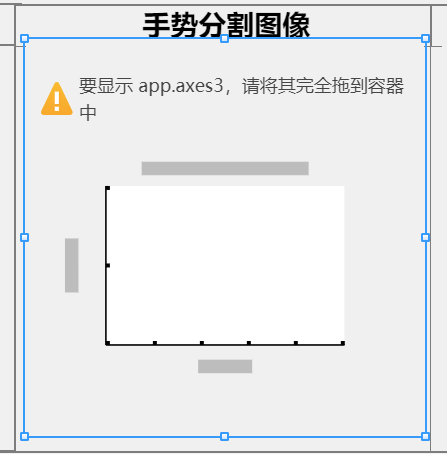
图像显示框要全部搞到容器里面

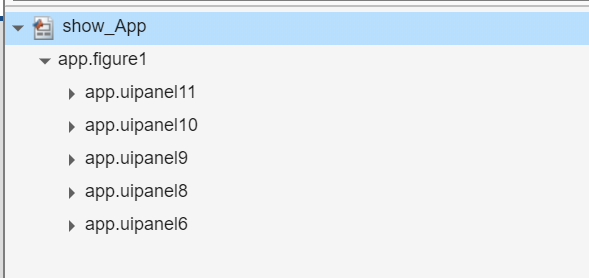
右面是整个的组件树

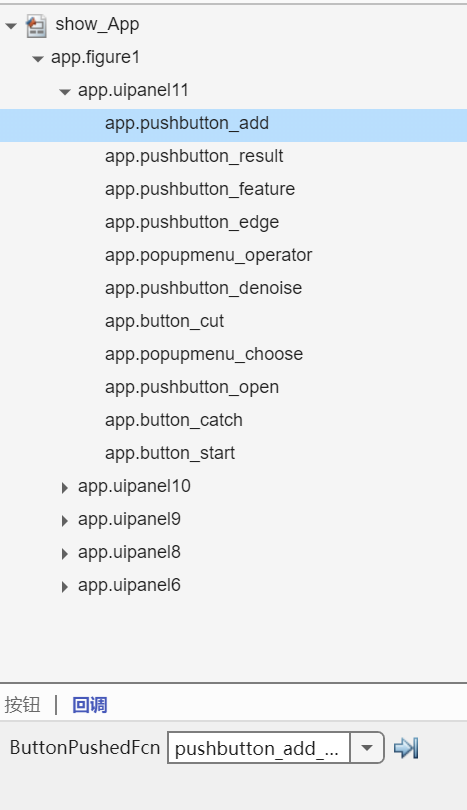
其实在UI系统里面，触发和回调就是全部，触发简单，就是什么事情发生了，接着就是回调，一般意思是把函数当参数传递，但是更加广义的回调应该是有点中断的味道，就是触发了一个实体以后发生了什么，回调本身其实就是发生了什么。

所以按钮和回调进行一个绑定，就是摁下按钮以后会怎么样？

我们的论文基于此，说明了所有的回调函数，就完成了所有的工作。

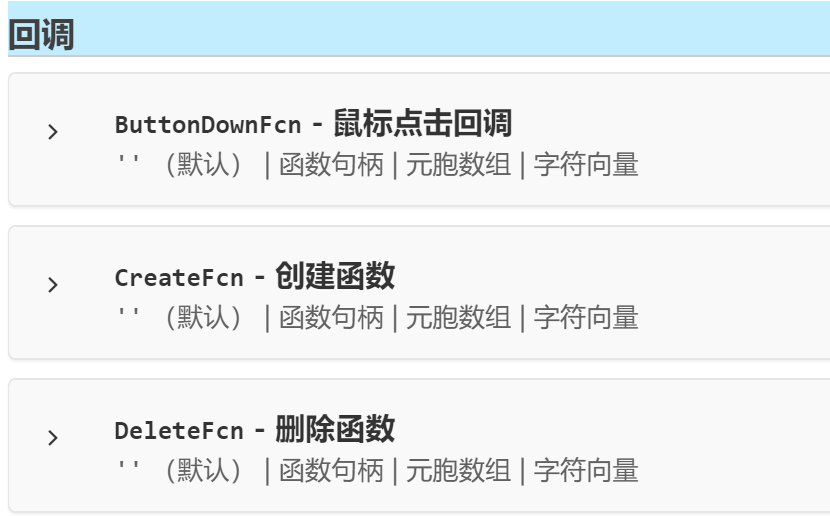
注意要看会响应什么类型的回调

这里就是回调的值

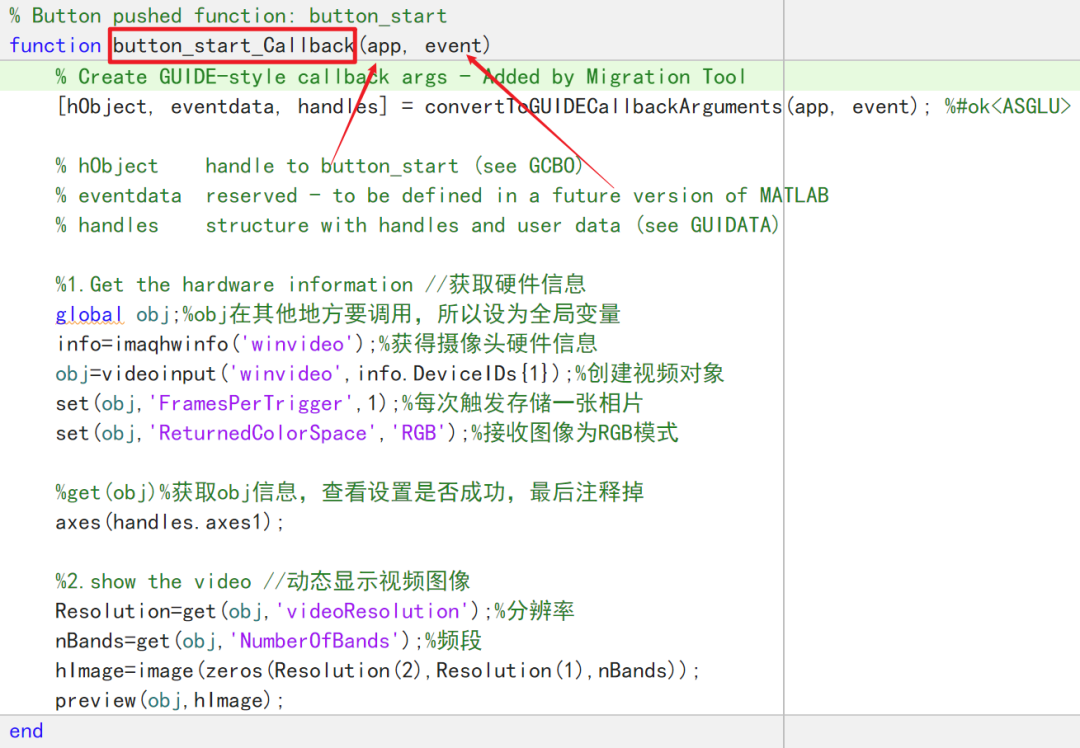
多说无益上代码

这个函数就是实现了最装B的部分，实时的在一个框里面输出视频流。

再看，我们处理的是一帧图像：

可以使用这个函数，获取几帧图像

默认是10，double

然后图像可以使用多种格式储存，我这里设置为RGB，其实YCbCr才好

set(H,Name,Value) 为 H 标识的对象指定其 Name 属性的值。使用时须用单引号将属性名引起来，例如，set(H,'Color','red')。如果 H 是对象的向量，则 set 会为所有对象设置属性。如果 H 为空（即 []），set 不执行任何操作，但不返回错误或警告。

把图像送到坐标区域，就是上面的窗口

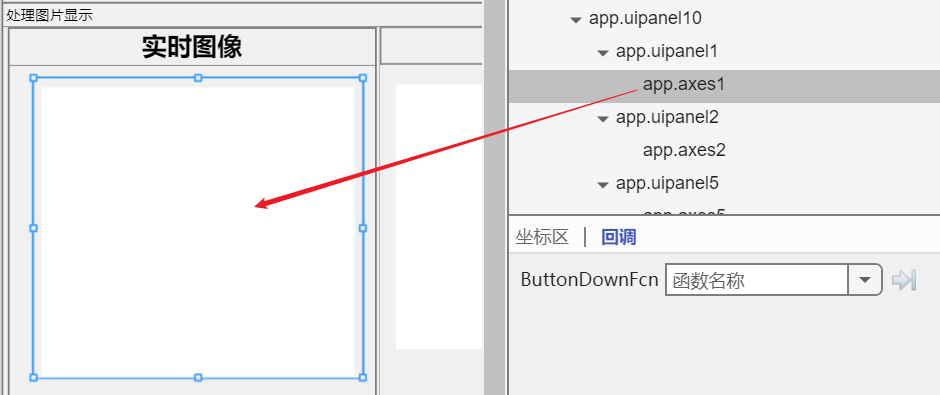
不难吧？    

上面这些操作只是说先显示了一帧而已，接下来是更多的图像。

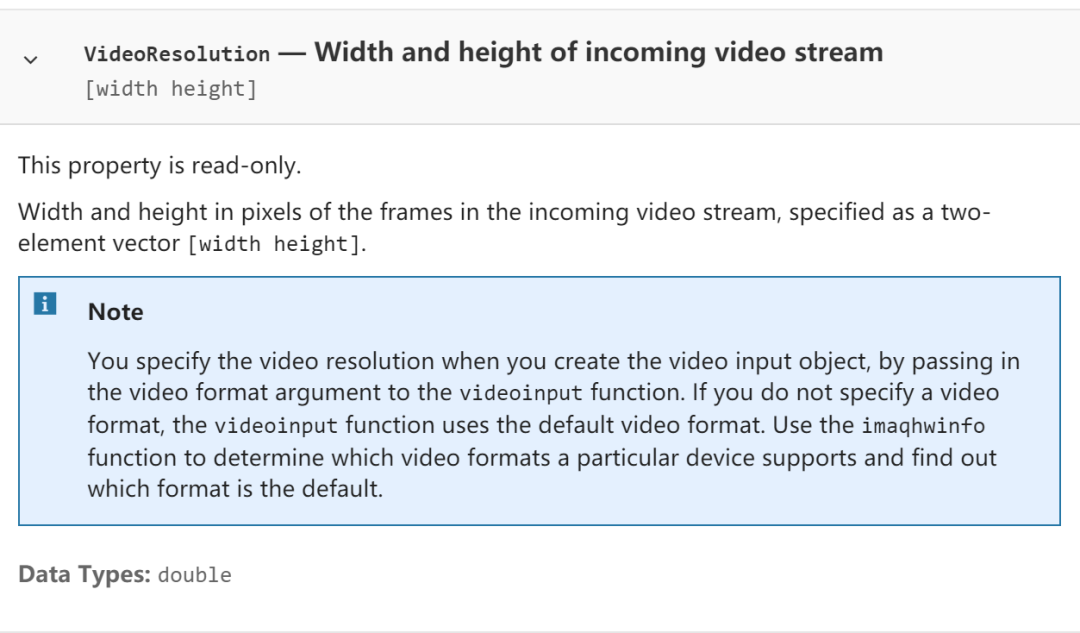
先查询视频流的分辨率

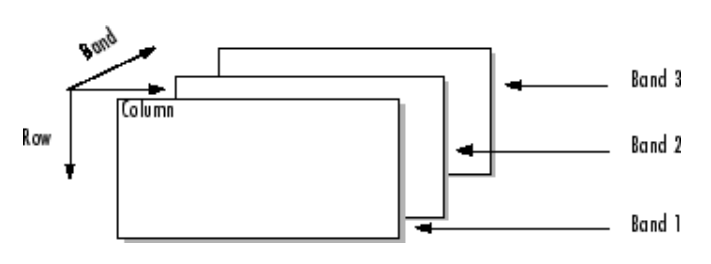
接着要给出颜色的空间

接着按照实际的分辨率来把图像生成

直接显示

其实别觉得难，程序就是关注数据和状态罢了，数据在你手中被重构。

ML的优点就在于帮助文档太好了

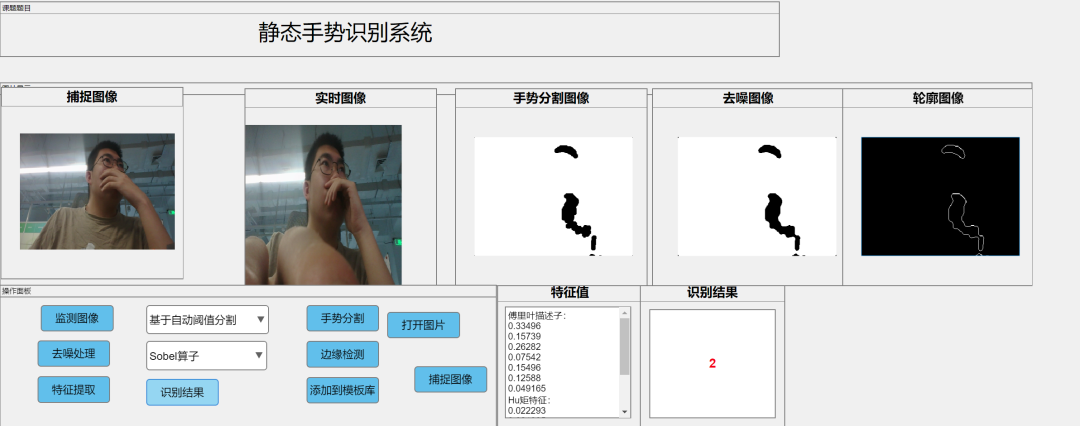
这个是没有修改前

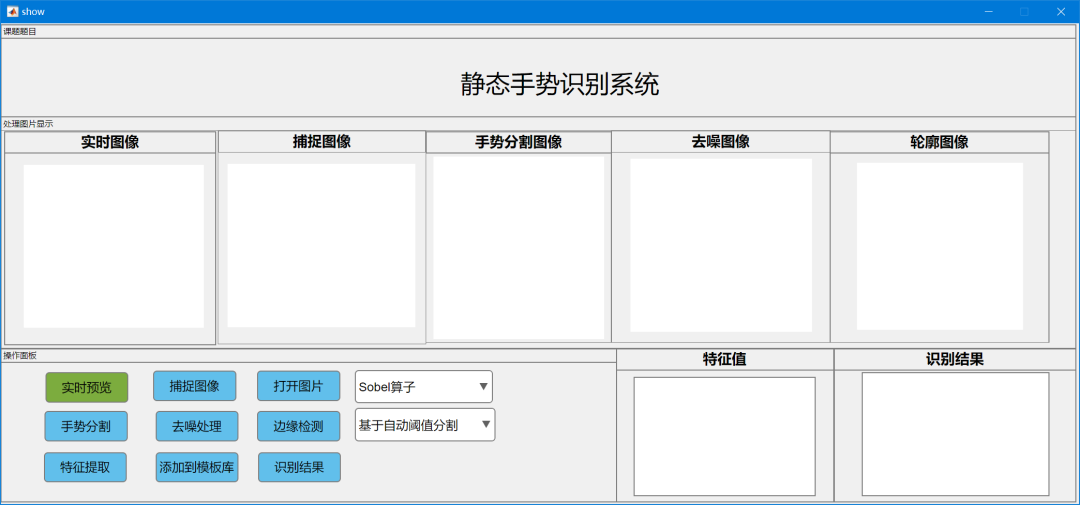
修改后

第二个函数就更简单了，从视频流里面获取一帧

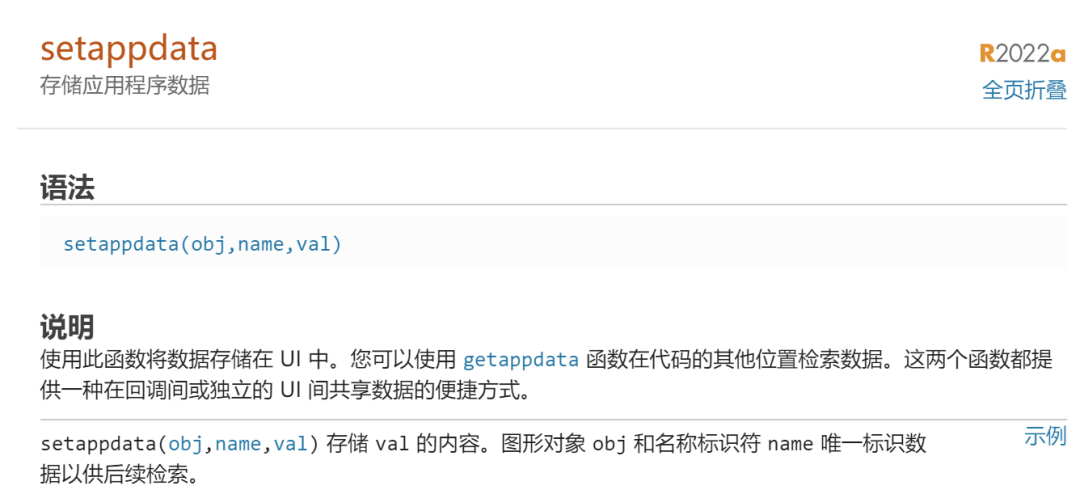
重点看最好一个函数，倒数第二个函数其实已经完成了使命，但是我们后面处理的数据从哪里来？就是这个函数，图像存到pic这个东西里面。

事实上，我还搞了一个可以读取已经有的图片的功能。

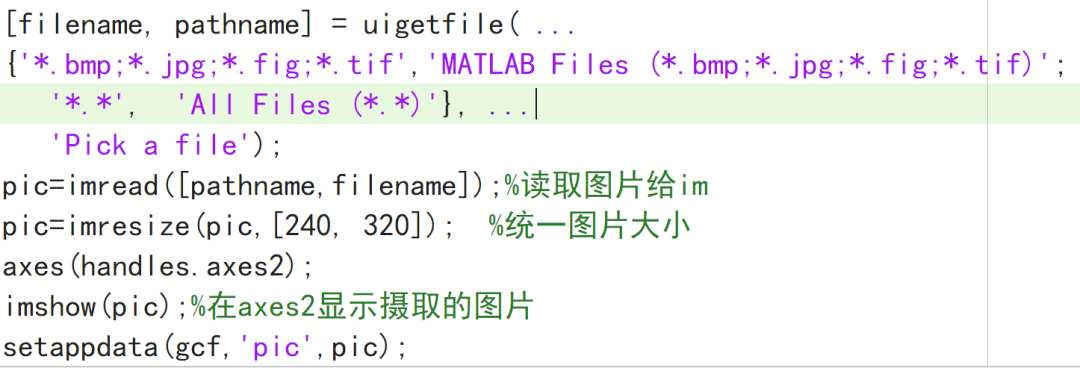
代码也是简单的一笔：

看见了没有，pic就是我们要处理的最终图像，读出来的图像进行缩放，为了提高计算效率，然后在第二个图床上面显示。

接着就是我们要把图像分割出来，事实上我们需要很多的理论知识说明这些，但是好在matlab帮我们都封装好了。

完成一个任务是有不同的算法的选择，我们可以使用下拉框来完成。

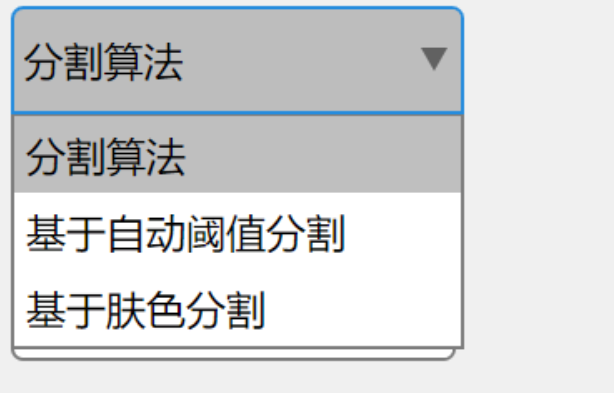
就像这样

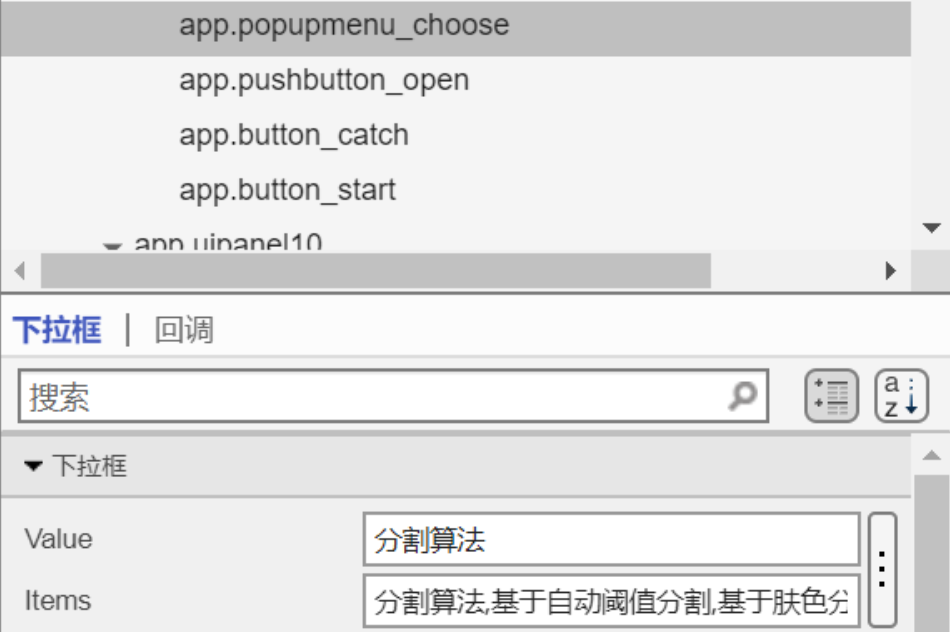
值必须要是下面items里面的

我们使用的就是这个

直接拿到上面传到的图像，下面是取出下来列表的值

如果是阈值分割算法，先转灰度，接着就是局部增强，这个函数不是内置的，需要自己来写：

图像增强（Image Enhancement）其实是一个很宽泛的定义，简单来说就是对数字图像进行调整（adjusting）以使图像更适合于显示或后期的图像分析。

图像增强的原因总结有以下几点：

（1）图像细节不清晰

（2）光照不均匀导致图像亮度分布不均匀

（3）图像对比度较差

（4）成像过程中原始图像受噪声污染

（5）感兴趣区域（Region of Interest）不明显

（6）人眼视觉特性

对于现在有的增强方法是从空间域和变换域说的：

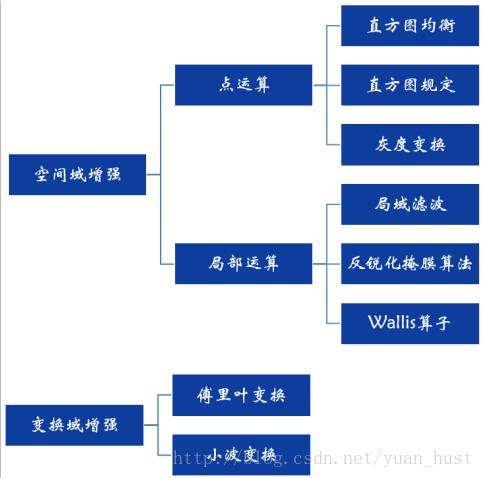
变换方法分类

在图像的小区域细节中，像素数在全局变换的计算中可能被忽略，因为它们没有必要确保局部增强。解决的办法就是在图像中每一个像素的邻域中，根据灰度级分布（或者其他特性）设计变换函数。

以前描述的直方图处理技术很容易适应局部增强，该过程定义一个方形或矩形的邻域并把该区域的中心从一像素移至另一像素。在每个位置的邻域中该点的直方图都要被计算，并且得到的不是直方图均衡化就是规定化变换函数。这个函数最终被用来映射邻域中心像素的灰度。相邻区域的中心然后被移至相邻像素位置并重复这个处理过程。当对某区域进行逐像素转移时，由于只有邻域中新的一行或一列改变，所以可以在每一步移动中，以新数据更新前一个位置获得的直方图。这种方法相比邻域每移动一个像素就对基于所有像素的直方图进行计算，有明显的优点。有时使用非重叠区域是减少计算量的另一种方法。但是这种方法通常会出现不希望的棋盘效果。

分别是源相，全局均衡化，7x7邻域均衡化

这里使用利用直方图统计量来增强局部图像，所以用的原理公式详见冈萨雷斯《数字图像处理》第四版。

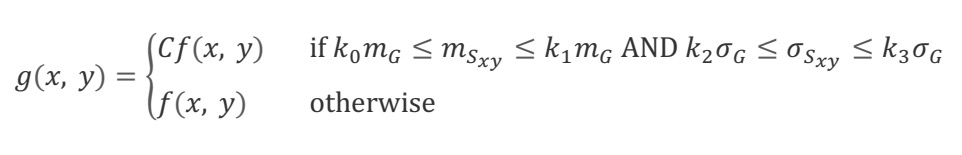
公式的意思是定义一个3x3的领域，平均局部灰度和局部标准差在一定的范围内时，像素乘上C，来增强图像下部分的灰度值，否则就不变。

下面是知乎老哥的，直接梭哈了！

首先我们要将对比度低区域找出来，怎么找呢？我们需要一个比较！我们知道方差体现了一个区域内数值的差距大小，若该区域亮度值相等，则方差为0，而对比度较低区域的方差通常也很小。我们用前面设置的3x3邻域遍历整张图片的每一个像素值，每一次都求一次方差和均值。

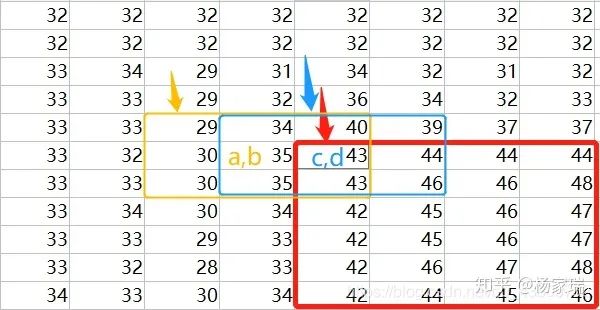
左边对应原图中的白色区域，右图对应原图黑色区域

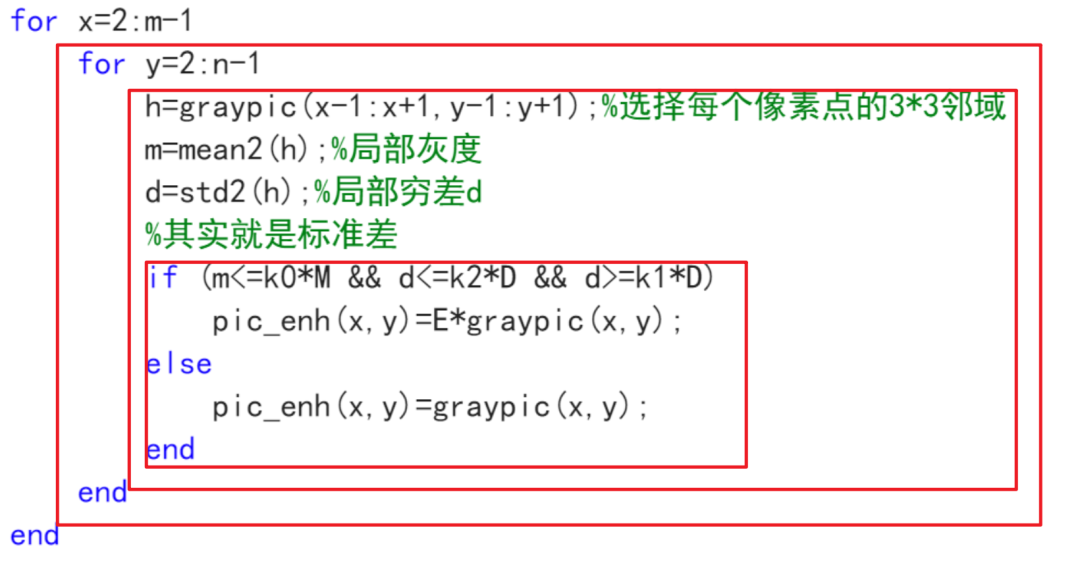
整个判断过程

真实对图像起作用的地方

接着再滤波，其实这里我觉得是没有必要的，因为增强了再滤波信息又没了

不过为了堆算法就再处理一下，如果是搞项目，整个是不可取的，这不二逼行为么、、、

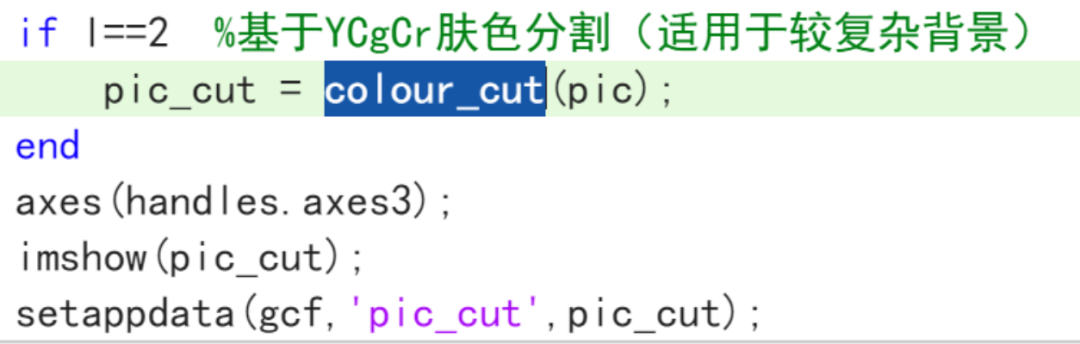
背景复杂的情况下还有肤色分割

平滑滤波是低频增强的空间域滤波技术。它的目的有两类：一类是模糊；另一类是消除噪音。空间域的平滑滤波一般采用简单平均法进行，就是求邻近像元点的平均亮度值。

两个函数搭配起来使用。

色彩空间的转换

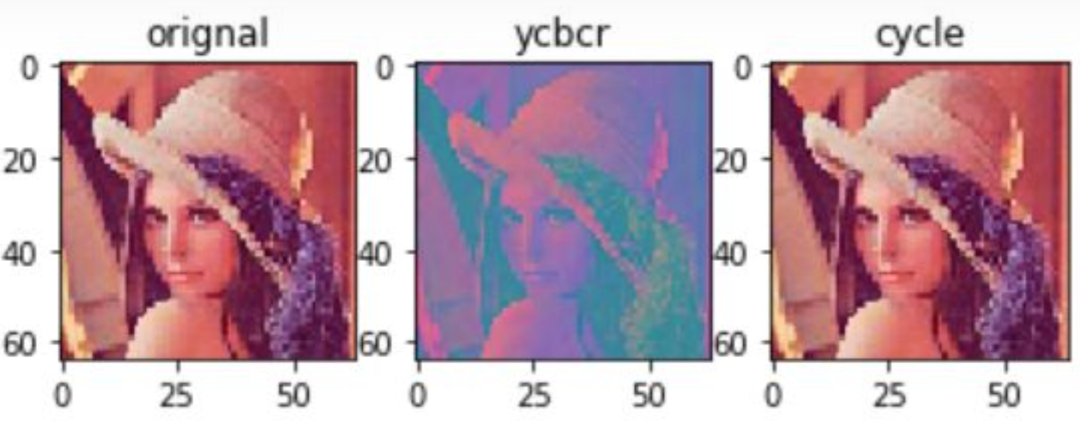
Y=0.257*R+0.564*G+0.098*B+16 Cb=-0.148*R-0.291*G+0.439*B+128 Cr=0.439*R-0.368*G-0.071*B+128

R=1.164*(Y-16)+1.596*(Cr-128) G=1.164*(Y-16)-0.392*(Cb-128)-0.813*(Cr-128) B=1.164*(Y-16)+2.017*(Cb-128)

然后使用find找到index

在颜色里面用集合算区域，然后把区域二值化出来，完成分割。

然后我们看降噪函数

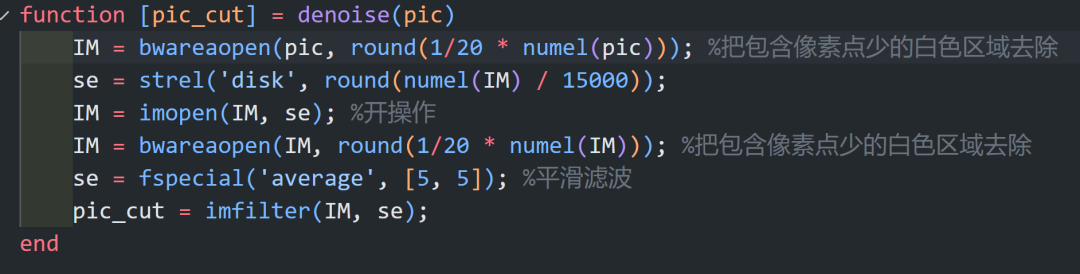
害，ML的编辑器太丑了，我换vscode了

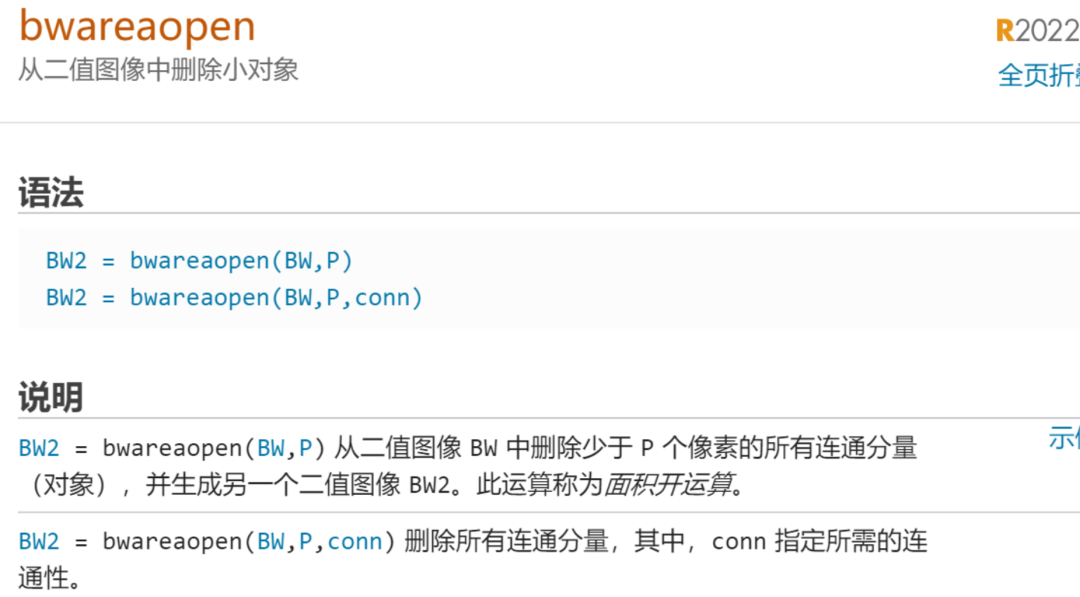
首先我们现在有的图像是一个有一些小窟窿的二值图像，使用这个函数来抠图

给一个要填眼的范围，然后下面就给镶个边

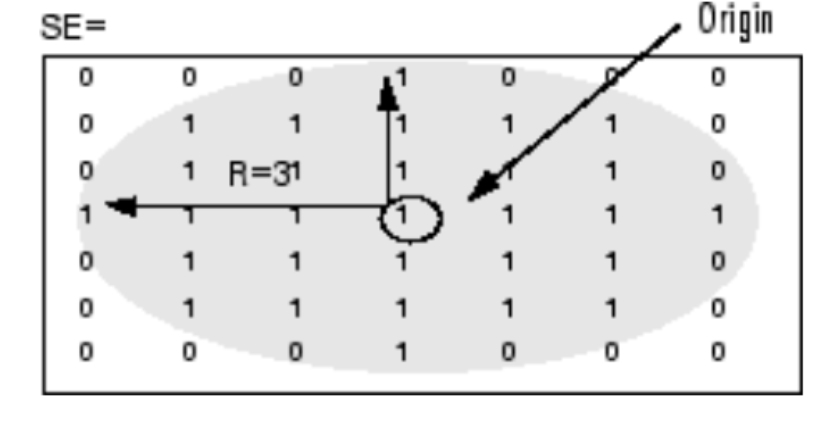
就这

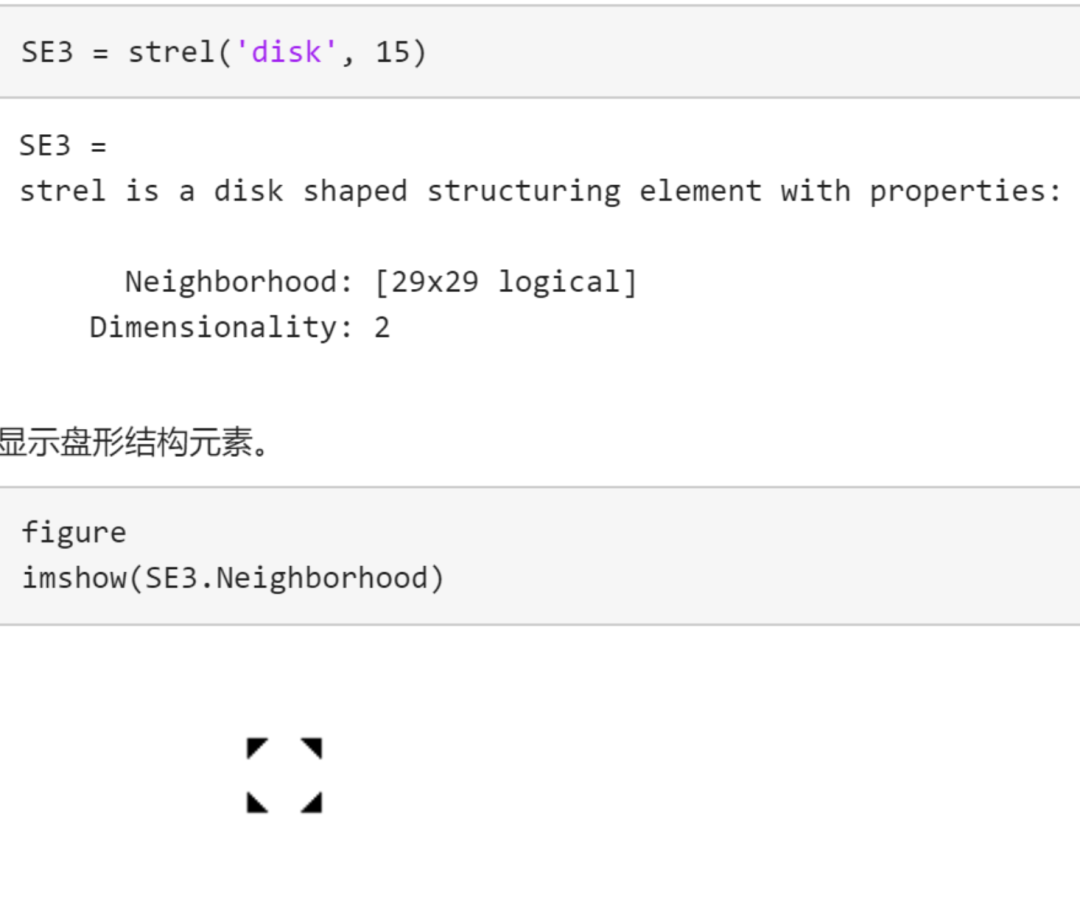
绘制出来就是这样的

执行一下开运算

执行前

执行后

然后再执行上面的操作，最后再滤波一下。

然后就整个降噪也是说完了。

然后说这个获得图像边缘：

一次可以按照上面的写法集成多个算子

来使用Python展示一下这些二值化提取边缘函数的效果：

代码在最后

自带美女

其中，Laplacian算子对噪声比较敏感，由于其算法可能会出现双像素边界，常用来判断边缘像素位于图像的明区或暗区，很少用于边缘检测；Robert算子对陡峭的低噪声图像效果较好，尤其是边缘正负45度较多的图像，但定位准确率较差；Prewitt算子对灰度渐变的图像边缘提取效果较好，而没有考虑相邻点的距离远近对当前像素点的影响；Sobel算子考虑了综合因素，对噪声较多的图像处理效果更好。

自己选吧，我近视眼感觉都差不多。

接着上面的函数继续：

接着我们给它加一个最小的矩形

这太成熟了。。。直接搞现成的代码就好。

这个函数可以求二值图像最小外接矩形（a:面积最小；p：周长最小） 斜矩形

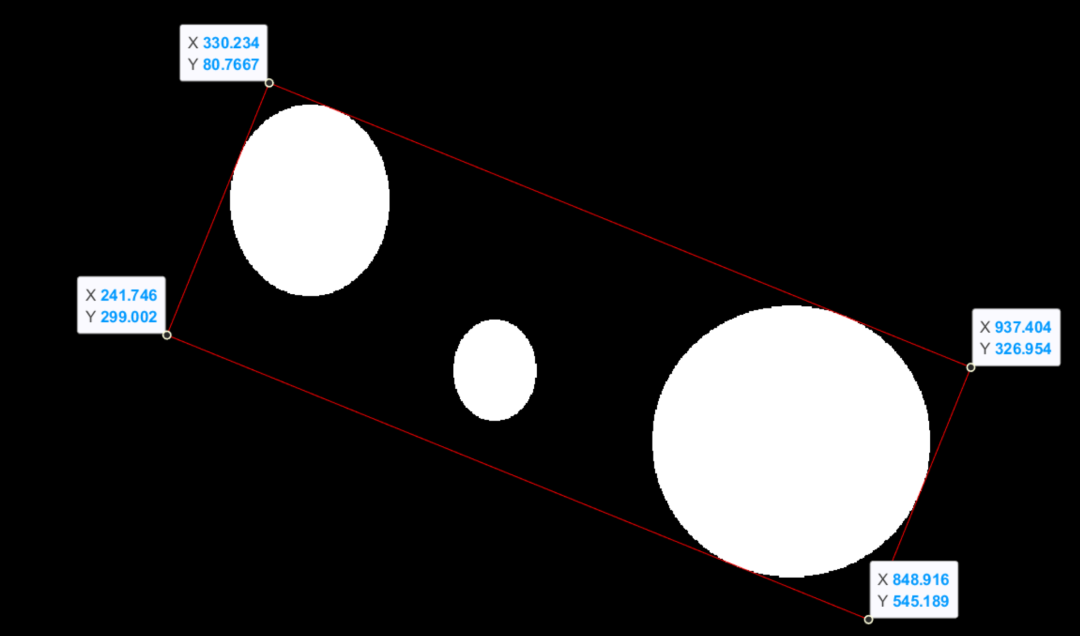
大概的一个效果

除了这个绘制线框以外，还有两个线条

情况就是三个

我们接下来说下一下图像的特征这个事情，无论从前还是现在的神经网络的什么东西，关注的都是图像的特征，这种特征是不随外面的变化而变化的，更多的是哲学上面的性质：

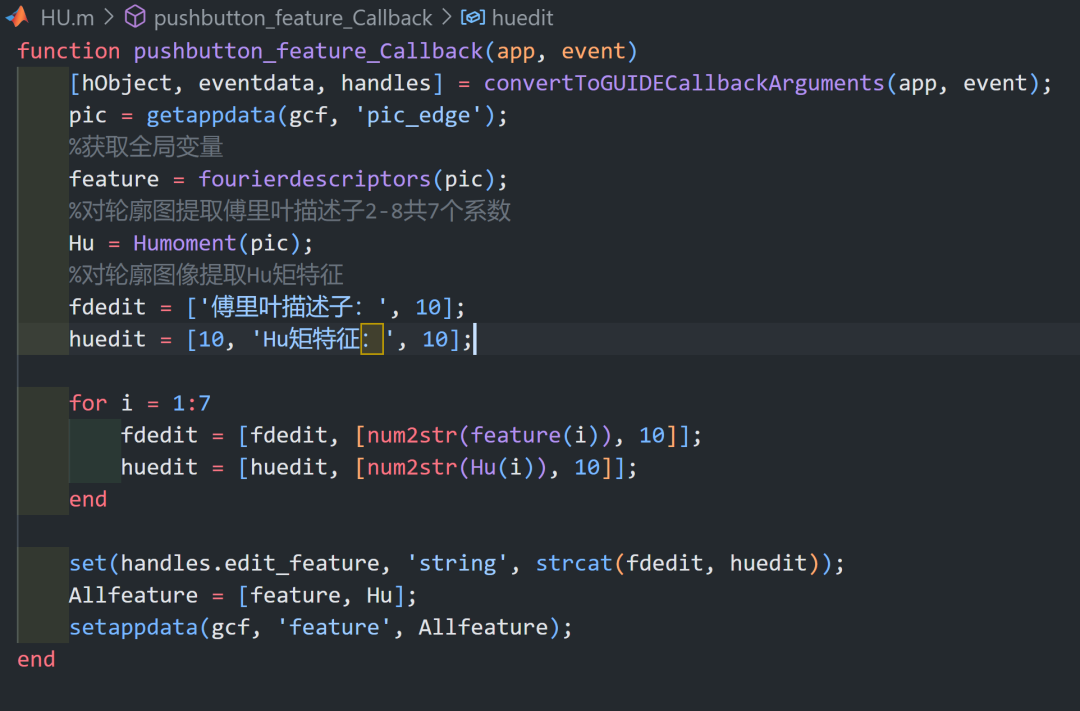
我们用傅里叶描述子和Hu矩来说明这个

傅里叶描述子是一种图像特征，具体来说，是一个用来描述轮廓的特征参数。其基本思想是用物体边界信息的傅里叶变换作为形状特征，将轮廓特征从空间域变换到频域内,，提取频域信息作为图像的特征向量。即用一个向量代表一个轮廓，将轮廓数字化，从而能更好地区分不同的轮廓，进而达到识别物体的目的。

冈萨雷斯的《数字图象处理》

总结：傅立叶描述子可以很好地描述轮廓特征，并且只需少量的描述子（即向量中的数不需要太多）即可大致代表整个轮廓。其次，对傅立叶描述字进行简单的归一化操作后，即可使描述子具有平移、旋转、尺度不变性，即不受轮廓在图像中的位置、角度及轮廓的缩放等影响，是一个鲁棒性较好的图像特征。

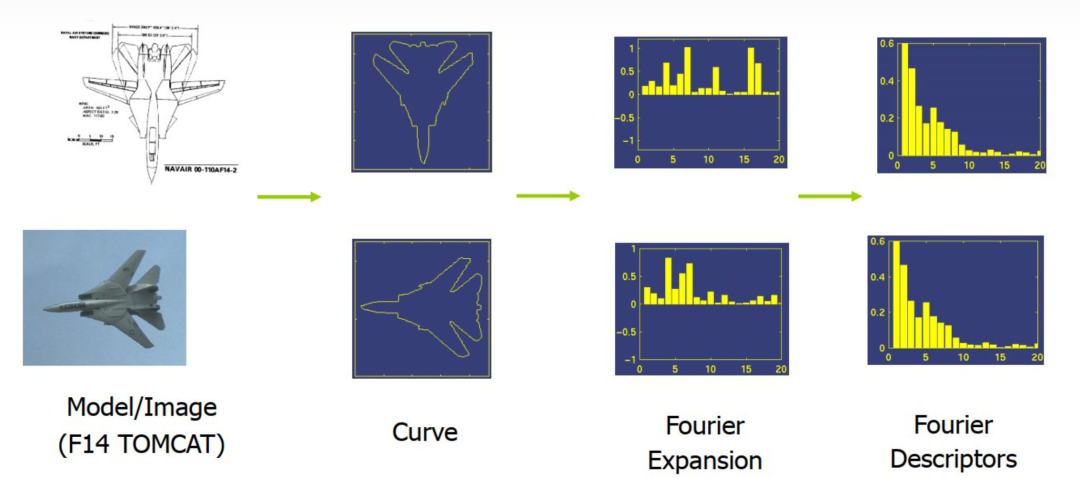
看最后图的两个的样子

比较两个轮廓最简单的方法是比较二者的轮廓矩，轮廓矩代表了一个轮廓，一副图像，一组点集的全局特征，矩信息包含了对应对象不同类型的集合特征，例如大小，位置，角度，形状等。

Hu矩是归一化中心矩的线性组合，Hu矩再图像旋转，缩放，平移等操作后，仍能保持矩的不变性，经常使用 Hu 矩来识别图像的特征。

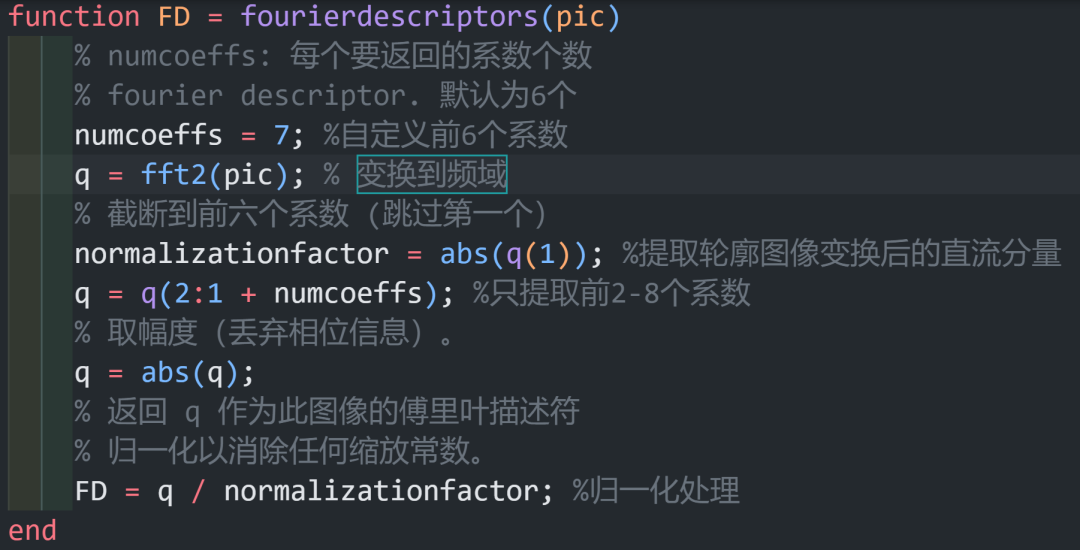
我们要单独的构建一个函数

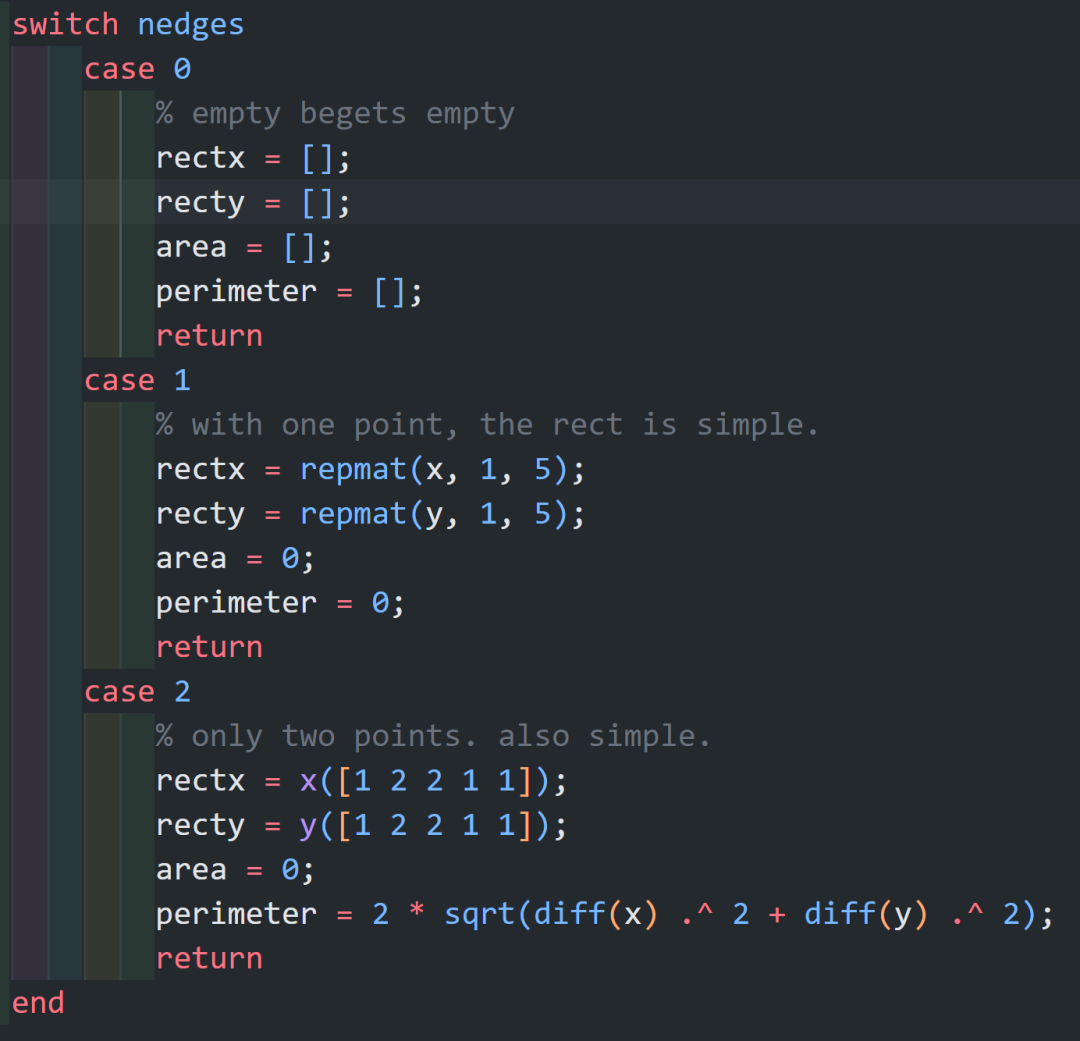
等下再说这个，我们再贴一下Hu的实现：

5，6，7后面还有很长的公式就不放了

直接使用现成的函数来求解

使用的函数是这个

别问太多的原理，我研究透了肯定会写，现在能快速实现最重要，毕竟我快饿死了。

矩是一个数学的概念

根据矩的定义，二维图像的灰度用f(x,y)表示，零阶矩m00表示为：

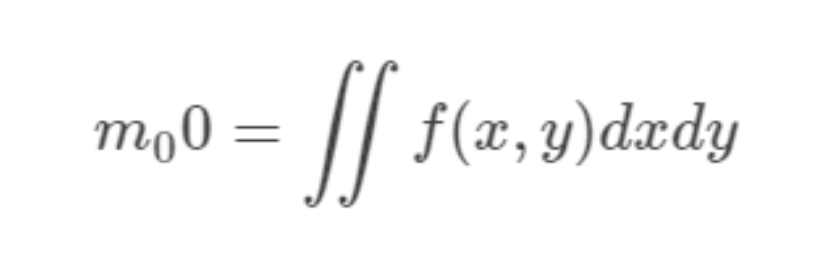
表示的是图像灰度的总和

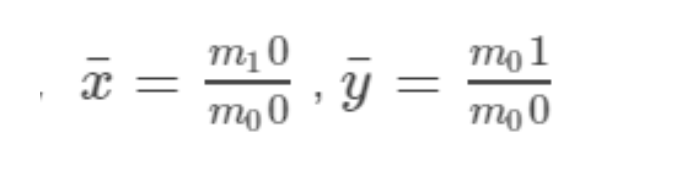
根据中心矩的定义很容易计算出，u10=0,u01=0

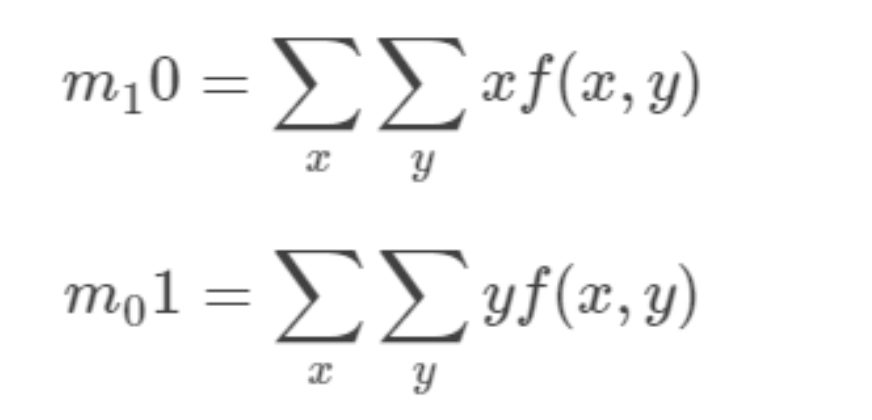
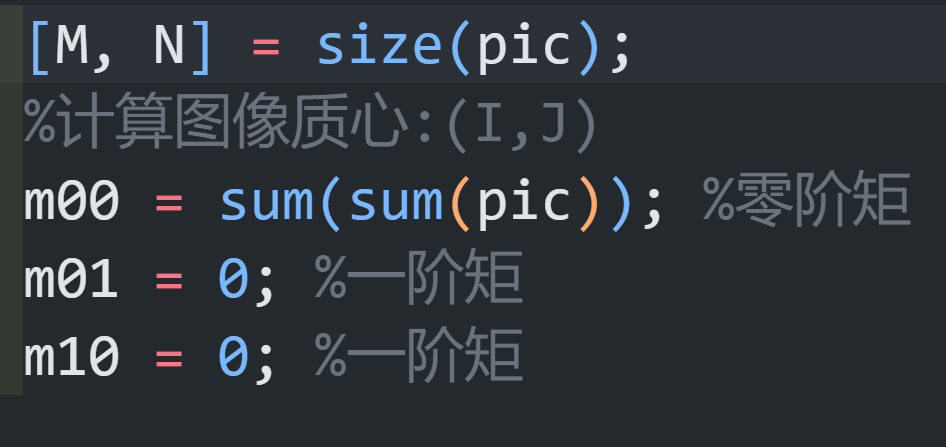
算球算，直接写

二阶矩有三个，m11 m02 m20，也成为惯性矩。它们可以确定物体的几个特性： 

1.二阶中心矩用来确定目标物体的主轴，长轴和短轴分别对应最大和最小的二阶中心矩。可以计算主轴方向角。 

2.图像椭圆：由一阶、二阶矩可以确定一个与原图像惯性等价的图像椭圆。所谓图像椭圆是一个与原图像的二阶矩及原图像的灰度总和均相等的均匀椭圆。使得主轴与图像的主轴方向重合，一边分析图像性质。

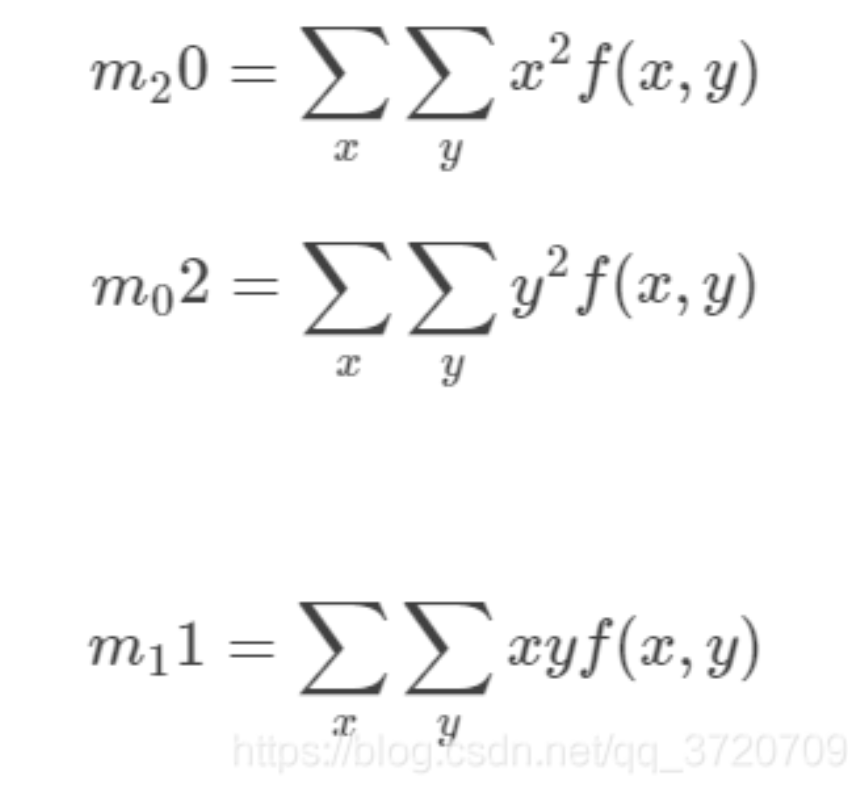
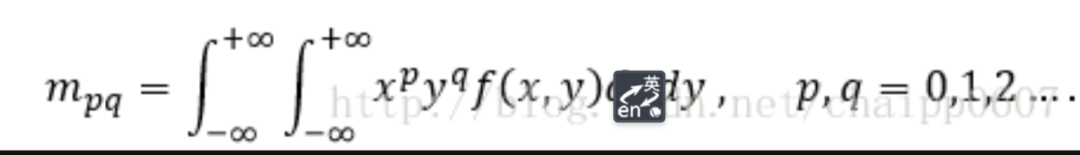
而数字图像是一个二维的离散信号，对上述公式进行离散化之后：

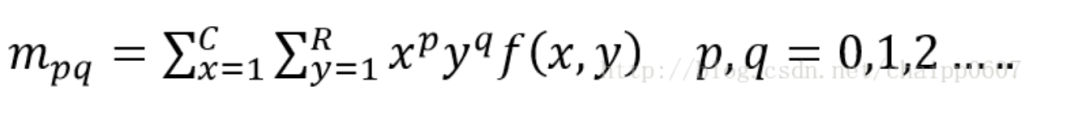
C，R，行列

各种矩的物理意思：

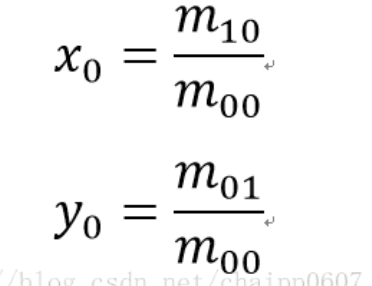
由求得的质心坐标，我们可以构造出中心矩：

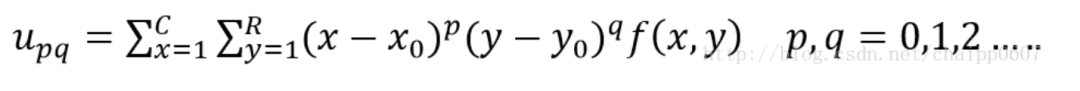
由于我们选择了以目标区域的质心为中心构建中心矩，那么矩的计算时永远是目标区域中的点相对于目标区域的质心，而与目标区域的位置无关，及具备了平移不变性。

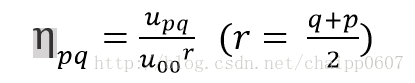
Hu矩：构造旋转不变性 
利用二阶和三阶规格中心矩可以导出下面7个不变矩组(Φ1 Φ7)，它们在图像平移、旋转和比例变化时保持不变。 

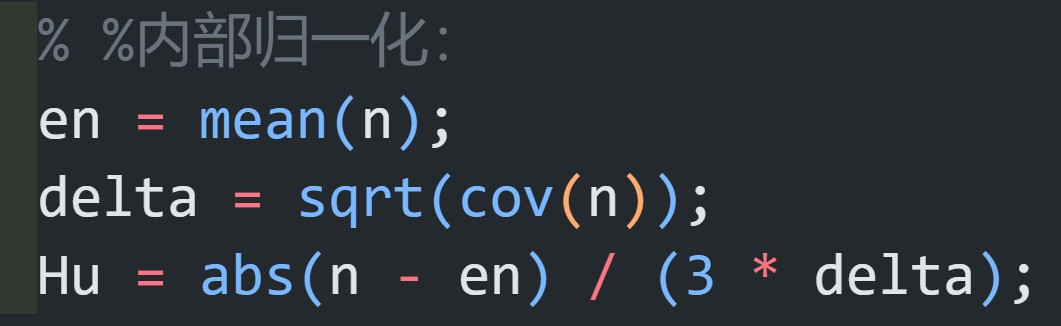
按照分析记得代码的归一化

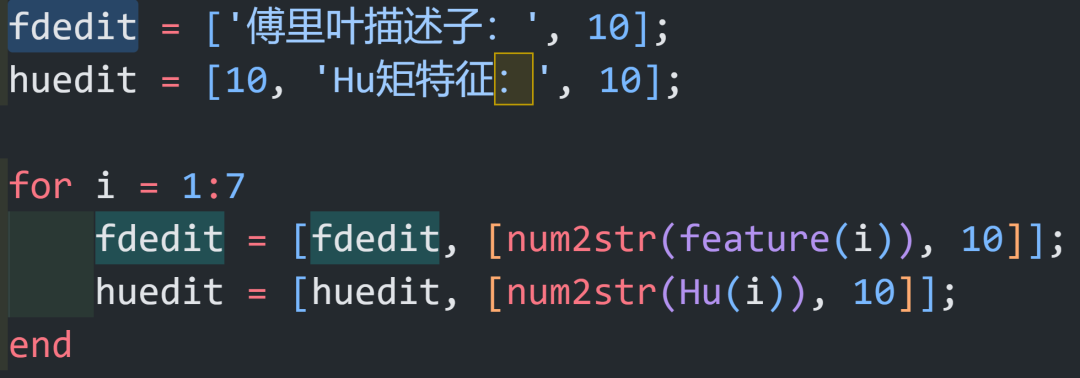
然后把特征值写到数组里面

通过找到上面的区域，显示上去

最后一步了，查找特征值有没有，如果没有就msgbox弹出

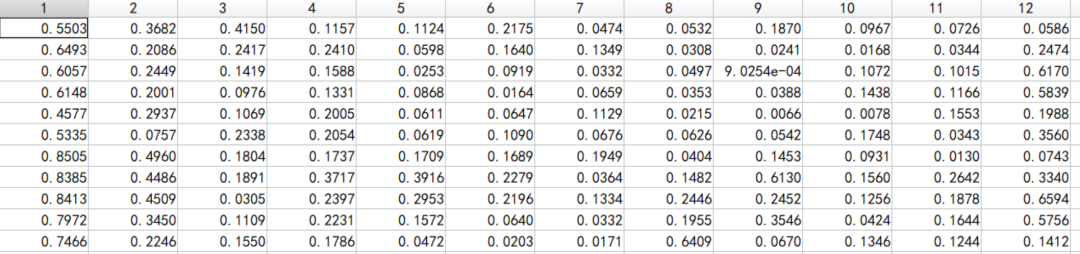
data文件是提前算好的数据

算好的，已有的，这明显就是一个距离的问题：

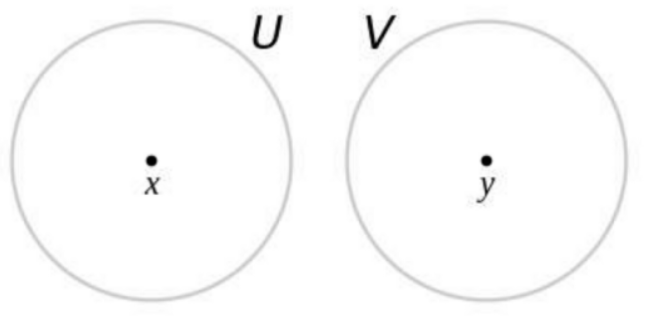
我们使用豪斯多夫距离

代码在最后

循环的从中取出距离来对比就给出了结果

至于代码，不准备开源，有需要的来买。

https://blog.csdn.net/weixin_46118768/article/details/119866798

function [mhd] = ModHausdorffDist(A, B)    Asize = size(A);    Bsize = size(B);
    % Check if the points have the same dimensions    if Asize(2) ~= Bsize(2)        msgbox('两个集合的维数不同，请统一！', '提示');    else        % Calculating the forward HD        fhd = 0; % Initialize forward distance to 0
        for a = 1:Asize(1) % Travel the set A to find avg of d(A,B)            mindist = Inf; % Initialize minimum distance to Inf
            for b = 1:Bsize(1) % Travel set B to find the min(d(a,B))                tempdist = norm(A(a, :) - B(b, :));
                if tempdist < mindist                    mindist = tempdist;                end
            end
            fhd = fhd + mindist; % Sum the forward distances        end
        fhd = fhd / Asize(1); % Divide by the total no to get average        % Calculating the reverse HD        rhd = 0; % Initialize reverse distance to 0
        for b = 1:Bsize(1) % Travel the set B to find avg of d(B,A)            mindist = Inf; % Initialize minimum distance to Inf
            for a = 1:Asize(1) % Travel set A to find the min(d(b,A))                tempdist = norm(A(a, :) - B(b, :));
                if tempdist < mindist                    mindist = tempdist;                end
            end
            rhd = rhd + mindist; % Sum the reverse distances        end
        rhd = rhd / Bsize(1); % Divide by the total no. to get average        mhd = max(fhd, rhd); % Find the minimum of fhd/rhd as        % the mod hausdorff dist    end
end

原文链接：https://blog.csdn.net/devcloud/article/details/126764789

# -*- coding: utf-8 -*-import cv2import numpy as npimport matplotlib.pyplot as plt
# 读取图像grayImage = cv2.imread('./222.png', cv2.IMREAD_GRAYSCALE)
# 高斯滤波gaussianBlur = cv2.GaussianBlur(grayImage, (3, 3), 0)
# 阈值处理ret, binary = cv2.threshold(gaussianBlur, 68, 255, 0)
# Roberts算子kernelx = np.array([[-1, 0], [0, 1]], dtype=int)kernely = np.array([[0, -1], [1, 0]], dtype=int)x = cv2.filter2D(binary, cv2.CV_16S, kernelx)y = cv2.filter2D(binary, cv2.CV_16S, kernely)absX = cv2.convertScaleAbs(x)absY = cv2.convertScaleAbs(y)Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
# Prewitt算子kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int)kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int)x = cv2.filter2D(binary, cv2.CV_16S, kernelx)y = cv2.filter2D(binary, cv2.CV_16S, kernely)absX = cv2.convertScaleAbs(x)absY = cv2.convertScaleAbs(y)Prewitt = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
# Sobel算子x = cv2.Sobel(binary, cv2.CV_16S, 1, 0)y = cv2.Sobel(binary, cv2.CV_16S, 0, 1)absX = cv2.convertScaleAbs(x)absY = cv2.convertScaleAbs(y)Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
# Laplacian算子dst = cv2.Laplacian(binary, cv2.CV_16S, ksize=3)Laplacian = cv2.convertScaleAbs(dst)

# 用来正常显示中文标签plt.rcParams['font.sans-serif'] = ['SimHei']
# # 显示图形plt.figure(figsize=(12, 5))plt.subplot(231), plt.imshow(grayImage), plt.title(    '原始图像'), plt.axis('off')  # 坐标轴关闭plt.subplot(232), plt.imshow(    binary, cmap=plt.cm.gray), plt.title('二值图'), plt.axis('off')plt.subplot(233), plt.imshow(Roberts, cmap=plt.cm.gray), plt.title(    'Roberts算子'), plt.axis('off')plt.subplot(234), plt.imshow(Prewitt, cmap=plt.cm.gray), plt.title(    'Prewitt算子'), plt.axis('off')plt.subplot(235), plt.imshow(Sobel, cmap=plt.cm.gray), plt.title(    'Sobel算子'), plt.axis('off')plt.subplot(236), plt.imshow(Laplacian, cmap=plt.cm.gray), plt.title(    'Laplacian算子'), plt.axis('off')
plt.show()

https://blog.csdn.net/sml115161/article/details/120689698

https://ww2.mathworks.cn/help/releases/R2020b/images/ref/imfilter.html

https://blog.csdn.net/qq_43826220/article/details/127568505