--关注回复“26262”--
↓↓领取:ISO 26262↓↓
通常来说,并道无论对于自动驾驶还是有人驾驶都是挑战性的任务,尤其是在密集的交通流场景中,因为并道的车辆通常需要与他车交互,以识别或创造出空间,实现安全并入。本文研究了强制并道场景下自动驾驶车辆的控制问题。我们提出了一种新的基于博弈的控制器,称为领导者-跟随者博弈控制器(LFGC)。其中,使用了部分可观的领导者-跟随者博弈模型建模自动驾驶车辆与其他具有先验不确定驾驶意图的车辆之间的交互行为。LFGC根据观察到的轨迹在线估计他车的意图,预测它们未来的轨迹,并使用模型预测控制(MPC)规划自车辆轨迹,以在实现并入目标的同时保证安全概率。为了验证LFGC的性能,我们使用仿真及NGSIM数据对其进行了测试,其中LFGC展示了高达97.5%的并入成功率。高度自动驾驶汽车的实现仍然面临很多挑战[4],公路上完成强制并道对于有人驾驶和自动驾驶来说都是具有挑战性的场景。强制并道通常指当前车道结束、需要强制并道的场景,例如高速公路入口匝道并入。交通密集时,并道车辆与目标车道行驶的车辆交互和/或合作。此时,目标车道上的车辆可以选择忽略并道车辆(即继续行驶),此时并入车辆只能在其后并道;或者,目标车道中的车辆可以选择屈服于并道(即让并入车辆并道至其前方)。为了成功地并入密集交通流,自动驾驶车辆控制器需要对目标车道车辆的继续或屈服的意图合理预测,以做出合适地响应。同时,他车的意图不仅取决于交通状况(如两辆车之间的相对位置和速度),还取决于驾驶员的普遍具有的驾驶风格、个性、情绪等。比如激进的司机可能倾向于继续行驶,而谨慎、保守的司机可能倾向于屈服。这对自动驾驶汽车的规划和控制提出了重大挑战。当前很多学者使用部分可观察马尔可夫决策过程(POMDP)框架处理交互的不确定性(例如,由于他车的不同合作意图),然而,该方法对计算的要求高[11],难以用于多车辆交互。强化学习(RL)方法是另一种针对变道或并道场景设置控制策略[12][13]的流行方法。基于RL的方法具备处理复杂的交通下多车交互场景的能力,但RL缺乏可解释性和明确的安全保证。为了实现更可解释的控制,有研究人员提出在控制算法中显示加入车辆交互的预测模型。如[22]使用 “社会生成对抗网络(GAN)”来预测他车的未来轨迹,以响应自车的行为。然而,SocialGAN未考虑到司机的风格和意图的变化,需要用巨大的交通数据[23]进行训练;有的研究中使用博弈论方法建模变道或并道场景[9]、[25]、[26]、[27]、[28]、[29]下的车辆交互,可以解释不同的驾驶风格和/或意图,如通过博弈建模和在线估计驾驶员的认知水平[26]或攻击性[30],[31]。在本文提出了一种新的高级控制算法,称为领导者-跟随者博弈控制器(LFGC),用于强制并道场景下的自动驾驶车辆的规划和控制。在LFGC中,使用显式博弈论建模驾驶员的交互意图(继续或屈服)以及由此产生的车辆行为。因为模型具有多个并行领导者-跟随者对,故称为领导者-跟随者博弈[32]。考虑交互的不确定性,将两车辆间先验不确定的领导者-跟随者关系建模为潜在变量。LFGC根据观察到的轨迹在线估计领导者-跟随者关系,并使用基于模型预测控制(MPC)的策略为自主自车做出最优决策。因此,所提出的LFGC适应于评估预测领导-跟随者关系,以在实现并道的同时保证概率安全。1)使用LFGC博弈模型进行车辆轨迹预测,同时考虑他车交互和合作意图,接入MPC控制后产生可解释的控制方案。2)LFGC通过将不确定性建模为潜在变量,基于历史观察轨迹集合贝叶斯推理在线估计,以处理由于他车的不同合作意图造成的交互不确定性。3)LFGC建立车辆安全要求(如避免碰撞)的约束条件,在满足明确的概率安全特征(即用户指定的安全概率边界内)的情况下进行优化。4)LFGC是在连续状态空间设置下设计,降低离散空间的计算成本,能够处理更复杂的多车交互场景。5) LFGC的可行性通过了基于模拟的全面的案例验证,包括他车由各种类型的驾驶员模型控制的案例,以及在NGSIM美国高速公路101数据集[34]中的实际案例。并在实际案例仿真中显示了高达97.5%的成功率。本节中基于表示车辆和交通动力学的模型,建立了基于MPC的自车轨迹规划策略。在我们使用运动学自行车模型[35]中,自行车模型的连续时间方程如下,假设只有前轮转向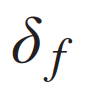 ,没有后轮转向(即
,没有后轮转向(即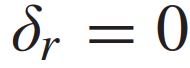 );x、y是车辆的纵向、横向位置;v是车辆的速度;ψ和β是车辆的偏航角和滑移角;
);x、y是车辆的纵向、横向位置;v是车辆的速度;ψ和β是车辆的偏航角和滑移角;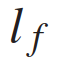 和
和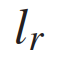 表示车辆从CG到前轮和后轮轴的距离;a是沿速度v方向的加速度。控制输入是加速和前轮转向,
表示车辆从CG到前轮和后轮轴的距离;a是沿速度v方向的加速度。控制输入是加速和前轮转向,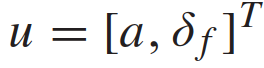 。场景包括用1个自车和n个他车,交通状态及其动力学的特征是所有n+1车辆的状态和动力学的聚集。具体使用以下离散时间模型来描述交通动态:其中,
。场景包括用1个自车和n个他车,交通状态及其动力学的特征是所有n+1车辆的状态和动力学的聚集。具体使用以下离散时间模型来描述交通动态:其中,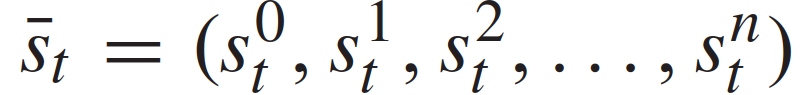 表示离散时刻的n+1量车的交通状态,
表示离散时刻的n+1量车的交通状态,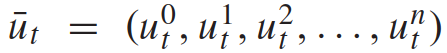 表示时间t时所有n + 1辆车辆的控制输入的集合。每辆车的状态
表示时间t时所有n + 1辆车辆的控制输入的集合。每辆车的状态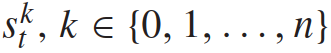 包括它的xy坐标、速度和偏航角;控制输入
包括它的xy坐标、速度和偏航角;控制输入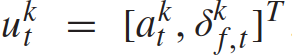 。奖励函数
。奖励函数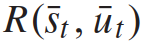 是驾驶员驾驶目标的数学表示,交通状态是由这两辆车的状态组成的,而自车获得的奖励取决于两交互车的状态和控制输入。我们考虑其中,
是驾驶员驾驶目标的数学表示,交通状态是由这两辆车的状态组成的,而自车获得的奖励取决于两交互车的状态和控制输入。我们考虑其中,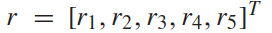 ,
,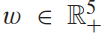 是一个权重向量。奖励项
是一个权重向量。奖励项 代表驾驶过程中的以下常见考虑:1)安全性
代表驾驶过程中的以下常见考虑:1)安全性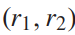 ,即不与他车相撞、不离开道路;2)并道意愿
,即不与他车相撞、不离开道路;2)并道意愿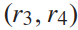 ,即与目的车道的距离;3)舒适性
,即与目的车道的距离;3)舒适性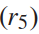 ,即与他车保持合理的间距。
,即与他车保持合理的间距。 的更定义详见[33]。我们考虑
的更定义详见[33]。我们考虑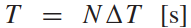 上的车辆运动轨迹样本作为每个车辆的动作空间。具体来说,每个轨迹都是从车辆当前状态
上的车辆运动轨迹样本作为每个车辆的动作空间。具体来说,每个轨迹都是从车辆当前状态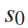 开始的车辆状态
开始的车辆状态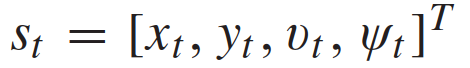 的时间历史。根据车辆动力学模型(1),可以将每个轨迹对应的控制输入时间历史
的时间历史。根据车辆动力学模型(1),可以将每个轨迹对应的控制输入时间历史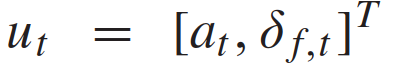 计算出来。对于在目标车道上行驶的交互车辆,我们只考虑它们的纵向运动。假设
计算出来。对于在目标车道上行驶的交互车辆,我们只考虑它们的纵向运动。假设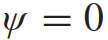 和
和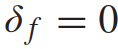 ,这些车辆的运动学模型(1)简化为:此时从给定的初始条件开始的轨迹只依赖于[0,T]的加速度a。在每个样本时间都会考虑81个加速度曲线,即81个满足表达式(4)的轨迹,由此形成在目标车道上驾驶的他车的轨迹可行域。这81个轨迹符合速度约束
,这些车辆的运动学模型(1)简化为:此时从给定的初始条件开始的轨迹只依赖于[0,T]的加速度a。在每个样本时间都会考虑81个加速度曲线,即81个满足表达式(4)的轨迹,由此形成在目标车道上驾驶的他车的轨迹可行域。这81个轨迹符合速度约束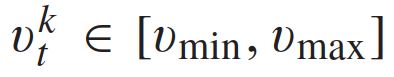 。将每一个轨迹表示为
。将每一个轨迹表示为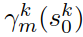 ,m = 1,2,……81,轨迹的集合记为
,m = 1,2,……81,轨迹的集合记为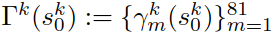 并入车辆的轨迹策略包括车道保持和变道,车道保持的轨迹生成 与(4) 类似,变道轨迹使用五阶多项式来表示[37]。即变道轨迹需求解可以建模为以下边值问题:找到系数
并入车辆的轨迹策略包括车道保持和变道,车道保持的轨迹生成 与(4) 类似,变道轨迹使用五阶多项式来表示[37]。即变道轨迹需求解可以建模为以下边值问题:找到系数 和
和 ,使5阶多项式满足相应的初值条件
,使5阶多项式满足相应的初值条件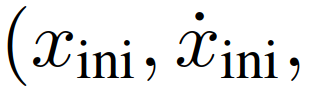
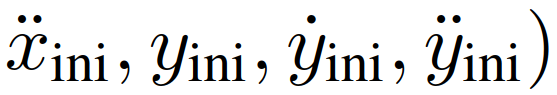 和终值条件
和终值条件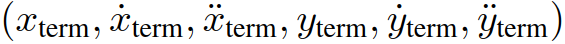 。(5)中的变量ζ表示连续时间,当前样本的ζ=0。同时假设1)车辆可以在规划范围内任何样本时间开始变道, 2)完整变道需要时间
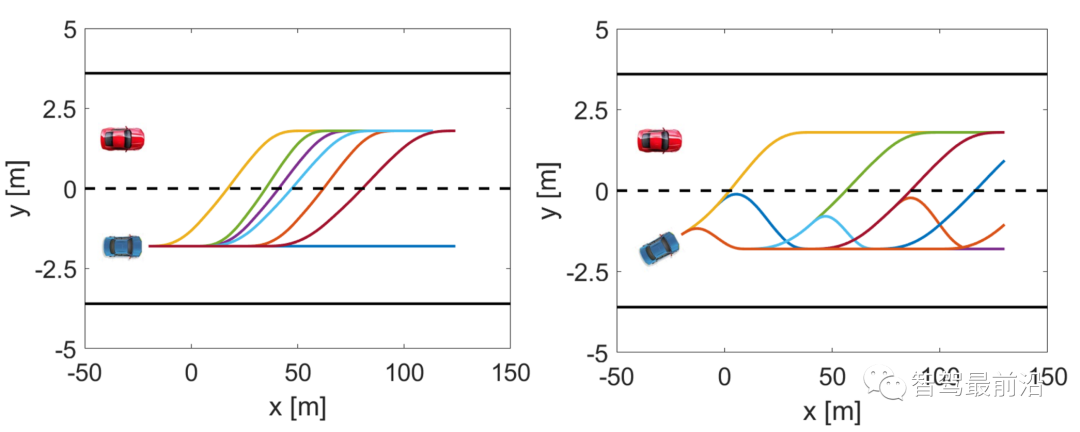
。(5)中的变量ζ表示连续时间,当前样本的ζ=0。同时假设1)车辆可以在规划范围内任何样本时间开始变道, 2)完整变道需要时间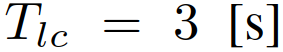 为常数[37]。允许车辆在变道过程随时终止变道行为,这代表当先前计划的变道变得不可行/安全时,司机“改变主意”。中止变道后的轨迹通过类似变道轨迹的方式生成。最后将车道保持、车道变更和放弃变道的轨迹拼接组合成162个轨迹,作为策略的可行域。提炼出轨迹特征为:1)是否/何时开始变道;2)是否/何时中止一个不适当的变道。图3为车辆没有开始变道时和当车辆在变道过程中时的轨迹采样集。将每个轨迹表示为
为常数[37]。允许车辆在变道过程随时终止变道行为,这代表当先前计划的变道变得不可行/安全时,司机“改变主意”。中止变道后的轨迹通过类似变道轨迹的方式生成。最后将车道保持、车道变更和放弃变道的轨迹拼接组合成162个轨迹,作为策略的可行域。提炼出轨迹特征为:1)是否/何时开始变道;2)是否/何时中止一个不适当的变道。图3为车辆没有开始变道时和当车辆在变道过程中时的轨迹采样集。将每个轨迹表示为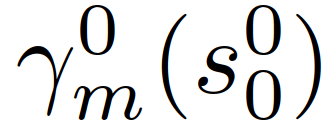 ,m = 1,2,……,162;轨迹集合为
,m = 1,2,……,162;轨迹集合为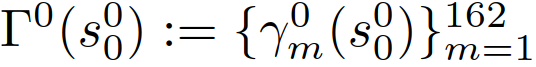 。综上定义了作为决策输出的可行轨迹。同时,对应这些轨迹的控制输入量的时间历史可以根据车辆动力学模型(1)计算。所规划的轨迹可以实际传递到下层的车辆运动控制器上。考虑基于MPC的自主自车轨迹规划策略,考虑信号交互车辆的存在:在每个样本时刻t,自车计算一个最优轨迹,
。综上定义了作为决策输出的可行轨迹。同时,对应这些轨迹的控制输入量的时间历史可以根据车辆动力学模型(1)计算。所规划的轨迹可以实际传递到下层的车辆运动控制器上。考虑基于MPC的自主自车轨迹规划策略,考虑信号交互车辆的存在:在每个样本时刻t,自车计算一个最优轨迹,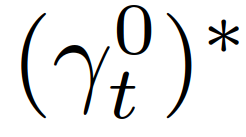 ,根据在规划范围内最大化其累积奖励:其中,
,根据在规划范围内最大化其累积奖励:其中,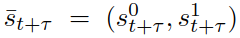 表示离散时刻t+τ的预测交通状态,而
表示离散时刻t+τ的预测交通状态,而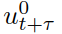 和
和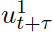 分别表示预测的自车和交互车辆在t+τ的控制输入。参数λ∈(0,1)是未来奖励的损益系数,即优先考虑当下的奖励。在(6)中,
分别表示预测的自车和交互车辆在t+τ的控制输入。参数λ∈(0,1)是未来奖励的损益系数,即优先考虑当下的奖励。在(6)中,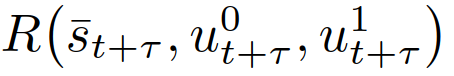 代表自车在t+τ时的奖励,如第II-C节所述,
代表自车在t+τ时的奖励,如第II-C节所述, 代表一组交通状态的安全值,用于执行严格的安全规范(如防碰撞、道路边界约束等)。在获得最优轨迹
代表一组交通状态的安全值,用于执行严格的安全规范(如防碰撞、道路边界约束等)。在获得最优轨迹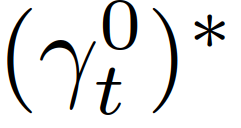 后,自车用与该轨迹对应的控制输入
后,自车用与该轨迹对应的控制输入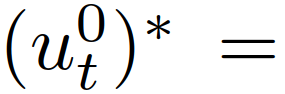
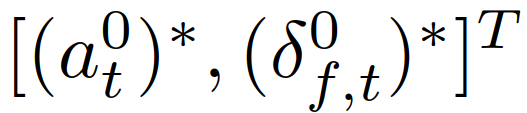 ,在一个采样周期内更新其状态,然后在下一个采样时间瞬间t + 1重复上述步骤。该部分介绍了本文中使用的领导者-跟随者博弈模型。为了简化博弈论模型的在线计算,使用模仿学习获得基于神经网络的显式模型,以在基于MPC的整体轨迹规划策略中在线预测交互车辆回应并入自车行为的轨迹。在本文中,我们考虑了基于成对的领导者-跟随者交互的参数理论模型来表示驾驶员的合作意图及其由此产生的车辆行为,称为领导者-跟随者博弈模型。该模型中,决定在另一辆车之前继续前进的车辆(或司机)是这对车中的领导者,而决定向另一辆车让步的车辆是这对车中的跟随者。领导者和跟随者使用不同的决策策略。这种领导者-跟随者博弈论模型最初是在[32]中提出的,此处简要回顾下该博弈论模型,以介绍它在高速公路强制并道场景中的应用。表示领导者和跟随者的轨迹分别为
,在一个采样周期内更新其状态,然后在下一个采样时间瞬间t + 1重复上述步骤。该部分介绍了本文中使用的领导者-跟随者博弈模型。为了简化博弈论模型的在线计算,使用模仿学习获得基于神经网络的显式模型,以在基于MPC的整体轨迹规划策略中在线预测交互车辆回应并入自车行为的轨迹。在本文中,我们考虑了基于成对的领导者-跟随者交互的参数理论模型来表示驾驶员的合作意图及其由此产生的车辆行为,称为领导者-跟随者博弈模型。该模型中,决定在另一辆车之前继续前进的车辆(或司机)是这对车中的领导者,而决定向另一辆车让步的车辆是这对车中的跟随者。领导者和跟随者使用不同的决策策略。这种领导者-跟随者博弈论模型最初是在[32]中提出的,此处简要回顾下该博弈论模型,以介绍它在高速公路强制并道场景中的应用。表示领导者和跟随者的轨迹分别为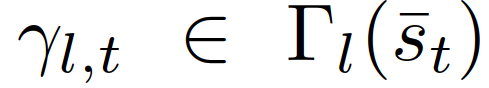 和
和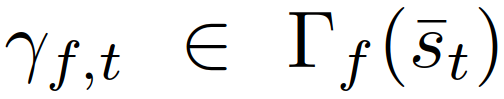 ,其中
,其中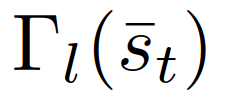 和
和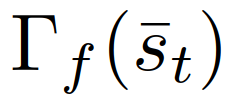 为领导者、跟随者的可行轨迹集。假设博弈双方都做出了最大化其累积奖励的决定,分别记为
为领导者、跟随者的可行轨迹集。假设博弈双方都做出了最大化其累积奖励的决定,分别记为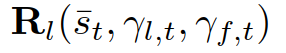 和
和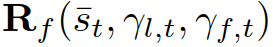 ,定义如下:其中
,定义如下:其中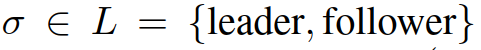 代表博弈中的角色,
代表博弈中的角色,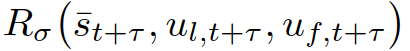 是领导者/跟随者的奖励函数,
是领导者/跟随者的奖励函数,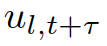 和
和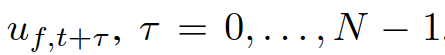 表示对应二者轨迹
表示对应二者轨迹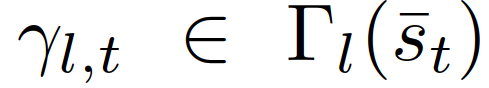 和
和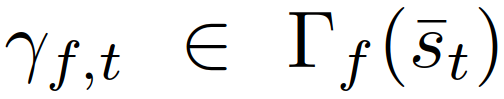 的控制输入量。具体来说,我们对领导者和跟随者的交互式决策过程进行建模如下:其中
的控制输入量。具体来说,我们对领导者和跟随者的交互式决策过程进行建模如下:其中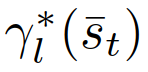 (区别于
(区别于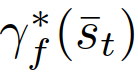 )是领导者(区别于跟随者)的最优轨迹,取决于当前交通状态,
)是领导者(区别于跟随者)的最优轨迹,取决于当前交通状态,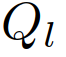 和
和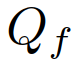 定义如下:其中
定义如下:其中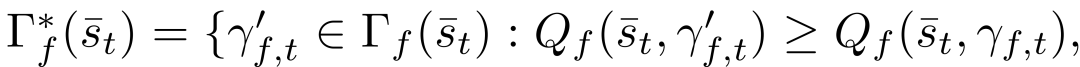
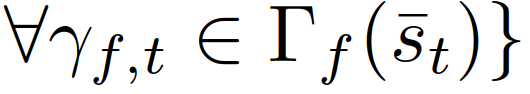 。决策模型(8)-(11)在强制并道中可以解释为:一个跟随者代表一个打算让步的司机。由于对其他司机的行动的不确定性,跟随者决定采取一个行动,通过(9)和(11)来最大化其的最坏情况下的奖励,他们假定其他驾驶员可以自由地采取行动。一个领导者则代表一个打算继续前进的司机,他们假设另一个司机会屈服。因此,领导者使用跟随者模型来预测另一个司机的行动,并通过(8)和(10),在预测的跟随者的行动下最大化领导者自己的奖励。这种领导者-跟随者博弈模型部分源自斯塔克尔伯格博弈模型[38],但放宽了不适用于驾驶员交互的一些假设。可以参考[32]来更详细的了解领导跟随者博弈模型以及它在多车辆场景中建模驾驶员交互的有效性。请注意,该模型并不意味着一个领导者车辆总是迫使并入车辆在其后并道或跟随者车辆总让并入车辆在其前并道,在以下举例的两个情况中,并道车辆可能在领导者车辆前并道:1)并道车辆在领导者车辆前面,有足够大的距离,允许安全并道。2)正在并入的车辆即将到达其车道的尽头。因为离开道路产生一个大的惩罚(见第二节-c),因此只要自车的并入不导致碰撞(碰撞的惩罚大于离开道路),自车即可以选择并道在来车之前以避免大的惩罚,。以上表明,在我们的决策模型(8)-(11)中,领导者跟随者的角色并不是由车辆的空间位置来分配的(领导者不一定是前面的车辆)。此外,模型允许自车迫使目标车道交通流让它并道:自车接近目标车道时,将越来越倾向于并道以避免离开道路受到惩罚,此时自车会在目标车道的所有交互车辆都是领导者或目前的并入间隙不够大、并入不够舒适时仍然采取并入动作。模型(8)-(11)表明领导者身份的交互车辆能够预测并入车辆接下来的并入动机。随后,并入车辆为了自身的安全和舒适,也会放慢速度扩大车距,从而保证并道。(8)-(11)能够基于驾驶员的意图和当前交通状态信息预测他车的决策和轨迹,即领导者的最优行动策略
。决策模型(8)-(11)在强制并道中可以解释为:一个跟随者代表一个打算让步的司机。由于对其他司机的行动的不确定性,跟随者决定采取一个行动,通过(9)和(11)来最大化其的最坏情况下的奖励,他们假定其他驾驶员可以自由地采取行动。一个领导者则代表一个打算继续前进的司机,他们假设另一个司机会屈服。因此,领导者使用跟随者模型来预测另一个司机的行动,并通过(8)和(10),在预测的跟随者的行动下最大化领导者自己的奖励。这种领导者-跟随者博弈模型部分源自斯塔克尔伯格博弈模型[38],但放宽了不适用于驾驶员交互的一些假设。可以参考[32]来更详细的了解领导跟随者博弈模型以及它在多车辆场景中建模驾驶员交互的有效性。请注意,该模型并不意味着一个领导者车辆总是迫使并入车辆在其后并道或跟随者车辆总让并入车辆在其前并道,在以下举例的两个情况中,并道车辆可能在领导者车辆前并道:1)并道车辆在领导者车辆前面,有足够大的距离,允许安全并道。2)正在并入的车辆即将到达其车道的尽头。因为离开道路产生一个大的惩罚(见第二节-c),因此只要自车的并入不导致碰撞(碰撞的惩罚大于离开道路),自车即可以选择并道在来车之前以避免大的惩罚,。以上表明,在我们的决策模型(8)-(11)中,领导者跟随者的角色并不是由车辆的空间位置来分配的(领导者不一定是前面的车辆)。此外,模型允许自车迫使目标车道交通流让它并道:自车接近目标车道时,将越来越倾向于并道以避免离开道路受到惩罚,此时自车会在目标车道的所有交互车辆都是领导者或目前的并入间隙不够大、并入不够舒适时仍然采取并入动作。模型(8)-(11)表明领导者身份的交互车辆能够预测并入车辆接下来的并入动机。随后,并入车辆为了自身的安全和舒适,也会放慢速度扩大车距,从而保证并道。(8)-(11)能够基于驾驶员的意图和当前交通状态信息预测他车的决策和轨迹,即领导者的最优行动策略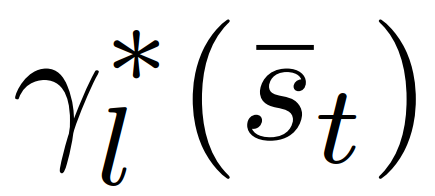 、跟随者的最优行动策略
、跟随者的最优行动策略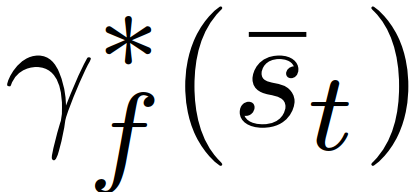 都可通过(8)-(11)获得。但 (8)-(11)的重复在线计算会很耗时。因此,我们将使用模仿学习显式地表示
都可通过(8)-(11)获得。但 (8)-(11)的重复在线计算会很耗时。因此,我们将使用模仿学习显式地表示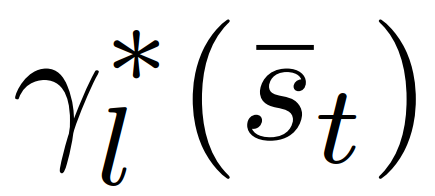 和
和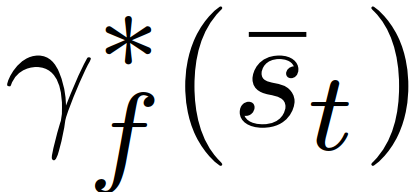 。参考[39],我们利用监督学习(具体为使用模仿学习)表示
。参考[39],我们利用监督学习(具体为使用模仿学习)表示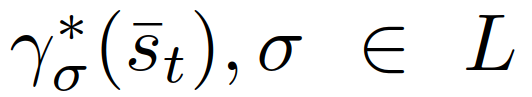 。模仿学习属于监督学习问题,代理将通过观察专家的行为来学习一个策略。专家可以是人工或人工智能代理,在我们的工作中,由(8)-(11)获得的即专家策略
。模仿学习属于监督学习问题,代理将通过观察专家的行为来学习一个策略。专家可以是人工或人工智能代理,在我们的工作中,由(8)-(11)获得的即专家策略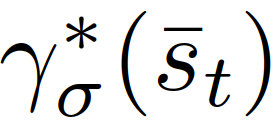 。我们利用“数据集聚合”算法[40]获得了一个模拟的策略
。我们利用“数据集聚合”算法[40]获得了一个模拟的策略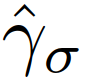 。
。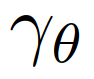 表示使用θ(神经网络权重)参数化的策略,
表示使用θ(神经网络权重)参数化的策略,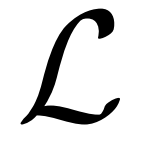 表示损失函数,关于模仿学习和“数据集聚合”算法详见[39]和[40]。学习(8)-(11)的模仿学习策略可以在了解驾驶员合作意图的情况下预测他车的决策和未来的发展轨迹。然而,在给定的交通场景中,我们可能事先不知道其他司机的合作意图,因为司机的意图不仅取决于交通情况(例如,两辆车之间的相对位置和速度),还取决于驾驶员的风格/类型(例如,攻击性和保守性)。我们将他车合作意图的不确定性建模为潜在变量,在自动驾驶汽车规划和控制问题中将利用估计他车的合作意图以及使用预测控制方法获得最优轨迹。下面我们描述了在合作意图不确定下的高速公路强制并道决策算法,即领导者-跟随博弈控制器(LFGC)。在强制并道过程中,我们生成一个如本节所述的其他驾驶员的合作意图估计,基于该估计将(6)建模为成对交互的多车控制策略。使用引导跟随者博弈,根据对他车驾驶员的合作意图进行行为建模。屈服的车辆建模为博弈中的跟随者,继续(不屈服)的车辆建模为领导者。即,可以通过估计交互车辆在领导者-跟随者博弈中的角色来估计交互车辆的合作意图。为了实现这一点,我们考虑了交通动力学模型(2)以及领导者或跟随者的最佳行动(8)和(9)。从自车的角度来看,交互车辆是在进行领导者-跟随者博弈,动态交通模型可以写成其中
表示损失函数,关于模仿学习和“数据集聚合”算法详见[39]和[40]。学习(8)-(11)的模仿学习策略可以在了解驾驶员合作意图的情况下预测他车的决策和未来的发展轨迹。然而,在给定的交通场景中,我们可能事先不知道其他司机的合作意图,因为司机的意图不仅取决于交通情况(例如,两辆车之间的相对位置和速度),还取决于驾驶员的风格/类型(例如,攻击性和保守性)。我们将他车合作意图的不确定性建模为潜在变量,在自动驾驶汽车规划和控制问题中将利用估计他车的合作意图以及使用预测控制方法获得最优轨迹。下面我们描述了在合作意图不确定下的高速公路强制并道决策算法,即领导者-跟随博弈控制器(LFGC)。在强制并道过程中,我们生成一个如本节所述的其他驾驶员的合作意图估计,基于该估计将(6)建模为成对交互的多车控制策略。使用引导跟随者博弈,根据对他车驾驶员的合作意图进行行为建模。屈服的车辆建模为博弈中的跟随者,继续(不屈服)的车辆建模为领导者。即,可以通过估计交互车辆在领导者-跟随者博弈中的角色来估计交互车辆的合作意图。为了实现这一点,我们考虑了交通动力学模型(2)以及领导者或跟随者的最佳行动(8)和(9)。从自车的角度来看,交互车辆是在进行领导者-跟随者博弈,动态交通模型可以写成其中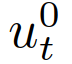 是自车的控制,
是自车的控制,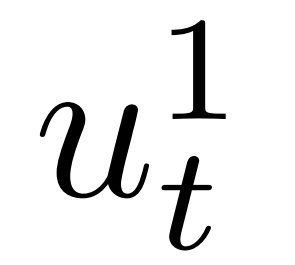 是交互车辆的控制,由领导者跟随者博弈得到,
是交互车辆的控制,由领导者跟随者博弈得到,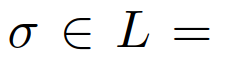 {领导者,跟随者}代表跟随者或领导者,并且
{领导者,跟随者}代表跟随者或领导者,并且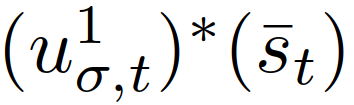 第一个控制输入,对应(8)(9)中
第一个控制输入,对应(8)(9)中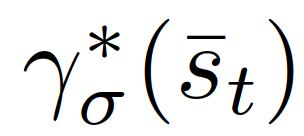 的最优轨迹。现在(14)的唯一输入是对自车的控制
的最优轨迹。现在(14)的唯一输入是对自车的控制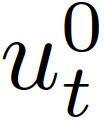 。考虑到现实中,他车的决策并不一定遵循从(8)和(9)中计算出的最优策略,因此加入高斯噪声,假设系统按照(14)工作:其中
。考虑到现实中,他车的决策并不一定遵循从(8)和(9)中计算出的最优策略,因此加入高斯噪声,假设系统按照(14)工作:其中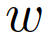 为均值和协方差为0的加性高斯噪声。假设自车对σ有一个先验信念,表示为
为均值和协方差为0的加性高斯噪声。假设自车对σ有一个先验信念,表示为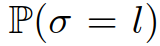 ,其中
,其中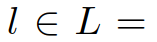 {领导者,跟随者}。然后根据所有以前的交通状态和自车所采取的所有行动自车需要计算或维持对交互车辆的领导者或跟随者角色的后验信念,
{领导者,跟随者}。然后根据所有以前的交通状态和自车所采取的所有行动自车需要计算或维持对交互车辆的领导者或跟随者角色的后验信念,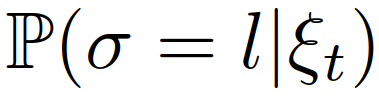 。利用[41]中提出的混合估计算法,可以计算交互车辆的领导者或跟随者角色的条件后验信念。具体来说,识别交互车辆的领导者或跟随者角色可以表示为:其中
。利用[41]中提出的混合估计算法,可以计算交互车辆的领导者或跟随者角色的条件后验信念。具体来说,识别交互车辆的领导者或跟随者角色可以表示为:其中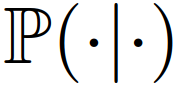 为条件概率;
为条件概率;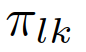 为作用车角色从
为作用车角色从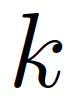 到
到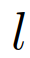 的转移概率;
的转移概率;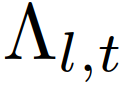 为作用车角色
为作用车角色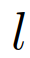 的似然函数,定义为:式中,
的似然函数,定义为:式中,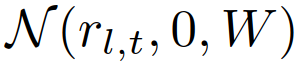 为正态分布的概率密度函数,均值为0,协方差W在
为正态分布的概率密度函数,均值为0,协方差W在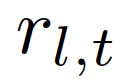 评估;
评估;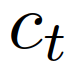 为归一化常数。假设交互车辆的角色在并道期间保持不变,即当
为归一化常数。假设交互车辆的角色在并道期间保持不变,即当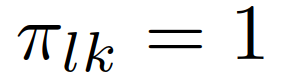 时
时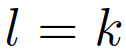 ,当
,当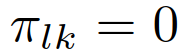 时,交互车辆的领导者或跟随者角色的后验信念可以使用以下方程更新:其中
时,交互车辆的领导者或跟随者角色的后验信念可以使用以下方程更新:其中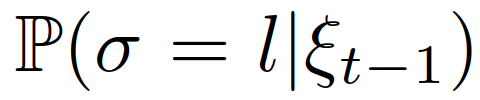 是交互车辆的领导者或跟随者的角色的先验信念。当交通繁忙时,高速公路上可能存在多辆车辆干扰自车的并道,如图1所示。一个低复杂度的解决方案是,自车只考虑与第一辆车的交互,第一辆车远离后开始与第二辆车的交互。然而,这可能会导致对后车辆意图的估计推迟,从而致使自车失去并道的机会。另一种解决方案是同时与多辆车辆进行交互。这时需要构建模型来预测交互车辆的行为。虽然第三节中描述的2人领导-跟随博弈可以通过考虑多层次决策层次来扩展到多人领导者-跟随者博弈,但随着玩家数量的增加模型复杂度将呈指数级增长。超过3个玩家时,即很难获得斯塔克尔伯格平衡[42]。因此,我们提出了一种计算上易于处理的方法,通过考虑成对交互,将框架扩展到多车辆交互。当有m个相互作用的车辆时,我们考虑自车和每个相互作用的车辆的成对交互,然后构造m个包含自车和第k个他车状态的交通状态,表示为
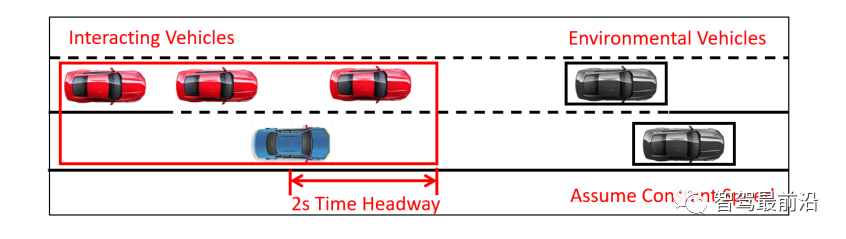
是交互车辆的领导者或跟随者的角色的先验信念。当交通繁忙时,高速公路上可能存在多辆车辆干扰自车的并道,如图1所示。一个低复杂度的解决方案是,自车只考虑与第一辆车的交互,第一辆车远离后开始与第二辆车的交互。然而,这可能会导致对后车辆意图的估计推迟,从而致使自车失去并道的机会。另一种解决方案是同时与多辆车辆进行交互。这时需要构建模型来预测交互车辆的行为。虽然第三节中描述的2人领导-跟随博弈可以通过考虑多层次决策层次来扩展到多人领导者-跟随者博弈,但随着玩家数量的增加模型复杂度将呈指数级增长。超过3个玩家时,即很难获得斯塔克尔伯格平衡[42]。因此,我们提出了一种计算上易于处理的方法,通过考虑成对交互,将框架扩展到多车辆交互。当有m个相互作用的车辆时,我们考虑自车和每个相互作用的车辆的成对交互,然后构造m个包含自车和第k个他车状态的交通状态,表示为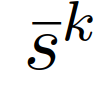 ,
,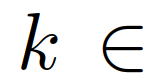
 ,每个的动态模型由下式给出:类似地,我们可以用
,每个的动态模型由下式给出:类似地,我们可以用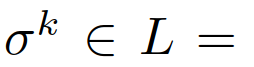 {领导者,跟随者}表示第k个交互车辆的成对领导者或跟随者角色,用
{领导者,跟随者}表示第k个交互车辆的成对领导者或跟随者角色,用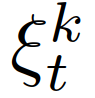 表示自车所有之前的成对交通状态和行动的集合,即,然后我们可以利用(19)来更新每个交互车辆的领导者或跟随者角色的信念,
表示自车所有之前的成对交通状态和行动的集合,即,然后我们可以利用(19)来更新每个交互车辆的领导者或跟随者角色的信念,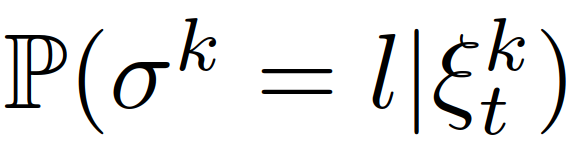 ,
,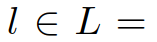 {领导者,跟随者}。(6)中基于MPC的控制策略可以重新表述为:其中,
{领导者,跟随者}。(6)中基于MPC的控制策略可以重新表述为:其中,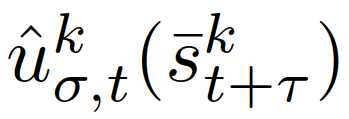 是(12)中训练策略
是(12)中训练策略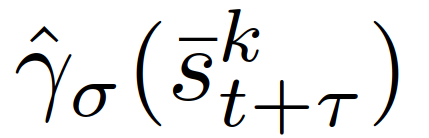 的轨迹对应的第一个控制输入,ε∈[0,1]表示(用户指定的)所需的约束满足概率水平。其中,
的轨迹对应的第一个控制输入,ε∈[0,1]表示(用户指定的)所需的约束满足概率水平。其中,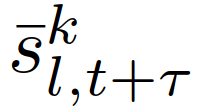 为给定交互车辆的角色为
为给定交互车辆的角色为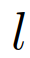 的预测交通状态,其中,
的预测交通状态,其中,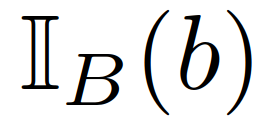 为集合B中b的指示器函数。请注意,(22)中的最后一个约束强制执行了以下条件,这意味着任何成对的交互作用进入不安全状态(例如,碰撞和离开道路边界)的概率都小于ε。为了推导(26),我们首先表示事件
为集合B中b的指示器函数。请注意,(22)中的最后一个约束强制执行了以下条件,这意味着任何成对的交互作用进入不安全状态(例如,碰撞和离开道路边界)的概率都小于ε。为了推导(26),我们首先表示事件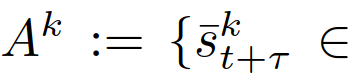
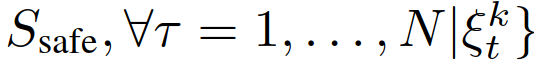 然后1) (6)中的 为未知,而在(22)中,它们是基于模仿学习的训练策略获得的;2)将(6)中累积奖励的最大化改为(22)中期望累积奖励的最大化,以解释交互车辆的领导者/跟随者角色的概率信念;3)期望累积奖励改变为所有成对交互的期望奖励之和,以解释多辆车辆的不确定行为(便于计算);4)硬约束变为概率的机会约束,以ε∈[0,1]为参数。决策算法进行如下:在采样时间t时,自车测量每组交互对的当前状态,并将它们与之前的控制输入量一起添加到观测向量
然后1) (6)中的 为未知,而在(22)中,它们是基于模仿学习的训练策略获得的;2)将(6)中累积奖励的最大化改为(22)中期望累积奖励的最大化,以解释交互车辆的领导者/跟随者角色的概率信念;3)期望累积奖励改变为所有成对交互的期望奖励之和,以解释多辆车辆的不确定行为(便于计算);4)硬约束变为概率的机会约束,以ε∈[0,1]为参数。决策算法进行如下:在采样时间t时,自车测量每组交互对的当前状态,并将它们与之前的控制输入量一起添加到观测向量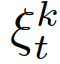 中。对每辆车的领导者或跟随者角色的信念根据(19)进行更新。然后,利用基于MPC的控制策略(22),通过搜索第2-D节中引入的所有轨迹,得到最优轨迹
中。对每辆车的领导者或跟随者角色的信念根据(19)进行更新。然后,利用基于MPC的控制策略(22),通过搜索第2-D节中引入的所有轨迹,得到最优轨迹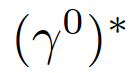 ,自车在一个采样周期内应用第一个控制输入来更新其状态。整个过程将在下一次采样时重复进行。需要注意的是,控制策略(22)是“交互感知”的,原因如下:1)它基于领导者-跟随者博弈论模型(8)-(11)预测不同交互意图下他车的轨迹。2)这些预测都是闭环式的。具体来说,对应自车的不同轨迹规划
,自车在一个采样周期内应用第一个控制输入来更新其状态。整个过程将在下一次采样时重复进行。需要注意的是,控制策略(22)是“交互感知”的,原因如下:1)它基于领导者-跟随者博弈论模型(8)-(11)预测不同交互意图下他车的轨迹。2)这些预测都是闭环式的。具体来说,对应自车的不同轨迹规划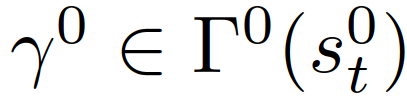 ,他车特定意图下的轨迹预测也是不同的。这种情况是因为预测的他车的行为依赖于交通状态,而预测的交通状态依赖于自车的规划轨迹。3)(22)中的目标函数是一个条件期望,表示安全的约束是一个条件概率,两者都基于他车意图(即领导者或跟随者)的最新估计,
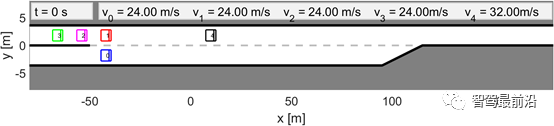
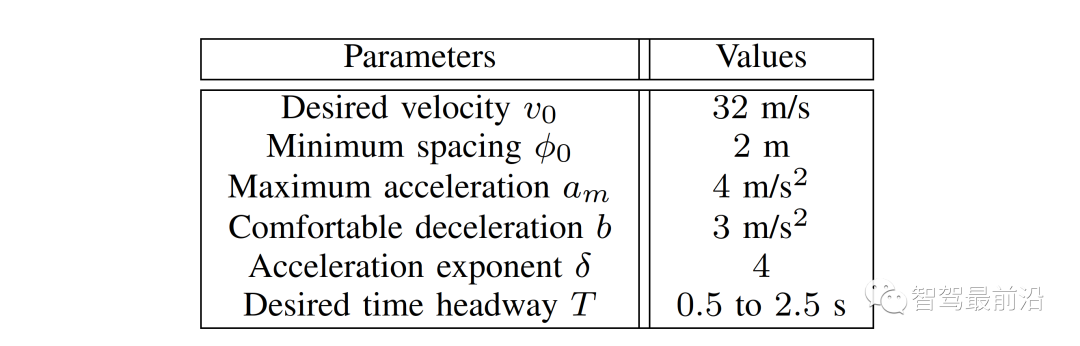
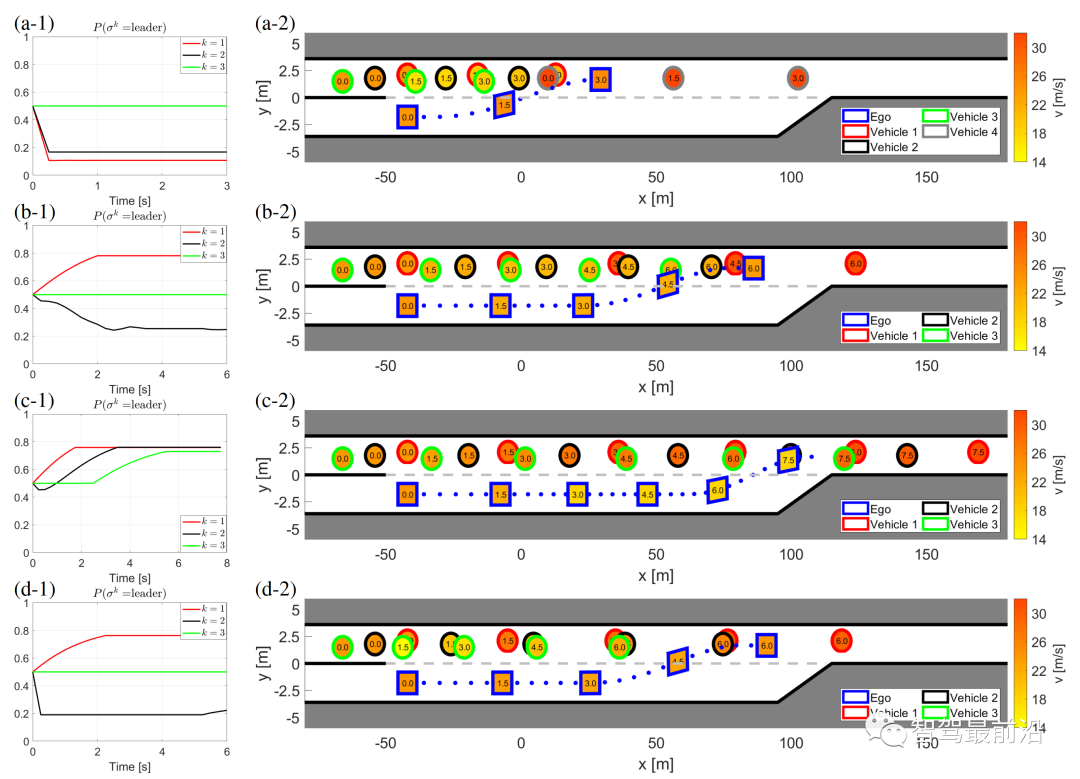
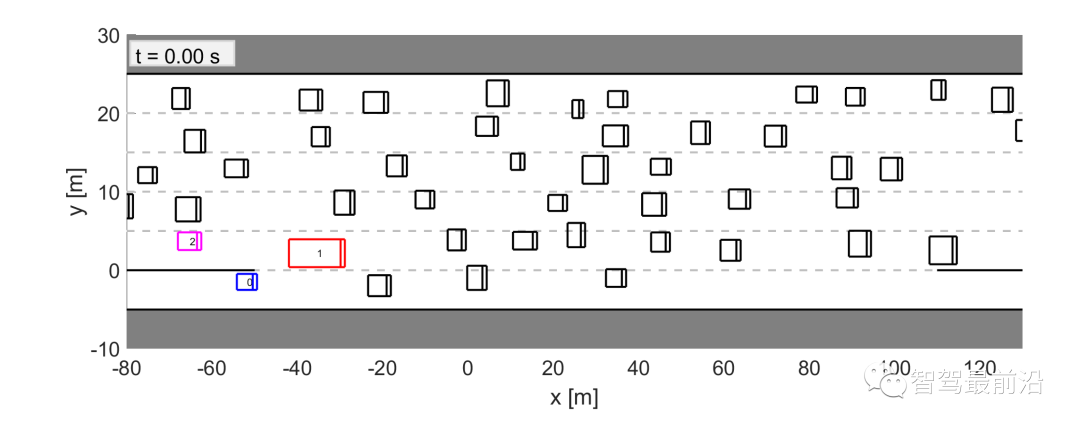
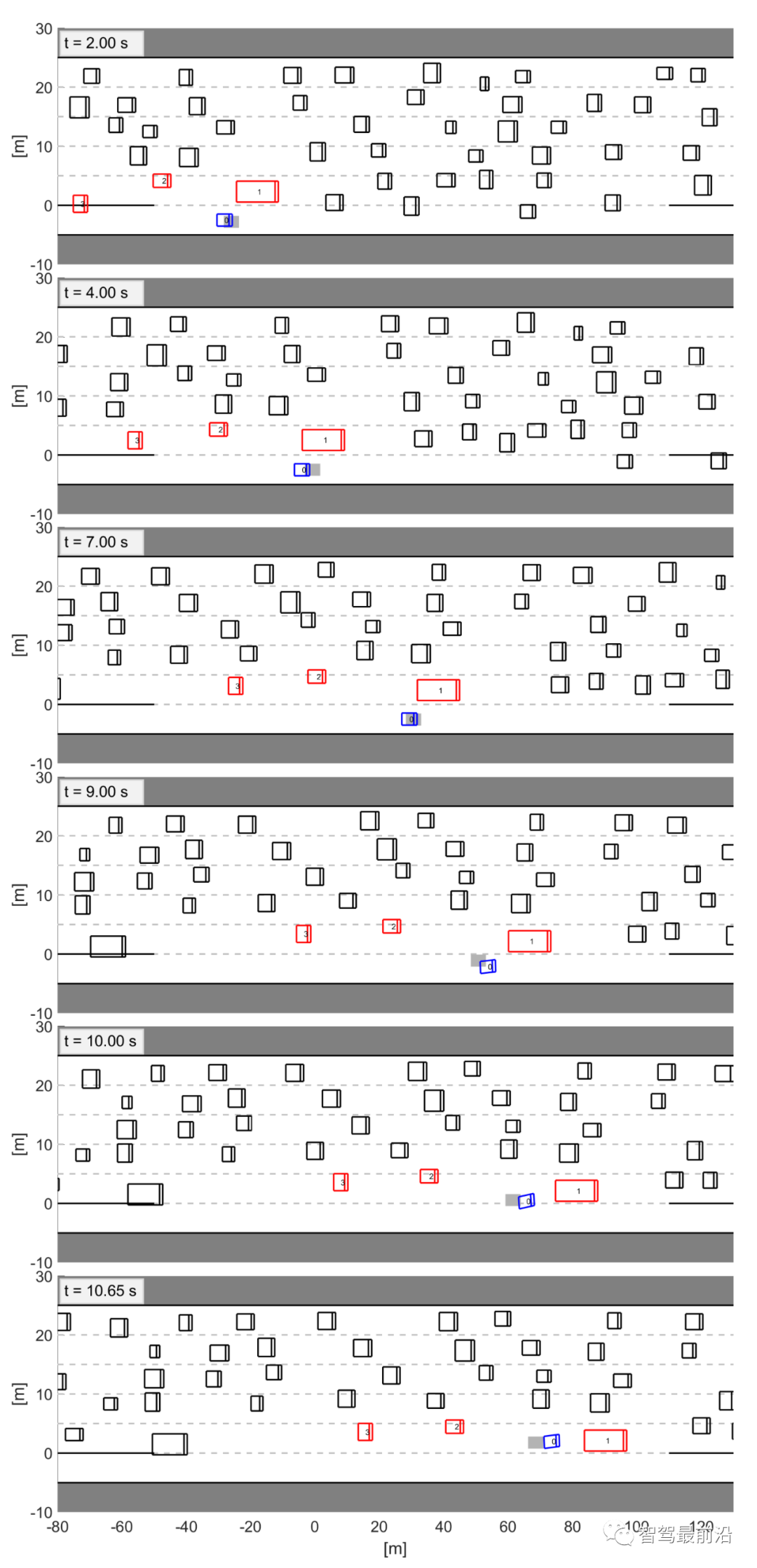
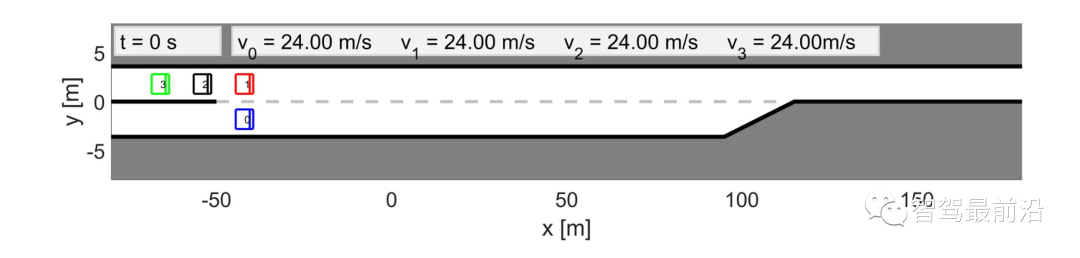
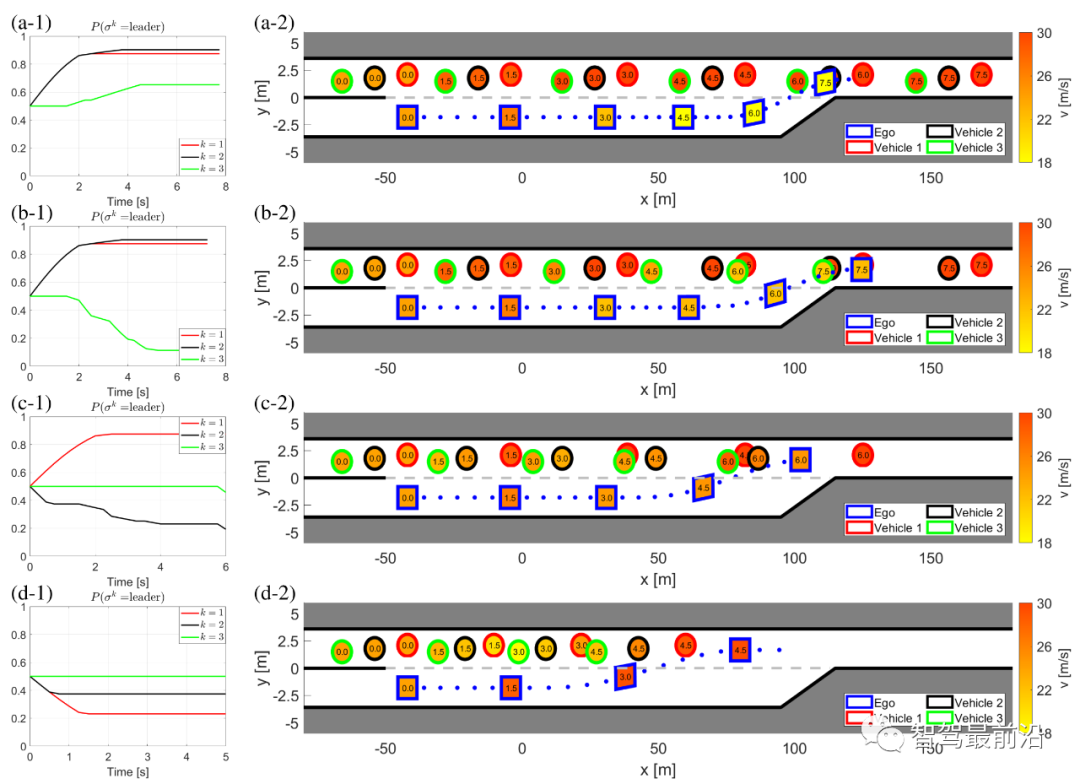
,他车特定意图下的轨迹预测也是不同的。这种情况是因为预测的他车的行为依赖于交通状态,而预测的交通状态依赖于自车的规划轨迹。3)(22)中的目标函数是一个条件期望,表示安全的约束是一个条件概率,两者都基于他车意图(即领导者或跟随者)的最新估计,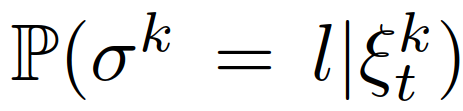 。同时,根据他车之前的交互行为来估计他车意图。在本节中,我们将展示领跟随博弈控制器(LFGC)应用于自动驾驶车辆强制并道问题的验证结果。我们具体考虑了三个模拟验证,在这些模拟中,LFGC假设交互车辆与自车进行领导者-跟随者博弈,并估计他们在博弈中的领导者/跟随者角色。我们还假设,一旦进入强制变道情况,自车用转向信号对准车道,宣布其并道意图,并开始强制并道过程。因此,交互他车会意识到自车的并道意图,并做出相应的反应。我们首先在领导者-跟随者博弈中,使用由领导者或跟随者控制的交互车辆来验证LFGC。然后,我们测试了LFGC与由其他类型的司机或实际交通数据控制的交互车辆。此外,我们测试了通过智能驾驶员模型对交互车辆(IDM)进行控制的情况,以及交互车辆遵循下一代模拟网站[34]中实际的美国101高速公路交通数据。我们的模拟是在Intel Xeon E3-1246 v3 @ 3.50 GHz CPU和16 GB内存的PC上的MATLAB R2019a平台上执行的。首先我们使用领导者/跟随者模拟和控制互动车辆,测试LFGC。我们所考虑的场景如图4所示,加速车道上的自动自车(蓝色)在加速车道结束前需要并道到高速公路上,而其他多辆车辆(红色、粉色、绿色)目前正在高速公路上行驶。如图4所示,自车通过偏向车道标记和闪烁的转向信号来开始强制并道过程。在这种情况下,自动驾驶车辆需要与他车进行交互,以实现安全并道。图4 高速公路强制并道场景下领导者/跟随者控制交互车辆的LFGC验证场景图经过试验,自车能=正确地识别出互动车辆的意图(即能正确划分交互他车为领导者/跟随者)图5 使用LFGC与不同领导者和跟随者组合的他车的交互结果(b) 他车为1领导者(车辆1)和2跟随者(车辆2和3);(c) 他车为两个领导者(车辆1和2)和一个跟随者(车辆3);左栏(a-1)到(d-1)显示了自车对他车在博弈中的领导者的信念。右列(a-2)到(d-2)显示了在这个强制并道过程中自车和他车行为的时间历史结果。具体来说,在右栏中,每个块的边界线颜色区分不同的车辆,块中的数字表示时间以秒为单位,每个块的颜色描述该时刻的车辆速度,蓝色虚线表示自车的轨迹。请注意,车辆1-3有相同的纵向位置,图中添加了一些纵向偏移量以更好地区分。对于LFGC,规划范围为N = 4,机会约束参数为ε = 0.1。请注意,较大的N可能会导致更好的长期性能,但也会导致更长的计算时间,而较小的N可能会强调直接的好处,因此在许多情况下无法合并。对于本文中考虑的高速公路强制合并,一般需要选择N,使其超过车道变更的持续时间(即
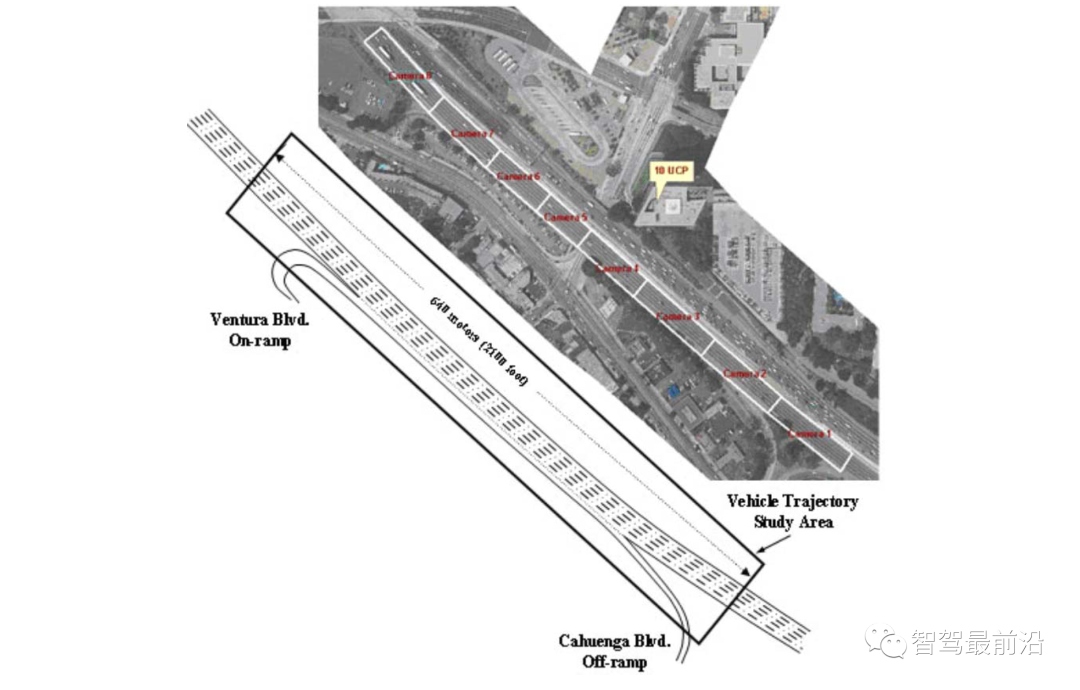
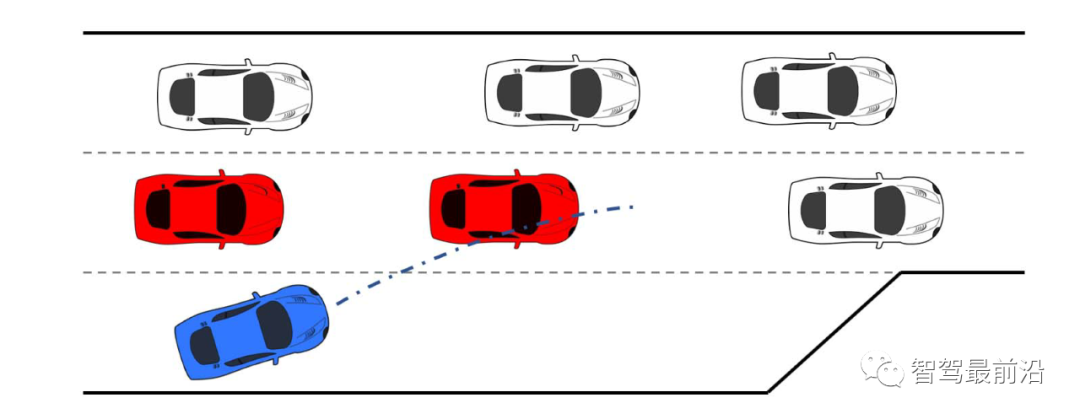
。同时,根据他车之前的交互行为来估计他车意图。在本节中,我们将展示领跟随博弈控制器(LFGC)应用于自动驾驶车辆强制并道问题的验证结果。我们具体考虑了三个模拟验证,在这些模拟中,LFGC假设交互车辆与自车进行领导者-跟随者博弈,并估计他们在博弈中的领导者/跟随者角色。我们还假设,一旦进入强制变道情况,自车用转向信号对准车道,宣布其并道意图,并开始强制并道过程。因此,交互他车会意识到自车的并道意图,并做出相应的反应。我们首先在领导者-跟随者博弈中,使用由领导者或跟随者控制的交互车辆来验证LFGC。然后,我们测试了LFGC与由其他类型的司机或实际交通数据控制的交互车辆。此外,我们测试了通过智能驾驶员模型对交互车辆(IDM)进行控制的情况,以及交互车辆遵循下一代模拟网站[34]中实际的美国101高速公路交通数据。我们的模拟是在Intel Xeon E3-1246 v3 @ 3.50 GHz CPU和16 GB内存的PC上的MATLAB R2019a平台上执行的。首先我们使用领导者/跟随者模拟和控制互动车辆,测试LFGC。我们所考虑的场景如图4所示,加速车道上的自动自车(蓝色)在加速车道结束前需要并道到高速公路上,而其他多辆车辆(红色、粉色、绿色)目前正在高速公路上行驶。如图4所示,自车通过偏向车道标记和闪烁的转向信号来开始强制并道过程。在这种情况下,自动驾驶车辆需要与他车进行交互,以实现安全并道。图4 高速公路强制并道场景下领导者/跟随者控制交互车辆的LFGC验证场景图经过试验,自车能=正确地识别出互动车辆的意图(即能正确划分交互他车为领导者/跟随者)图5 使用LFGC与不同领导者和跟随者组合的他车的交互结果(b) 他车为1领导者(车辆1)和2跟随者(车辆2和3);(c) 他车为两个领导者(车辆1和2)和一个跟随者(车辆3);左栏(a-1)到(d-1)显示了自车对他车在博弈中的领导者的信念。右列(a-2)到(d-2)显示了在这个强制并道过程中自车和他车行为的时间历史结果。具体来说,在右栏中,每个块的边界线颜色区分不同的车辆,块中的数字表示时间以秒为单位,每个块的颜色描述该时刻的车辆速度,蓝色虚线表示自车的轨迹。请注意,车辆1-3有相同的纵向位置,图中添加了一些纵向偏移量以更好地区分。对于LFGC,规划范围为N = 4,机会约束参数为ε = 0.1。请注意,较大的N可能会导致更好的长期性能,但也会导致更长的计算时间,而较小的N可能会强调直接的好处,因此在许多情况下无法合并。对于本文中考虑的高速公路强制合并,一般需要选择N,使其超过车道变更的持续时间(即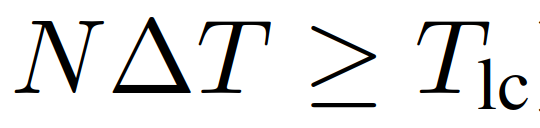 )。图5(a)显示了自车与三个领导者互动时的结果。自车能够捕捉到互动车辆的意图,即所有车辆都更有可能成为博弈中的领导者,如图5(a-1)所示。在获得这些信息后,自车决定在t = 1 [s]后减速,并在所有交互的车辆经过后等待合并。当自车与一个领导者(车辆1)和两个跟随者(车辆2和3)交互时,自车正确识别互动车辆的意图,如图5(b-1)所示。然后在t = 1 [s]后,自车开始减速,并在车辆1和车辆2之间成功合并,如图5(b-2)所示。如图5所示,(c)是自车与两个领导者(车辆1和2)和一个跟随者(车辆3)交互的结果。在这种情况下,自车观察到车辆1和2加速而不屈服,所以自车决定减速,并在车辆2和3之间合并。当自车与三个跟随者互动时,我们也进行了测试,结果如图5(d)所示,自车观察所有产生意图的车辆,在所有互动的车辆前面加速和合并。在每个时间步长中,求解(22)的平均计算时间为0.182 [s]。对于图5所示的所有案例,初始化的信念是相同的,这意味着自车不提前知道互动的载体是领导者还是跟随者。因此,自车依赖于它的观察来估计互动载体的领导者/跟随者的角色。在领导者-跟随者博弈中,当所有互动车辆都被领导者/跟随者控制时,LFGC可以捕捉互动车辆的意图并做出相应的决策。第5-A节中显示的验证结果假设他车根据领导者-跟随者的博弈做出决策。LFGC估计其他司机在博弈中的角色,并做出相应的决定。这意味着第5-A节中的环境的行为与LFGC所期望的一样。然而,其他司机的实际行为可能不同于领导者-跟随者博弈的政策。因此,我们进一步研究该框架如何在他车使用智能驾驶员模型(IDM)时做出响应。在本节使用IDM控制他车,并与自车交互。自车仍由LFGC控制,并试图通过估计其相应的领导者或跟随者角色来估计互动车辆的意图。IDM是一个连续时间的汽车跟踪模型,由(27)到(29)[43]来定义。其中
)。图5(a)显示了自车与三个领导者互动时的结果。自车能够捕捉到互动车辆的意图,即所有车辆都更有可能成为博弈中的领导者,如图5(a-1)所示。在获得这些信息后,自车决定在t = 1 [s]后减速,并在所有交互的车辆经过后等待合并。当自车与一个领导者(车辆1)和两个跟随者(车辆2和3)交互时,自车正确识别互动车辆的意图,如图5(b-1)所示。然后在t = 1 [s]后,自车开始减速,并在车辆1和车辆2之间成功合并,如图5(b-2)所示。如图5所示,(c)是自车与两个领导者(车辆1和2)和一个跟随者(车辆3)交互的结果。在这种情况下,自车观察到车辆1和2加速而不屈服,所以自车决定减速,并在车辆2和3之间合并。当自车与三个跟随者互动时,我们也进行了测试,结果如图5(d)所示,自车观察所有产生意图的车辆,在所有互动的车辆前面加速和合并。在每个时间步长中,求解(22)的平均计算时间为0.182 [s]。对于图5所示的所有案例,初始化的信念是相同的,这意味着自车不提前知道互动的载体是领导者还是跟随者。因此,自车依赖于它的观察来估计互动载体的领导者/跟随者的角色。在领导者-跟随者博弈中,当所有互动车辆都被领导者/跟随者控制时,LFGC可以捕捉互动车辆的意图并做出相应的决策。第5-A节中显示的验证结果假设他车根据领导者-跟随者的博弈做出决策。LFGC估计其他司机在博弈中的角色,并做出相应的决定。这意味着第5-A节中的环境的行为与LFGC所期望的一样。然而,其他司机的实际行为可能不同于领导者-跟随者博弈的政策。因此,我们进一步研究该框架如何在他车使用智能驾驶员模型(IDM)时做出响应。在本节使用IDM控制他车,并与自车交互。自车仍由LFGC控制,并试图通过估计其相应的领导者或跟随者角色来估计互动车辆的意图。IDM是一个连续时间的汽车跟踪模型,由(27)到(29)[43]来定义。其中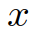 为纵向位置;
为纵向位置;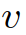 为纵向速度;
为纵向速度;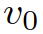 为车辆的期望速度;
为车辆的期望速度;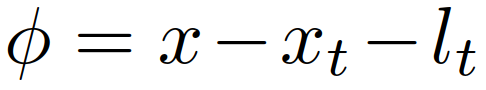 为跟车距离,
为跟车距离,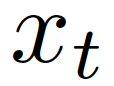 为目标车辆的位置,
为目标车辆的位置,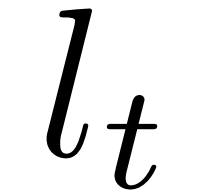 为目标车辆的长度;
为目标车辆的长度;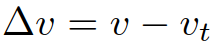 是车辆与目标车辆的速度差;
是车辆与目标车辆的速度差;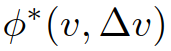 根据:其中,
根据:其中,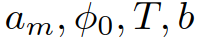 为IDM模型的参数。这些参数的物理解释是最大加速度
为IDM模型的参数。这些参数的物理解释是最大加速度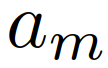 、跟随距离
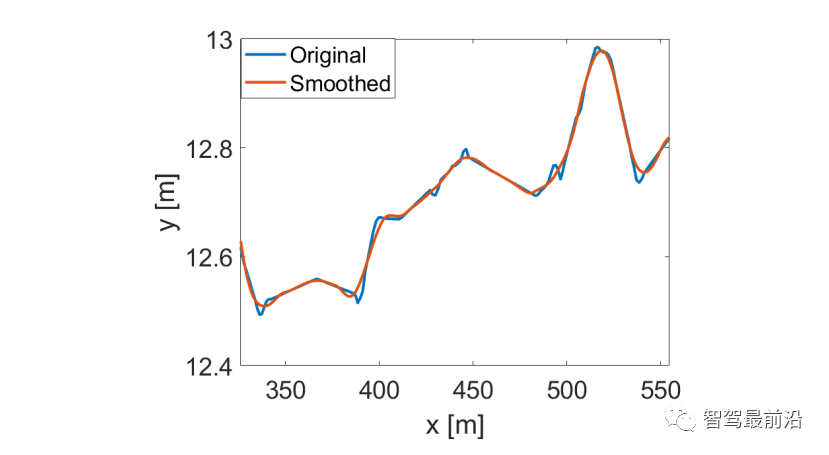
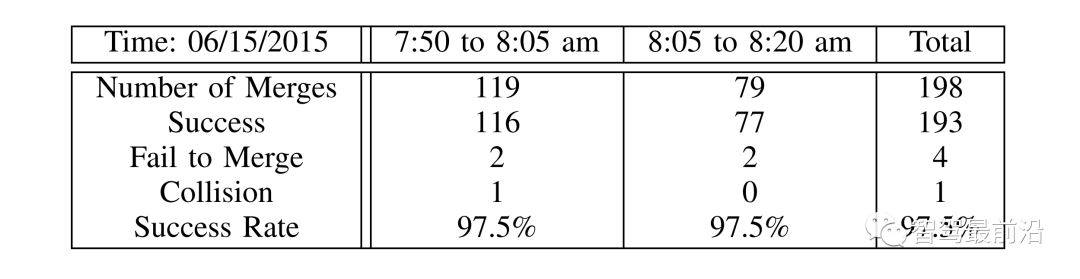
、跟随距离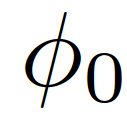 的最小车辆、期望的时间T和舒适减速度b。我们考虑了图6中所示的场景作为验证测试。在图6中,所有车辆前面有另一辆车(黑色车辆4)以恒速行驶。自车仍然与V-A节相同,并由LFGC控制,这意味着从自车的角度来看,它正在与所有互动的车辆玩领导者-跟随者博弈。对于这三个相互作用的车辆(车辆1至3),它们由IDM控制,跟随前面车辆(车辆4)或具有一定时间前进t的自车。IDM模型参数列于表1。注意,自车将车辆4作为环境车辆,并假定其以恒速行驶。图6 当他车遵循IDM时,自车采用LFGC完成强制并道的场景示意图图7显示了自车与具有不同目标车辆和不同期望时间的IDM控制的他车进行交互时的结果。图7 :LFGC对IDM控制的不同目标和期望时间的他车的交互结果(a)车辆1产生(跟随自车)时间进展T = 1 [s],车辆2和车辆3跟随T = 0.5 [s];(b)车辆2产生(跟随自车)T=0.5[s],车辆1和3跟随前车辆T = 0.5 [s];(c)所有车辆跟随前车辆与T = 0.5 [s];(d)所有车辆跟随前车辆与T = 1.5 [s]。左栏(a-1)到(d-1)显示了自车对他车在博弈中的领导者的信念。右列(a-2)到(d-2)显示了在这个强制合并过程中自我和他车行为的时间历史结果。具体来说,在右栏中,每个块的边界线颜色区分不同的车辆,块中的数字表示时间以秒为单位,每个块的颜色描述该时刻的车辆速度,蓝色虚线表示自车的轨迹。在图7(a)中,第一辆交互车辆(车辆1)打算向自车让步,因此它选择跟随1秒时间前进的自车,而最后两辆交互车辆跟随0.5秒时间前进的前方车辆。从图7(a-1)中可以看出,自车认为车辆1有很高的概率成为博弈中的跟随者,并选择在车辆1的前面合并,如图7(a-2)所示。图7(b)显示了另一种情况,即第一辆交互车辆(车辆1)前进0.5,第二辆交互车辆打算向自车让步,前进0.5跟随自车。那么在这种情况下,从自车的角度来看,车辆1在博弈中成为领导者的概率更高,而车辆2在博弈中成为跟随者的概率更高,因此在这种情况下,自车在车辆2的前面成功合并。另外两个非产量情况如图7(c)和(d).所示图7(c)显示了跟随前面车辆的所有交互车辆的结果。从自车的角度来看,所有互动的车辆都更有可能成为博弈中的领导者,所以自车在所有车辆通过后都能成功地融合。在图7(d)中,所有相互作用的车辆都以1.5秒的速度前进。在这种情况下,自车发现车辆2的行为是保守的,并认为车辆2在博弈中成为跟随者的可能性更高。因此,自车成功地在车辆1和车辆2之间融合。在每个时间步长中,求解(22)的平均计算时间为0.198 [s]。我们已经在领导者-跟随者博弈中由领导者/跟随者驱动的他车和IDM模型上测试了LFGC。我们想用真实的流量数据来进一步测试控制器的性能。具体来说,我们使用了来自Next Generation Simulation(NGSIM)网站[34]的美国高速公路101交通数据集,该网站由美国联邦高速公路管理局收集,被认为是最大的公开的自然驾驶数据来源之一。美国高速公路101数据集已经在文献[44],[45],[46]中得到了广泛的研究。更具体地说,我们考虑了美国101交通数据集的一部分,其中包含了美国101高速公路上30分钟的车辆轨迹。时间段从早上7:50到8:20,这代表了上午高峰时间前后的拥堵。该数据集包含约6000辆车辆的位置和速度轨迹以及车辆尺寸,每0.1 [s]记录一次信息。用于收集数据的美国101高速公路部分的俯视图如图8所示。研究路段包括公路的五条主要车道,一条到公路的入口匝道,一条离开公路的出口匝道,以及一条用于并入公路和退出公路的辅助车道。正如在[47]中所讨论的,US101数据集由于视频分析和数值区分而包含了一个显著的噪声量。为了克服这一缺点,我们利用萨维茨基-戈雷滤波器[48]来平滑车辆的位置,并更新其相应的速度。Savitzky-Golay滤波器在时间窗口长度为21 [45]的US101数据集方面表现良好。一个原始车辆轨迹和相应的平滑车辆轨迹如图9所示。图8 用于收集美国101交通数据[34]的高速公路俯视图该路段包括高速公路的五条主要车道,一条通往高速公路的入口匝道,一条退出高速公路的出口匝道,还有一条用于并入高速公路和退出高速公路的辅助车道。图9 使用萨维茨基-戈雷滤波器从美国101交通数据集平滑的车辆轨迹对于LFGC的验证测试,我们关注入口匝道和辅助车道,以识别所有合并车辆。在识别了合并车辆和相应的场景后,我们根据图10识别了相互作用的车辆。具体来说,我们将目标车道上第一辆在2秒时间内的第一辆视为第一辆交互车辆,并将连续的车辆视为第二和第三辆车辆。对于场景中出现的所有他车,自车将把它们视为环境车辆,并假设它们以恒速行驶。一个已确定的合并场景如图11所示。图10 互动车辆的选择:自车(蓝色车辆)以选择框(红色框)内的车辆为互动车辆选择框的前端在自车前2个时间进展。以选择框内目标车道上的第一车辆为第一交互车辆,以以下车辆为第二和第三交互车辆。对于高速公路上的所有他车,它们被视为环境车辆,并假定保持恒定的速度。图11 从美国101流量数据集中确定的一个合并场景在此场景中,车辆0(蓝色车辆)是合并车辆,我们让LFGC来控制车辆0。根据我们选择交互车辆的标准,选择车辆1(红色车辆)和车辆2(粉红色车辆)作为交互车辆,并将所有他车(黑色车辆)视为环境车辆,假设其以定速行驶。对于每个合并场景,我们不是让自车跟踪交通数据,而是使用LFGC来控制自车的行为和结果轨迹。对于所有他车,包括相互作用的车辆和环境车辆,它们遵循它们在美国101交通数据集中出现的相应轨迹。然后,LFGC需要估计互动车辆的意图,并控制自车进行适当的合并。请注意,在数据收集过程中,交互车辆和环境车辆可能会在实际交通过程中与合并车辆进行交互。由于1)LFGC可能会采取不同于人类操作的行为,因此互动车辆或环境车辆的行为对自车的行为没有反应。相反,它们的行为是由流量数据集预先决定的,因此需要采取保守的措施来避免碰撞;2)交通密集,使自车没有安全的边际合并而不与他车的碰撞箱相交。表2:使用US101流量数据集验证LFGC的统计数据”成功“意味着自车成功地合并到目标车道上,而没有任何碰撞。”失败合并”意味着自车不能在辅助车道的末端合并。“碰撞”是指自车与他车发生碰撞。最后,作者取一个并入过程的截图进行了分析。在图12中,我们展示了一个成功合并的屏幕截图。在这些图中,蓝色的车辆由LFGC控制,灰色的盒子表示自车在数据集中的实际位置。所有他车(包括红色的交互车辆和黑色的环境车辆)都在数据集中遵循它们相应的轨迹。由LFGC控制的自车与人类驾驶员(灰色盒子)做出类似的决定:LFGC和人类驾驶员首先都试图加速并在卡车前面合并(车辆1)。然而,在认识到卡车更有可能继续不屈服后,自车决定减速,并在卡车后合并。图12 在对美国高速公路101数据集验证LFGC时成功并道的说明其中蓝色车辆是由LFGC控制的自车,灰色框是数据中出现的自车的位置。在本文中,我们提出了一种用于合并场景中自动车辆规划和控制的领跟随博弈控制器(LFGC)。LFGC将不同驾驶员意图导致的交互不确定性作为潜在变量,估计其他驾驶员意图,并选择促进自车合并的行动。特别是,LFGC能够执行一个明确的概率安全特性,即受到车辆安全约束。通过考虑自车和交互车辆的两两交互,LFGC能够以一种可计算处理的方式处理与多辆车辆的交互。最后,进行了多个基于模拟的验证,以证明LFGC的有效性,包括他车在博弈中关注领导者或跟随者的场景,智能驾驶员模型(IDM),以及实际的美国高速公路101数据。《Interaction-Aware Trajectory Prediction and Planning for Autonomous Vehicles in Forced Merge Scenarios》IEEE Transactions on Intelligent Transportation SystemsKaiwen Liu, Nan Li, H. Eric Tseng, Ilya Kolmanovsky, and Anouck Girardhttps://arxiv.org/abs/2112.07624v1https://ieeexplore.ieee.org/abstract/document/9936045
的最小车辆、期望的时间T和舒适减速度b。我们考虑了图6中所示的场景作为验证测试。在图6中,所有车辆前面有另一辆车(黑色车辆4)以恒速行驶。自车仍然与V-A节相同,并由LFGC控制,这意味着从自车的角度来看,它正在与所有互动的车辆玩领导者-跟随者博弈。对于这三个相互作用的车辆(车辆1至3),它们由IDM控制,跟随前面车辆(车辆4)或具有一定时间前进t的自车。IDM模型参数列于表1。注意,自车将车辆4作为环境车辆,并假定其以恒速行驶。图6 当他车遵循IDM时,自车采用LFGC完成强制并道的场景示意图图7显示了自车与具有不同目标车辆和不同期望时间的IDM控制的他车进行交互时的结果。图7 :LFGC对IDM控制的不同目标和期望时间的他车的交互结果(a)车辆1产生(跟随自车)时间进展T = 1 [s],车辆2和车辆3跟随T = 0.5 [s];(b)车辆2产生(跟随自车)T=0.5[s],车辆1和3跟随前车辆T = 0.5 [s];(c)所有车辆跟随前车辆与T = 0.5 [s];(d)所有车辆跟随前车辆与T = 1.5 [s]。左栏(a-1)到(d-1)显示了自车对他车在博弈中的领导者的信念。右列(a-2)到(d-2)显示了在这个强制合并过程中自我和他车行为的时间历史结果。具体来说,在右栏中,每个块的边界线颜色区分不同的车辆,块中的数字表示时间以秒为单位,每个块的颜色描述该时刻的车辆速度,蓝色虚线表示自车的轨迹。在图7(a)中,第一辆交互车辆(车辆1)打算向自车让步,因此它选择跟随1秒时间前进的自车,而最后两辆交互车辆跟随0.5秒时间前进的前方车辆。从图7(a-1)中可以看出,自车认为车辆1有很高的概率成为博弈中的跟随者,并选择在车辆1的前面合并,如图7(a-2)所示。图7(b)显示了另一种情况,即第一辆交互车辆(车辆1)前进0.5,第二辆交互车辆打算向自车让步,前进0.5跟随自车。那么在这种情况下,从自车的角度来看,车辆1在博弈中成为领导者的概率更高,而车辆2在博弈中成为跟随者的概率更高,因此在这种情况下,自车在车辆2的前面成功合并。另外两个非产量情况如图7(c)和(d).所示图7(c)显示了跟随前面车辆的所有交互车辆的结果。从自车的角度来看,所有互动的车辆都更有可能成为博弈中的领导者,所以自车在所有车辆通过后都能成功地融合。在图7(d)中,所有相互作用的车辆都以1.5秒的速度前进。在这种情况下,自车发现车辆2的行为是保守的,并认为车辆2在博弈中成为跟随者的可能性更高。因此,自车成功地在车辆1和车辆2之间融合。在每个时间步长中,求解(22)的平均计算时间为0.198 [s]。我们已经在领导者-跟随者博弈中由领导者/跟随者驱动的他车和IDM模型上测试了LFGC。我们想用真实的流量数据来进一步测试控制器的性能。具体来说,我们使用了来自Next Generation Simulation(NGSIM)网站[34]的美国高速公路101交通数据集,该网站由美国联邦高速公路管理局收集,被认为是最大的公开的自然驾驶数据来源之一。美国高速公路101数据集已经在文献[44],[45],[46]中得到了广泛的研究。更具体地说,我们考虑了美国101交通数据集的一部分,其中包含了美国101高速公路上30分钟的车辆轨迹。时间段从早上7:50到8:20,这代表了上午高峰时间前后的拥堵。该数据集包含约6000辆车辆的位置和速度轨迹以及车辆尺寸,每0.1 [s]记录一次信息。用于收集数据的美国101高速公路部分的俯视图如图8所示。研究路段包括公路的五条主要车道,一条到公路的入口匝道,一条离开公路的出口匝道,以及一条用于并入公路和退出公路的辅助车道。正如在[47]中所讨论的,US101数据集由于视频分析和数值区分而包含了一个显著的噪声量。为了克服这一缺点,我们利用萨维茨基-戈雷滤波器[48]来平滑车辆的位置,并更新其相应的速度。Savitzky-Golay滤波器在时间窗口长度为21 [45]的US101数据集方面表现良好。一个原始车辆轨迹和相应的平滑车辆轨迹如图9所示。图8 用于收集美国101交通数据[34]的高速公路俯视图该路段包括高速公路的五条主要车道,一条通往高速公路的入口匝道,一条退出高速公路的出口匝道,还有一条用于并入高速公路和退出高速公路的辅助车道。图9 使用萨维茨基-戈雷滤波器从美国101交通数据集平滑的车辆轨迹对于LFGC的验证测试,我们关注入口匝道和辅助车道,以识别所有合并车辆。在识别了合并车辆和相应的场景后,我们根据图10识别了相互作用的车辆。具体来说,我们将目标车道上第一辆在2秒时间内的第一辆视为第一辆交互车辆,并将连续的车辆视为第二和第三辆车辆。对于场景中出现的所有他车,自车将把它们视为环境车辆,并假设它们以恒速行驶。一个已确定的合并场景如图11所示。图10 互动车辆的选择:自车(蓝色车辆)以选择框(红色框)内的车辆为互动车辆选择框的前端在自车前2个时间进展。以选择框内目标车道上的第一车辆为第一交互车辆,以以下车辆为第二和第三交互车辆。对于高速公路上的所有他车,它们被视为环境车辆,并假定保持恒定的速度。图11 从美国101流量数据集中确定的一个合并场景在此场景中,车辆0(蓝色车辆)是合并车辆,我们让LFGC来控制车辆0。根据我们选择交互车辆的标准,选择车辆1(红色车辆)和车辆2(粉红色车辆)作为交互车辆,并将所有他车(黑色车辆)视为环境车辆,假设其以定速行驶。对于每个合并场景,我们不是让自车跟踪交通数据,而是使用LFGC来控制自车的行为和结果轨迹。对于所有他车,包括相互作用的车辆和环境车辆,它们遵循它们在美国101交通数据集中出现的相应轨迹。然后,LFGC需要估计互动车辆的意图,并控制自车进行适当的合并。请注意,在数据收集过程中,交互车辆和环境车辆可能会在实际交通过程中与合并车辆进行交互。由于1)LFGC可能会采取不同于人类操作的行为,因此互动车辆或环境车辆的行为对自车的行为没有反应。相反,它们的行为是由流量数据集预先决定的,因此需要采取保守的措施来避免碰撞;2)交通密集,使自车没有安全的边际合并而不与他车的碰撞箱相交。表2:使用US101流量数据集验证LFGC的统计数据”成功“意味着自车成功地合并到目标车道上,而没有任何碰撞。”失败合并”意味着自车不能在辅助车道的末端合并。“碰撞”是指自车与他车发生碰撞。最后,作者取一个并入过程的截图进行了分析。在图12中,我们展示了一个成功合并的屏幕截图。在这些图中,蓝色的车辆由LFGC控制,灰色的盒子表示自车在数据集中的实际位置。所有他车(包括红色的交互车辆和黑色的环境车辆)都在数据集中遵循它们相应的轨迹。由LFGC控制的自车与人类驾驶员(灰色盒子)做出类似的决定:LFGC和人类驾驶员首先都试图加速并在卡车前面合并(车辆1)。然而,在认识到卡车更有可能继续不屈服后,自车决定减速,并在卡车后合并。图12 在对美国高速公路101数据集验证LFGC时成功并道的说明其中蓝色车辆是由LFGC控制的自车,灰色框是数据中出现的自车的位置。在本文中,我们提出了一种用于合并场景中自动车辆规划和控制的领跟随博弈控制器(LFGC)。LFGC将不同驾驶员意图导致的交互不确定性作为潜在变量,估计其他驾驶员意图,并选择促进自车合并的行动。特别是,LFGC能够执行一个明确的概率安全特性,即受到车辆安全约束。通过考虑自车和交互车辆的两两交互,LFGC能够以一种可计算处理的方式处理与多辆车辆的交互。最后,进行了多个基于模拟的验证,以证明LFGC的有效性,包括他车在博弈中关注领导者或跟随者的场景,智能驾驶员模型(IDM),以及实际的美国高速公路101数据。《Interaction-Aware Trajectory Prediction and Planning for Autonomous Vehicles in Forced Merge Scenarios》IEEE Transactions on Intelligent Transportation SystemsKaiwen Liu, Nan Li, H. Eric Tseng, Ilya Kolmanovsky, and Anouck Girardhttps://arxiv.org/abs/2112.07624v1https://ieeexplore.ieee.org/abstract/document/9936045参考文献
转载自网络,文中观点仅供分享交流,不代表本公众号立场,如涉及版权等问题,请您告知,我们将及时处理。
-- END --
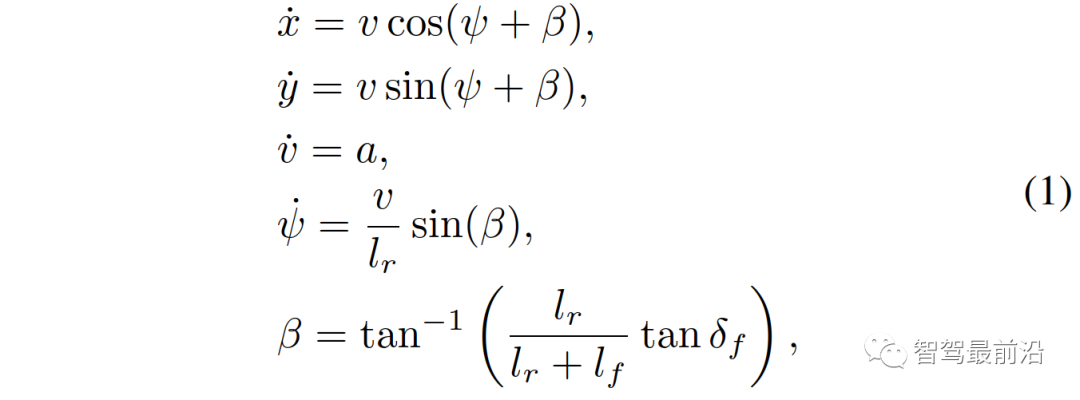
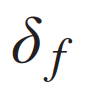 ,没有后轮转向(即
,没有后轮转向(即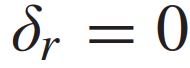 );x、y是车辆的纵向、横向位置;v是车辆的速度;ψ和β是车辆的偏航角和滑移角;
);x、y是车辆的纵向、横向位置;v是车辆的速度;ψ和β是车辆的偏航角和滑移角;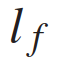 和
和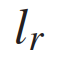 表示车辆从CG到前轮和后轮轴的距离;a是沿速度v方向的加速度。控制输入是加速和前轮转向,
表示车辆从CG到前轮和后轮轴的距离;a是沿速度v方向的加速度。控制输入是加速和前轮转向,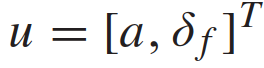 。
。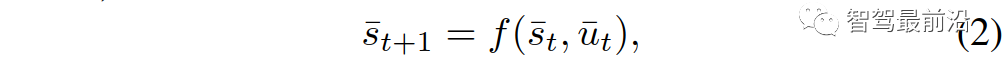
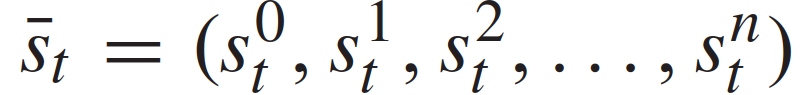 表示离散时刻的n+1量车的交通状态,
表示离散时刻的n+1量车的交通状态,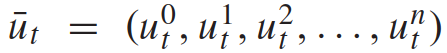 表示时间t时所有n + 1辆车辆的控制输入的集合。每辆车的状态
表示时间t时所有n + 1辆车辆的控制输入的集合。每辆车的状态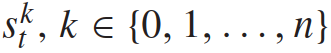 包括它的xy坐标、速度和偏航角;控制输入
包括它的xy坐标、速度和偏航角;控制输入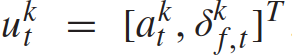 。
。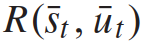 是驾驶员驾驶目标的数学表示,交通状态是由这两辆车的状态组成的,而自车获得的奖励取决于两交互车的状态和控制输入。我们考虑
是驾驶员驾驶目标的数学表示,交通状态是由这两辆车的状态组成的,而自车获得的奖励取决于两交互车的状态和控制输入。我们考虑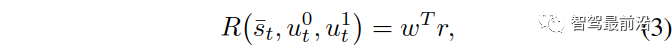
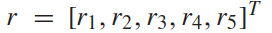 ,
,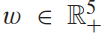 是一个权重向量。奖励项
是一个权重向量。奖励项 代表驾驶过程中的以下常见考虑:1)安全性
代表驾驶过程中的以下常见考虑:1)安全性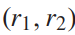 ,即不与他车相撞、不离开道路;2)并道意愿
,即不与他车相撞、不离开道路;2)并道意愿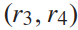 ,即与目的车道的距离;3)舒适性
,即与目的车道的距离;3)舒适性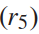 ,即与他车保持合理的间距。
,即与他车保持合理的间距。 的更定义详见[33]。
的更定义详见[33]。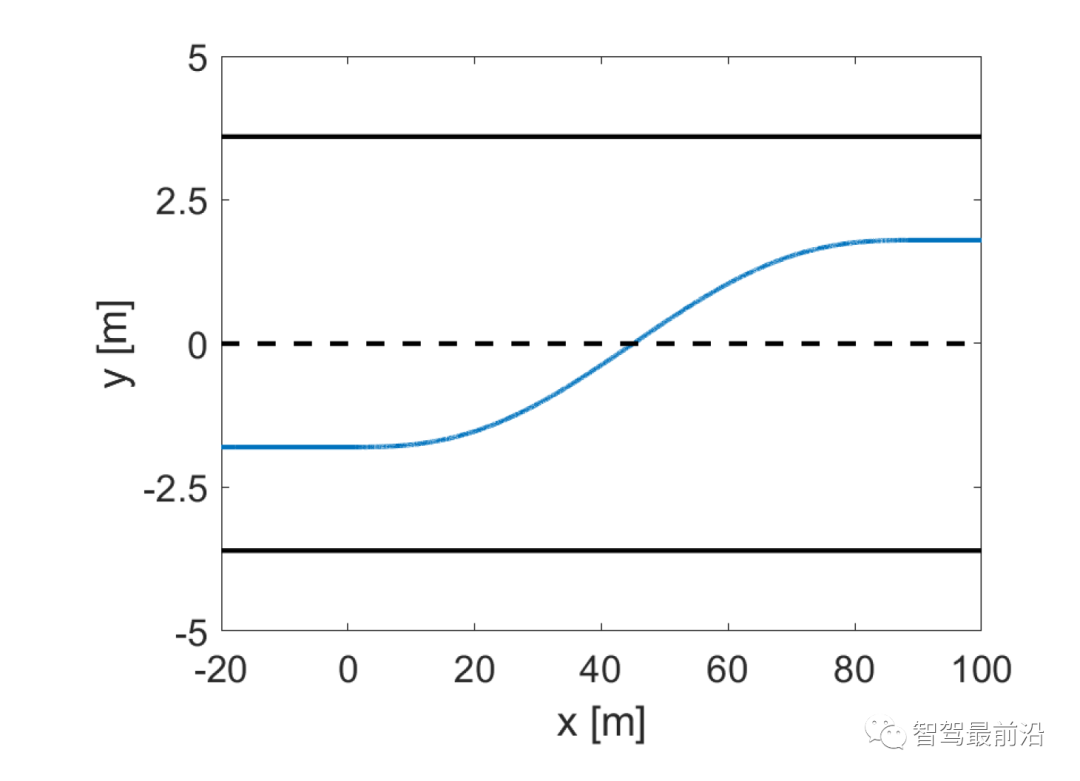
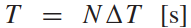 上的车辆运动轨迹样本作为每个车辆的动作空间。具体来说,每个轨迹都是从车辆当前状态
上的车辆运动轨迹样本作为每个车辆的动作空间。具体来说,每个轨迹都是从车辆当前状态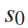 开始的车辆状态
开始的车辆状态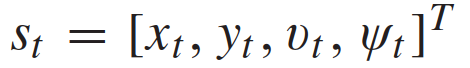 的时间历史。
的时间历史。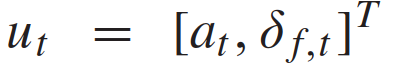 计算出来。
计算出来。 和
和 ,这些车辆的运动学模型(1)简化为:
,这些车辆的运动学模型(1)简化为: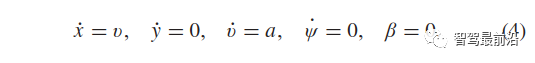
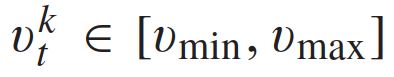 。
。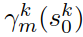 ,m = 1,2,……81,轨迹的集合记为
,m = 1,2,……81,轨迹的集合记为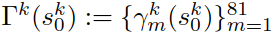
 和
和 ,使5阶多项式
,使5阶多项式
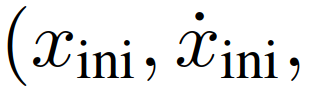
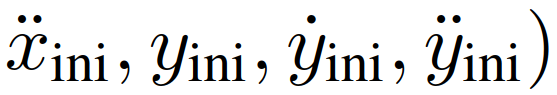 和终值条件
和终值条件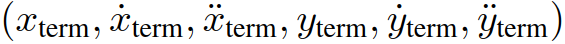 。(5)中的变量ζ表示连续时间,当前样本的ζ=0。
。(5)中的变量ζ表示连续时间,当前样本的ζ=0。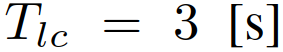 为常数[37]。允许车辆在变道过程随时终止变道行为,这代表当先前计划的变道变得不可行/安全时,司机“改变主意”。中止变道后的轨迹通过类似变道轨迹的方式生成。
为常数[37]。允许车辆在变道过程随时终止变道行为,这代表当先前计划的变道变得不可行/安全时,司机“改变主意”。中止变道后的轨迹通过类似变道轨迹的方式生成。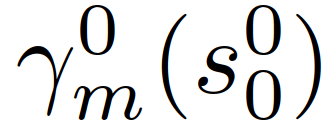 ,m = 1,2,……,162;轨迹集合为
,m = 1,2,……,162;轨迹集合为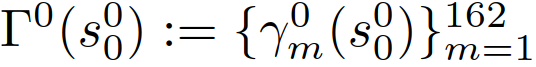 。
。
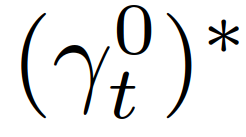 ,根据在规划范围内最大化其累积奖励:
,根据在规划范围内最大化其累积奖励:
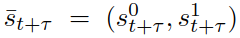 表示离散时刻t+τ的预测交通状态,而
表示离散时刻t+τ的预测交通状态,而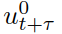 和
和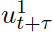 分别表示预测的自车和交互车辆在t+τ的控制输入。参数λ∈(0,1)是未来奖励的损益系数,即优先考虑当下的奖励。在(6)中,
分别表示预测的自车和交互车辆在t+τ的控制输入。参数λ∈(0,1)是未来奖励的损益系数,即优先考虑当下的奖励。在(6)中,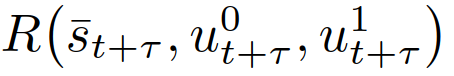 代表自车在t+τ时的奖励,如第II-C节所述,
代表自车在t+τ时的奖励,如第II-C节所述, 代表一组交通状态的安全值,用于执行严格的安全规范(如防碰撞、道路边界约束等)。在获得最优轨迹
代表一组交通状态的安全值,用于执行严格的安全规范(如防碰撞、道路边界约束等)。在获得最优轨迹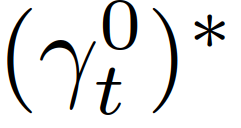 后,自车用与该轨迹对应的控制输入
后,自车用与该轨迹对应的控制输入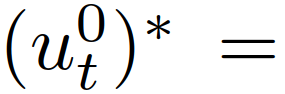
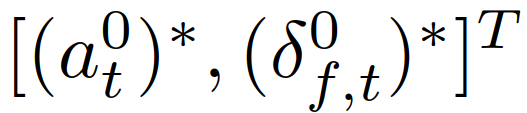 ,在一个采样周期内更新其状态,然后在下一个采样时间瞬间t + 1重复上述步骤。
,在一个采样周期内更新其状态,然后在下一个采样时间瞬间t + 1重复上述步骤。
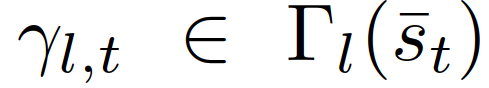 和
和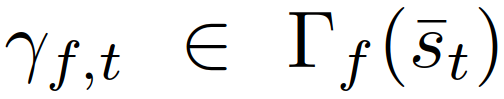 ,其中
,其中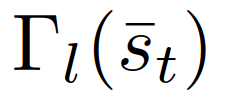 和
和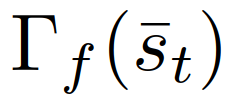 为领导者、跟随者的可行轨迹集。假设博弈双方都做出了最大化其累积奖励的决定,分别记为
为领导者、跟随者的可行轨迹集。假设博弈双方都做出了最大化其累积奖励的决定,分别记为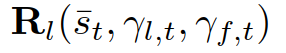 和
和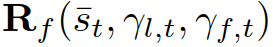 ,定义如下:
,定义如下: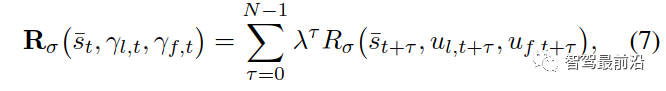
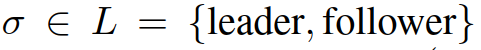 代表博弈中的角色,
代表博弈中的角色,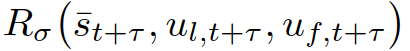 是领导者/跟随者的奖励函数,
是领导者/跟随者的奖励函数, 和
和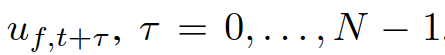 表示对应二者轨迹
表示对应二者轨迹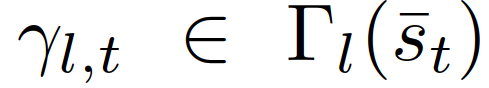 和
和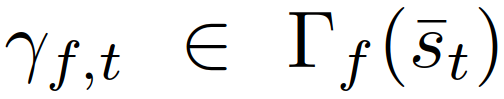 的控制输入量。
的控制输入量。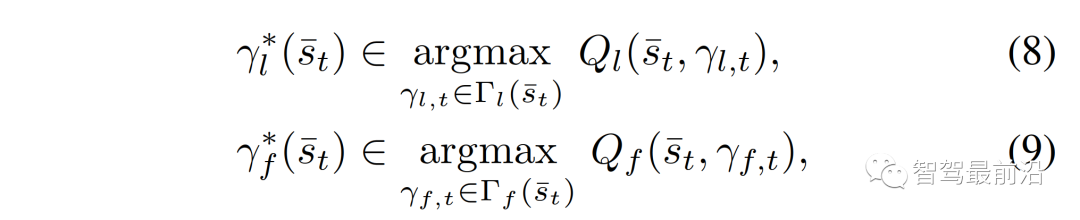
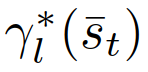 (区别于
(区别于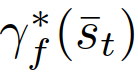 )是领导者(区别于跟随者)的最优轨迹,取决于当前交通状态,
)是领导者(区别于跟随者)的最优轨迹,取决于当前交通状态,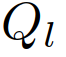 和
和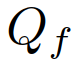 定义如下:
定义如下: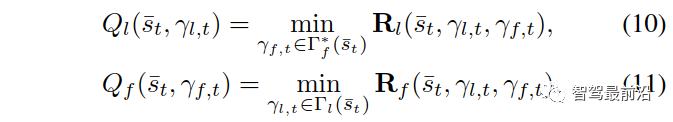
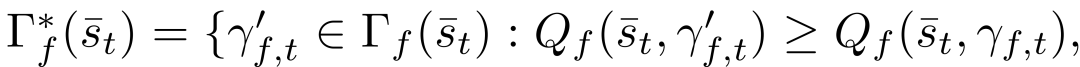
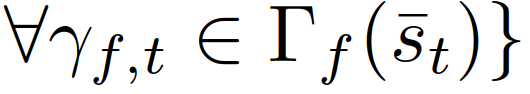 。
。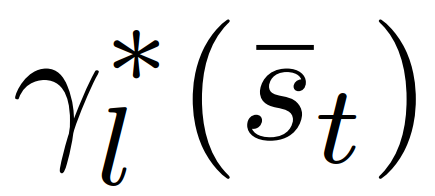 、跟随者的最优行动策略
、跟随者的最优行动策略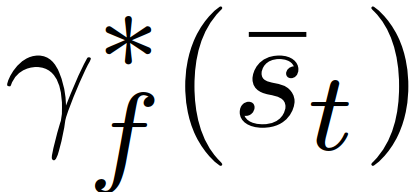 都可通过(8)-(11)获得。但 (8)-(11)的重复在线计算会很耗时。因此,我们将使用模仿学习显式地表示
都可通过(8)-(11)获得。但 (8)-(11)的重复在线计算会很耗时。因此,我们将使用模仿学习显式地表示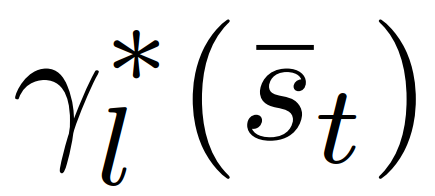 和
和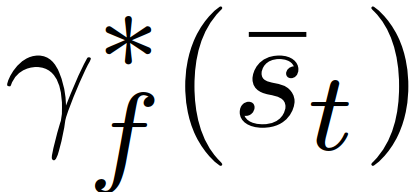 。
。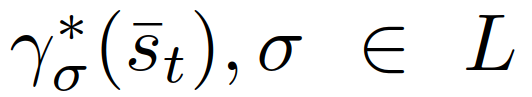 。
。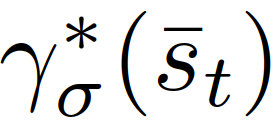 。
。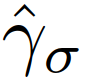 。
。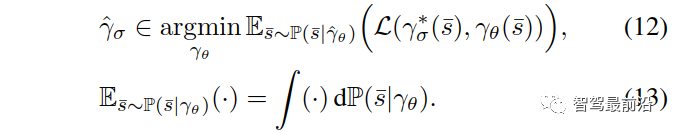
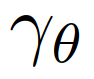 表示使用θ(神经网络权重)参数化的策略,
表示使用θ(神经网络权重)参数化的策略,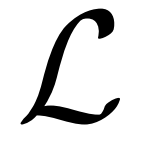 表示损失函数,关于模仿学习和“数据集聚合”算法详见[39]和[40]。
表示损失函数,关于模仿学习和“数据集聚合”算法详见[39]和[40]。
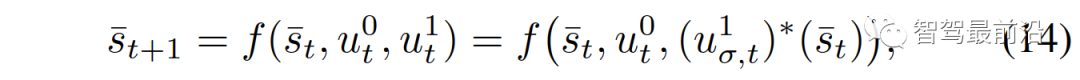
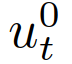 是自车的控制,
是自车的控制,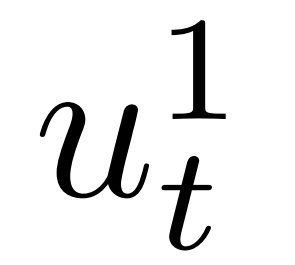 是交互车辆的控制,由领导者跟随者博弈得到,
是交互车辆的控制,由领导者跟随者博弈得到,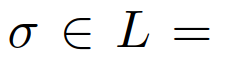 {领导者,跟随者}代表跟随者或领导者,并且
{领导者,跟随者}代表跟随者或领导者,并且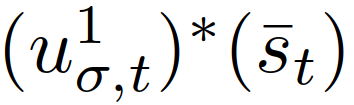 第一个控制输入,对应(8)(9)中
第一个控制输入,对应(8)(9)中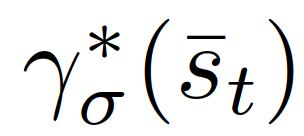 的最优轨迹。现在(14)的唯一输入是对自车的控制
的最优轨迹。现在(14)的唯一输入是对自车的控制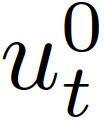 。
。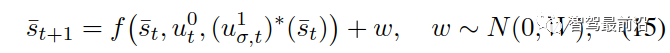
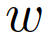 为均值和协方差为0的加性高斯噪声。
为均值和协方差为0的加性高斯噪声。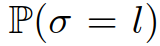 ,其中
,其中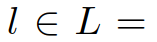 {领导者,跟随者}。然后根据所有以前的交通状态和自车所采取的所有行动
{领导者,跟随者}。然后根据所有以前的交通状态和自车所采取的所有行动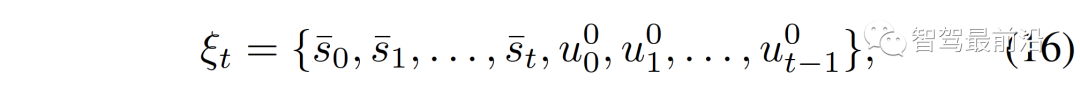
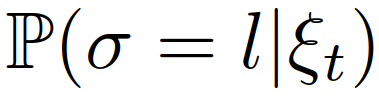 。
。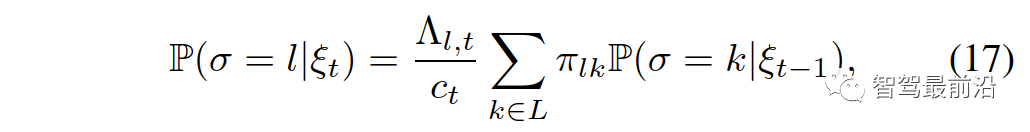
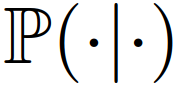 为条件概率;
为条件概率;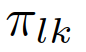 为作用车角色从
为作用车角色从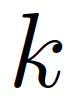 到
到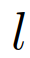 的转移概率;
的转移概率;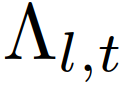 为作用车角色
为作用车角色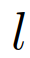 的似然函数,定义为:
的似然函数,定义为: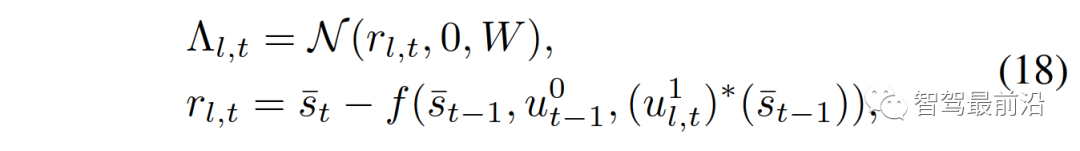
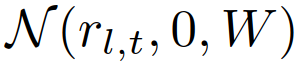 为正态分布的概率密度函数,均值为0,协方差W在
为正态分布的概率密度函数,均值为0,协方差W在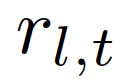 评估;
评估;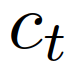 为归一化常数。
为归一化常数。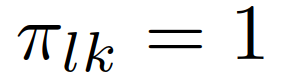 时
时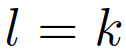 ,当
,当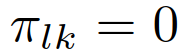 时,交互车辆的领导者或跟随者角色的后验信念可以使用以下方程更新:
时,交互车辆的领导者或跟随者角色的后验信念可以使用以下方程更新: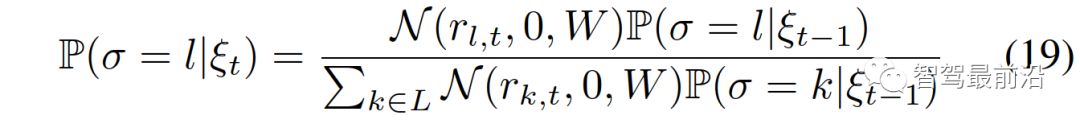
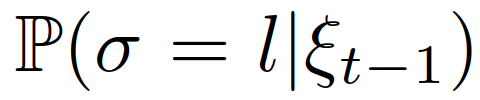 是交互车辆的领导者或跟随者的角色的先验信念。
是交互车辆的领导者或跟随者的角色的先验信念。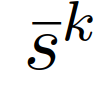 ,
,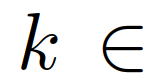
 ,每个的动态模型由下式给出:
,每个的动态模型由下式给出: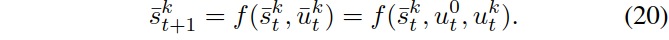
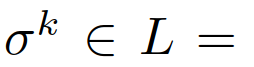 {领导者,跟随者}表示第k个交互车辆的成对领导者或跟随者角色,用
{领导者,跟随者}表示第k个交互车辆的成对领导者或跟随者角色,用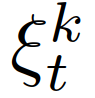 表示自车所有之前的成对交通状态和行动的集合,即,
表示自车所有之前的成对交通状态和行动的集合,即,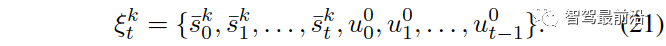
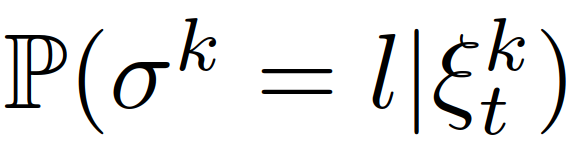 ,
,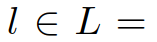 {领导者,跟随者}。(6)中基于MPC的控制策略可以重新表述为:
{领导者,跟随者}。(6)中基于MPC的控制策略可以重新表述为: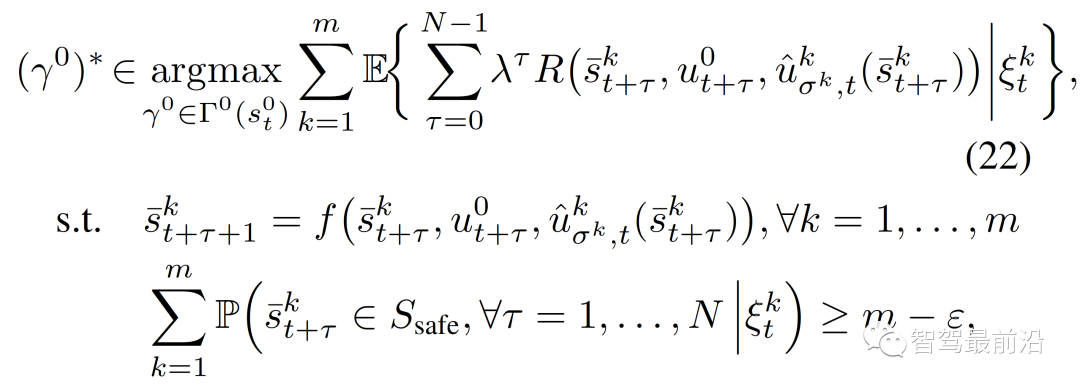
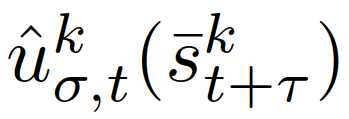 是(12)中训练策略
是(12)中训练策略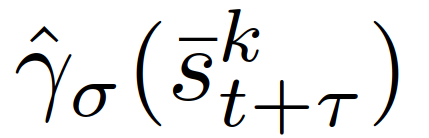 的轨迹对应的第一个控制输入,ε∈[0,1]表示(用户指定的)所需的约束满足概率水平。
的轨迹对应的第一个控制输入,ε∈[0,1]表示(用户指定的)所需的约束满足概率水平。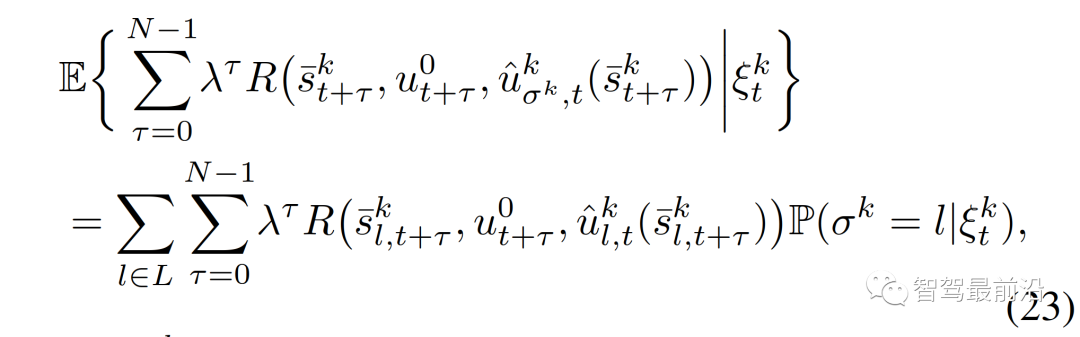
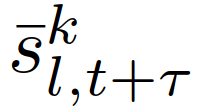 为给定交互车辆的角色为
为给定交互车辆的角色为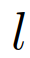 的预测交通状态,
的预测交通状态,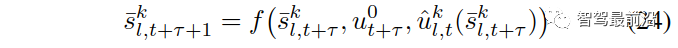
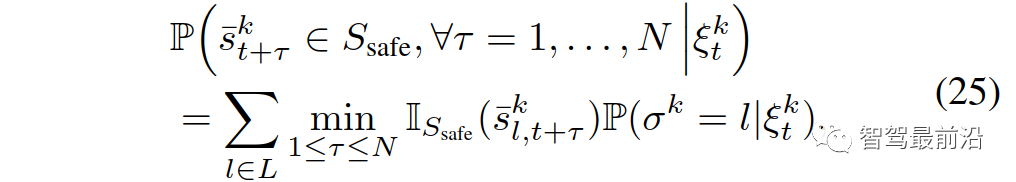
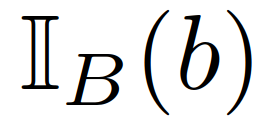 为集合B中b的指示器函数。
为集合B中b的指示器函数。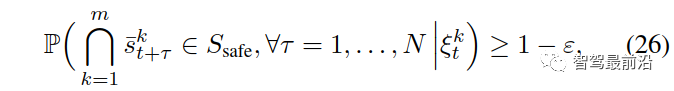
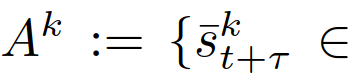
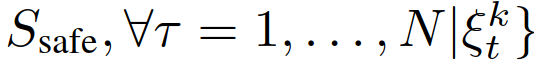 然后
然后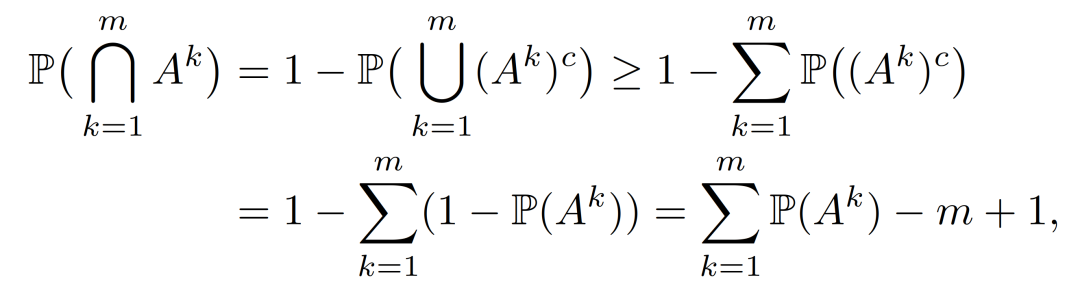
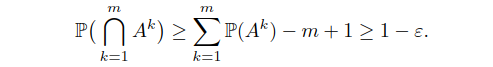
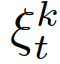 中。对每辆车的领导者或跟随者角色的信念根据(19)进行更新。然后,利用基于MPC的控制策略(22),通过搜索第2-D节中引入的所有轨迹,得到最优轨迹
中。对每辆车的领导者或跟随者角色的信念根据(19)进行更新。然后,利用基于MPC的控制策略(22),通过搜索第2-D节中引入的所有轨迹,得到最优轨迹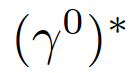 ,自车在一个采样周期内应用第一个控制输入来更新其状态。整个过程将在下一次采样时重复进行。
,自车在一个采样周期内应用第一个控制输入来更新其状态。整个过程将在下一次采样时重复进行。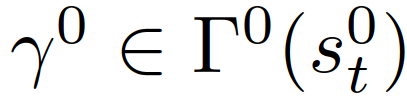 ,他车特定意图下的轨迹预测也是不同的。这种情况是因为预测的他车的行为依赖于交通状态,而预测的交通状态依赖于自车的规划轨迹。
,他车特定意图下的轨迹预测也是不同的。这种情况是因为预测的他车的行为依赖于交通状态,而预测的交通状态依赖于自车的规划轨迹。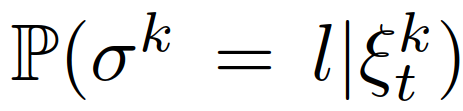 。同时,根据他车之前的交互行为来估计他车意图。
。同时,根据他车之前的交互行为来估计他车意图。
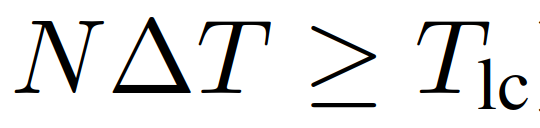 )。
)。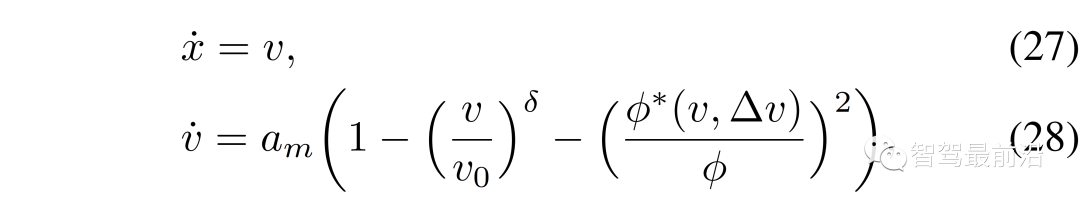
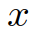 为纵向位置;
为纵向位置;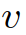 为纵向速度;
为纵向速度;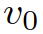 为车辆的期望速度;
为车辆的期望速度;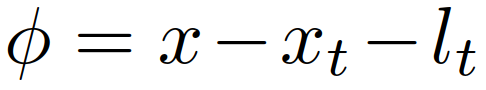 为跟车距离,
为跟车距离,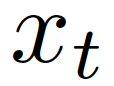 为目标车辆的位置,
为目标车辆的位置,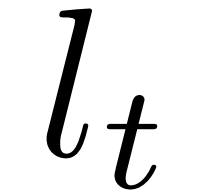 为目标车辆的长度;
为目标车辆的长度;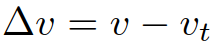 是车辆与目标车辆的速度差;
是车辆与目标车辆的速度差;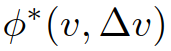 根据:
根据: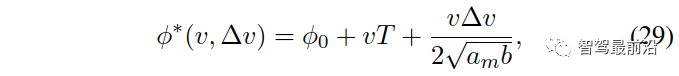
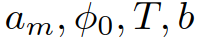 为IDM模型的参数。这些参数的物理解释是最大加速度
为IDM模型的参数。这些参数的物理解释是最大加速度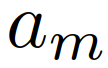 、跟随距离
、跟随距离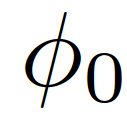 的最小车辆、期望的时间T和舒适减速度b。
的最小车辆、期望的时间T和舒适减速度b。