扬声器震动的频率特性可以通过敲击它所获得的冲激响应来分析。 原本驱动扬声器纸盆震动的线圈此时可以用作震动传感器, 它将纸盆的震动速度转换成电压信号。 通过示波器可以采集到这个信号, 本文将对敲击扬声器所产生的震动信号进行观察建模。

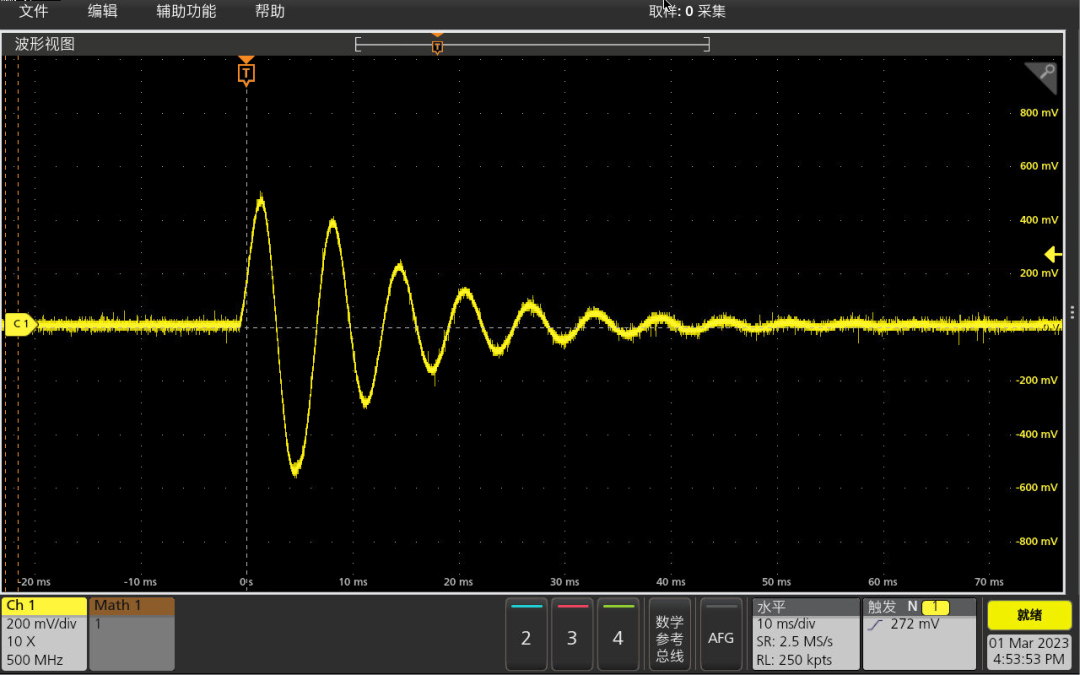
使用示波器连接扬声器的引线, 敲击扬声器可以看到振动的波形。 不同的敲击力度和部位, 对应的震动还是有些区别。 示波器的探头直接连接到扬声器的音圈输出端口, 中间没有施加任何信号放大电路。 这样采集到的电压信号反映了扬声器的单位冲激响应。

为了便于分析,使用小型改锥敲击扬声器纸盆中心,获得了这样一个简单衰减振荡波形。 选择其中三个周期过零点, 查看它们之间的时间差, 大约为19.5毫秒, 它的倒数对应51.3Hz。 由于这是三个振荡周期,所以原波形的振荡频率为153.9Hz。
为了进一步精确估计衰减振荡波形参数, 通过Python编程,从示波器读取波形数据。 这是对读取数据显示的波形。 对原始示波器采集到的数据进行50个数据点的平均, 获得更加光滑的信号波形。
#!/usr/local/bin/python
# -*- coding: gbk -*-
#******************************
# TEST1.PY -- by Dr. ZhuoQing 2023-03-01
#
# Note:
#******************************
from headm import *
from tsmodule.tsvisa import *
mso24open()
x,y = mso24read(1)
tspsave('wave1', x=x, y=y)
plt.plot(x, y)
plt.xlabel("Time(s)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
# END OF FILE : TEST1.PY
#******************************
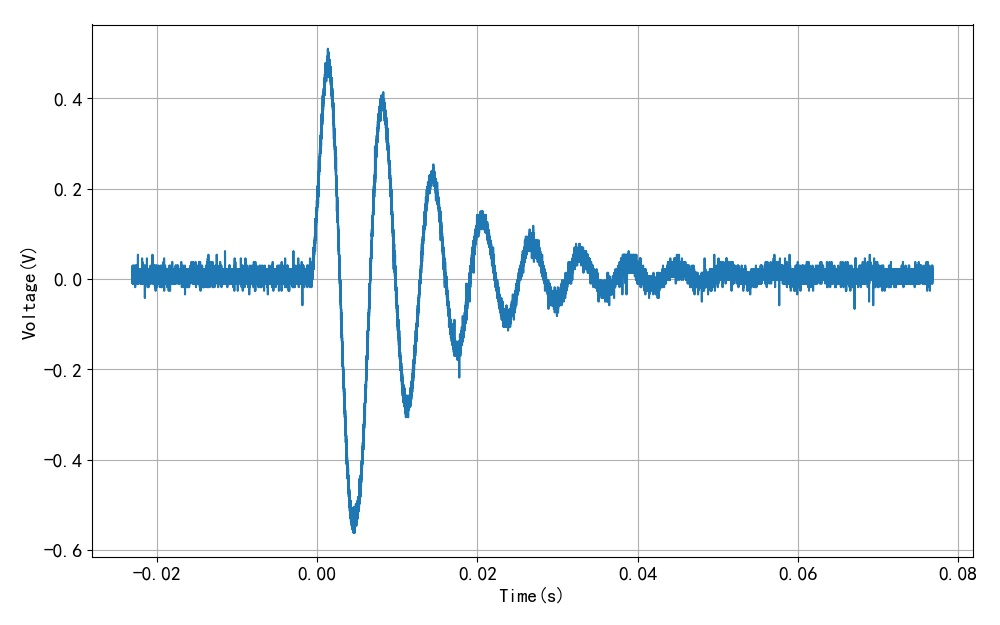
▲ 图1.2.1 敲击扬声器中间获得的波形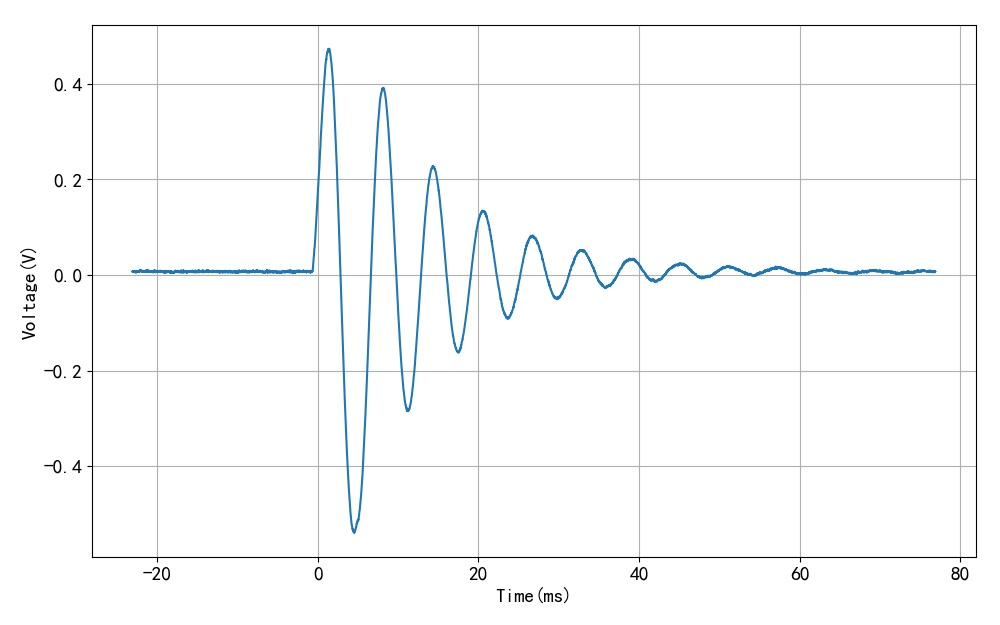
▲ 图1.2.2 50个数据进行平滑之后的波形下面通过曲线拟合方式对扬声器振动信号进行建模。 由于信号前面的波形受到敲击的影响, 所以并不纯粹是扬声器自由响应。 截取时间大于7毫秒之后的波形进行处理。 这是扬声器在敲击后7毫秒之后的震动信号波形。 它是一个指数衰减振荡信号。 可以使用一个带有五个参数的函数表示。 通过Python编程, 利用其中的曲线拟合工具来估计波形参数。
下面是程序拟合过程。 定义带有五个参数的指数衰减函数, 根据观察到的波形,初步估计函数的五个参数的初始值,调用曲线拟合函数, 显示获得拟合参数。 利用这些参数计算出拟合曲线,并进行绘制。 下面分析一下拟合结果。 这是五个信号参数拟合数值, 其中参数C代表着振荡角频率。 通过它, 可以计算出振荡频率 f0。 f0 等于 161.2 赫兹。
这里将原始波形和拟合曲线波形绘制在一起, 可以看到拟合参数的有效性。 利用测量波形进行曲线拟合,所获得的频率值应该比前面观察到曲线过零点所获得频率更加准确。
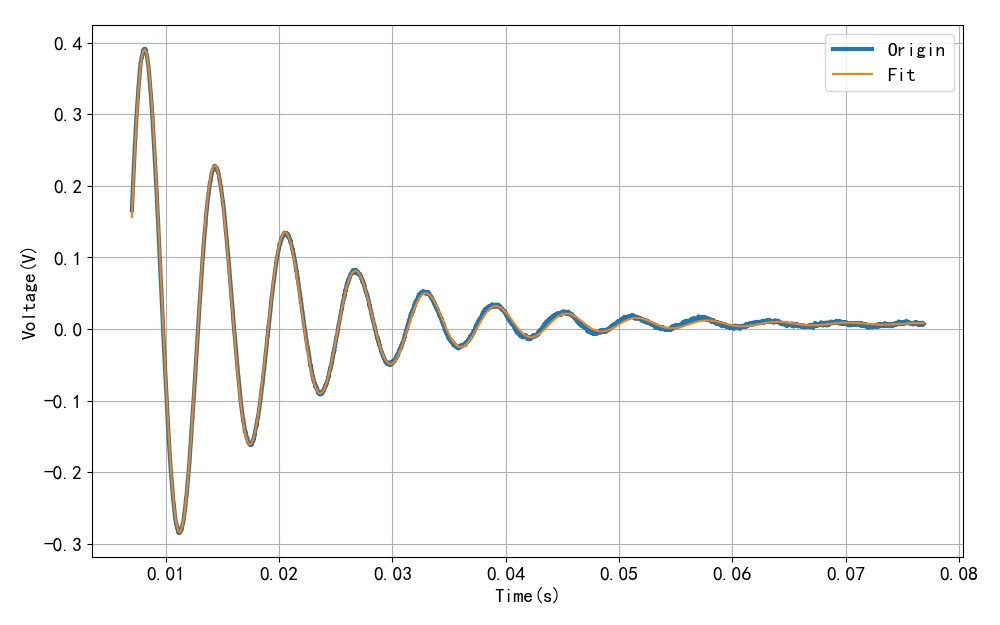
▲ 图1.2.3 曲线拟合后的结果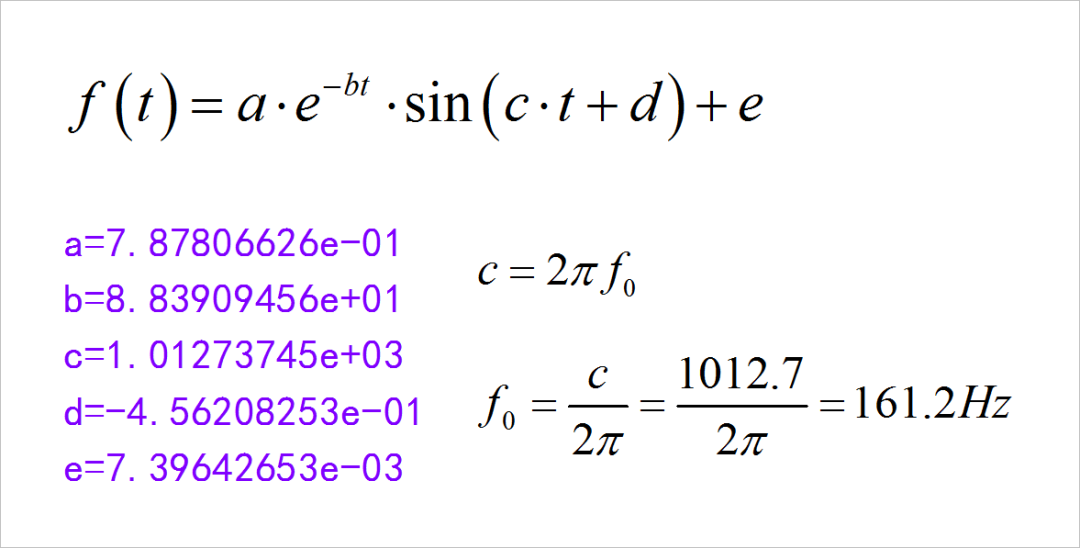
▲ 图1.3.2 信号波形拟合函数以及对应的参数#!/usr/local/bin/python
# -*- coding: gbk -*-
#******************************
# TEST2.PY -- by Dr. ZhuoQing 2023-03-01
#
# Note:
#******************************
from headm import *
from scipy.optimize import curve_fit
x, y = tspload('wave1', 'x', 'y')
printf(len(x), len(y))
AVERAGE_NUM = 50
DATA_LENGTH = len(x)//AVERAGE_NUM
xx = array([sum(x[i*AVERAGE_NUM:i*AVERAGE_NUM+AVERAGE_NUM])/AVERAGE_NUM*1e3 for i in range(DATA_LENGTH)])
yy = array([sum(y[i*AVERAGE_NUM:i*AVERAGE_NUM+AVERAGE_NUM])/AVERAGE_NUM for i in range(DATA_LENGTH)])
c = where(xx>5)
xxx = xx[c]/1000
yyy = yy[c]
tspsave('wave11', xxx=xxx, yyy=yyy)
#------------------------------------------------------------
'''
plt.plot(xxx, yyy)
plt.xlabel("Time(s)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.tight_layout()
plt.show()
'''
#------------------------------------------------------------
def fun(x,a,b,c,d,e):
return a*exp(-b*x)*sin(c*x+d)+e
param = (1, 50, 2*pi*150, 0, 0)
param, conv = curve_fit(fun, xxx, yyy, p0=param)
printf(param)
ysim = fun(xxx, *param)
plt.plot(xxx, yyy, linewidth=3, label='Origin')
plt.plot(xxx, ysim, label='Fit')
plt.xlabel("Time(s)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()
#------------------------------------------------------------
# END OF FILE : TEST2.PY
#******************************
下面是文件 headm.py 的内容:
import sys, os
sys.path.append(r'd:\python\teasoft')
STDFILE = open(r'd:\python\std.txt', 'a', 1)
sysstderr = sys.stderr
sysstdout = sys.stdout
sys.stderr = STDFILE
sys.stdout = STDFILE
from threading import Thread
import time, math, winsound, clipboard, random
from numpy import *
from tsmodule.tspdata import *
from tsmodule.tspyt import *
from tsmodule.tscmd import *
from tsmodule.tsdopop import *
from tsmodule.tsdraw import *
import tsmodule.tsconfig
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,80*10/128))
plt.get_current_fig_manager().window.wm_geometry("+1950+300")
plt.rcParams.update({'font.size':14})
本文通过示波器观察并获取了一种小型扬声器敲击信号。该信号反映了扬声器的冲激响应。 后面通过信号拟合进行数学建模, 为之后对扬声器的频率特性进一步分析打下基础。
扩展32KRAM的STC8H8K信号采集版: https://blog.csdn.net/zhuoqingjoking97298/article/details/105798094?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22105798094%22%2C%22source%22%3A%22zhuoqingjoking97298%22%7D