是否单个神经元可以识别手写体数字？

 MNIST识别

一、背景介绍

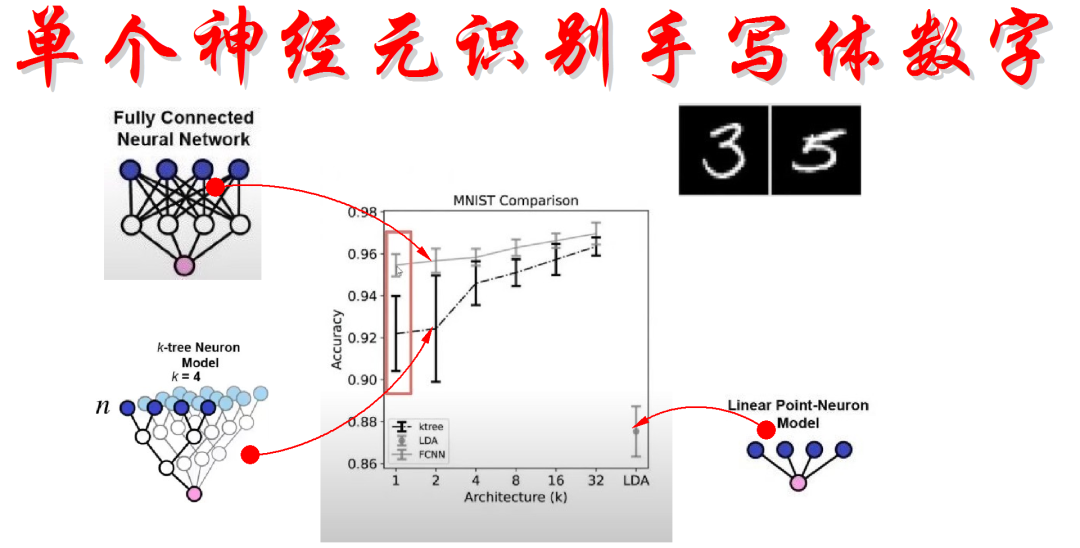
  今天看到一段视频，介绍一位来自美国Dartmouth大学神经科学专业学生的研究工作，现在约翰霍普金斯做研究员。 在Pennsylvannia大学研究神经计算。这个讲座来自于她介绍如何利用神经元生物特性完成神经网络学习。 但并不是对十个数字都进行识别， 而只是对其中的3,5 两个数字进行区分识别。 识别的效果如何呢？ 这里给出对比的结果。 这是线性分类器，实际上就是使用传统的单个神经元进行分类的准确率。已经能够接近于88%了。很不错了。 这是利用单隐层全连接BP网络的分类结果，可以看当中间隐层达到32的时候，准确率可以接近于98%。 中间这个是单个神经元识别的结果。 这里的单个神经元，比传统的单个神经识别效率高，究竟为什么呢？ 下面让我们看看Alina的工作吧。

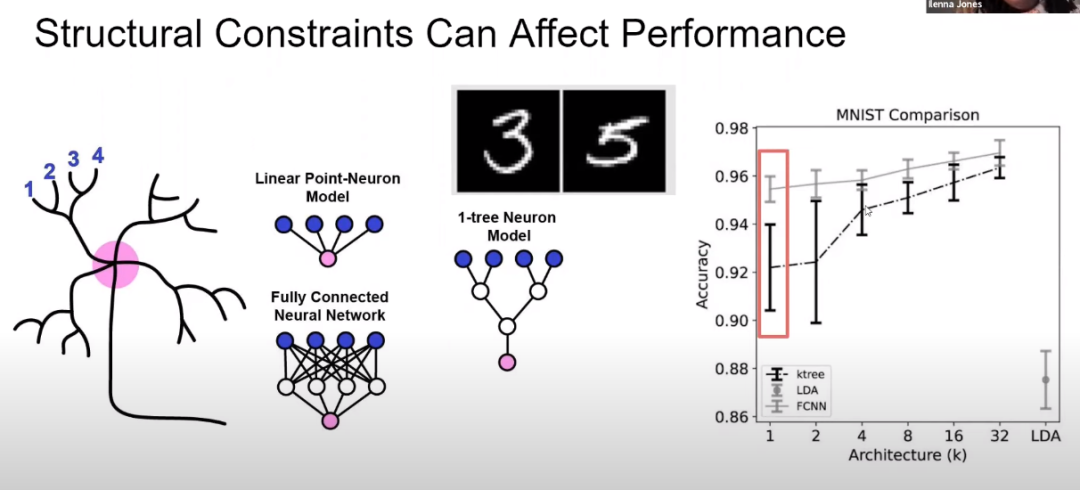
  在介绍具体工作之前，先看看这三个结果对应着什么神经网络。 这是传统的单个神经元， 它实际上是能够实现线性分类器。 所以对应的最好的分类结果是88%左右。 这是单隐层全连接网络， 它的识别结果最高。 这是本文将介绍的单个神经元， 这就令我们感到奇怪了。这难道不是一个深层网络吗？ 好吧，我们知道做理论研究最重要的是能够自圆其说。剩下的就是玩得高兴，不要太较真了。

二、单个神经元模型

  这是人大脑中的不同神经元的形态结构， 但现代人工神经网络则将神经元处理信息的功能进行了简化。  将不同形态的神经元看成由输入输入信息，轴突输出信息的多输入单输出系统。 输入信息经过比例加权之后，  然后在通过一个非线性激励函数输出。 这个模型被称为传统的 McCulloch-Pitts 模型。 它将神经元本身的多样性， 处理信息的多层次， 以及其它一些动态特性进行了省略， 所以现代神经网络中的神经元最终退化成只能完成线性分类的感知机。

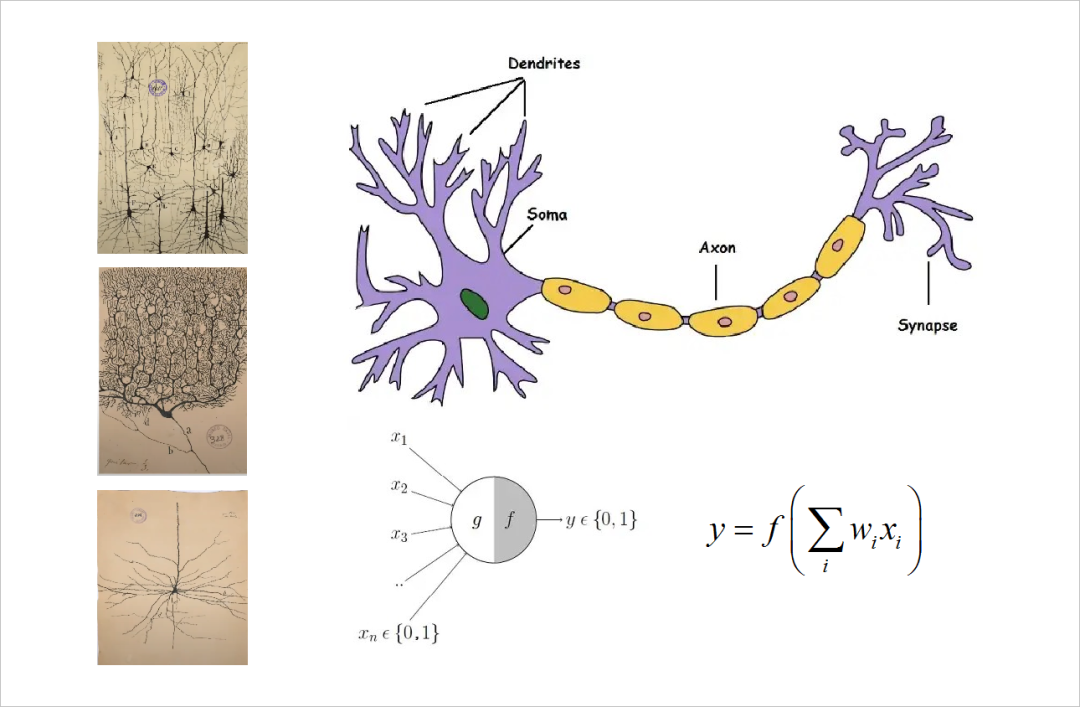
  关于生物神经元的细节，Alina进行了介绍，不过我对此并不太了解， 下面将给出Alina在McCulloch-Pitts模型上所做的五点改动进行介绍，并给出她的对比效果。 这是对单个神经元模型的五点改动。 先看前两点的改动，这是比较关键。 第一点将单个神经元从输入到输出看成一个二叉树。 信息从输入到输出之间经过若干层的综合处理。 传统意义上对于传递信息的轴突，也可以通过改变其电流传送阻抗完成对信息的加权， 因为轴突传送过程中的非线性也给这些汇聚点提供了非线性传递函数的功能。 因此就形成了深层信息处理的结构。 

        第二个改动是令我之前所不知道的，就是突触重复。 所谓的重复，就是突触在接收前级信息的时候会对若干个接触点输入信息进行平均。 因此就形成了输入信号的多次输入重复输入版本。 在汇合前各自有各自的传输通道。 因此在神经元模型中，就形成了多个相同的二叉树的并联， 这是重复两次的情况，  重复的次数k可以是任意设定的数值。这样就大大增加了单个神经元中可以修改的自由权系数的个数了。

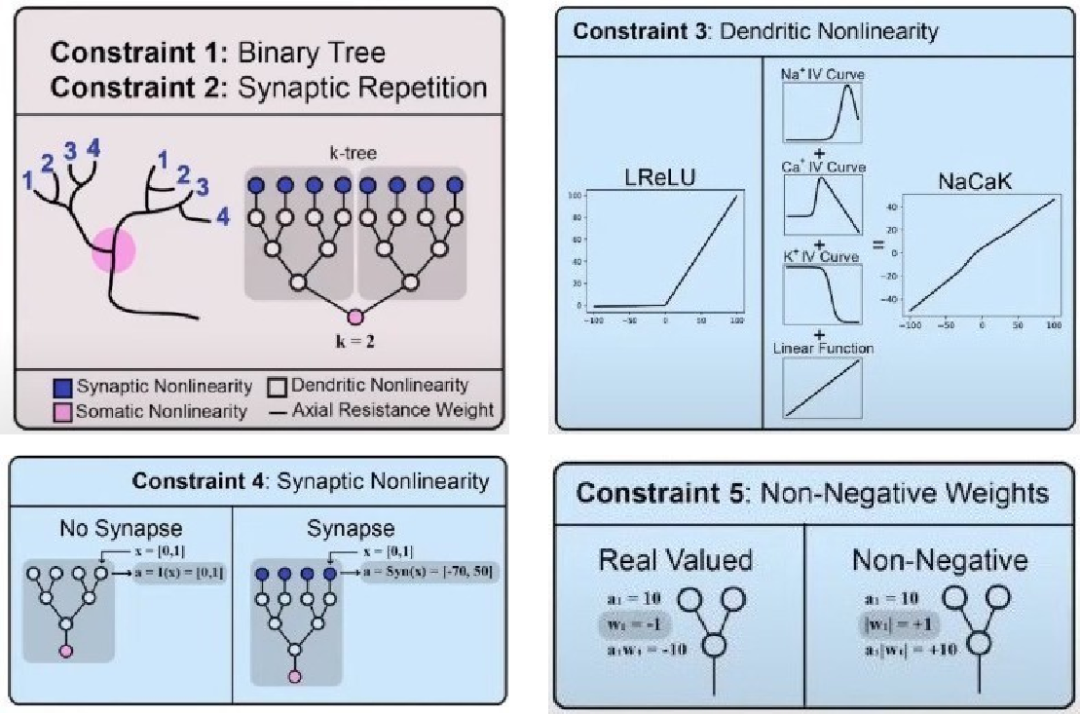
  下面在讨论一下 第三个神经元模型的修改。 传统神经元网络认为神经元的树突仅仅是对信号的汇聚环传输， 它应该是一个线性函数， 但实际上它传输信号过程中具有非线性， 这是去掉线性关系放大后的非线性， 实际上也可以形成类似于常见到的神经元传递函数。 这种传递函数是连续可导的。

         神经元的第四点修改， 是对输入层的功能调整。 传统神经元的输入层仅仅是将信号传递到网络，是个恒等关系， 但实际上信号进入神经元具有非线性关系， 这里给出的是动态微分方程， 如果考虑到静态关系则是一个具有五个参数的指数关系， 所以这一层也具有五个可以调整的权系数。 由此又增加了一层信息处理功能。

  下面来看看最后一个修改， 这是对权系数的限定， 在实际过程中所有的权系数都是正的数值， 这与通常神经元模型不同， 这是对神经元轴突信息处理特性的描述。 这个限制在一定程度上减少了神经元的模型复杂度。 这是考虑到实际生物神经元特性之后对神经元模型的五点修改。

三、修改后的效果

  经过上述对神经元模型的改造， 首先将单个感知机编程了多个二叉树的网络，其中可以调整的权系数就大大增加了。 这个模型相比于多层全连接的网络来讲，它属于稀疏网络， 对于MNIST中3,5两个数字的分类问题， 这三种网络的性能时有区别的， 从这个对比来来看，改造后的神经元的性能已经与多层全连接神经网络接近了。

※ 总  结 ※

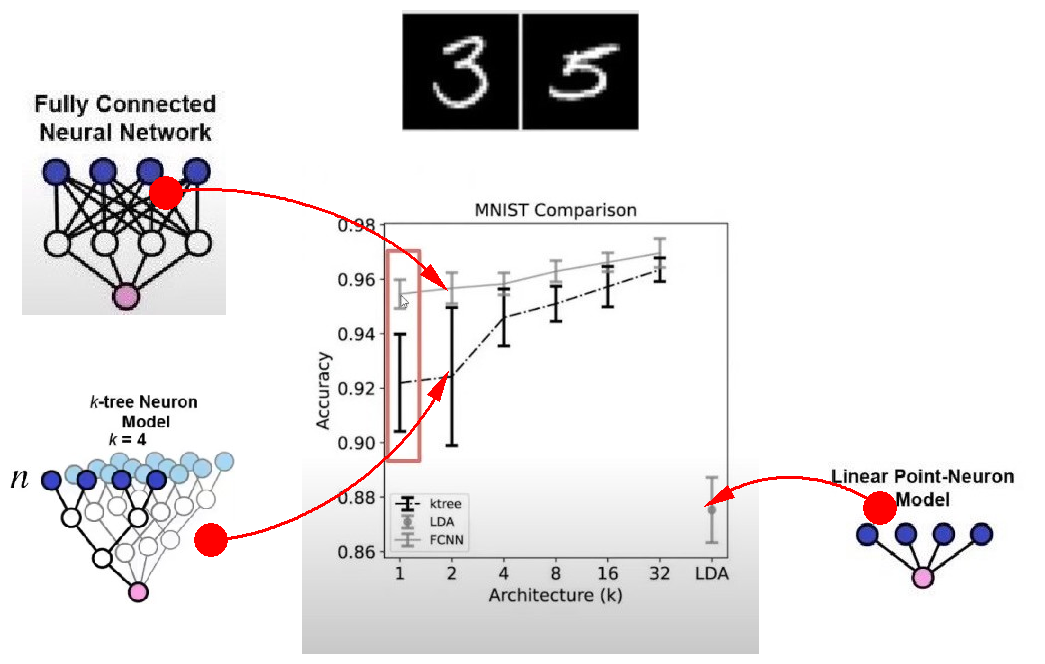
  本文介绍了艾莉娜·琼斯对于神经元模型的改进， 原视频中还通过大量的测试对比了每种改动对于识别效果的影响。 通过这样的神经元模型，的确可以实现单个神经元就可以完成MNIST中数字的识别效果。 对此你有什么看法吗？

参考资料