在本文中，考虑到非理想的车与车之间的通信，如通信延迟和数据包丢失，提出了一个用于联网自动驾驶车辆（CAVs）的基于事件触发的车辆跟踪控制方案。为减少计算负担，采用了基于输出的事件触发机制。通过与多目标控制器相结合，提出了事件触发模型预测控制（ETMPC），用于CAVs的横向和纵向车辆跟踪控制。仿真结果表明，与传统模型预测控制器相比，所提ETMPC在保持跟踪精度的同时，减少了61.5%的计算量，避免了不必要的优化操作。所提出的控制方案也可应用于车辆队列控制。
联网自动驾驶汽 车(CAVs) 已经引 起了极 大的关注，因为它们有可能提高运 输效率和安全性，并降低能源消耗[1]。这些都是通过自主CAV与周围环境之间的信息沟通来实现的[2]。
一辆CAV沿着预先计划好的轨迹行驶，实时的转向角和纵向力由自动驾驶控制器计算。通常情况下，目标轨迹是根据从摄像机和激光雷达等传感器获得的感知信息生成的。利用V2X (Vehicle-to- Everything)通信技术，自主CAV可以获取前一辆车的状态信息，直接将前一辆车作为跟踪目标[3]。
车辆跟随控制系统使车辆能够跟随前车行驶。轨迹跟踪控制问题可以被表述为纵向控制、横向控制和偏航控制。纵向控制是为了保持自驾车和前车之间的目标距离[4] 。自动纵向控制已被广泛研究，如自适应巡航控制（ACC）和自主紧急制动（AEB）。横向控制和偏航控制的目的是减少横向跟踪和航向角误差，它们通常被认为是广义的横向控制[5]。
横向跟踪控制在车辆跟踪系统中起着关键作用。模型预测控制(MPC)由于能够处理显式约束和后视界优化带来的高控制精度，被广泛应用于横向控制。然而，MPC方法在每个时间步都是对有限控制序列求解，计算量大，在线可实现性差。因此，传统MPC的计算效 率提 高是非常值得期待的。
处理上述问题的一种可能方法是使用事件触发机制(ETM)，使用该机制，在线优化推导只在必要时基于预定义条件[7]执行。ETM能够减少计算负担，同时保持理想的控制性能。根据被控对象的特点，ETM可以是基于输出的，也可以是基于观测的[8]。其稳定性已在文献中得到证明[9]。尽管ETM已被广泛用于网络系统控制和状态估计[10]，但ETM和MPC的结合却很少被用于车辆跟踪控制。
本文研究了车对车（V2V）通信下的CAV的车辆跟随控制。拟议的车辆跟踪控制方案的原理图如图1所示。前方车辆的位置、速度、加速度、航向角和偏航率信息可以通过V2V通信传输。考虑了包括传输延迟和丢包在内的有损通信环境。提出了一种线性参数变化模型预测控制（LPV-MPC）方法用于横向跟踪控制，而纵向跟踪控制则由一个多目标控制器实现。通过整合纵向和横向跟踪控制器来补偿有损的通信。提出了一个基于输出的ETM，以减少拟议控制器的计算负担，同时保持跟踪精度。所提出的车辆跟踪控制方案的有效性在综合模拟场景中得到了验证。
本文的其余部分安排如下：第二节介绍了非理想的V2V通信架构。第Ⅲ节阐述了车辆动力学模型和所提出的事件触发式车辆跟踪控制器。第Ⅳ节介绍了验证结果，随后第Ⅴ节总结了主要结论。
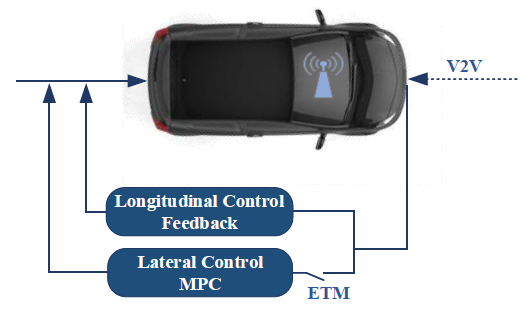
图1 车辆跟踪控制方案的示意图。
在实践中，V2V通信可能会受到各种因素的影响，这往往会导致不可忽视的通信延迟和数据包丢失[11]。这些通信延迟可被视为端对端延迟，即从始发节点到目标节 点的信号传输时间。对于车辆跟踪控制，从前车到自车的信号传输被称为单跳[12]。在文献中,各种延迟被描述为具有三个参数的Burr分布Burr(a, b, c)[13]，它由以下公式给出：
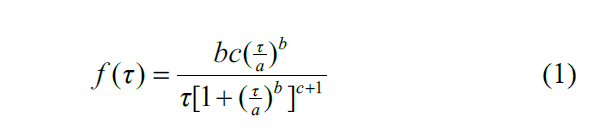
其中，a是比例参数；band关心形式参数；τ是单跳延迟。单跳时延的概率分布如图2所示，可以描述为Burr（2.72, 17.20, 0.20）。
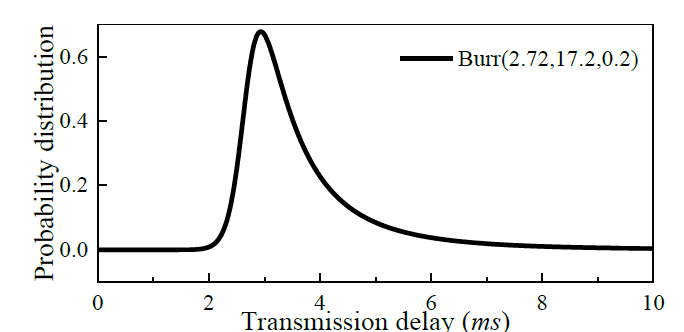
图2 传输延迟。
数据包丢失率代表成功传输的数据占总传输数据的比例，它反映了V2V通信的质量和可靠性。对于无线通信，丢包的主要因素是信号的功率强度下降。根据对丢包 的分析，丢包率可以被建模为[13] 。
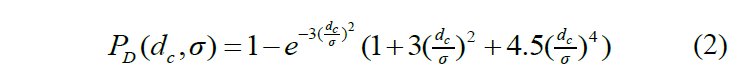
其中dc为通信距离；为传输特性参数。σ将随着信道传输质量的下降和车辆速度的增加而增加。图3显示了相对于距离的下降率变化。在本研究中，σ=480是根据高速公路驾驶情况选择的。
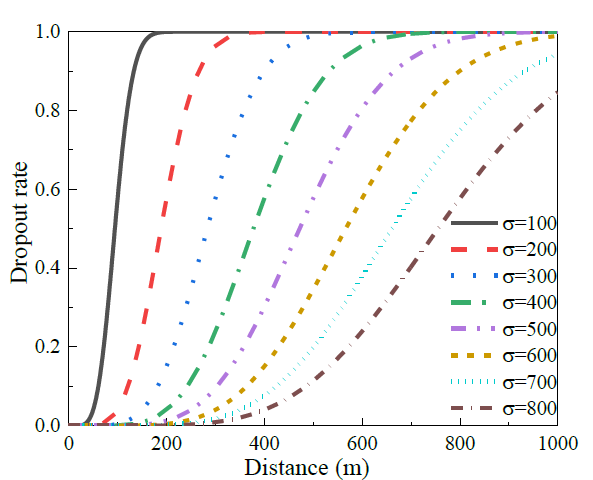
图3：单跳中的丢包率。
对于车辆跟踪控制，前车的状态是必要的，其中包括 位置、速度、加速度、航向角和偏航率。对于MPC的实施，需要一个前车的参考序列。然而，V2V通信周期为100毫秒，而自主CAV的控制周期为10毫秒。因此，前车在过去1秒内的历史状态通过V2V通信传输，如图4所示。
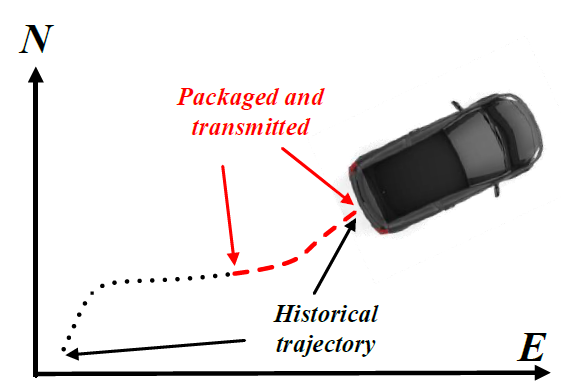
图4 V2V通信的传输模块。
利用前面车辆传输的历史轨迹，与自主CAV的位置信息相比，最近的目标航点被准确定位。
III.事件触发的车辆跟踪控制器
如图5所示，一个三自由度（3-DoF）车辆模型被用来表示车辆动力学[14]。在这个模型中, Fyf 和 Fyr 是前后轮的侧向力；Fxf 和 Fxr 是前后轮的纵向力 ；αf和 αr 是前后轮的滑移角 ；δf 是前轮的转向角 。ψ是车辆的偏航率 ；ψ是车辆的航向角 ；v 和 v y 是车辆的纵向和横向速度 ；l f 和 l r 是重心纵向控制的距离 。( C o G ) 到前轴和后轴的距离；X - Y 是车辆坐标；X - Y 是大地测量坐标 。
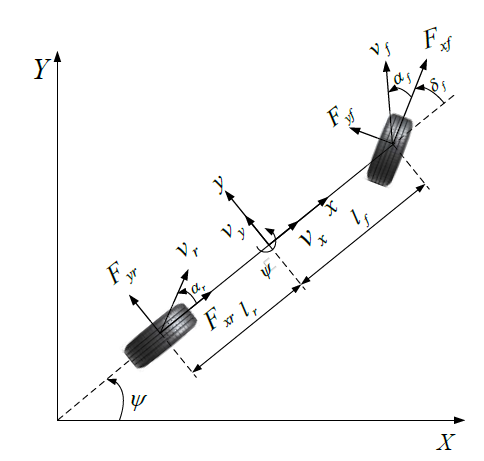
图5 采用的3-DoFhicled动力学模型。
根据3-DoF模型，运动方程可由以下公式给出
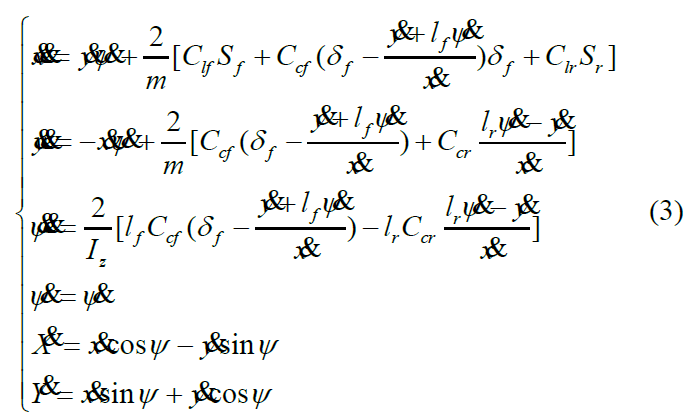
其中Clf 和 Clr 是前后轮胎的纵向刚度；Ccf 和Ccr 是前后轮胎的横向刚度；m是车辆的质量；Iz 是车辆的转动惯量。它可以被进一步重新表述为
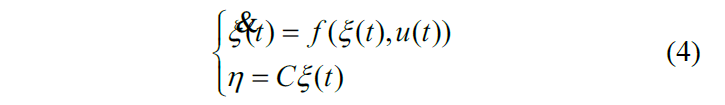
我们提出了一个用于纵向运动控制的反馈控制器。纵向速度和加速度以及车辆间的距离被选作控制器的反馈变 量。对于时间变化的跟踪距离，采用了一个恒定的时间头程政策，该政策由以下公式给出
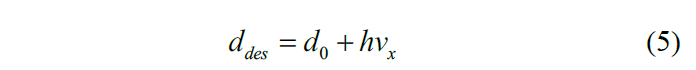
其中 ddes 是期望的跟踪距离 ；d0是静止的车辆间距离 ；h 是时间头程。追踪距离和相对速度的误差被定义为
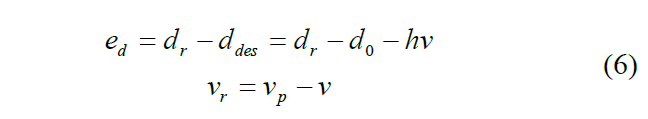
其中ed是跟踪距离误差；vr 是相对速度误差；
dr是实际跟踪距离；vp是前车的速度 。
自主CAV的期望纵向加速度推导为[15] 。
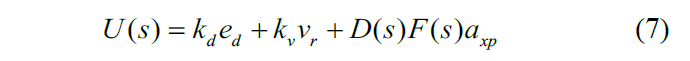
其中kd 和 kv 是反馈参数；axp 是前车的纵向加速度；D(s)=e-τs 是时变的V2V通信延迟 ；F(s) 是延迟补偿器，它由以下公式给出
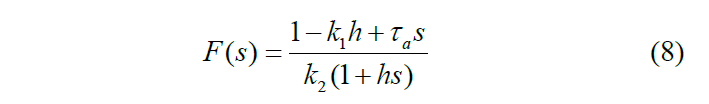
其中k1 and k2是特征参数 ；τa是执行器延迟
C.事件触发的侧向车辆跟踪控制器
前面车辆的侧向跟踪参考与偏航率、航向角和侧向位移相结合。采用坐标转移函数，根据大地坐标中的位置 ，计算前车在自主CAV坐标中的横向位移，其公式为
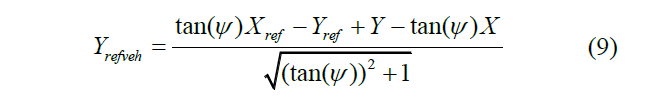
其中 Yrefveh 是前车在自主 CAV 坐标中的横向位移 。
参考输出矢量给定为：
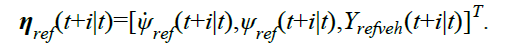
根据公式（4），离散形式的增强模型预测方程被构建为：
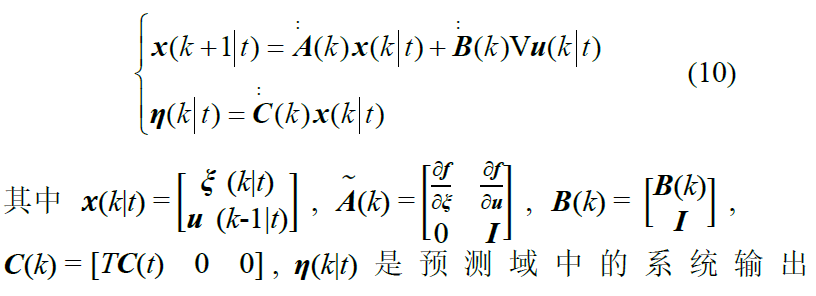
假设Np是预测域，Nc是控制域，Nc≤Np，系统输出可以得出：
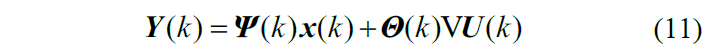
其中
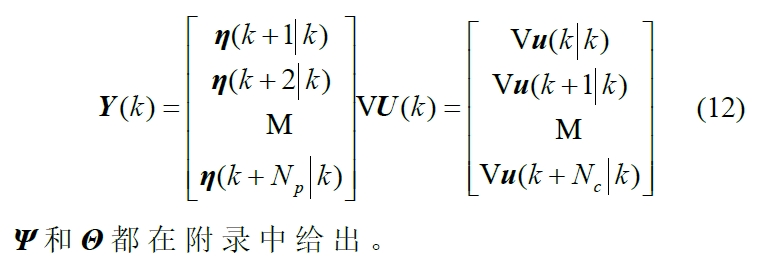
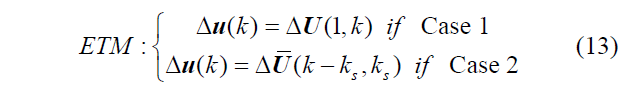
ΔUi是当前时间步骤的优化方案；ΔU转化为前一个被触发的时间步骤的优化方 案；ks 是上一个被触发事件的时间步长。图6显示了拟议的ETM的详细方案。
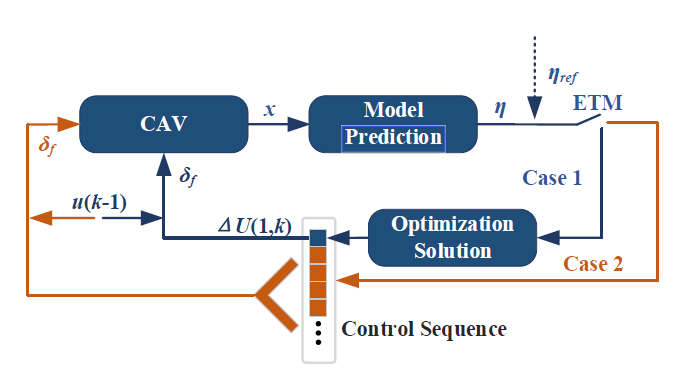
图6 拟议的ETM方案。
以下是两个案例：
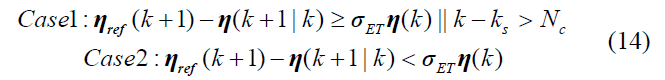
其中 0<σET<1 是一个调整参数。
任意 kϵ[ks,ks+1）， 一旦系统输出满足Case2，即将触发的事件的时间步长应该是
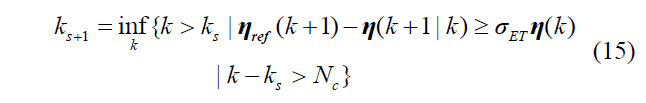
可见，{𝑘𝑠}𝑠∞=0 ⊆ {0 ∪ ℤ+} 是非周期性的, 事件触发的时间常数不超过周期触发的时间常数 。
触发频率由调谐参数σET.决定。σET =0 对应于一个特殊的状态，在这个状态下，ETM相当于一个传统的周期触发的实现。
随着σET增加，执行优化的数量可以减少；但如果σET超过一定范围 ,跟踪的稳定性和精度可能会大大降低 。
一旦触发事件发生，执行优化以获得最优控制序列。最佳目标是使参考轨迹与预测轨迹之间的偏差最小化。为了提高收敛速度，引入了松弛因子。优化目标函数定义为
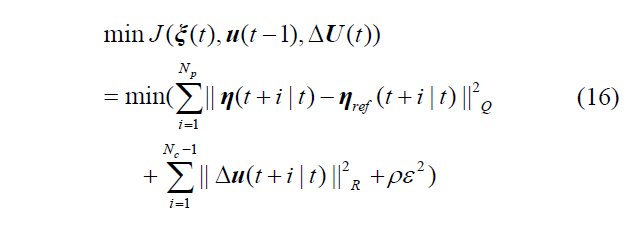
其中Q∈R3×3 and R∈R2×2 是跟踪精度和控制增量的加权矩阵；ε>0 是松弛因子；ρ是松弛因子的加权系数 。
本研究采用序列二次方程（SQP）方法[16]， 目标函数为二次方程 ，其公式为
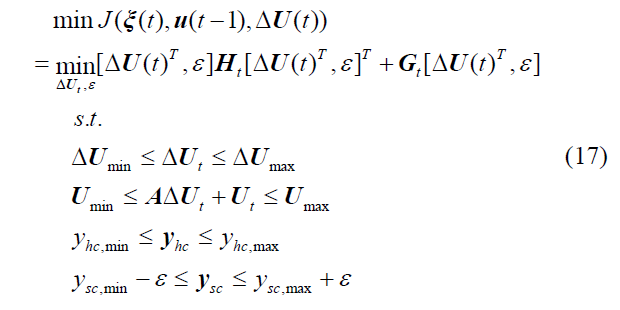其中∆Ut 是增量控制变量；Ut 是控制变量；yhc硬约束 ; ysc是软约束；以及
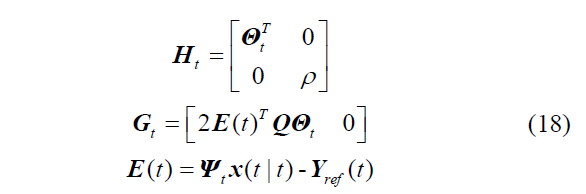
利用增量控制序列中的第一个控制变量计算实际控制变量
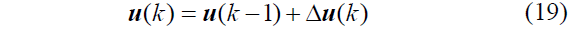
最后，得到了自主CAV的输入转向角度。
IV.仿真验证
为验证所提出的事件触发车辆跟踪控制方案的有效性，进行了综合试验。在Simulink环境中对通信延迟和数据包丢失进行建模。采用传统的MPC车辆跟踪方法进行比较。
图7显示了V2V通信数据包丢失的影响，其中显示了前车的纵向速度和丢失的时间瞬间，信号更新暂停是由于V2V通信的数据包丢失。
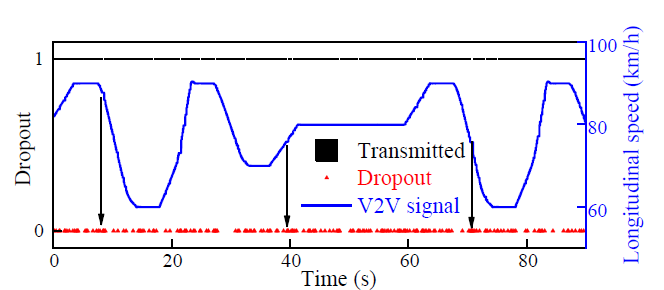
根据第二节的通信延迟模型，V2V的通信延迟在大多数情况下都小于10ms。CAV的控制周期为10毫秒 。
因此，一个零阶保持（ZOH）被应用于延迟信号。这就是说，一旦发生延迟，就假定有一个周期的延迟。
仿真的参数见表Ⅰ。
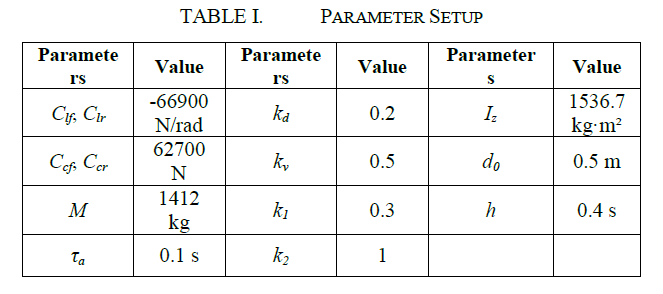
为了检验所提出的事件触发车辆跟踪控制方案的性能，在美国联邦公路管理局（FHWA）的Alt3公路上执行了一个弯道机动。
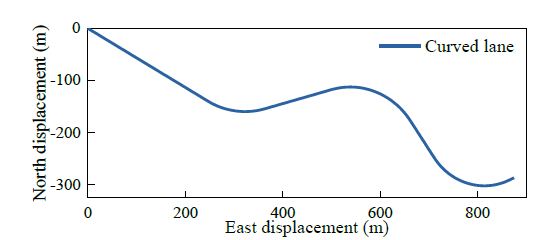
图8.弯道
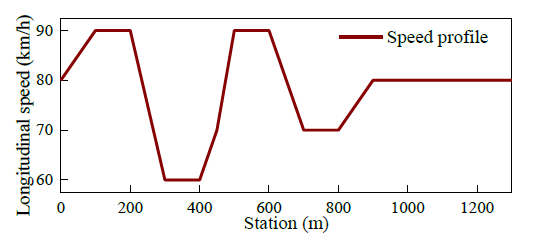
图10(a )显示了使用两种方法在每个时期的计算时间。很明显，传统MPC的计算时间在3毫秒到8毫秒之间，而ETMPC的计算时间几乎不在这个范围内。相反，ETMPC的大部分计算时间在1万到2毫秒之间，这意味着在这些期间不会执行优化推导。图10(b)对ETM做了更直观的描述 ，其中间隔是指两个相邻的触发时间步骤之间的控制期数，即公式 （14）中的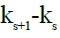
。
作为反映ETM影响的一个典型例子，44秒和46秒之间的间隔在1和4之间变化。大多数的间隔是2，这意味着优化实施每两个控制期才执行一次。这正是两种方案的计算效率不同的原因。
如上所述，ETMPC显示了减少计算负担的能力；但它仍能保持类似的跟踪精度。图10(c-f)显示了两种方法在横向跟踪误差、转向角、纵向速度和纵向车距方面的跟踪性能。可以看出，尽管横向跟踪误差稍大，但ETMPC具有与传统MPC相同的转向角和纵向速度。
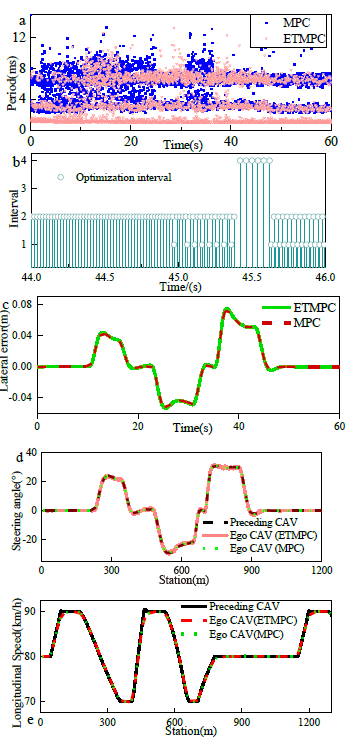
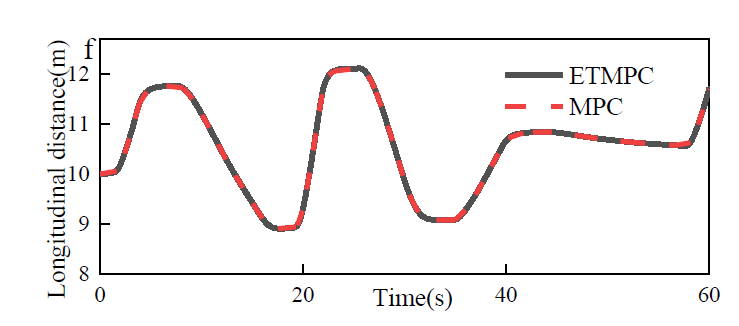
图10 仿真结果：(a)耗时；(b)控制间隔；(c) 横向跟踪误差；(d) 转向角；(e) 纵向速度；(f) 纵向的车辆距离。
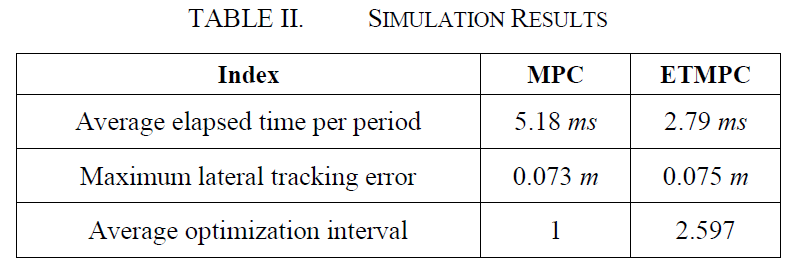
两种控制方案下的详细模拟结果见表Ⅱ。MPC和ETMPC每期的平均计算时间分别为5.18ms和2.79ms。ETMPC的 平均优化间隔为2.597，减少了61.5%的不必要的优化实施。这些研究证明了ETMPC在提高计算效率方面的能力 。这两种方法的最大横向跟踪误差几乎相同，分别为0. 073米和0.075米，这证明了ETMPC可以保证类似的跟踪精度，同时减少计算强度。
V.总结
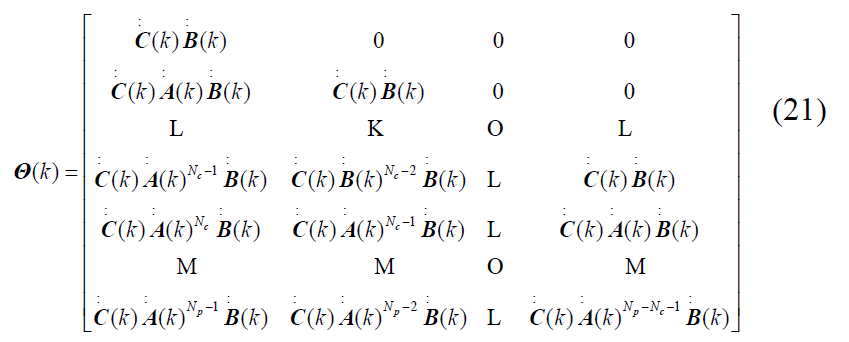
参考文献：
[1] T. Ersal et al., "Connected and automated road vehicles: state of the art and future challenges," Vehicle System Dynamics, pp. 1-33, 2020.
[2] J. Guanetti, Y. Kim, and F. Borrelli, "Control of connected and automated vehicles: State of the art and future challenges," Annual Reviews in Control, vol. 45, pp. 18-40, 2018/01/01/ 2018.
[3] S. E. Li et al., "Dynamical Modeling and Distributed Control of Connected and Automated Vehicles: Challenges and Opportunities," IEEE Intelligent Transportation Systems Magazine, vol. 9, no. 3, pp. 46-58, 2017.
[4] Z. Wang, Y. Bian, S. E. Shladover, G. Wu, S. E. Li, and M. J. Barth, "A Survey on Cooperative Longitudinal Motion Control of Multiple Connected and Automated Vehicles," IEEE Intelligent Transportation Systems Magazine, vol. 12, no. 1, pp. 4-24, 2020.
[5] R. Rajamani, T. Han-Shue, L. Boon Kait, and Z. Wei-Bin, "Demonstration of integrated longitudinal and lateral control for the operation of automated vehicles in platoons," IEEE Transactions on Control Systems Technology, vol. 8, no. 4, pp. 695-708, 2000.
[6] D. Bevly et al., "Lane Change and Merge Maneuvers for Connected and Automated Vehicles: A Survey," IEEE Transactions on Intelligent Vehicles, vol. 1, no. 1, pp. 105-120, 2016.
[7] H. Zhang, G. Feng, H. Yan, and Q. Chen, "Observer-Based Output Feedback Event-Triggered Control for Consensus of Multi-Agent Systems," IEEE Transactions on Industrial Electronics, vol. 61, no. 9, pp. 4885-4894, 2014.
[8] W. P. M. H. Heemels, K. H. Johansson, and P. Tabuada, "An introduction to event-triggered and self-triggered control," in 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), 2012: IEEE.
[9] R. Yang and W. X. Zheng, "Output-Based Event-Triggered Predictive Control for Networked Control Systems," IEEE Transactions on Industrial Electronics, vol. 67, no. 12, pp. 10631-10640, 2020.
[10] R. Yang, H. Zhang, G. Feng, H. Yan, and Z. Wang, "Robust cooperative output regulation of multi-agent systems via adaptive event-triggered control," Automatica, vol. 102, pp. 129-136, 2019.
[11] H. Yang, X. Guo, L. Dai, and Y. Xia, "Event-triggered predictive control for networked control systems with network-induced delays and packet dropouts," International Journal of Robust and Nonlinear Control, vol. 28, no. 4, pp. 1350-1365, 2018.
[12] J. Zhang, S. Chai, and B. Zhang, "Model-based event-triggered dynamic output predictive control of networked uncertain systems with random delay," International Journal of Systems Science, vol. 51, no. 1, pp. 20-34, 2020.
[13] J. Shi, Y. Luo, Y. Qi, and K. Li, "A Model-based Description Method for Key Performance Indicators of DSRC System in Vehicle Platoons," Automotive Engineering, vol. 42, no. 11, pp. 1449-1457, 2020-11-25 2020.
[14] J. Liu, Z. Wang, L. Zhang, and P. Walker, "Sideslip angle estimation of ground vehicles: a comparative study," IET Control Theory & Applications, vol. 14, no. 20, pp. 3490-3505, 2020.
[15] S. Wei, Y. Zou, X. Zhang, T. Zhang, and X. Li, "An Integrated Longitudinal and Lateral Vehicle Following Control System With Radar and Vehicle-to-Vehicle Communication," IEEE Transactions on Vehicular Technology, vol. 68, no. 2, pp. 1116-1127, 2019.
[16] J. Liu, Z. Wang, Y. Hou, C. Qu, J. Hong, and N. Lin, "Data-Driven Energy Management and Velocity Prediction for Four-Wheel-Independent-Driving Electric Vehicles," eTransportation, p. 100119, 2021.
分享不易，恳请点个【👍】和【在看】
