在昨天博文 使用数字示波器DS6104测量交流信号的幅值和相位[1] 中对于使用示波器测量正弦交流信号的幅值和相位进行了分析和实验研究。但是对测量出的幅值和相位结果中的误差随着示波器的时基( time base )不同而改变的原因,究竟是在博文第二部分分析中理论上存在的误差引起的,还是由于示波器本身在同步、AD位数精度、数据处理窗口方面引起的呢?
关于这个问题可以通过计算机仿真实验,对采集过程使用仿真来验证。

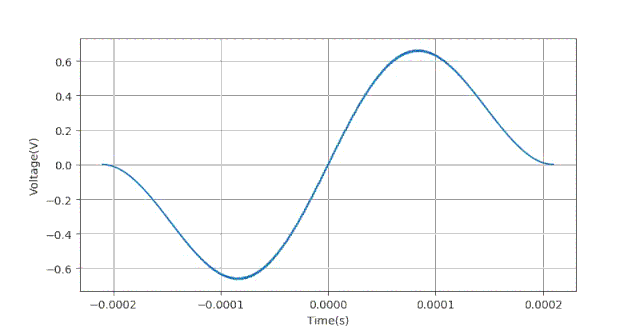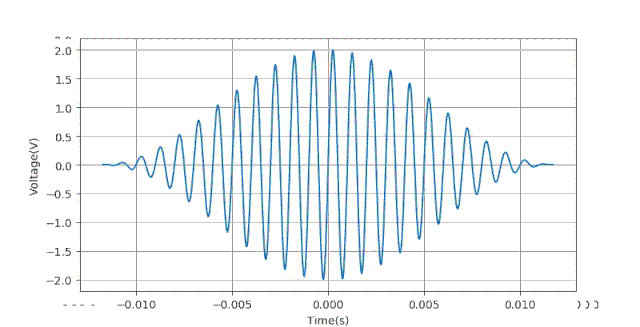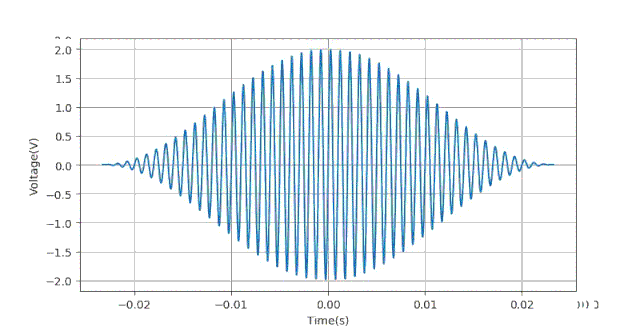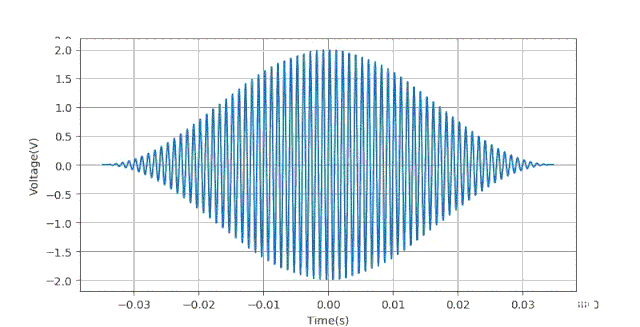
在实验中,根据DS6104示波器的参数,对于采集到的数据做一下假设:数据点个数 ,时基 对应100个数据采样点。信号的频率 ,相位 。数据的中心对应着时间t=0时刻,相当于信号触发同步的时间点位于示波器的中心。
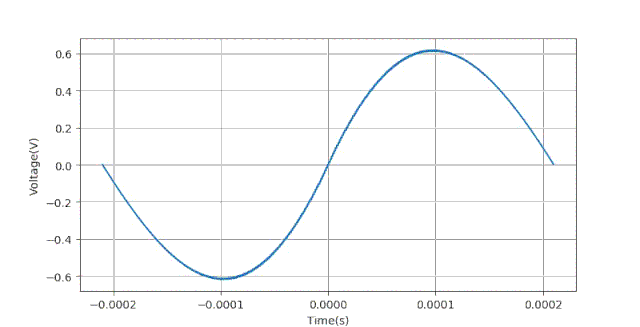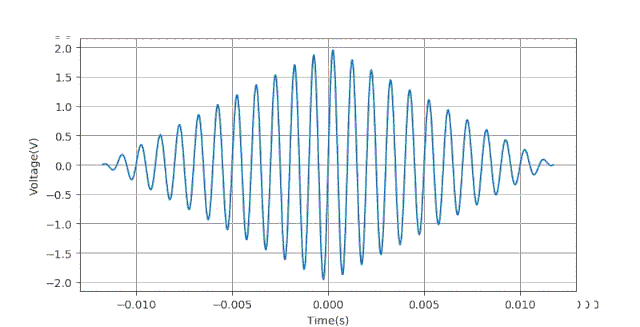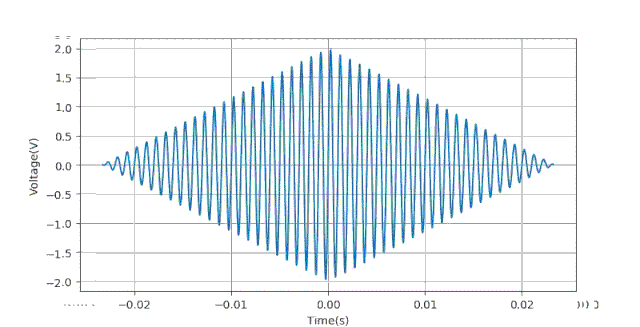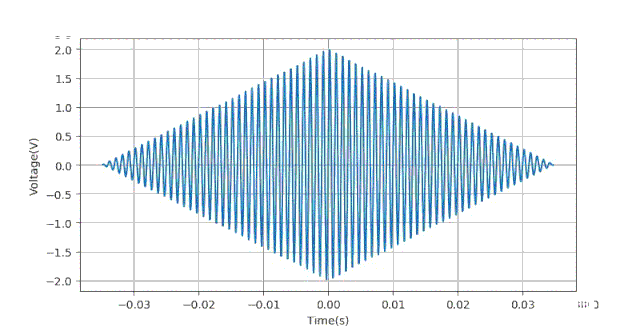
下面给出生成数据的Python语句:下面给出当ts=0.5ms时对应的数据波形。
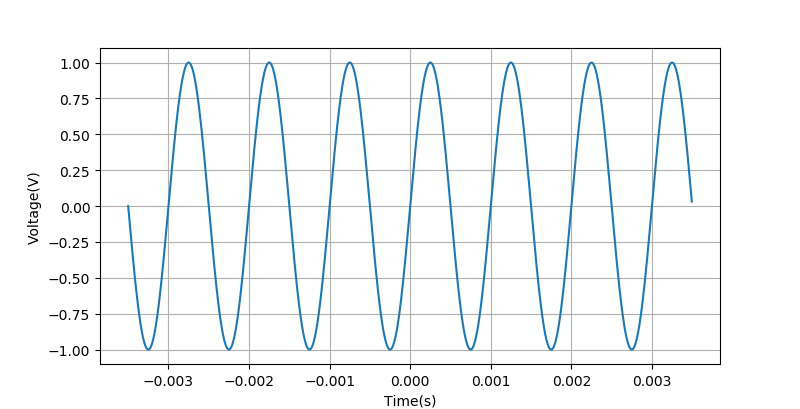
利用在博文 使用数字示波器DS6104测量交流信号的幅值和相位[1] 中的计算方法求信号的有效值和相位。
测量得到的信号有效值和相位分别是:
E = 0.7071067811865476, theta=-1.0150610510858574e-17
在示波器中,数据采集的位数为8位。下面对采集数据的位数分别从1~16进行仿真实验,验证采集数据的位数对测量的影响。
| 位数 | 有效值 | 相位 | 有效值误差 |
|---|---|---|---|
| 1 | 0.7821 | 0.0000 | 0.0750 |
| 2 | 0.7372 | 0.0000 | 0.0301 |
| 3 | 0.7189 | 0.0000 | 0.0118 |
| 4 | 0.7076 | 0.0000 | 0.0005 |
| 5 | 0.7075 | 0.0000 | 0.0004 |
| 6 | 0.7078 | 0.0000 | 0.0007 |
| 7 | 0.7072 | 0.0000 | 0.0001 |
| 8 | 0.7072 | 0.0000 | 0.0001 |
| 9 | 0.7069 | 0.0000 | -0.0002 |
| 10 | 0.7072 | 0.0000 | 0.0001 |
| 11 | 0.7070 | 0.0000 | -0.0001 |
| 12 | 0.7071 | 0.0000 | 0.0000 |
| 13 | 0.7071 | 0.0000 | -0.0000 |
| 14 | 0.7071 | 0.0000 | 0.0000 |
| 15 | 0.7071 | 0.0000 | -0.0000 |
| 16 | 0.7071 | 0.0000 | 0.0000 |
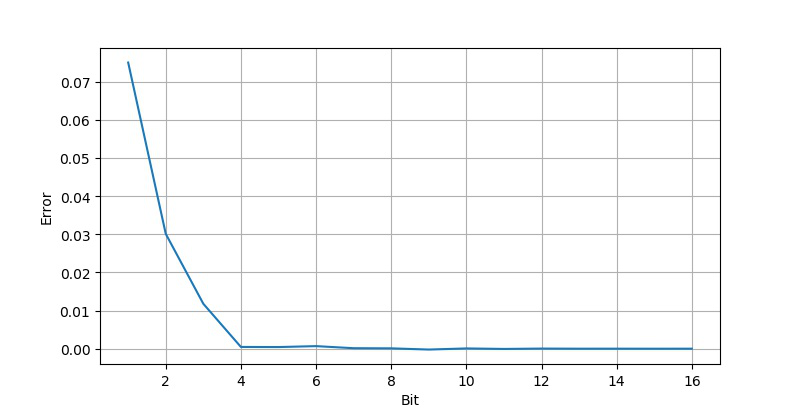
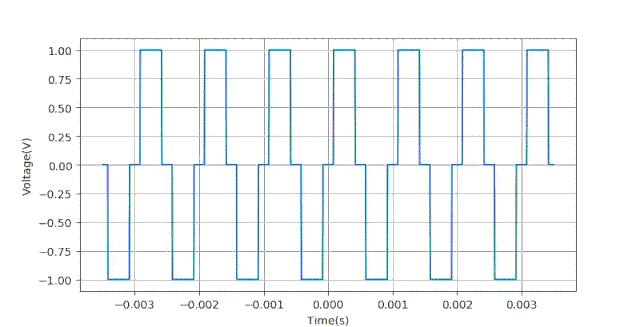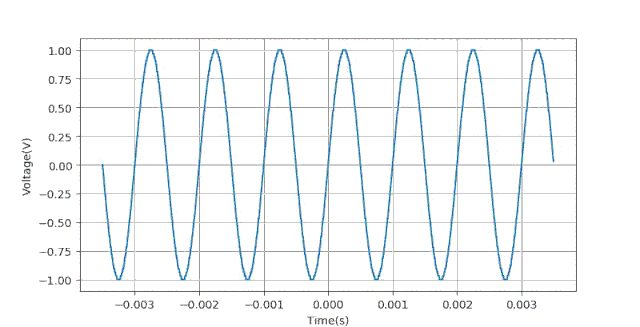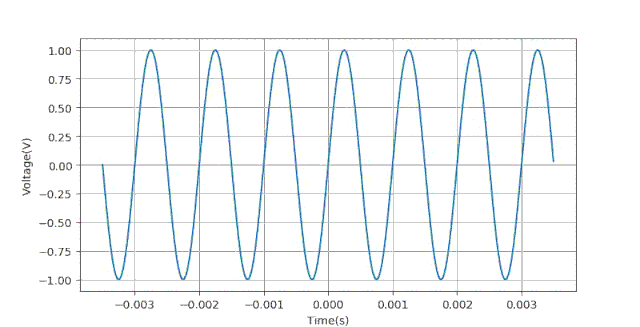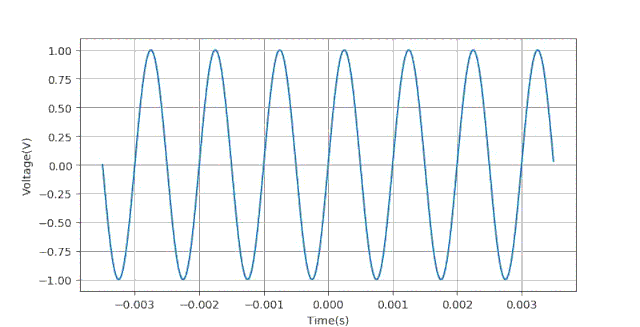
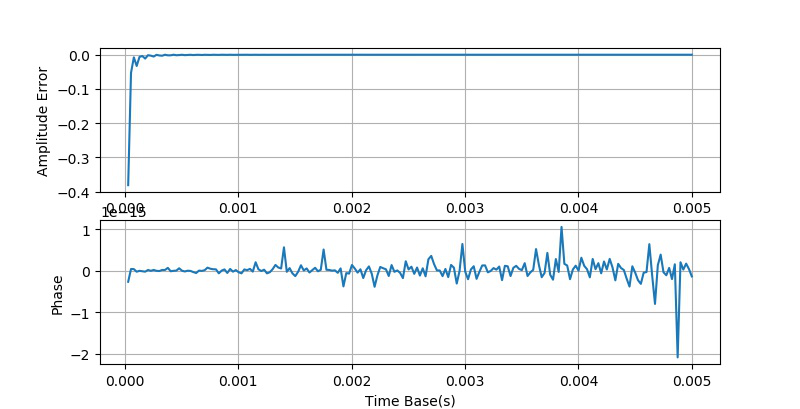
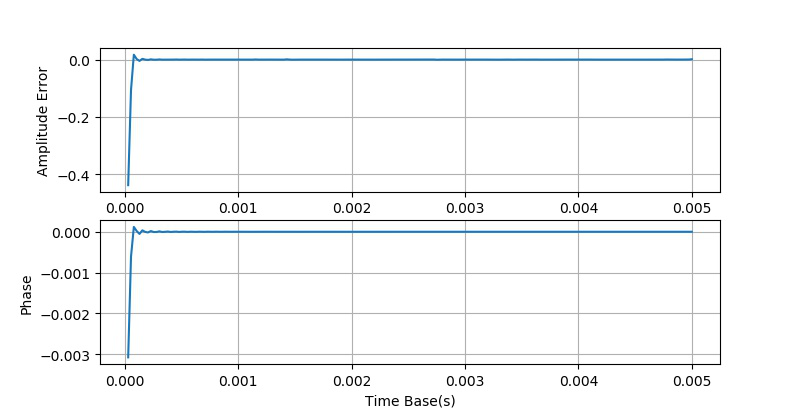
在下面的仿真中,采集量化位数 。时基从30us到5000us,采集200个实验点。
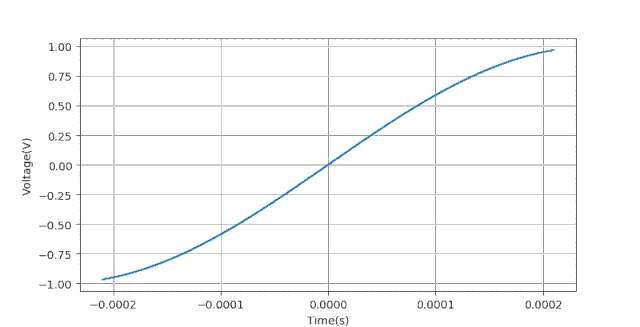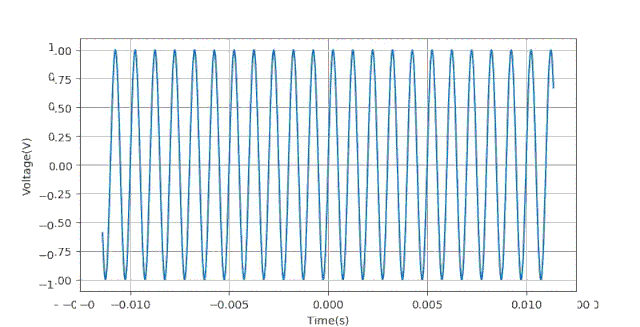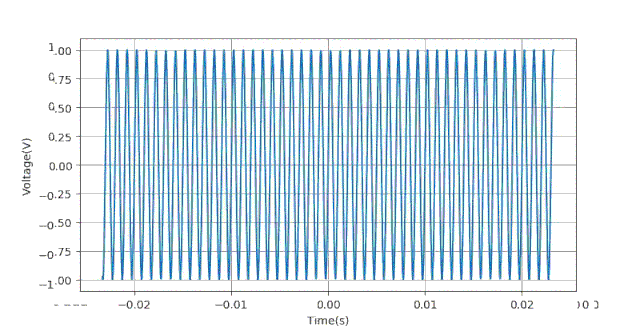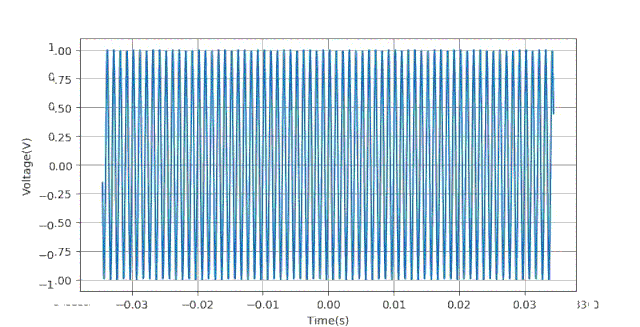
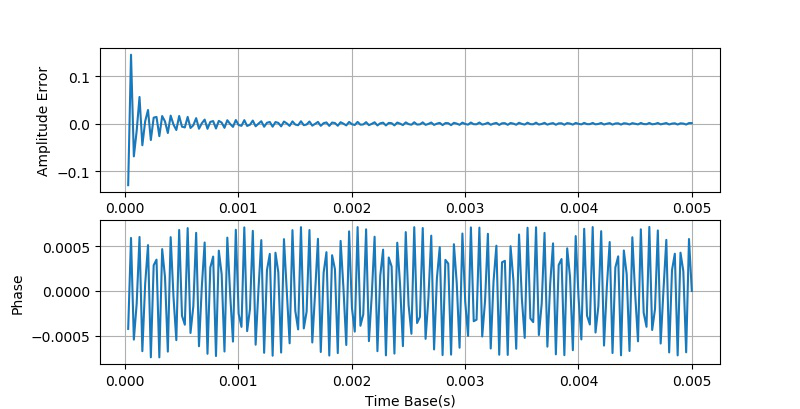
通过实验可以验证,如果取消量化过程,所得到的测量误差(幅值,相位)的情况与上面量化位数等于8时几乎一样。
对比在 使用数字示波器DS6104测量交流信号的幅值和相位[1] 中时基使用示波器测量的结果,可以看到,在ts<0.002s的时候,所得到的误差与仿真的结果仅此,但当ts大于0.002之后,所得到的误差就呈现了规律的锯齿波的形状。对于这个现象现在还无法解释。
通过对数据增加三角窗和 Hanning 窗口[2] 加权处理,来评估时基对参数计算误差。
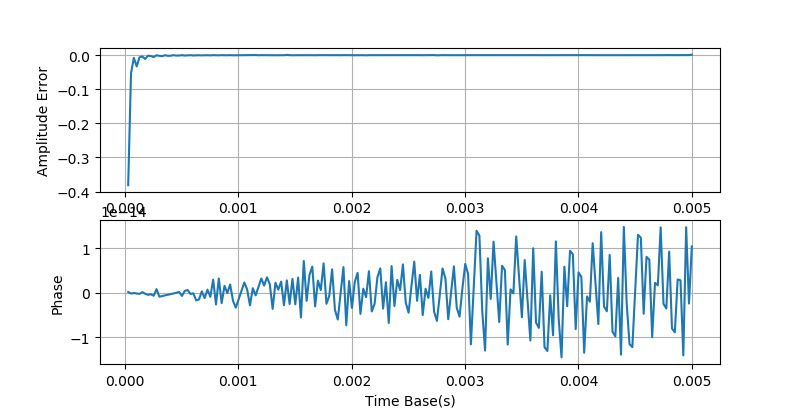
疑问: 为何三角窗口对于相位影响这么大?
猜测: 可能这个问题来自于对信号的量化误差所带来的。
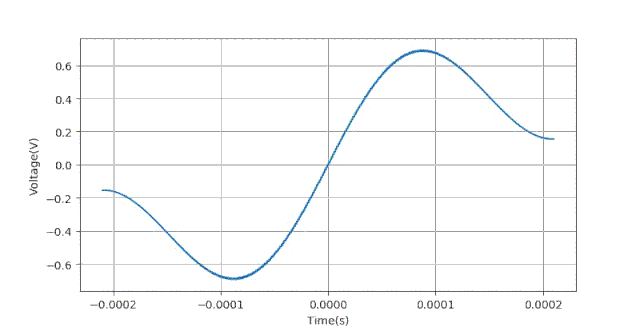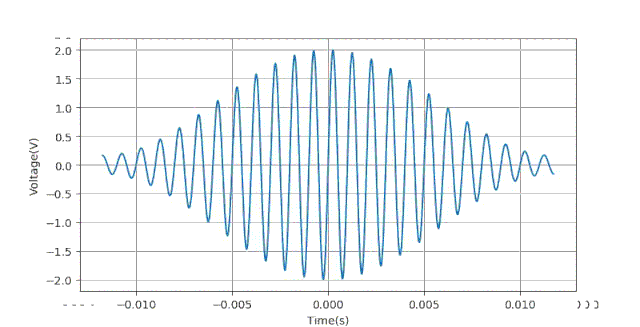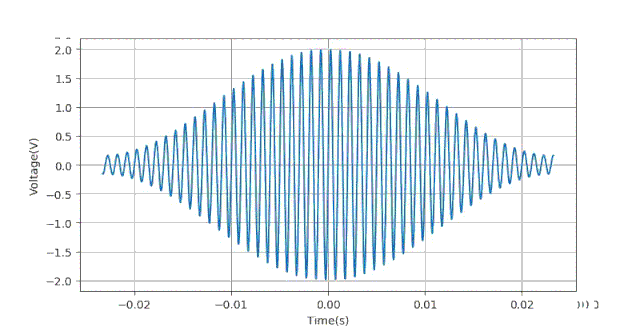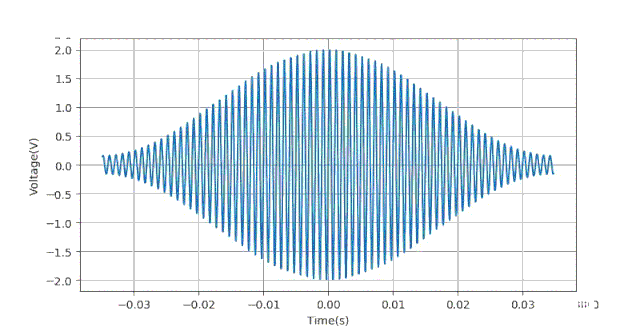

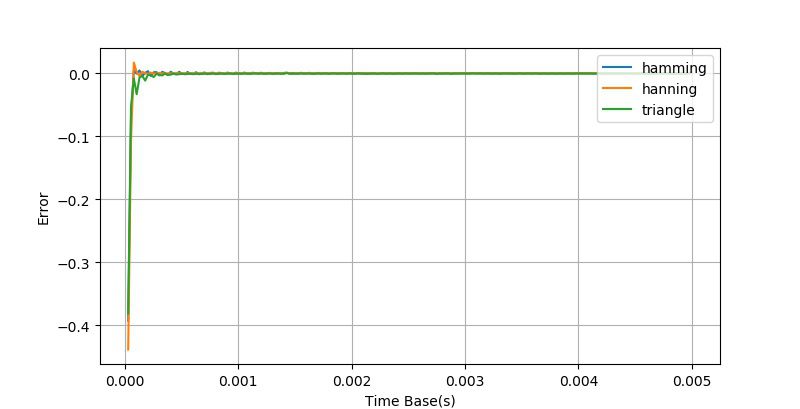
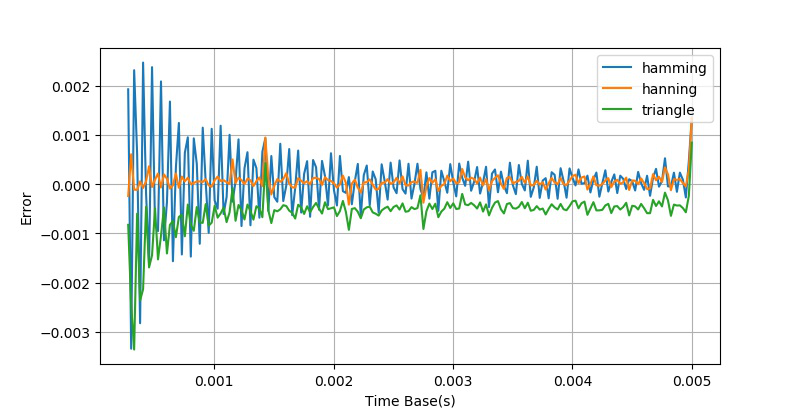
经过放大之后,我们看到上面的幅值误差曲线呈现了某种随机的情况。猜测这可能 与量化误差有关系,下面重新将上述加窗方法数据生成一边,只是将对信号的量化部分去除掉。绘制出三种加窗方法测量得到的误差曲线(局部)如下:
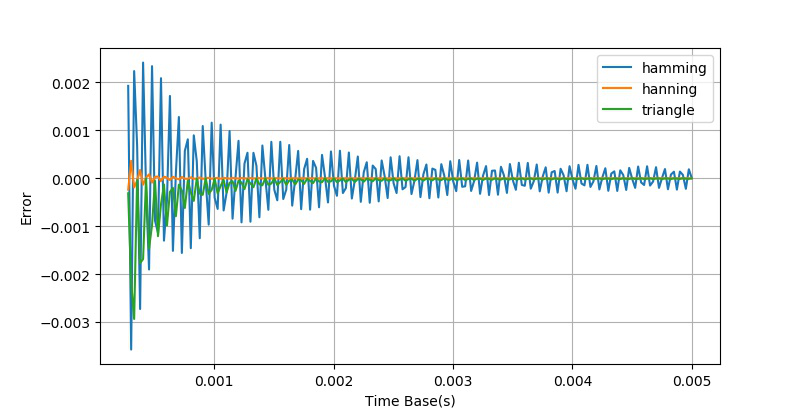
可以看到没有了量化误差,测量误差曲线与时基ts之间的关系变得有规律了,而不在呈现随机状态。
通过实验,可以看到在博文 使用数字示波器DS6104测量交流信号的幅值和相位[1] 中测量信号幅值和相位的过程中,时基ts对于测量误差的影响所出现的现象并不能够完全有理论仿真来解释。特别是对于ts大于0.002s之后出现的情况,应该与示波器本身的采集原理有关系。
这个分析也证实了,在实际工程实践中,除了理论部分分析之外,还需要考虑到实际测量过程所出现的其它异样的情况。
使用数字示波器DS6104测量交流信号的幅值和相位: https://zhuoqing.blog.csdn.net/article/details/106439663
[2]Hanning 窗口: https://dsp.stackexchange.com/questions/56400/hanning-and-hamming-window