记得上初中的时候,我们学习过方程组,那个时候只知道消元依次求解。
在大学的时候,我们又学习了线性代数,可以经过初等变换一次性求出所有解。
这篇文章主要是用C语言实现高斯列主元消去法求解多元一次方程。

假如现在有一个三元一次方程组,如下:
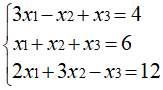
系数矩阵就是将方程组的系数组成矩阵。
下图即为行列式的增广矩阵:
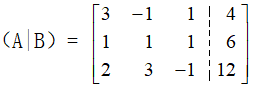
这里说的组上三角矩阵是指经过若干步初等变换,将矩阵左上角和右下角连线组成的对角线左下方的元素全部清零。
主元以及初等变换两个概念。主元指在消去过程中起主导作用的元素,主元通常选择绝对值最大的元素,用它做除法能够减小舍入误差的扩散,使得数值解比较可靠。而下面的图,则是经过若干步初等变化组成的上三角矩阵:

在组成上三角矩阵之后,就可以从下往上依次回代求出方程的解了。
#include
#include
#define MAX_MATRIX 10
/**
* @brief SwapRow 进行行交换
* @param m 待计算的矩阵
* row 待交行的行
* max_row 待交换的另一行
* n 矩阵行数
*/
static void SwapRow(double m[][MAX_MATRIX], int row, int max_row, int n) {
double swap;
for (int k = row; k <= n; k++) {
swap = m[row][k];
m[row][k] = m[max_row][k];
m[max_row][k] = swap;
}
}
/**
* @brief 组上三角矩阵
* @param m 待计算的矩阵
* n 矩阵行数
*/
static void SelectColE(double m[][MAX_MATRIX], int n) {
int max_row_e = 0; //主元所在行
double ratio = 0; //消元因数
for (int j = 0; j < n; j++) {
max_row_e = j;
for (int i = j; i < n; i++) {
if (fabs(m[i][j]) > fabs(m[max_row_e][j])) {
max_row_e = i;
}
}
if (max_row_e != j) {
SwapRow(m, j, max_row_e, n); //与最大主元所在行交换
}
//消元
for (int i = j + 1; i < n; i++) {
ratio = m[i][j] / m[j][j];
for (int k = j; k < n + 1; k++) {
m[i][k] -= m[j][k] * ratio;
}
}
}
}
/**
* @brief: Gauss 高斯列主元消元法求解线性方程(A*X = B)
* @param: m 由于A|B组成的增广矩阵,X为待求的解
* n 求解的元数,n要小于MAX_MATRIX
* @result:所求结果存放在m[][n]中
*/
void Gauss(double m[][MAX_MATRIX], int n) {
SelectColE(m, n); // 列选主元并消元成上三角
// 回代求解,结果存在m[][n]中
for(int i = n - 1; i >= 0; i--) {
for(int j = i + 1; j < n; j++) {
m[i][n] -= m[i][j] * m[j][n];
}
m[i][n] /= m[i][i];
}
}
double a[3][MAX_MATRIX] = {
{3,-1, 1, 4}, //A|B
{1, 1, 1, 6},
{2, 3,-1, 12}
};
int main(int argc ,char **argv) {
Gauss(a, 3);
printf("%f,%f,%f\r\n",a[0][3], a[1][3], a[2][3]);
return 0;
}
上述程序运行完成之后,终端输出:2.000000,3.000000,1.000000
代码参考链接:https://cloud.tencent.com/developer/article/1087352
这里的代码还不够完善,里面没有处理无解的情况,感兴趣的小伙伴可以继续完善它。
END