近期,我关注并学习了一个有趣方法,Feynman积分技巧。这个方法在某些方面可以替代复变函数在求取一些比较困难的定积分。 在这篇博文中,Panda博主通过两个例题展示了Feynman积分方法的强大和优美。 博文一开始引用了Feynman本文对该方法的评价, 这个方法是他的中学物理老师Bader先生给他的一本书中提到的, 展示了一种在积分符号内进行微分的特殊操作, 使用这种方法可以求解很多特定积分,为他在MIT赢得了很大的声誉, 这仅仅是由于自己的求解工具箱中多了这么一个特殊的手段。
博文中举得的第一个例子就这这个积分。

说实在的,这个积分看起来仿佛并不是那么困难 , 但经过尝试就会发现情况不是这样的。 对于通常的微积分技巧, 比如三角函数替换,变量替换,分部积分,将积分函数改成级数等,没有一个好使的。
接着Panda介绍了使用Feynman解决这个问题的要点。 把这个定积分看成参数alpha的函数, 然后确定在某些特殊的alpha下积分的值。比如alpha等于1时, 可以看到此时对应的定积分值为0。 接着对alpha进行求偏导数。 对结果再按照变量x求定积分。 注意,通常情况下,此时积分表达式中关于x积分就比较容易了。 然后对积分结果再对alpha求不定积分。实际上是求解关于alpha的微分方程的解。 使用前面确定alpha等于1时积分值作为边界条件,确定上述不定积分的常量。 最后便可以得到所求的积分数值了。 这里给出了求解的中间步骤。定义了alpha函数,f(α) 求出α等于1时的定积分,等于0。 然后再求f(α)对α的偏导数。
下面是第一个例题内容:求带有参数 的定积分:首先定义关于 的函数:
这里有两个积分需要进行求解。 对于α等于1时, 这个定积分为什么等于0呢? 网络上有很多证明都与这个积分有关系。 这里我们直接引用他们的积分结果。 原来的积分经过三角恒等变形, 可以最终拆分成这两项,再利用log,sin()的积分, 便可以得到f(1)等于0的结果了。 这是第一个定积分取值的求解。
第二个关于α的定积分就有点吓人了。 由于积分中没有了对数,所以可以直接使用基本积分技巧进行求取, 具体过程大家可以参照网络博文来看, 这里给出具体的求解结果。 这是f(α)的导数取值, 最后再根据f(1)的取值,可以得到f(α)的表达式, 这是最终求解结果。 虽然繁琐,但还是能够走得通的。

博文中第二个例子是求解一个定积分, 这是2005年普特曼数学竞赛中的一个题目, 这个比赛题目都非常困难,在120分的试卷中,平均分数还不到1分。
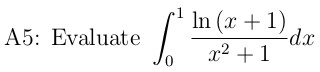
这个题目挺迷惑人的,就在于很多人以为可以使用常用的积分技巧进行求解,结果考试中浪费了大量的时间。 使用Feynman积分技巧才能够比较顺利的走得通。 首先引入变量a,将定积分的值定义成关于a的函数 I(a)。 然后求I(a)关于a的偏导数。 这样就将原来积分中的对数消掉了,剩下的部分就可以使用常见的积分技巧进行推导。 下面给出积分的结果。
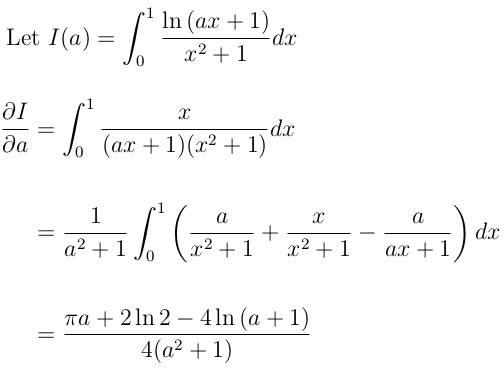
这是上述有理分式积分的结果。 然后在对上述结果进行定积分,求出I(a)的表达式, 这里似乎吧问题变得更糟了, 因为积分中的第二项仍然包含有对数部分, 但有趣的是,第二项的表达式实际上就是I(1) 这样就可以得到I(1)的表达式,它是一个有理分式的定积分。 下面再利用普通的有理分式积分方法, 就可以求出I(1)的取值,最终得到了原题的积分答案。
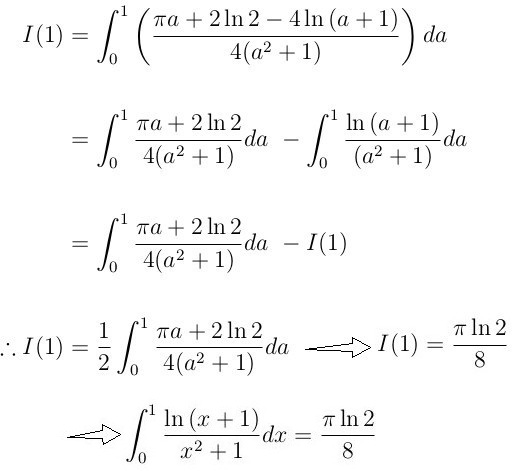
这里通过两个例子介绍了Feynman积分技巧, 博文作者最后总结到, 令人感到意外的是,很多场合解决一个一般性的问题反而比求解具体的问题实际更容易些。 作者同时也感到, 课外自学的重要性, 由于课内时间限制,很多时候,数学、科学等课程的教师没办法,无法将一些有趣的话题在课内展开。 这意味着如果你没有自学的主动性,就会与很多有趣、有用的知识擦肩而过了。 在当今信息爆炸的时代这一点尤其重要。 不过一开始作者提到Feynman掌握的积分技巧来自于他的高中老师的教导, 可见高中时期培养的求知欲望是多么的重要啊。
Richard Feynman’s Integral Trick: https://www.cantorsparadise.com/richard-feynmans-integral-trick-e7afae85e25c