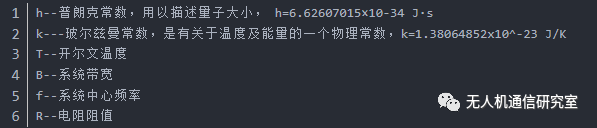
在无线通信计算接收灵敏度的时候,我们会用到-174dBm/Hz这个数字,他代表的意义究竟是什么呢?
【接收机三要素】 热噪声(称作kTB)+接收机系统噪声系数+从接受的信号中提取有用的信息所需的信噪比。接收机灵敏度定义了接收机可以接收到的并仍能正常工作的最低信号强度。灵敏度可用功率来表示,单位为dBm(通常是一个绝对值比较大的负dBm值),它也可以用场强来表示(mV/m)。
【接收灵敏度计算位置】虽然还没有统一规定,但把接收系统的灵敏度定义在接收天线的输出端口是常用的惯例。如果灵敏度定义在此点,在计算进入接收系统的信号功率时,接受天线的增益可以加到接收天线的信号功率上去。这就意味着 在计算接收系统灵敏度时,必须考虑连接天线和接收机用的电缆损耗和前置放大器以及功分器的影响。
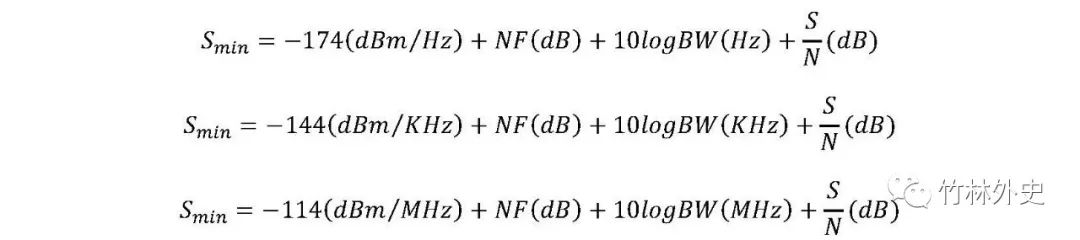

让我们从绝对零度说起。
在信号处理系统中,我们经常会听到噪声温度这个概念,而且噪声温度的量纲也是K(凯氏温度), 那噪声温度是什么意思呢?为什么会用温度来衡量噪声的大小?
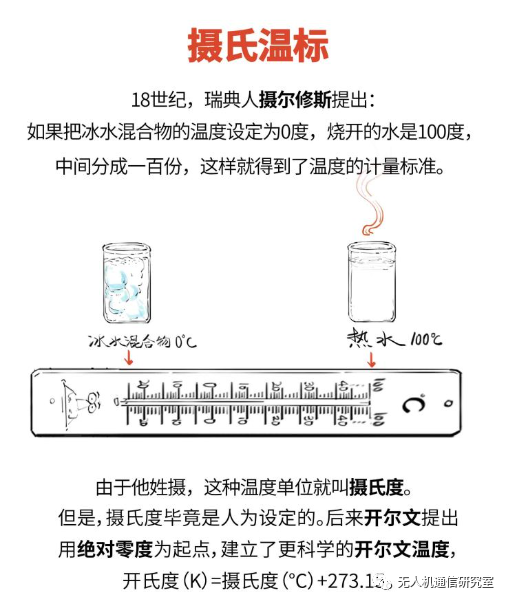
0K=-273.15℃
我们常说的绝对零度就是−273.15℃,即0K。

注意,此零度,是温度,不是无人机零度。
首先,要明确的一点是:噪声温度其实就是噪声功率的一种表示方法,至于为什么要用温度来表示功率大小?直接用功率不好么?
要解释噪声温度,就要从噪声说起。
根据噪声产生的机理,大致可以分为五大类:
(1)热噪声(Thermal Noise),
(2)散粒噪声(Shot Noise),
(3)闪烁噪声(Flicker Noise),
(4)等离子体噪声(Plasma Noise),
(5)量子噪声(Quantum Noise)。
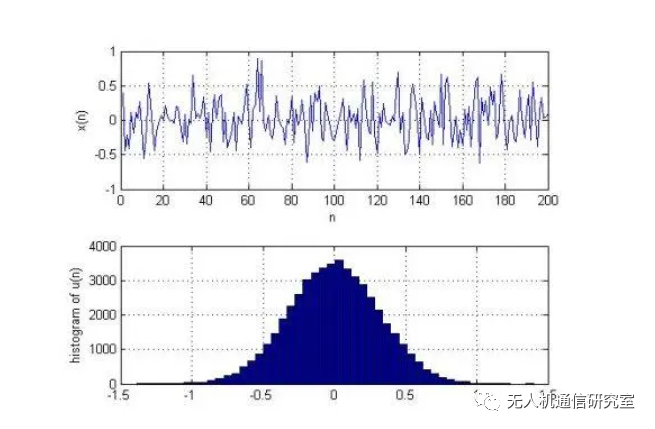
热噪声是最基本的一种噪声,可以说是无处不在的。热噪声又称为Johanson或Nyquist噪声,是由电子的热运动产生的。在绝对零度(0 K)以上,就会存在自由电子的热运动。因此,现实中的所有器件,都会产生热噪声。热噪声的功率谱密度不随频率变化,称为白噪声,又因服从Gauss概率密度分布,所以又称为高斯白噪声。
又是高斯,又是白噪声。
PDF地址:
https://wise.xmu.edu.cn/_data/2016/07/28/c6a3daf3_e3c2_49e3_9aad_bf95fa4446bf/%E6%AD%A3%E5%A4%AA%E5%88%86%E5%B8%83%20final.pdf
曲线:
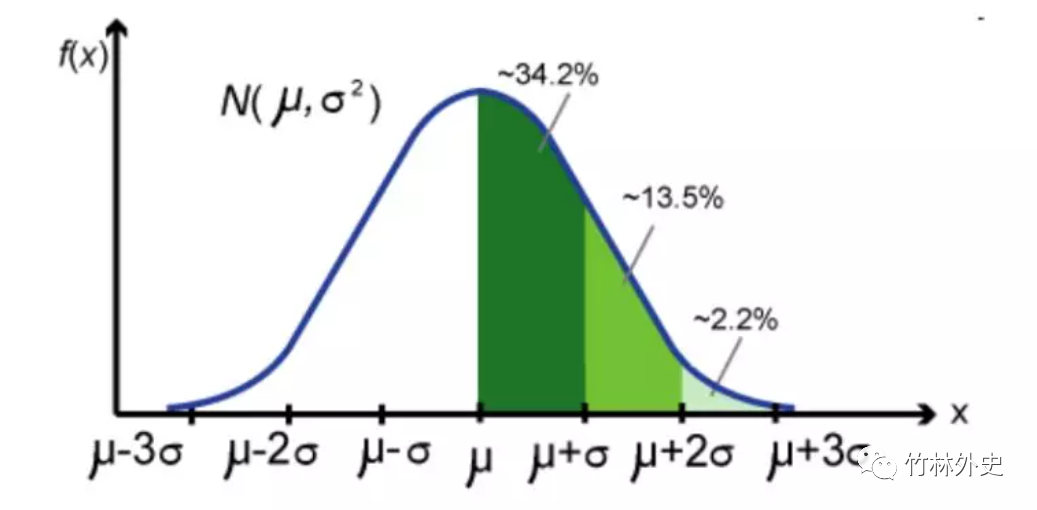
下面这几张图都很漂亮,凡尘都舍不得删除,可以帮助理解。宇宙热噪声。


将一个电阻置于温度为T (开尔文温度)的环境中,电阻中的自由电子随机运动,动能与温度T成正比。电子的随机运动会产生小的随机电压波动,此时电阻相当于一个噪声源。随机电压的有效值为

讲到这里,就得提一个关键的数字:-174dBm/Hz。什么意思呢?
在温度为290K,即16.85℃时,此时噪声的功率谱密度为:
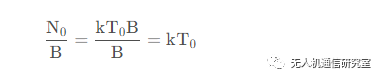
对该值取个dB对数

10∗log10(kT0)
=10∗log10(1.38064852∗10^23∗290)
=−203.98W/Hz
=−173.98dBm/Hz
≈−174dBm/Hz
因此,-174dBm/Hz是噪声的功率谱密度,当带宽为1Hz时,噪声功率为-174dBm,但噪声功率并不是噪底,因此很多人说-174dBm就是噪底这种说法其实是有问题的。
凡尘说:这里有个疑问,如果温度变化了呢?难道这个值也是变化么?
实际计算中,一般没有改变-174这个值对接收灵敏度的影响。
10∗log10(kT0)
=10∗log10(1.38064852∗(10^(-23))∗290)
=−203.98W/Hz
=−173.98dBm/Hz
≈−174dBm/Hz
注意,这里默认调用了:

10*log10为底的功率对数表
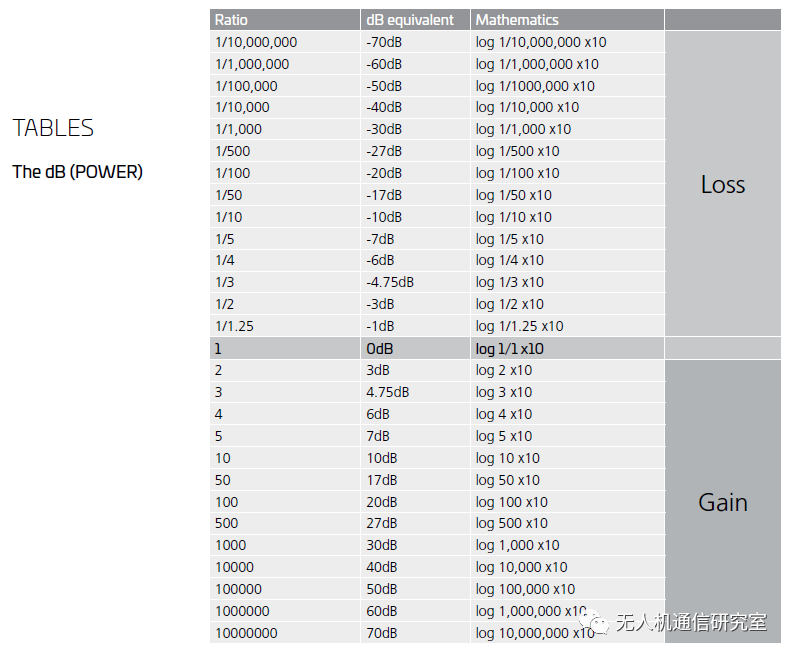
补充:
| ratio | dB | 增益或损耗 |
| 5/8 | -2 | 损耗 |
| 5/8*9/8=45/64 | -1.5 | 损耗 |
| 4/5 | -1 | 损耗 |
| 8/9 | -0.5 | 损耗 |
| 1 | 0 | |
| 9/8 | 0.5 | 增益 |
| 5/4 | 1 | 增益 |
| 8/5*8/9=64/45 | 1.5 | 增益 |
| 8/5 | 2 | 增益 |
以下为约数
(4/5)^6=0.25
(5/4)^6=4
(9/8)^2=5/4
(5/4)^2=8/5
如此
-1dB=10*log(4/5)
-6dB=6*10*log(4/5)=10*log((4/5)^6)
注意,此处是10*log10。
区别:在无线电磁波传输损耗模型中,是20*log10。
现在都有计算器,excel,matlab,这些技巧都几乎没有用武之地了。
但是,掌握一些简单运算的规律,在某些场景,简单分析问题,还是有一定帮助。
首先,对数的发明,是非常杰出的,非常大的程度上简化了对人脑和手工计算的能力要求。
16世纪末至17世纪初的时候,当时在自然科学领域(特别是天文学)的发展上经常遇到大量精密而又庞大的数值计算,于是数学家们为了寻求化简的计算方法而发明了对数.在数学史上,一般认为对数的发明者是十六世纪末到十七世纪初的苏格兰数学家——纳皮尔。 纳皮尔当时是一位天文爱好者,为了简化计算,他多年潜心研究大数字的计算技术,终于独立发明了对数。
具体,来,上数字。
首先,发射功率1w,是30dBm。
计算公式:
30dBm=10*log(1w/1mw)
这是基准。
所以,是相对1mw的对数值。dBm的m也是毫的意思。
继续,
0dBm=10*log(1mw/1mw)
这也是基准。
| 对数值 | 线性值 | 计算过程 |
| -100dBm | 100飞瓦 | 10*log(10^-13w/1mw) |
| -90dBm | 1皮瓦 | 10*log(10^-12w/1mw) |
| -60dBm | 1纳瓦 | 10*log(10^-9w/1mw) |
| -30dBm | 1微瓦 | 10*log(10^-6w/1mw) |
| -20dBm | 10微瓦 | 10*log(10^-5w/1mw) |
| -10dBm | 100微瓦 | 10*log(10^-4w/1mw) |
| 0dBm | 1毫瓦 | 10*log(10^-3w/1mw) |
| 10dBm | 10毫瓦 | 10*log(10^-2w/1mw) |
| 20dBm | 100毫瓦 | 10*log(10^-1w/1mw) |
| 30dBm | 1瓦 | 10*log(1w/1mw) |
| 33dBm | 2瓦 | 10*log(2*1w/1mw) |
| 35dBm | 3瓦 | 10*log(3*1w/1mw) |
| 37dBm | 5瓦 | 10*log(5*1w/1mw) |
| 40dBm | 10瓦 | 10*log(10*1w/1mw) |
| 43dBm | 20瓦 | 10*log(2*10*1w/1mw) |
| 46dBm | 40瓦 | 10*log(4*10*1w/1mw) |
| 50dBm | 100瓦 | 10*log(10*10*1w/1mw) |
其实,还有一个dBw的概念,其的基准是1w。整体比dBm大30。读者可以自行推导。
对数,真的是科学界有效的发明之一,极大地简化了人类的记忆负担和计算负担。

就像是阿拉伯数字,相对中文的数字一样。

中国古数学发展极慢,是不是和这个也有一定影响呢。
所以,这个数值其实是温度和噪声的折算关系。
一般,假定了大约17摄氏度为参考。
接上一次的疑问,那么,不同的温度,-174dBm/Hz还能用么?
口说无凭,直接算起。
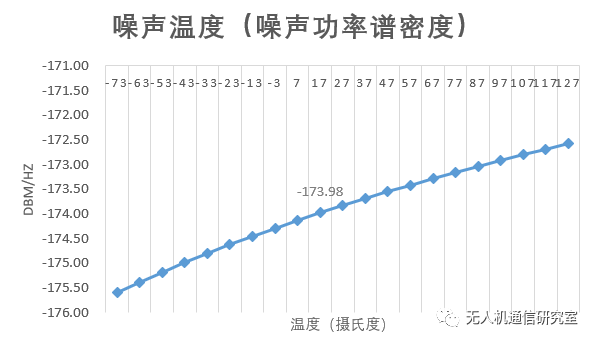
从上图可见,
(1)随着温度降低,噪声温度降低。所以,在低温下,通信接收机的性能会变好一些。
(2)大约从-73摄氏度到127摄氏度的范围,这个值变化了大约3dB。
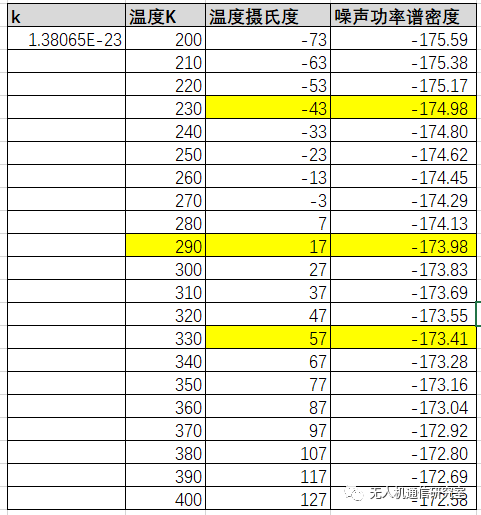
再看-40摄氏度,到+60摄氏度,那么,这个值大约变化了1.5dB。而相对17摄氏度,
(1)60摄氏度高温下,相对17摄氏度,恶化了0.5dB,
(2)低温下,相对17摄氏度,优化了1dB。
所以,一般用17摄氏度来代替整体的噪声温度,是相对合理的简化做法。
所以,在普通无人机的应用中,这些温度范围已经足够。
但是,我们想想卫星,是不是就有一种:

一天过冬夏,冰火两重天。
身临其境的感觉。
那么,公式中的290K是怎么来的?为什么是290k呢?
10∗log10(kT0)
=10∗log10(1.38064852∗(10^(-23))∗290)
=−203.98W/Hz
=−173.98dBm/Hz
≈−174dBm/Hz
1.第一种解释:
太阳表面温度6000K,
日地距离,
太阳半径。
即可计算得到这一模型下地球的平均温度约为290K,即17℃,在数量级上是正确的。
实际上地球的平均温度是15℃左右。
【凡尘说:所以,有时候是近似,但差别很小】
10∗log10(kT0)
=10∗log10(1.38064852∗(10^(-23))∗288)
=−204.01W/Hz
=−174.01dBm/Hz
也就是说,17摄氏度与15摄氏度,其噪声功率谱密度差为:
(−173.98)-(−174.01)=0.03
所以,几乎可以忽略不计。
1.1 计算过程
我们还可以用一个模型来粗略地估计地球表面的平均温度,为了让推导不会因为这里地方太小写不下,我们何不做一些离谱的假设:地球和太阳都是黑体,地球能吸收所有太阳传播到地球表面的辐射,地球向外发出辐射时不会受到大气等产生的阻碍,地球是一个理想的导热物体,即地球各部分的温度时刻保持一致。
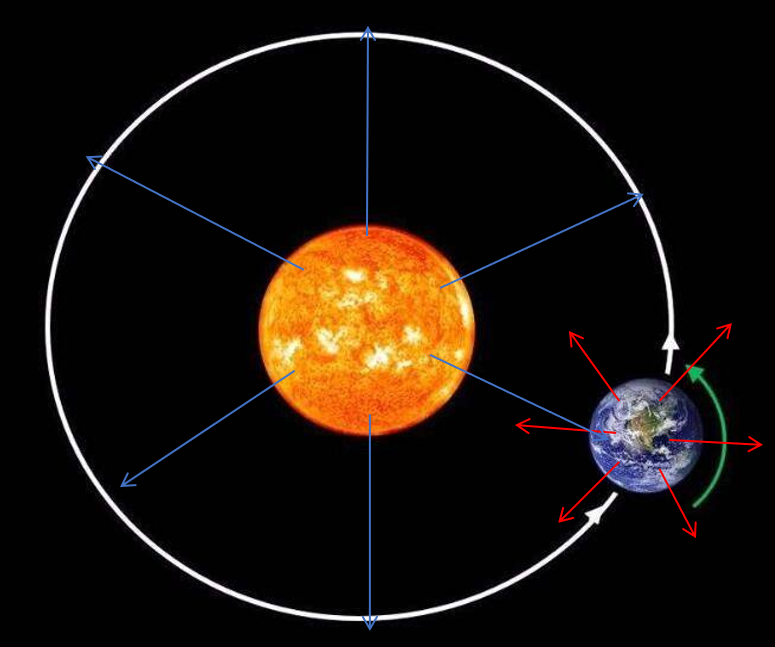
下面我们开始推导,注意到,太阳辐射的能量并不是全部都能够到达地球,因为假设太阳均匀地辐射,那么辐射到达日地距离时是均匀分布在一个半径为的球面上的,而地球在这一球面上只有小小的面积
(对数值的补充说明,不感兴趣的话可以跳过:这一面积不是地球被太阳照亮部分的表面积,因为我们要算功率,应该取垂直于太阳光的截面面积),
这部分面积上的太阳辐射应等于地球向外的辐射,即。
根据热辐射的规律,黑体单位面积辐射的热功率正比于绝对温度(注:即摄氏度加上273.15)的四次方,于是上式化为。
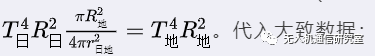
2.第二种解释:
为实现比较标准化,噪声因子在290K的标准温度下进行测量,选择这一温度值主要是依据哈拉尔·弗里斯 (Harald Friis) 于20世纪30年代在贝尔电话实验室开展的开创性研究结果。
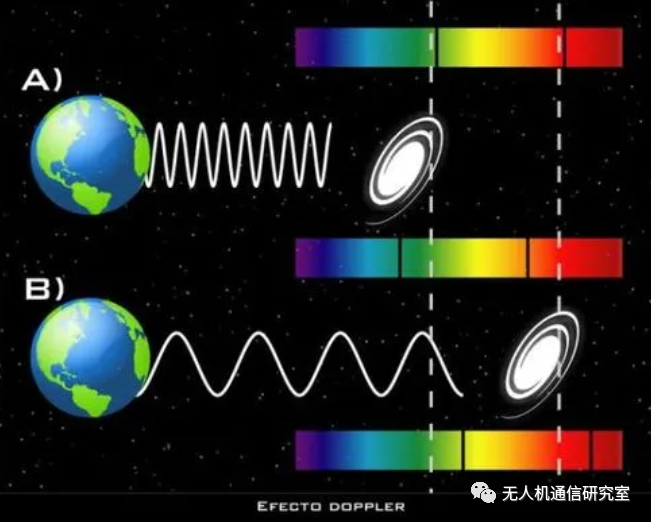
凡尘:第一次看到三棱镜,觉得神奇。原来宇宙是那么奇妙。

而如今,又学习到了电磁的噪声,竟然与温度相关。
初想起来觉得不可思议.
仔细想想,其实也对,这宇宙里的运动,不就是应该会产生能量向外传播的么,运动不就是会产生热噪声么。
在道理上,宇宙和人是一样的。

原来,物理学,是相通的,电磁学和宇宙天文学,产生了奇妙的联系。