它们具有以下特点:可用性、数据完整性、保密性、真实性和不可否认性。在第二节中,我们将详细分析这五种可能的漏洞点。在第三节中,将提出对这些问题的一些可能的解决方案,并对车内和车外通信进行区分。关于第二个问题,将遵循两个主要框架内提出的选择:5G和V2X(车连接一切)技术。第四节专门强调了两个框架中的单钥和双钥密码系统的区别。第五节讨论了一种特殊的风险,只要量子计算机有望被实际应用,这种风险就会增加。量子对抗措施被认为是不方便的,除了在安全密匙分配的特殊功能和非常昂贵的应用中。相反,基于纠错码的双密钥密码系统可能会引起一些兴趣。这个话题将在第六节中讨论,特别关注5G标准中已经提出的编码系列,即LDPC编码。最后,在第七节中得出结论。
不可否认性是一种属性,确保任何授权节点都对它引入到网络中的所有消息负责。换句话说,它不能否认这些信息的真实性。不可否认性是签署消息的一种义务,可以通过类似于身份验证所采用的双密钥加密来提供。机器对机器对话所基于的信任概念隐含着不可否认性规则。
III.5G框架和V2X框架
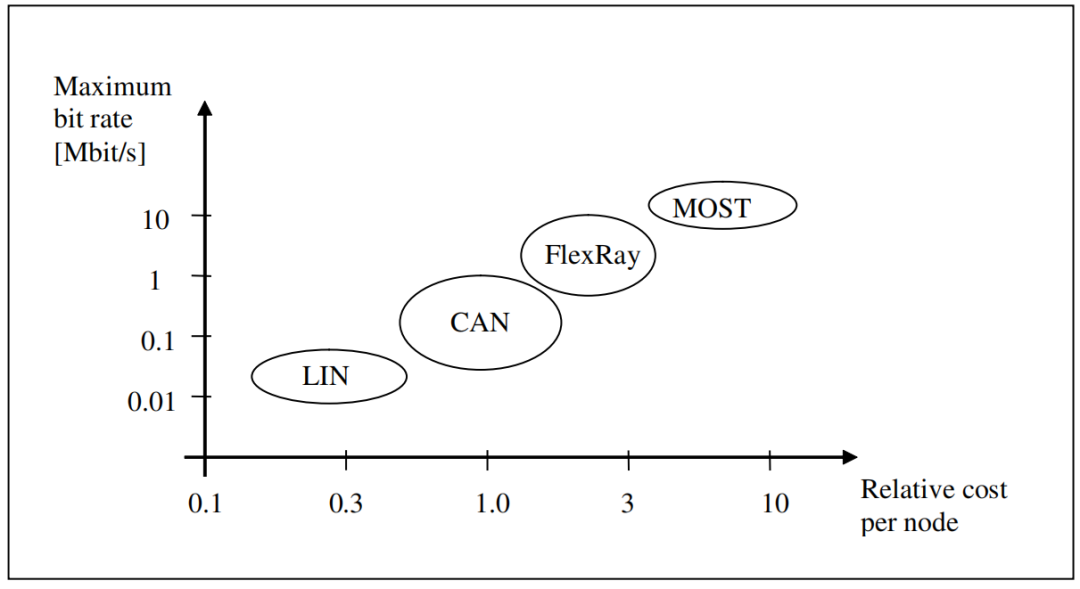
除了这种情况,可以认为对车内连接的攻击远不如对车外连接的攻击更有可能,因为车外连接必须有远距离无线电通信的支持。
IV.5G和V2X中的数据加密
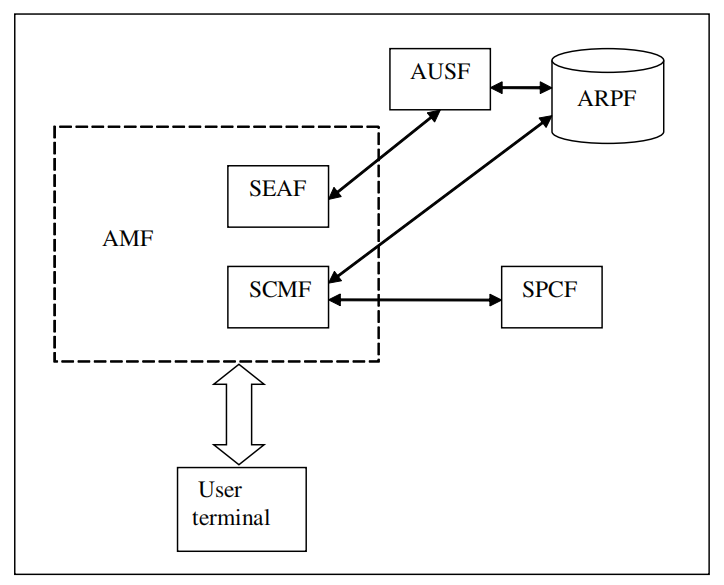
任何攻击都需要付出代价,这种代价与破解网络网络安全保护所需程序的复杂性成正比增加。在许多情况下,这种成本太高了。然而,当造成的损害或减去的数据的重要性很大时,这种成本是可以容忍的。如果攻击者由量子计算机提供,这种情况可能会发生,因为量子计算机在强制执行双键非对称密码系统方面具有极大的效率。粗略地说,非对称密码系统,如RSA,是基于两个大素数的乘积。攻击者使用传统计算机和暴力从乘积中提取两个素数因子的过程的复杂性可以用一个非多项式时间来估计。考虑到两个素数的实体(与密码系统中采用的私钥和公钥的长度有关),这一事实到现在为止已经阻止了许多攻击。众所周知,由Shor提出的一种算法,在量子计算机上实现,能够以多项式时间衡量的复杂度进行上述因式分解。这意味着,所有的非对称密码系统都有可能受到量子计算机的攻击。
V.量子计算机和量子通信
(量子密钥分配)

VI.后量子密码系统和
特定纠错码的使用

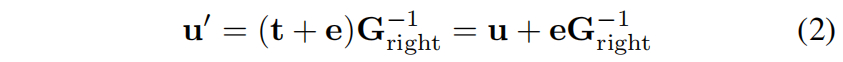
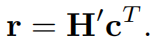
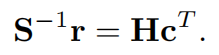
准循环LDPC码系列,大大减少了公钥的长度。LDPC码已经出现在随机纠错的实际标准中,这表明在未来可能的标准版本中,同一代码的部分纠错能力也被用于安排一个基于代码的密码系统,以保证双密钥的非对称加密,能够对比可能的量子计算机攻击。
VII.总结
在针对任何类型的网络攻击的汽车安全保障的可能解决方案的情况下,全面采用双密钥密码系统是可取的。经典算法,如RSA,面临着量子计算在大量因数分解为质数时的超高效率带来的风险。应该考虑后量子密码系统,以保护世界各地的大量用户,保持可接受的成本。在这方面,结合使用LDPC码所提供的纠错能力和数据保护可能是一个有吸引力的选择。一个有待解决的问题是与公共密钥的长度有关。采用结构化的奇偶校验矩阵,就像准循环LDPC码中出现的那样,可能是达到明显减少这一长度的最有效的途径。
参考文献:
[1] M. Di Natale, “Scheduling the CAN bus with earliest deadline techniques,” in Proceedings 21st IEEE Real-Time Systems Symposium, 2000, pp. 259–268.
[2] M. Wolf, A. Weimerskirch, and C. Paar, “Secure in-vehicle communication,” in Lemke K., Paar C., Wolf M. (eds) Embedded Security in Cars. Berlin, Heidelberg: Springer-Verlag, 2006.
[3] M. Syafrudin, G. Alfian, N. Fitriyani, and J. Rhee, “Performance analysis of IoT-based sensor, big data processing, and machine learning model for real-time monitoring system in automotive manufacturing,” Sensors, vol. 18, p. 2946, Sep. 2018.
[4] C. A. Kerrache, C. T. Calafate, J. Cano, N. Lagraa, and P. Manzoni, “Trust management for vehicular networks: An adversary-oriented overview,” IEEE Access, vol. 4, pp. 9293–9307, 2016.
[5] S. Chandra, S. Paira, S. S. Alam, and G. Sanyal, “A comparative survey of symmetric and asymmetric key cryptography,” in 2014 International Conference on Electronics, Communication and Computational Engi- neering (ICECCE), 2014, pp. 83–93.
[6] K. Z. Ghafoor, M. Guizani, L. Kong, H. S. Maghdid, and K.F.Jasim, “Enabling efficient coexistence of DSRC and C-V2X in vehicular networks,” IEEE Wireless Communications, vol. 27, no. 2, pp. 134– 140,
2020.
[7] M. Scalas and G. Giacinto, “Automotive cybersecurity: Foundations for next-generation vehicles,” in 2019 2nd International Conference on new Trends in Computing Sciences (ICTCS), 2019, pp. 1–6.
[8] X. Zhang, A. Kunz, and S. Schröder, “Overview of 5G security in 3GPP,” in 2017 IEEE Conference on Standards for Communications and Networking (CSCN), 2017, pp. 181– 186.
[9] A. Alnasser, H. Sun, and J. Jiang, “Cyber security challenges and solutions for V2X communications: A survey,” Computer Networks, vol. 151, pp. 52 – 67, 2019.
[10] Xin Zhou and Xiaofei Tang, “Research and implementation of rsa algorithm for encryption and decryption,” in Proceedings of 2011 6th International Forum on Strategic Technology, vol. 2, 2011, pp. 1118–
1121.
[11] C. P. Schnorr, “Refined analysis and improvements on some factoring algorithms,” in Automata, Languages and Programming, S. Even and O. Kariv, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 1981, pp. 1– 15.
[12] P. W. Shor, “Algorithms for quantum computation: discrete logarithms and factoring,” in Proceedings 35th Annual Symposium on Foundations of Computer Science, 1994, pp. 124– 134.
[13] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed. USA: Cambridge
University Press, 2011.
[14] S. Ducci, L. Lanco, J. . Likforman, X. Marcadet, J. A. W. van Houwelingen, H. Zbinden, G. Leo, and V. Berger, “Counterpropagating twin photons in the telecom range: a narrow-bandwidth semiconductor source,” in 2007 European Conference on Lasers and Electro-Optics and the International Quantum Electronics Conference, 2007, pp. 1– 1.
[15] F. Karinou, H. H. Brunner, C. F. Fung, L. C. Comandar, S. Bettelli,D. Hillerkuss, M. Kuschnerov, S. Mikroulis, D. Wang, C. Xie, M. Peev, and A. Poppe, “Toward the integration of cv quantum key distribution in deployed optical networks,” IEEE Photonics Technology Letters, vol. 30, no. 7, pp. 650–653, 2018.
[16] D. Huang, Y. Zhao, T. Yang, S. Rahman, X. Yu, X. He, and J. Zhang,“Quantum key distribution over double-layer quantum satellite net- works,” IEEE Access, vol. 8, pp. 16 087– 16 098, 2020.
[17] J. A. Buchmann, D. Butin, F. Göpfert, and A. Petzoldt, “Post-quantum cryptography: State of the art,” in Ryan P., Naccache D., Quisquater JJ. (eds) The New Codebreakers, Lecture Notes in Computer Science, vol.9100. Springer-Verlag, 2016.
[18] G. Cancellieri, Polynomial Theory of Error Correcting Codes. Springer,2015.
[19] R. J. McEliece, “A public-key cryptosystem based on algebraic coding theory.” DSN Progress Report, pp. 114– 116, 1978.
[20] S. Ahn, K. Kim, S. Myung, S. Park, and K. Yang, “Comparison of low-density parity-check codes in ATSC 3.0 and 5G standards,” IEEE Transactions on Broadcasting, vol. 65, no. 3, pp. 489–495, 2019.
[21] H. Niederreiter, “Knapsack-type cryptosystems and algebraic coding theory,” Probl. Contr. and Inform. Theory, vol. 15, pp. 159– 166, 1986.
[22] P. Santini, M. Battaglioni, M. Baldi, and F. Chiaraluce, “Hard-decision iterative decoding of LDPC codes with bounded error rate,” in ICC 2019 - 2019 IEEE International Conference on Communications (ICC), 2019, pp. 1–6.
[23] ——, “Analysis of the error correction capability of LDPC and MDPC codes under parallel bit-flipping decoding and application to cryptogra- phy,” IEEE Transactions on Communications, 2020.
分享不易,恳请点个【👍】和【在看】