点击上方蓝字关注我们
周六锁定“温温故,知知新”,获取我司技术知识速递——您发挥才能,我们提供工具!别忘了参与文末有奖活动哦!
本篇文章节选自国际知名电源专家Christophe Basso所著的《开关转换器动态分析采用快速分析技术》,本篇文章是此次系列文章的最终篇。在下一期的系列文章中,我们将聚焦考量运算放大器在Type-2补偿器中的动态响应,欢迎大家持续关注~
开关转换器动态分析采用快速分析技术(最终篇)
作者简介
Christophe Basso
安森美半导体法国图卢兹 Technical Fellow
他拥有超过20年的电子电路设计经验,在电力电子转换领域拥有近30项专利,他原创了许多集成电路芯片,其中代表性为 NCP120X 系列,它重新定义了电源低待机功耗设标准。
Christophe Basso出版了多部著作,《开关模式 SPICE 仿真和实用设计》深受广大工程师的欢迎并二次改版,《为线性和开关电源设计控制回路:教程指南》为工程师设计补偿和环路稳定性提供了实用指南,《线性电路传递函数:介绍快速分析技术》以说教的方式,为学生和需要强大的工具以快速分析日常工作中的复杂电子电路的工程师提供对电路分析的不同角度。
开关转换器动态分析采用快速分析技术 第二篇
06
二阶系数
对于二阶系数,我们将设置电容C2处于其高频状态(以短路代替它),同时我们将确定驱动电感L1的阻抗。
图17说明了这种方法。因为输出因C2短路,节点a和c都处于相同的0V电势。电路简化为右侧示意图。
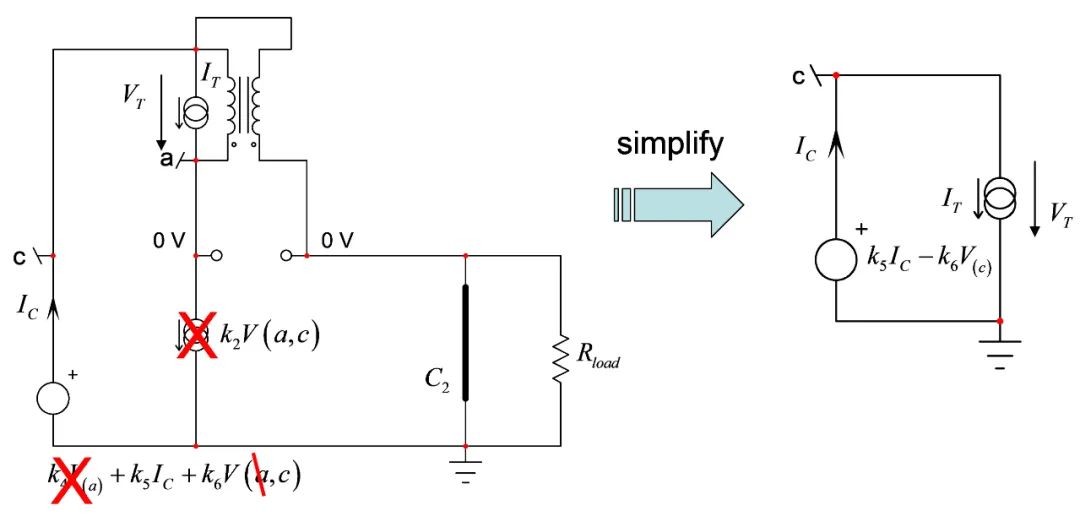
图十七
点击查看大图 △
图17:二阶系数设置储能元件之一处于其高频状态(C2),同时您可确定电感两端的电阻。
我们可写出描述VT电压的第一个方程。观察到a) IT和IC是相同的,b) VT = –V(c),我们有
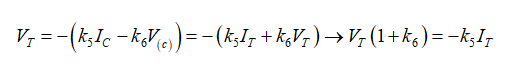
(34)
因式分解VT/IT,L1两端的阻抗为
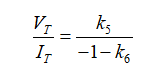
(35)
二阶时间常数定义为
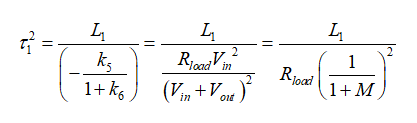
(36)
如果我们认为Vout = MVin,b2系数表示为
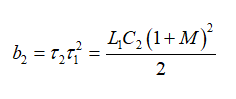
(37)
合并我们确定的时间常数,得出分母D(s)
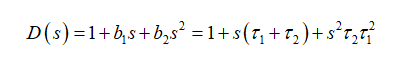
(38)
如果我们考虑一个低Q值的近似值,这二阶分母可以近似由两级联极点定义为
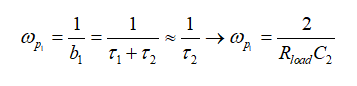
(39)
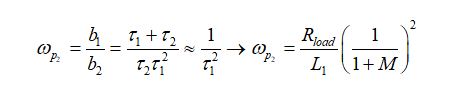
(40)
和合并为
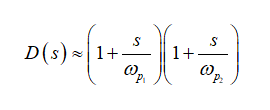
(41)
07
零点的确定
如上文所述,当激励源调至零角频率sz,,变形电路的响应为无信号输出(见图1)。该运用现将包括将激励源复原和确定无信号输出的变形电路的条件。图18所示为我们需要研究的更新电路。无信号输出的有趣之处在于其传播至其它节点。
例如,如果Vout = 0V,然后由于变压器高边连接,节点a也处于0 V,所有涉及该节点的表达式可以简化为如图所示。如果输出无信号,则电流I1也为零,这意味着Ic=I3。
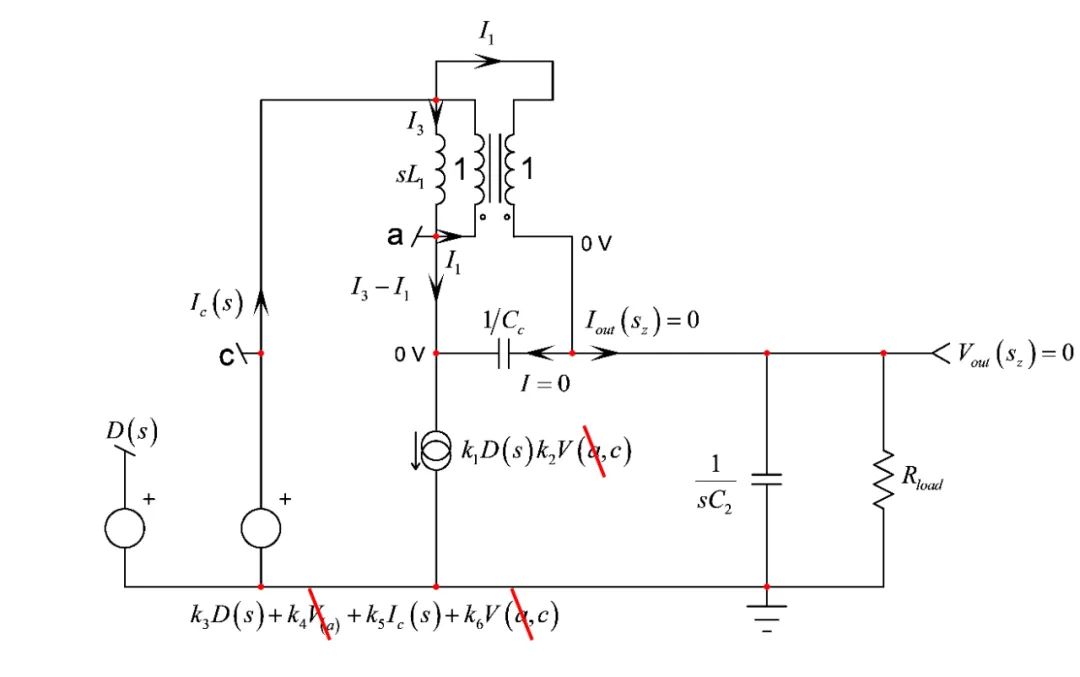
图十八
点击查看大图 △
图18:在s=sz的特定条件下,观察变形的电路,无信号响应。
节点c的电压定义为
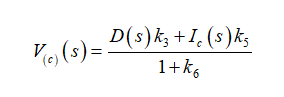
(42)
因此,电流Ic等于节点c的电压除以L1的阻抗。
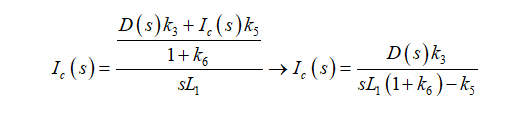
(43)
而电流等于
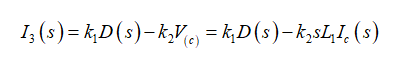
(44)
现将(43)代入(44),然后视Ic=I3:
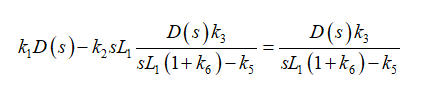
(45)
求解s,将系数k的值换为它们在图13中的值,重新整理,您会发现
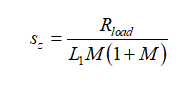
(46)
这是个正的根源,因此为右半平面零点。通过收集所有的部分,发现极点和零点实际上是一个DCM buck-boost转换器的极点和零点而得出完整的传递函数:
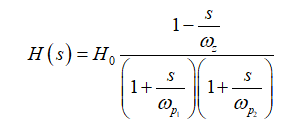
(47)
及
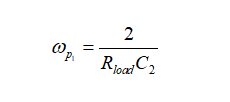
(48)
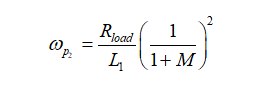
(49)
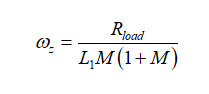
(50)
和
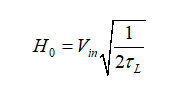
(51)
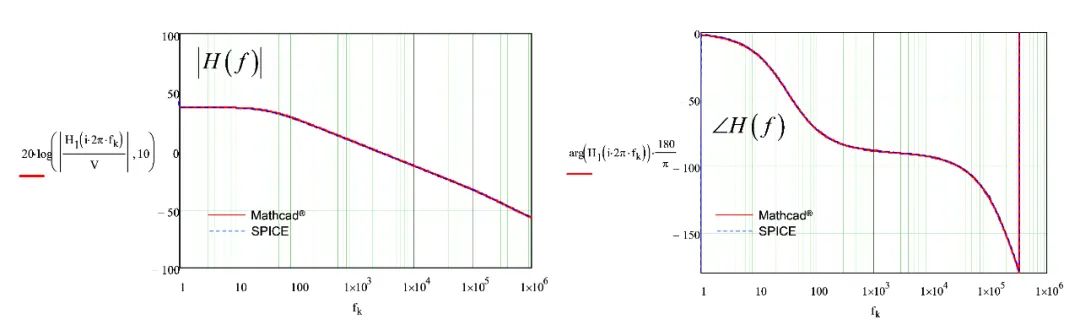
最后的检查,我们可比较Mathcad®和图11大信号模型的SPICE仿真的动态响应。如图19所示,曲线完美重合。
图十九
点击查看大图 △
图19:Mathcad®和SPICE提供完全相同的响应(曲线完美叠加)。
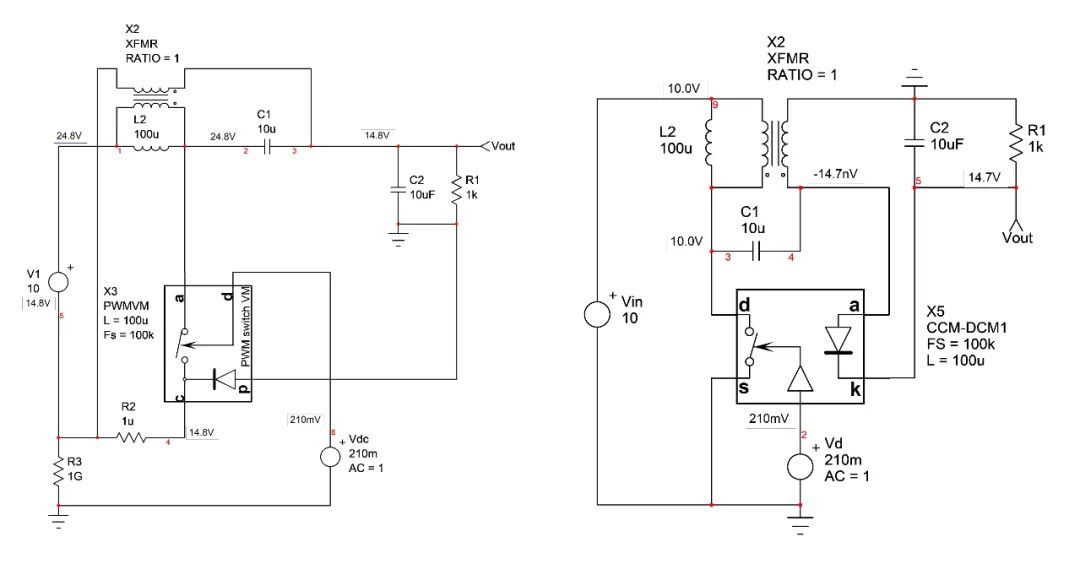
另一个验证是由采用不同的平均模型(架构如[11])仿真相同的SEPIC结构构建。这也是一个自动切换的CCM-DCM模型,但走线方式稍有不同。图20所示为两种平均模型采用一个类似的SEPIC架构。
图二十
点击查看大图 △
图20:CoPEC平均模型包括单独的开关和二极管连接。
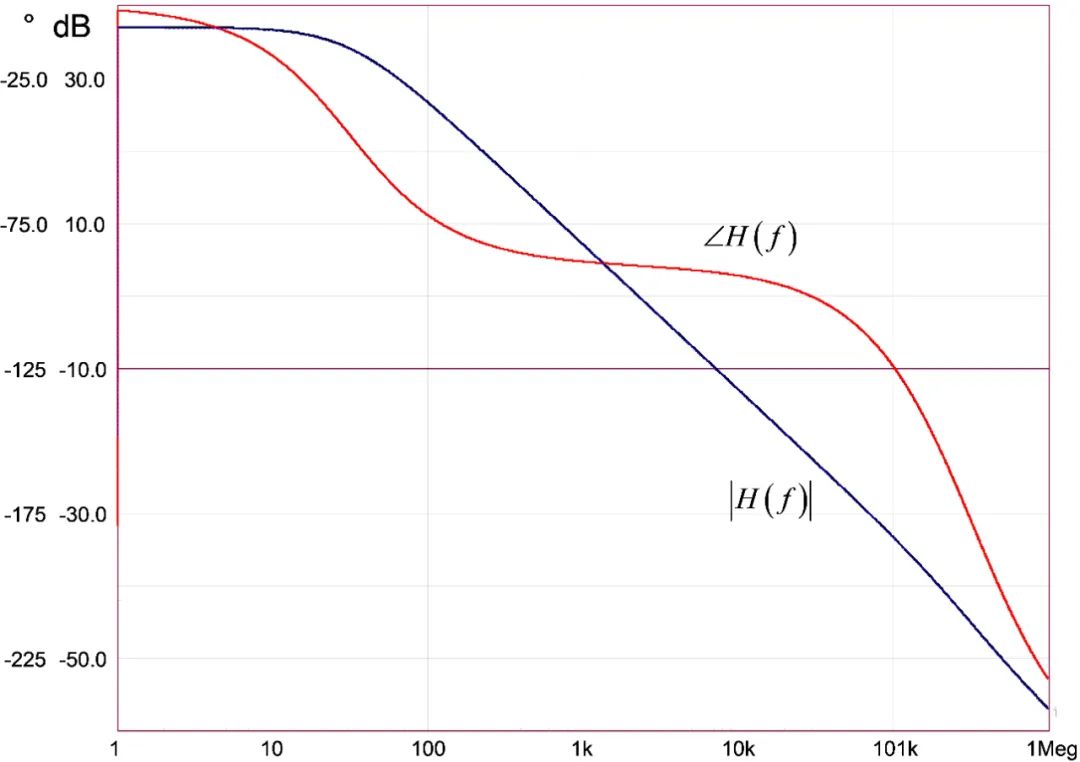
图21证实了两个交流响应在相位和幅值上完全相同。
图二十一
图21:DCM PWM开关和CoPEC DCM模型提供相同的动态响应。
08
总结
快速分析技术为推导线性电路传递函数提供了一种快速而高效的方法。在无源电路中,观察是可能的,而且是经常的,无需写一行代数就能得到传递函数。随着电路变得复杂和包括激励源,您不得不采用经典的KCL和KVL分析。但当您确定分子和分母中个别的多项式因子时,很容易跟踪错误和只关注错误项,如果有的话。在复杂的电路中,小草图和SPICE的帮助是极有用的。
最后,最终结果以一种有意义的格式表示,并可直接识别出极点和零点位于何处。这是非常重要的,因为您必须知道问题隐藏在传递函数的何处。作为一个设计人员,您必须平衡它们,这样自然的产生传播或组件的变化不会危及您的系统在运行中的稳定性。

