Q值的基本定义,如下图公式所示:

电感和电容的Q值
理想的电容,不耗散能量,Q值为无穷大,但是如果考虑级联寄生电阻,则
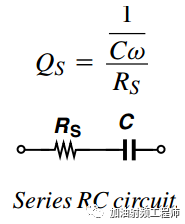
如果以并联电容来模拟电容的损耗的话,则
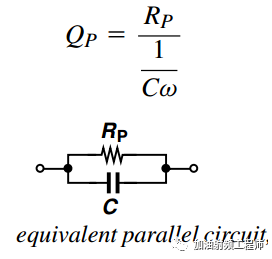
同样,和电容类似,电感的等效电路可有串联和并联两种形式。

谐振器的Q值
看一下有耗电感和有耗电容组成的并联谐振电路的Q值。
在一个相对较窄的频率范围内,有耗电感和有耗电容都可以用一个并联电阻来模拟其寄生电阻。
如下图所示:

其中,电感和电容的Q值分别为:
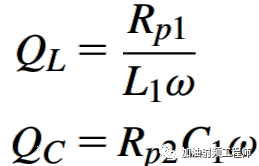
当谐振器处于谐振状态时:
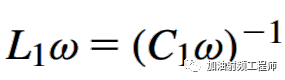
整个谐振器的Q值为:
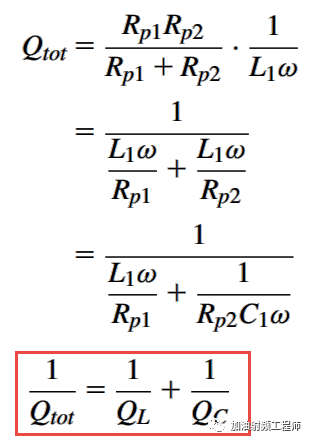
由上面的式子可知,电感和电容的Q值越高,其组成的并联谐振器的Q值也越高
振荡器的Q值
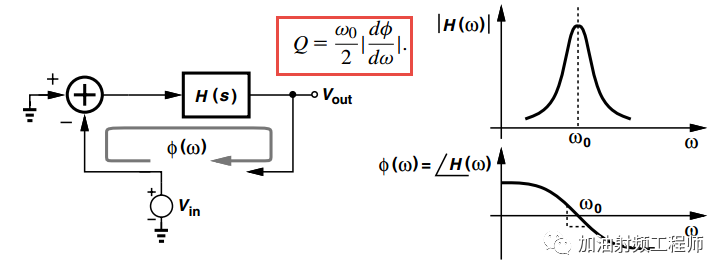
适合振荡器的Q值定义,如下图所示。电路被看成一个反馈系统, φ(ω)为开环传递函数的相位,w0为谐振频率。开环Q值的定义如下图红框所示。
以一个交叉耦合LC振荡器为例,计算其开环Q值。
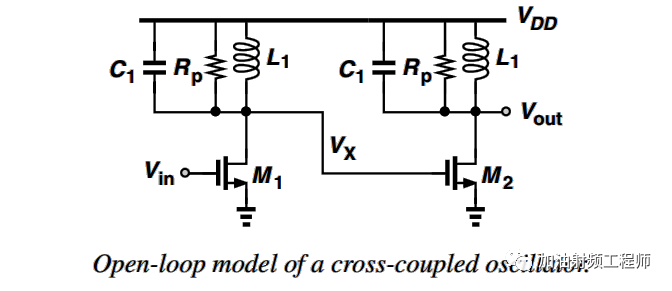

上述推导中,Qtank为每一级中谐振器的Q值。这个结果表面,级联后的电路比单独一级具有更高的Q值。
也就是说,振荡器的Q值,和谐振器的Q值直接相关。
振荡器的Q值和相噪的关系
把振荡器看成线性时不变系统,对其相位进行分析。此模型称为Leeson's model。
可以从振荡器的线性小信号模型出发,基本思路是将相位噪声解释为由振荡器内部热噪声通过振荡器环路转换产生的,在输出表现为相位噪声。
用如下图所示的正反馈模型来等效振荡器,把等效噪声源接在此系统的输入端,以此来对这个等效线性小信号模型进行噪声分析。
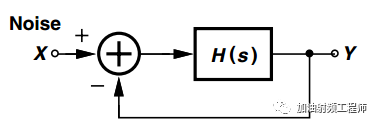
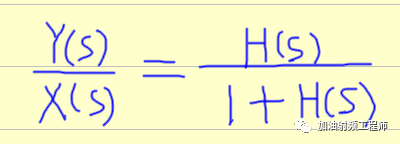
根据巴克豪森判据,当振荡器处于稳定状态时,在振荡频率处, H( jω0)=-1。
在振荡频率附近,比如 ω= ω0 + Δω处,可以对H(jw)进行泰勒展开近似。
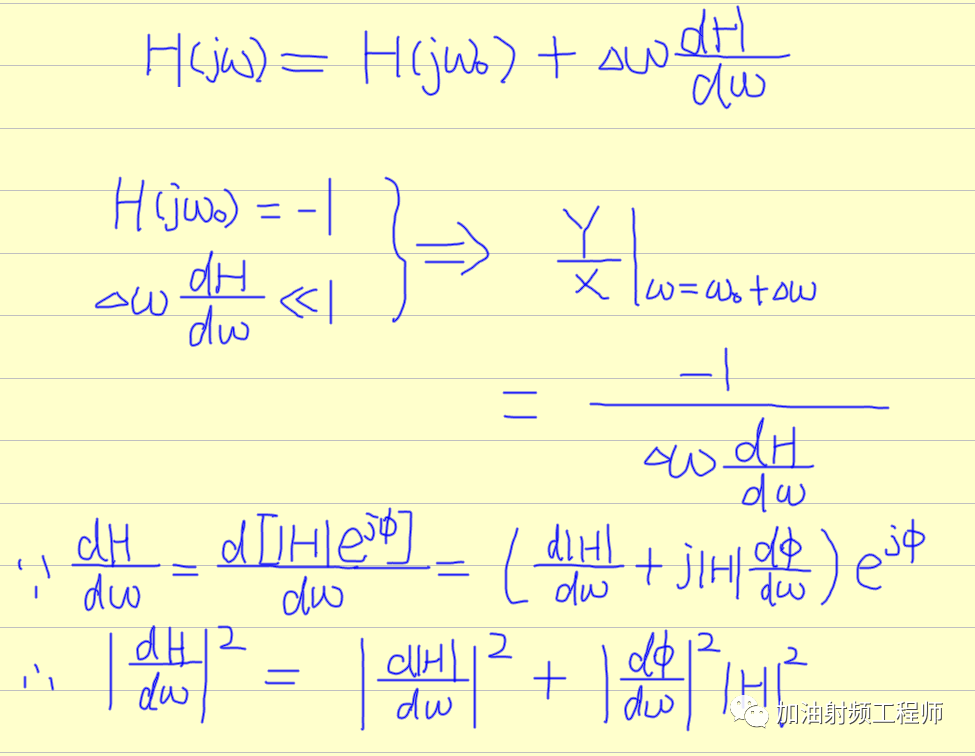
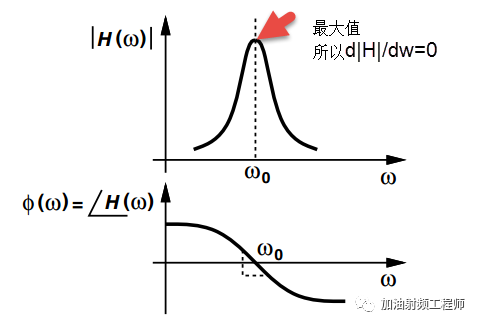
因为当振荡器处于稳定状态时,|H(w)|=1;且在振荡频率附近H(w)幅值最大,如下图所示,所以幅值变化率为0.
因此,
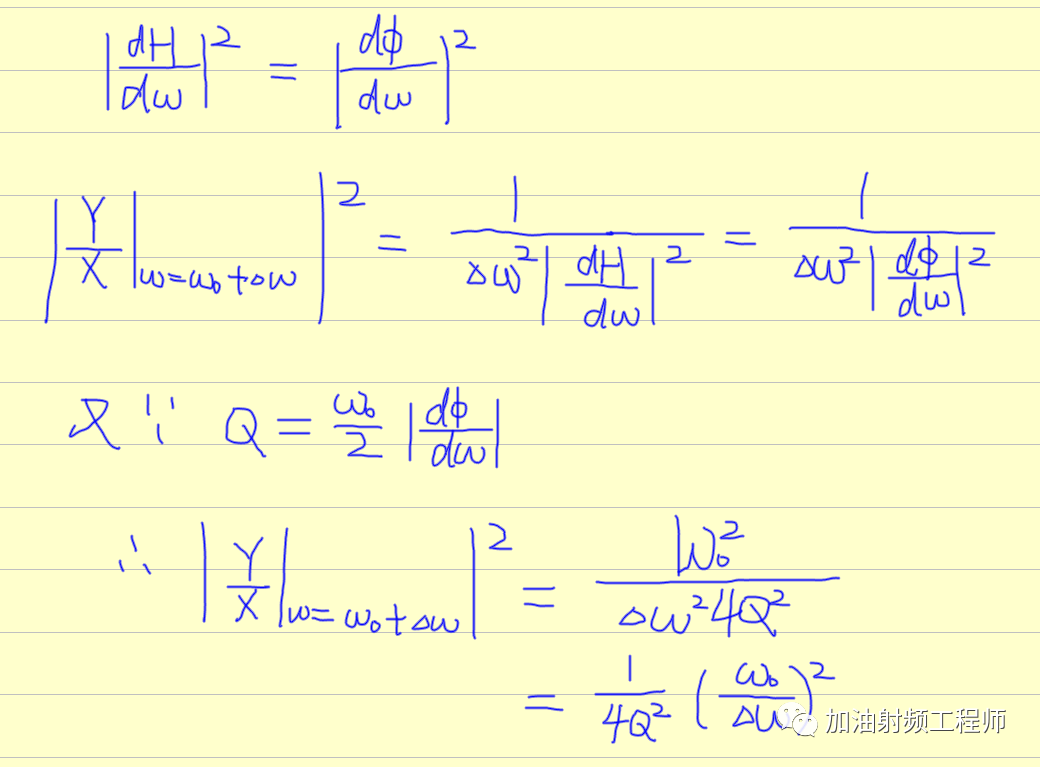
如果只考虑谐振器等效并联电阻来等效振荡器内的热噪声,即X=4KTR, 并假设一般噪声能量变为相位噪声,另一半为幅度噪声,因此输出端输出Y即为振荡器的输出噪声。
所以:
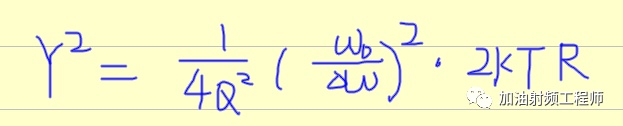
因为相位噪声是噪声相对于信号的噪声信号比,因而相位噪声为:
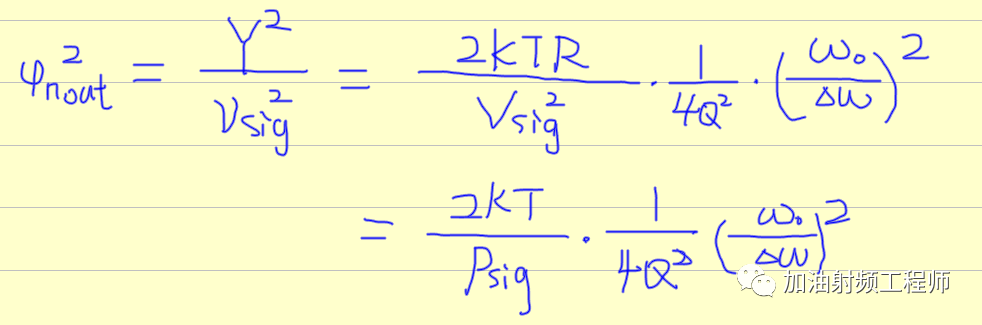
上述等式即是初步的只考虑简单热噪声的Leeson's模型。可以看到相位噪声和振荡频率成正比,与Q值,偏差频率以及信号功率成正比。
所以,当电感电容的Q值大==》谐振器的Q值==》振荡器的Q值==》相位噪声小。
文献:
razavi,射频微电子
张刚,CMOS集成锁相环电路设计