在编程大佬眼中，线性代数到底是什么样的？

在大学数学学科中，线性代数是最为抽象的一门课，从初等数学到线性代数的思维跨度比微积分和概率统计要大得多。很多人学过以后一直停留在知其然不知 其所以然的阶段，若干年之后接触图形编程或机器学习等领域才发现线性代数的应用无处不在，但又苦于不能很好地理解和掌握。的确，多数人很容易理解初等数学 的各种概念，函数、方程、数列一切都那么的自然，但是一进入线性代数的世界就好像来到了另一个陌生的世界，在各种奇怪的符号和运算里迷失了。

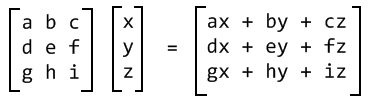
我在初接触线性代数的时候简直感觉这是一门天外飞仙的学科，一个疑问在我脑子里浮现出来：

线性代数到底是一种客观的自然规律还是人为的设计？

如果看到这个问题，你的反应是“这还用问，数学当然是客观的自然规律了”，我一点儿都不觉得奇怪，我自己也曾这样认为。从中学的初等数学和初等物理 一路走来，很少人去怀疑一门数学学科是不是自然规律，当我学习微积分、概率统计时也从来没有怀疑过，唯独线性代数让我产生了怀疑，因为它的各种符号和运算 规则太抽象太奇怪，完全对应不到生活经验。所以，我还真要感谢线性代数，它引发了我去思考一门数学学科的本质。其实，不止是学生，包括很多数学老师都不清 楚线性代数到底是什么、有什么用，不仅国内如此，在国外也是这样，国内的孟岩写过《理解矩阵》，国外的Sheldon Axler教授写过《线性代数应该这样学》，但都还没有从根本上讲清楚线性代数的来龙去脉。对于我自己来讲，读大学的时候没有学懂线性代数，反而是后来从编程的角度理解了它。很多人说数学好可以帮助编程，我恰好反过来了，对程序的理解帮助了我理解数学。

本文的目标读者是程序员，下面我就带各位做一次程序员在线性代数世界的深度历险！既然是程序员，在进入线性代数的领域之前，我们不妨先从考察一番程序世界，请思考这样一个问题：

计算机里面有汇编、C/C++、Java、Python等通用语言，还有Makefile、CSS、SQL等DSL，这些语言是一种客观的自然规律还是人为的设计呢？

为什么要问这样一个看起来很蠢的问题呢？因为它的答案显而易见，大家对天天使用的程序语言的认识一定胜过抽象的线性代数，很显然程序语言虽然包含了 内在的逻辑，但它们本质上都是人为的设计。所有程序语言的共同性在于：建立了一套模型，定义了一套语法，并将每种语法映射到特定的语义。程序员和语言实现 者之间遵守语言契约：程序员保证代码符合语言的语法，编译器/解释器保证代码执行的结果符合语法相应的语义。比如，C++规定用new A()语法在堆上构造对象A，你这样写了C++就必须保证相应的执行效果，在堆上分配内存并调用A的构造函数，否则就是编译器违背语言契约。

从应用的角度，我们能不能把线性代数视为一门程序语言呢？答案是肯定的，我们可以用语言契约作为标准来试试。假设你有一个图像，你想把它旋转60 度，再沿x轴方向拉伸2倍；线性代数告诉你，“行！你按我的语法构造一个矩阵，再按矩阵乘法规则去乘你的图像，我保证结果就是你想要的”。

实际上，线性代数和SQL这样的DSL非常相似，下面来作一些类比：

• 模型和语义：SQL是在低级语言之上建立了关系模型，核心语义是关系和关系运算；线性代数在初等数学之上建立了向量模型，核心语义是向量和线性变换

• 
  

• 语法：SQL为每种语义定义了相应的语法，如select, where, join等；线性代数也定义了向量、矩阵、矩阵乘法等语义概念相应的语法

• 
  

• 编译/解释：SQL可以被编译/解释为C语言；线性代数相关概念和运算规则可以由初等数学知识来解释

• 
  

• 实现：我们可以在MySQL、Oracle等关系数据库上进行SQL编程；我们也可以在MATLAB、Mathematica等数学软件上进行线性代数编程

所以，从应用的角度看，线性代数是一种人为设计的领域特定语言(DSL)，它建立了一套模型并通过符号系统完成语法和语义的映射。实际上，向量、矩阵、运算规则的语法和语义都是人为的设计，这和一门语言中的各种概念性质相同，它是一种创造，但是前提是必须满足语言契约。

可能有人对把线性代数当成一门DSL不放心，我给你一个矩阵，你就把我的图形旋转了60度沿x轴拉伸了2倍，我总感觉不踏实啊，我都不知道你“底 层”是怎么做！其实，这就像有的程序员用高级语言不踏实，觉得底层才是程序的本质，老是想知道这句话编译成汇编是什么样？那个操作又分配了多少内存？别人 在Shell里直接敲一个wget命令就能取下一个网页，他非要用C语言花几十分钟来写一堆代码才踏实。其实，所谓底层和上层只是一种习惯性的说法，并不 是谁比谁更本质。程序的编译和解释本质上是不同模型间的语义映射，通常情况下是高级语言映射为低级语言，但是完全也可以把方向反过来。Fabrice Bellard用JavaScript写了一个虚拟机，把Linux跑在JavaScript虚拟机上，这就是把机器模型往JavaScript模型上映射。

建立新模型肯定依赖于现有的模型，但这是建模的手段而不是目的，任何一种新模型的目的都为了更简单地分析和解决某一类问题。线性代数在建立的时候，它的各种概念和运算规则依赖于初等数学的知识，但是一旦建立起来这层抽象模型之后，我们就应该习惯于直接利用高层次的抽象模型去分析和解决问题。

说到线性代数是为了比初等数学更容易地分析和解决问题，下面我们通过一个例子来实际感受一下它的好处：

给定三角形的顶点(x1, y1), (x2, y2), (x3, y3)，求三角形的面积。

初等数学中三角形面积最著名的计算公式是area = 1/2 * base * height ，当三角形有一条边恰好在坐标轴上时我们就很容易算出它的面积。但是，假如同样一个三角形我们把坐标轴旋转一下，让它的边不在坐标轴上，怎么办？我们还能得到它的底和高吗？答案肯定是可以的，但是就明显复杂了，而且还要分很多种情况去分别讨论。

相反，如果我们用线性代数知识来解决这个问题就非常轻松。在线性代数中两个向量a，b的叉积(Cross Product)是一个向量，其方向与a，b垂直，其大小等于a，b构成的平行四边形的面积:

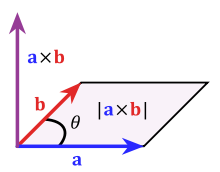
我们可以把三角形的边视为向量，所以三角形的面积等于两个边向量的叉积除以二的绝对值：

area = abs(1/2 * cross_product((x2 - x1, y2 - y1), (x3 - x1, y3 - y1)))

注：abs表示取绝对值，cross_product表示两个向量的叉积。

这样一个在初等数学里面有点儿小难的问题在线性代数中瞬间搞定！可能有人会说，你直接基于叉积来做，当然简单了，但是叉积本身不是也挺复杂的吗？你把它展开试试看呢？是的，模型的作用就是把一部分复杂性隐藏到模型中，使得模型的使用者可以更加简单地解决问题。曾经有人质疑C++太复杂，C++之父Bjarne Stroustrup这样回答：

Complexity will go somewhere: if not the language then the application code.

在特定环境下，问题的复杂性是由其本质决定的，C++把一部分的复杂性纳入了语言和标准库，目的是使得应用程序更为简单。当然，并非所有场合C++ 都使得问题更加简单，但是从原理上讲，C++的复杂性是有道理的。除了C++，Java、SQL、CSS等各种语言和框架莫不如是，想象一下，如果不使用 数据库，动不动就自己去做数据存储和管理是多么复杂啊！这样我们就不难理解为什么线性代数要定义叉积这样奇怪的运算了，它和C++把很多常用的算法和容器 纳入STL是同一道理。同样的，甚至你还可以在线性代数中定义自己想要的运算拿来复用。所以，数学一点儿不死板，它和程序一样是活活泼泼的，你理解了它的 来龙去脉就能驾驭自如。说到这里，我们就顺便回答一个很常见的疑惑：

线性代数的点积、叉积还有矩阵运算都很奇怪，为什么要定义这些运算呢？它们的定义又为什么是这个样子呢？

其实，和程序复用一样，线性代数定义点积、叉积和矩阵运算是因为它们的应用非常广，有很大的复用价值，可以作为我们分析和解决问题的基础。比如，很多问题都涉及到一个向量到另一个向量的投影或是求两个向量的夹角，那么就会考虑专门定义点积(Dot Product)这个运算：

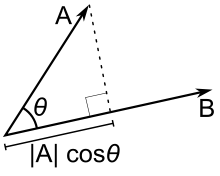
点积概念的提出属于设计，有发挥创造的余地；一旦设计定了，具体公式就不能随意发挥了，必须符合逻辑，保证它映射到初等数学模型的正确性。这就像一门高级语言可以定义很多概念，什么高阶函数、闭包等等，但是它必须保证映射到底层实现时在执行产生的效果符合其定义的规范。

上面说了，线性代数是一种高层次抽象模型，我们可以采用学习一门程序语言的方法去学习它的语法和语义，但是这一认识不只针对线性代数，它是对每一门数学学科通用的，可能有人会有疑问

微积分、概率论也是高层次抽象，那么线性代数这种高层次抽象的特点在哪里呢？

这就问到了根本上，线性代数的核心：向量模型。我们在初等数学中学习的坐标系属于笛卡尔所提出的解析模型，这个 模型很有用，但同时也有很大的缺点。坐标系是人为加上的虚拟参考系，但是我们要解决的问题，比如求面积，图形旋转、拉伸等应用都是和坐标系无关的，建立一 个虚拟的坐标系往往无助于解决问题，刚才三角形面积的例子就是这样。

向量模型很好地克服了解析模型的缺点，如果说解析模型代表了某种“绝对性”的世界观，那么向量模型就代表了某种“相对性”的世界观，我推荐把向量模型和解析模型看作对立的两种模型。

向量模型中定义了向量和标量的概念。向量具有大小和方向，满足线性组合法则；标量是只有大小没有方向的量（注：标量的另一种更深刻的定义是在坐标变换中保持不变的量）。向量模型的优点之一是其坐标系无关性， 也就是相对性，它在定义向量和运算规则的时候从一开始就抛开了坐标系的束缚，不管你坐标轴怎么旋转，我都能适应，向量的线性组合、内积、叉积、线性变换等 等运算全部都是坐标系无关的。注意，所谓坐标系无关性不是说就没有坐标系了，还是有的，刚才三角形例子的顶点就是用坐标表示的，只是在解决问题的时候不同 的坐标系不会构成影响。用一个比喻，Java号称平台无关，不是说Java就是空中楼阁，而是说你用Java编程时底层是Linux还是Windows往 往对你没有影响。

向量模型有什么好处呢？除了刚才三角形面积问题是一个例子，下面我再举一个几何的例子：

给定三维坐标系中的一点(x0, y0, z0)和一个平面a*x + b*y + c*z + d = 0，求点到平面的垂直距离？

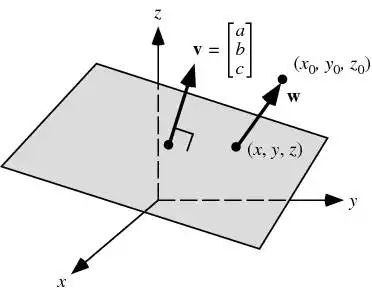
这个问题如果是要从解析几何的角度去解决几乎复杂到没法下手，除非是平面恰好是过坐标轴的特殊情况，但是如果从向量模型考虑就很简单：根据平面方程，平面的法向量(Normal Vector)是v=(a, b, c)，设从平面上任意一点(x, y, z)到(x0, y0, z0)的向量为w，那么通过内积dot_product(w, v)算出w到v的投影向量p，其大小就是(x0, y0, z0)到平面a*x + b*y + c*z + d = 0的垂直距离。这里用到了向量模型的基本概念：法向量，投影向量，内积，整个问题解决过程简洁明快。

下面再给大家留一道相似的练习题（熟悉机器学习的朋友可能会发现这是线性代数在线性分类中的应用）：

给定n维空间中的两点(a1, a2, ... an)，(b1, b2, ... bn)和一个超平面c1*x1 + c2*x2 ... + cn*xn + d = 0，请判断两点在超平面的同侧或异侧？

离开向量，下面我们要请出线性代数的另一个主角：矩阵(Matrix)。

线性代数定义了矩阵和向量、矩阵和矩阵的乘法，运算规则很复杂，用来做什么也不清楚，很多初学者都不能很好地理解，可以说矩阵是学好线性代数的拦路 虎。遇到复杂的东西，往往需要先避免一头陷入细节，先从整体上把握它。其实，从程序的角度看，无论形式多么奇怪，它无非是一种语法，语法必然对应了语义， 所以理解矩阵的重点在于理解其语义。矩阵的语义不止一种，在不同的环境中有不同的语义，在同一环境中也可以有不同的解读，最常见的包括：1)表示一个线性 变换；2)表示列向量或行向量的集合；3)表示子矩阵的集合。

矩阵作为一个整体对应的是线性变换语义：用矩阵A乘以一个向量v得到w，矩阵A就代表了v到w的线性变换。比如，如果想要把向量v0按逆时针方向旋转60度得到v'，只需要用旋转变换矩阵（Rotation Matrix)去乘v0就可以了。

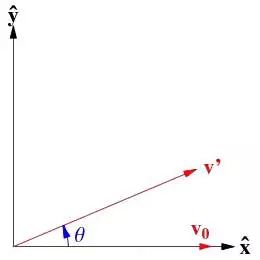
除了旋转变换，拉伸变换也是一种常见的变换，比如，我们可以通过一个拉伸矩阵把向量沿x轴拉伸2倍（请试着自己给出拉伸矩阵的形式）。更重要的是，矩阵乘法有一个很好的性质：满足结合率。这就意味着可以对线性变换进行叠加，比如，我们可以把“沿逆时针旋转60度”的矩阵M和“沿x轴拉伸2倍”的矩阵N相乘，得到一个新矩阵T来代表“沿逆时针旋转60度并沿x轴拉伸2倍”。这是不是很像我们Shell中把多个命令通过管道进行叠加呢？

上面重点介绍了向量模型的坐标系无关性，除此之外，向量模型的另一优点是：线性性，因而它能用来表示线性关系，下面我们来看一个熟悉的Fibonacci数列的例子：

Fibonacci数列定义为：f(n) = f(n-1) + f(n-2), f(0) = 0, f(1) = 1；问题：输入n，请给出求f(n)的时间复杂度不超过O(logn)的算法。

首先，我们构造两个向量v1 = (f(n+1), f(n))和v2 = (f(n+2), f(n+1))，根据Fibonacci数列性质，我们可以得到从v1到v2的递推变换矩阵：

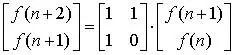
并进一步得到：

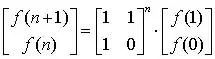
这样就把线性递推问题转化为了矩阵的n次幂经典问题，在O（log n）时间复杂度内解决。除了线性递推数列，初等数学中著名的n元一次方程组问题也可以转化为矩阵和向量乘法形式更容易地解决。这个例子是想说明，凡是满足 线性关系的系统都是向量模型的用武之地，我们往往可以把它转化为线性代数得到简洁高效的解决方案。

总之，我的体会是向量模型是整个线性代数的核心，向量的概念、性质、关系、变换是掌握和运用线性代数的重点。

本文提出了一种观点：从应用的角度，我们可以把线性代数视为一门特定领域的程序语言。线性代数在初等数学基础上建立了向量模型，定义了一套语法和语义，符合程序语言的语言契约。向量模型具有坐标系无关性和线性性，它是整个线性代数的核心，是解决线性空间问题的最佳模型。