图 1 奥卡姆剃刀定率

遵循“奥卡姆剃刀”简单就是最好的原则，归纳总结出各种雷达体制的差异主要体现在信号处理上。雷达从最初的大功率连续波收发分置雷达到目前广泛应用的各种新体制雷达，其中一个显著的区别在于原来的非相参雷达系统变为相参雷达系统。“相参”是指雷达发射或者接收的雷达脉冲信号的相位保持固定的关系，也就是已知的；“非相参”是指雷达发射脉冲信号的相位关系随机。因此从相参的基本概念出发，运用奥卡姆剃刀定律，利用相位信息来分析各种体制雷达系统信号处理上的内在联系。相参的本质就是“矢量相加，同相最大”，也就是“1+1=2”。“1+1=2“在这里表示的是矢量的叠加特性，直观上就是波的干涉。比如著名的双缝干涉实验，就是波的矢量叠加的典型例子。下面分别解释相位信息与相干积累、脉冲压缩、脉冲多普勒效应、相控阵雷达和合成孔径雷达等概念的基本关系，阐释“1+1=2”的内涵。

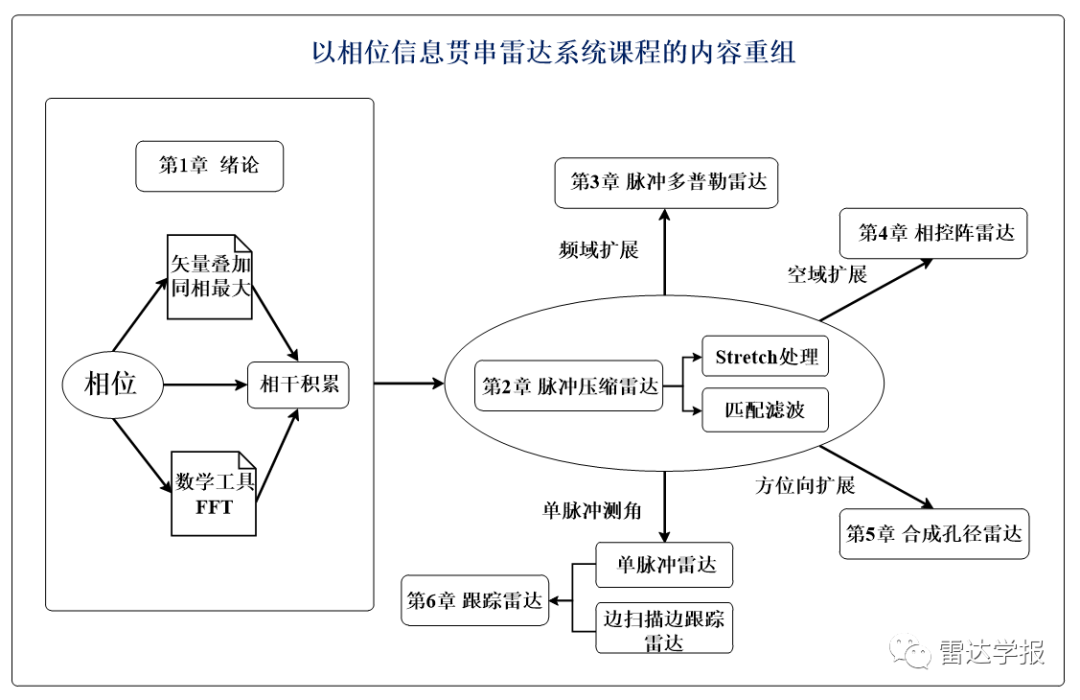
图2 雷达系统主体内容与相位的关系

相干积累是脉冲相位“相参”情况下的同相相加的处理结果。参与积累的脉冲个数就是信噪比提升的倍数。信噪比提升的主要原因就是信号在相位上是一致的，同相叠加使得功率变为所积累脉冲数目的平方倍数，而噪声功率变为脉冲积累数目的倍数，这就使得最终信噪比提高的倍数为相干积累脉冲的个数。

图3 相位与相干积累的关系

目前，脉冲压缩主要通过匹配滤波器实现。匹配滤波器在时域上就是信号的相关，等同于信号与系统中卷积的概念，是相参雷达系统的最大特点。在频域上很容易看到它与相位之间的关系：匹配滤波器的频域形式主要由两部分组成，即幅频特性和相频特性，幅频特性用来压制噪声，相频特性使得各频率成分相位完全相同，最终实现同相相加，与矢量同相相加的思想是一致的，因此脉冲压缩可以看作是脉冲内的相干积累。

图4 相位与脉冲压缩的关系

图5 相位与脉冲多普勒的关系

相控阵雷达的核心技术是通过移相器附加的相位，补偿空间路程差引起的相位差，形成空间信号的同相叠加从而实现波束最大指向。如果将各阵元接收的信号看成时域回波脉冲串，其空间指向可以等效为多普勒频率的变化，这样其波束方向也可以通过傅里叶变换处理得到，所以其本质还是相位的同相叠加。这一点可以引申到空时自适应信号处理、多输入多输出(MIMO)等新体制雷达系统。

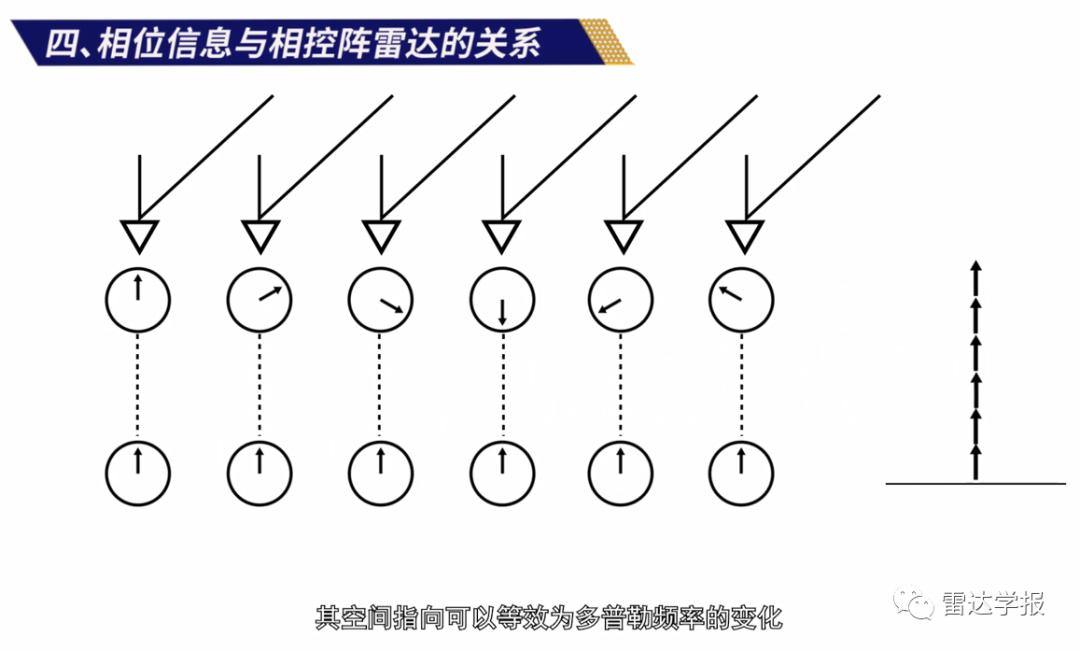
图6 相位与相控阵雷达的关系

合成孔径雷达本质上是二维信号的脉冲压缩。常采用距离-多普勒算法进行成像。首先经过距离向傅里叶变换(FT)进行距离像匹配滤波，然后进行距离徙动校正，最后通过方位向傅里叶变换实现方位匹配滤波，产生最终图像。可见合成孔径雷达是脉冲压缩的直接维数拓展，其本质还是相位信息的同相匹配。

图7 相位与合成孔径雷达的关系

综上所述，相位是一个可以贯串整个雷达知识的概念，因此雷达系统的主线可以确定为雷达信号的相位信息处理，这对雷达原理与系统的学习有很好的启发意义。