点击上方蓝字关注我们
周六锁定“温温故,知知新”,获取我司技术知识速递——您发挥才能,我们提供工具!别忘了参与文末有奖活动哦!
本篇文章是国际知名电源专家Christophe Basso所著的《开关转换器动态分析采用快速分析技术》的第一篇,完整文章共三篇,将陆续在我们的周六栏目上发布,欢迎大家持续关注~
开关转换器动态分析采用快速分析技术(一)
作者简介
Christophe Basso
安森美半导体法国图卢兹 Technical Fellow
他拥有超过20年的电子电路设计经验,在电力电子转换领域拥有近30项专利,他原创了许多集成电路芯片,其中代表性为NCP120X系列,它重新定义了电源低待机功耗设标准。
Christophe Basso出版了多部著作,《开关模式 SPICE 仿真和实用设计》深受广大工程师的欢迎并二次改版,《为线性和开关电源设计控制回路:教程指南》为工程师设计补偿和环路稳定性提供了实用指南,《线性电路传递函数:介绍快速分析技术》以说教的方式,为学生和需要强大的工具以快速分析日常工作中的复杂电子电路的工程师提供对电路分析的不同角度。
如果采用网格节点(mesh-node)分析能很好地求解电路的传递函数,那么立即获得一个有意义的符号公式通常是不可能的,需要额外的工作才能得出。应用经典的分析技术来获得所谓的低熵表达式–即分数形式,从中您可识别增益、极点和零点–往往导致如Middlebrook博士曾在他的文献[1]、[2]中提到的代数失效(algebraic paralysis)。
在此,快速分析电路技术(FACTs)可帮助您基于您在大学里学到的东西而扩展,以大大简化分析。通过使用FACTs,不仅加快您的执行速度,而且最终结果将以有序的多项式形式出现,通常无需进一步的因子分解工作[3]、[4]。
本文首先介绍后文用于确定开关转换器的控制到输出传递函数的FACTs。这个主题很大,在此我们只谈及表面,希望激励您进一步挖掘这个主题。我们选择了电压模式耦合电感单端初级电感转换器(SEPIC)工作于非连续导电模式(DCM)。PWM开关[5]将用于形成小信号模型。
01
快速分析技术(FACTs)简介
FACTs背后的基本原理在于电路时间常数的确定–t=RC或t=L/R–此时在两种不同的条件下观察所研究的电路:当激励信号降至0时和响应清零时。通过使用这种技术,您将体会到确定特定传递函数有多快和直观。基于这种方法的分析技术始于几十年前,如[6]和[7]中记载的。
传递函数是一种数学关系,它把激励信号、激励物,和由这种激励产生的响应信号联系起来。如果我们考虑一个线性时不变(LTI)系统无延时,具有静态增益H0–例如开关转换器的线性理想功率级-其连接控制信号Verr(激励)和输出Vout(响应)的传递函数H可表示为:
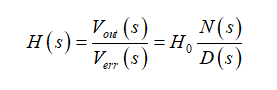
(1)
首项H0是系统在s=0评估表现出的增益或衰减。该项将带传递函数的单位(或维度),如果有的话。如果响应和激励都用伏特表示,在此我们表示为Verr和Vout,H是没有单位的。分子N(s)控制传递函数的零点。数学意义上,零点是函数幅值为零的根。通过FACTs,我们用数学抽象思维以轻松地揭开这些零点。我们不会像通常在谐波分析(s=jw)中所做的仅仅考虑在s平面的垂直轴,而是覆盖考虑到负数根的整个平面。
因此,如果电路存在零点,将表现为当输入信号调到零角频率sz时无信号的输出响应。在这种情况下,在变形的电路中的一些阻抗阻挡了信号传播,响应为零,尽管存在激励源:当变形的电路在s=sz点被激励时,在信号路径的串联阻抗趋于无穷或分支将该激励分流到地面。
请注意,这种方便的数学抽象通过观察提供了巨大的帮助来找到零点,通常无需写一行无源电路的代数。图1提供了简单的流程图,详细介绍了过程。关于这种方法的更多细节见[8]。
图一
点击查看大图 △
翻译参考▽
Bring the excitation signal – the stimulus – back in place:将该激励信号 – 激励-带回原处
Null the output:将输出清零
Identify in the transformed network, one or several impedances combinations that could block the stimulus propagation: a transformed open circuit or a transformed short circuit.:在变形的电路中找到一个或一些可阻挡激励传播的阻抗组合:一个变形的开路电路或变形的短路电路
Signal:信号
To response : 到响应
If inspection is not possible, go for a Null Double Injection(NDI):若观察无用,则进行双重抵消注入(NDI)
图1:这个简单的流程图将指导您用最简单的方法确定零点。在观察无用时,您将需要进行双重抵消注入或NDI。
分母D(s)由电路自然时间常数构成。通过设置激励信号为0和确定从电路中临时移除的所考虑的电容或电感“所示”的阻抗,来得出这些时间常数。
通过“观察”,您可想象把一个欧姆表置于暂时移除的储能元件(C或L),并读取它显示的电阻。这其实是个相当简单的运用,正如图2中的第二个流程图所详述的。

图二
点击查看大图 △
翻译参考▽
Count energy-storing elements with independent state variables:计算具有独立状态变量的储能元件
Assume there are two energy-storing element, L1 and C2:假设有两个储能元件,L1和C2
The denominator follow the form:分母遵循此公式
Open the capacitor, short the inductor, determine the dc gain H0 if it exists:电容开路,电感短路,确定直流增益H0,若H0存在
Reduce the excitation to 0 and determine time constants for b1 and b2:减小激励至零,并确定b1和b2的时间常数
Determine the resistance Ri driving LI while C2 is open circuited:确定驱动L1而C2 开路时的阻抗Ri
Determine the resistance Rj driving C2 while LI is short circuited:确定驱动C2 而L1短路时的阻抗Rj
Sum the time constants:将时间常数相加
Determine the resistance Rk driving LI while C2 is short circuited:确定驱动L1而C2 短路时的阻抗Rk
Determine the resistance Rl driving C2 while LI is open circuited:确定驱动C2 而L1开路时的阻抗Rl
Choose the simplest combination:选择最简单的组合
图2:该流程图解释了用于确定电路时间常数的方法。
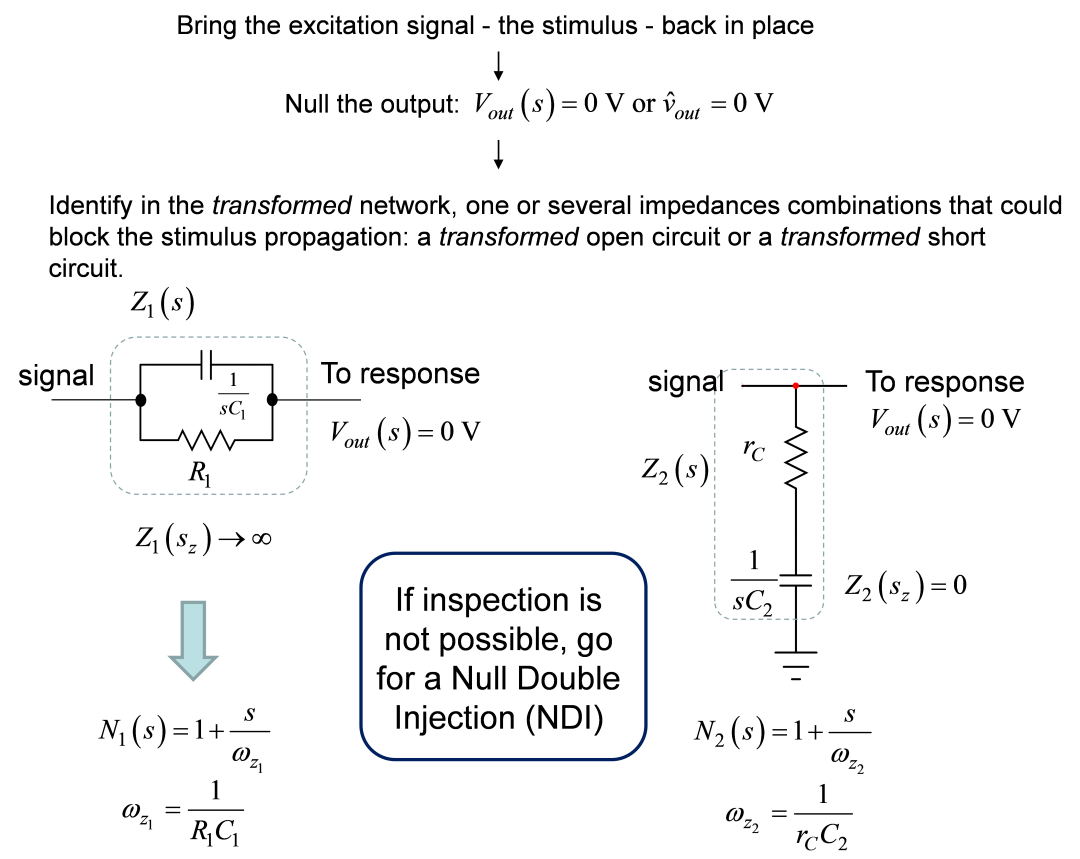
看到图3,是一个涉及注入源的一阶无源电路—该激励源—加偏压于左边网络。输入信号Vin通过网格和节点传播,形成您看到的电阻R3上的响应Vout。我们感兴趣的是导出连接Vout和Vin的传递函数G。
图三
点击查看大图 △
翻译参考▽
The response:响应
图3:确定电路的时间常数需要将激励源设为0,并看看从电路中暂时移除的能量存储元件所提供的电阻。
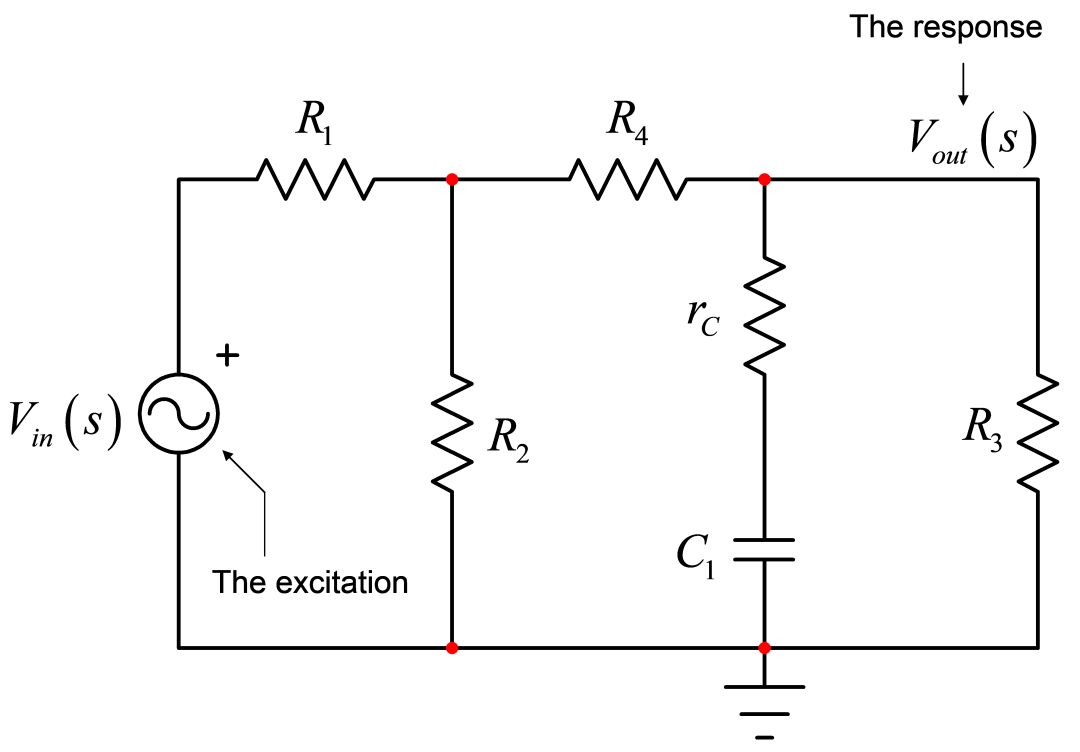
为确定本例电路的时间常数,我们将激励源设为0(由短路代替0V电压源,开路代替0A电流源),拆下电容器。然后,我们连接一个欧姆表来确定电容器端提供的电阻。图4指导您进行这些步骤。
图四
点击查看大图 △
翻译参考▽
The excitation is set to 0:激励源设为零
For example:例如
图4:由短路代替0V源后确定电容器端的电阻。
如果用图4的做法,您“看到” R1与R2并联后与R4串联,所有这些与R3并联后与rC串联。该电路的时间常数只通过R和C1即可计算得出:
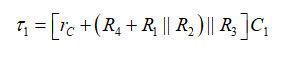
(2)
我们可证明第一阶系统的极点是其时间常数的倒数。因此:
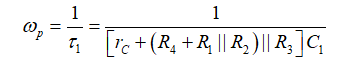
(3)
现在,s=0时该电路的准静态增益是多少?在直流条件下,电感器短路,电容器开路。把这概念应用于图3的电路,绘制成如图5所示。想象在R4前断开连接,会看到一个含R1和R2的电阻分压器。R2上的戴维宁(Thévenin)电压为:
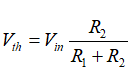
(4)
输出电阻Rth是R1与R2并联的值。因此完整的传递函数涉及到电阻分压器(由与Rth串联的R4和加载的R3所构成)。rC是断开的,由于电容C1在这直流分析中被移除。因此:
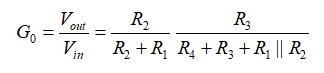
(5)
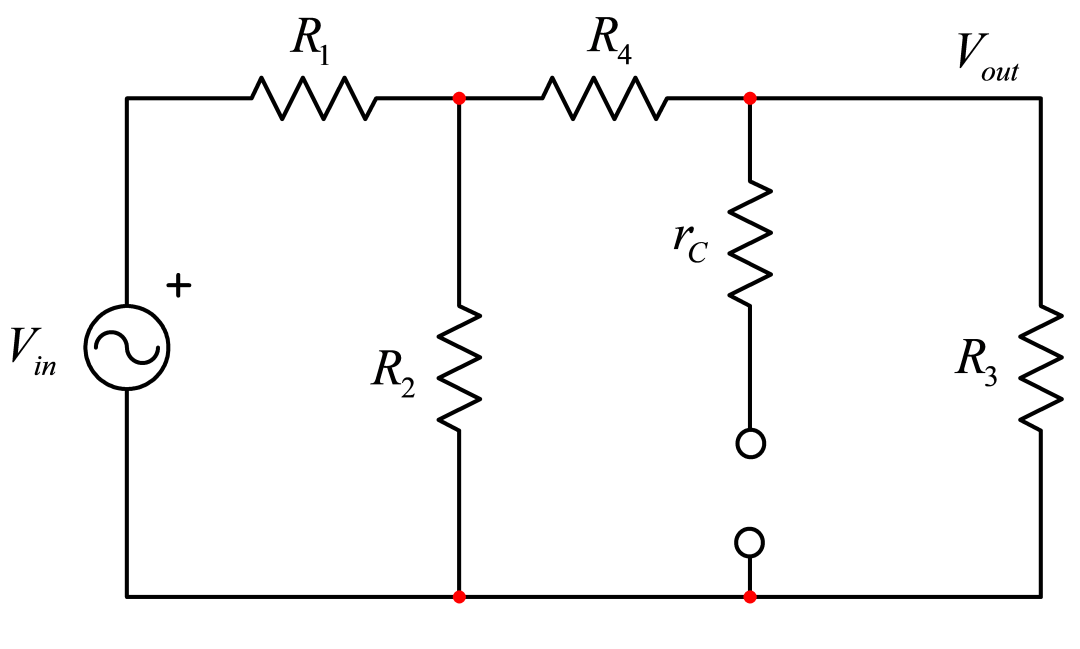
图五
图5:您断开直流电路中的电容器,计算这简单的电阻配置的传递函数。
基本就是这些了,我们正错过零点。我们在前文提到,零点通过阻断激励信号的传播而在电路中表现出来,产生一个无信号的输出响应(见图1)。
若我们考虑一个变形的电路–其中C1由代替–如图6,当激励源加偏压于电路,有什么特定的条件意味着无信号响应?无信号响应只意味流过R3的电流为0。这不是短路,而是相当于虚拟的接地。
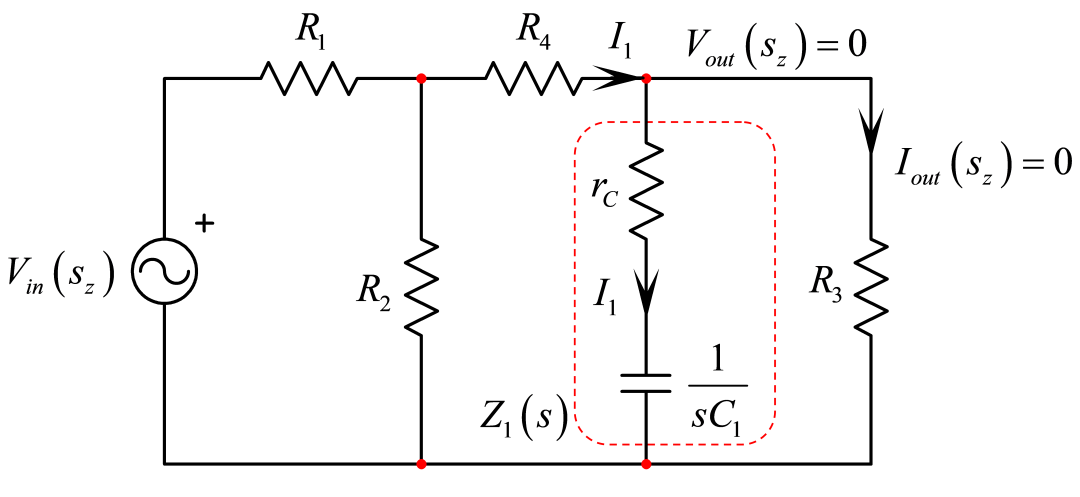
图六
图6:在这变形的电路中,当串联的rC和C1转化为变形的短路,响应消失,R3中无电流流过。
如果在R3中没有电流,那么串联的rC和转化为短路:
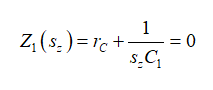
(6)
根sz是我们想要的零点位置:
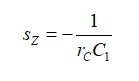
(7)
从而有:
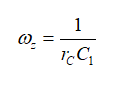
(8)
现在我们可组合所有这些结果,形成以图3电路为特征的最终的传递函数:
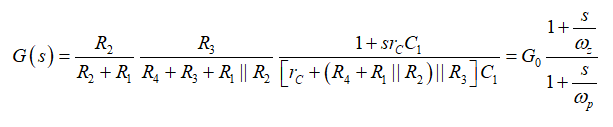
(9)
这就是所谓的低熵表达式,从中您可立即识别静态增益G0、极点wp和零点wz。高熵表达式将在考虑阻抗分压器时通过施加大规模外力到原来的电路来获得,如:
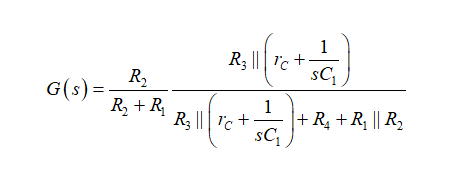
(10)
您不只在推导表达式时可能会出错—而且将结果格式化到像(9)这样需要更多的精力。另外,请注意,在这特定的例子中,在写(9)时我们没有写一行代数。如果我们后来发现一个错误,那么很容易回到一个单独的图纸并单独修复它。(9)的校正很简单。现尝试对(10)进行相同的修正,您可能会从头开始。
02
FACTs应用于二阶系统
FACTs同样适用于n阶无源或有源电路。通过计算状态变量是独立的储能元件的数量来确定电路的阶数。若我们考虑一个具有有限的静态增益H0的二阶系统,其传递函数可表示如下:
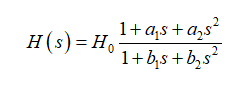
当H0带传递函数的单位,那么N:D的比值是没有单位的。这意味着a1和b1的单位是时间[s]。当a1无信号响应,b1的激励源为零,您将确定的时间常数相加。
对于二阶系数,a2或b2,维度是时间的平方[s²],你将时间常数结合为一个产物。然而,在这时间常数产物中,您重用了已经确定为a1或b1的一个时间常数,而二阶时间常数的确定需要一个不同的符号:
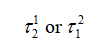
(12)
在这个定义中,您设置标号出现在“幂” 中的储能元件处于高频状态(电容被短路,电感被开路),当我们暂时从电路中移除二阶元件端(参见下标),您可从中确定电阻。当a2必须为无信号的输出和b2的激励源减为0时,您可运用此法。
当然,当观察有用时,它总是最快和最高效的得出N的方法。乍一看有点难以理解,但没有什么不可克服的,我们用几句话解释您就会明白。
图七
点击查看大图 △
翻译参考▽
Voltage-mode:电压模式
Small-signal mode:小信号模式
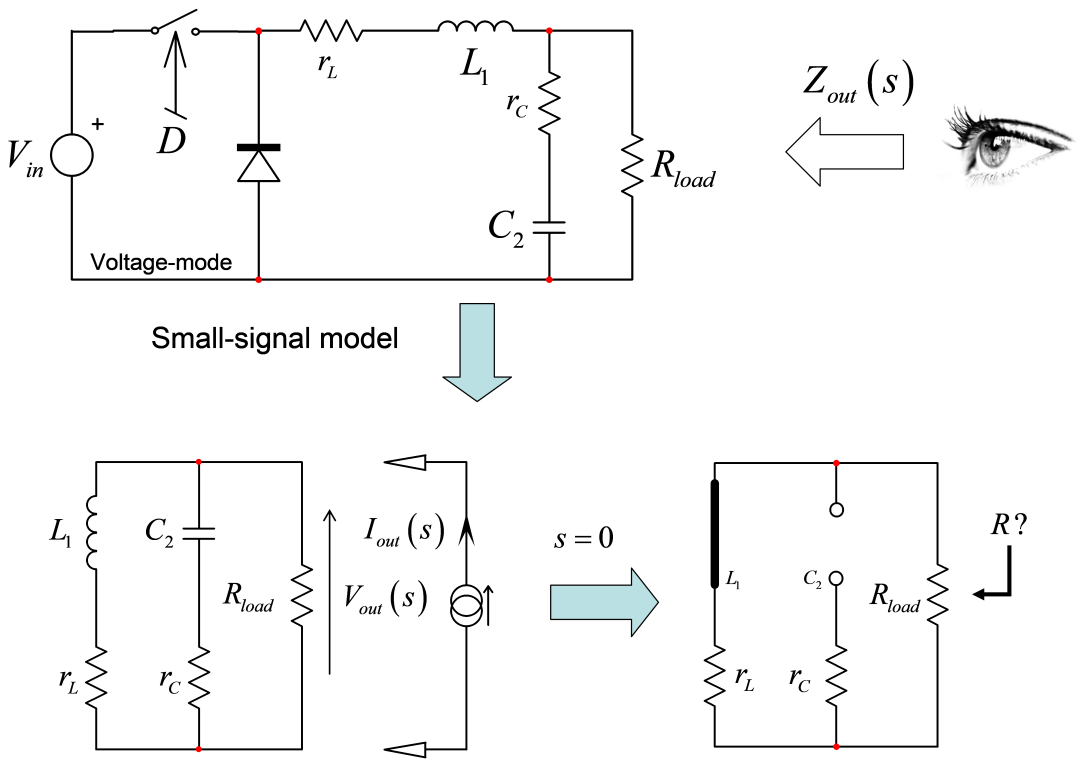
图7:工作于CCM的降压转换器的输出阻抗的确定是一个很好的例子,演示了FACTs如何简化分析。
图7是一个经典的二阶滤波器,用于确定在连续导通模式(CCM)中工作的电压模式降压转换器的输出阻抗。阻抗是连接一个激励信号Iout与响应信号Vout的一个传递函数。
此处,Iout是我们已安装的测试生成器,而Vout是其两端产生的电压。要从(11)中确定各种系数,我们可按照图2的流程图,从s = 0开始:如图所示,电感短路,电容开路。该电路是简单的,电流源的电阻R0不过是rL和Rload简单的并列组合:
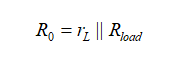
(13)
这个电路中有零点吗?我们看看图8所示的变形电路。我们看看当激励源电流Iout调为零角频率sz时,什么样的元件组合将使响应Vout为零。我们可发现两个变形的短路涉及rL–L1和rc–C2。
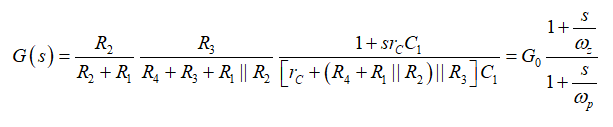
图八
图8:如果阻抗Z1或Z2转换为短路,响应Vout为无信号输出。
立即确定这两个阻抗的根:
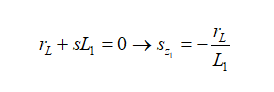
(14)
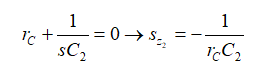
(15)
因此分母N(s)表示为
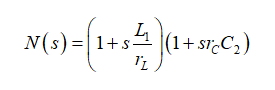
(16)
分母D(s)的一阶系数b1是由L1两端的阻抗提供,而C2处于直流状态(开路):有t1。然后看驱动C2而L1设置为直流状态(短路)时的阻抗:得出t2。如图9所示,从该草图可立即得出b1的定义:
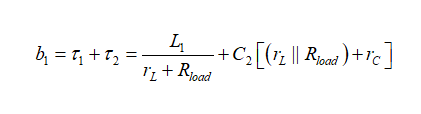
(17)
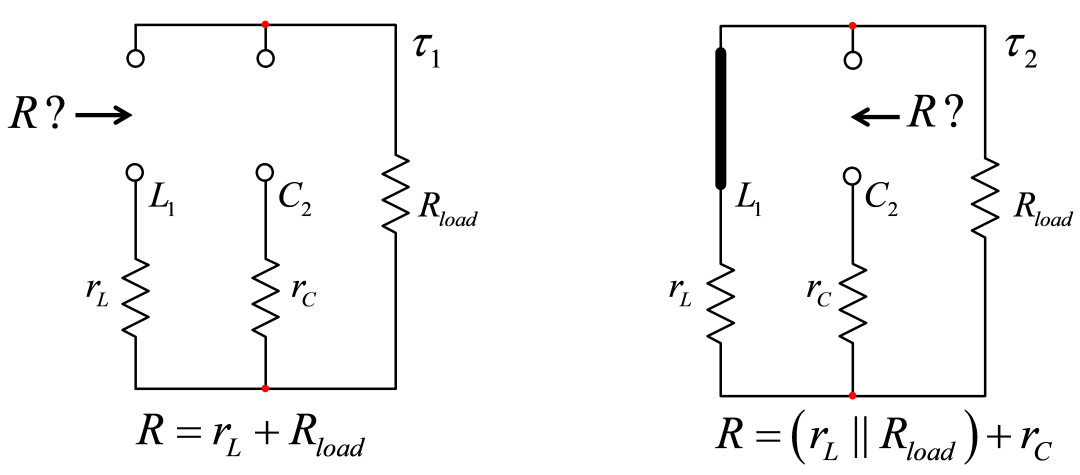
图九
图9:在选定的组件终端中,当第二个组件处于直流状态时,您会得出阻抗为多少?
二阶系数b2是用(12)中引入的符号来确定的。L1设置在其高频状态(开路),驱动C2以得到的阻抗,C2处于高频状态(短路),则驱动L1而得到的阻抗。图10显示了两种可能的整理结果。
您通常选择最简单的表达式,或避免不确定性的一个,如果有的话(如∞×0或∞/∞)。下面对于b2的两个定义是相同的,您看上面的是最简单的:
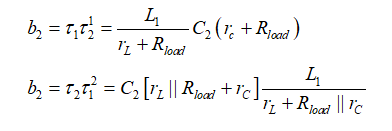
(18)
现在我们有所有的成分来组合最终的传递函数,定义为:
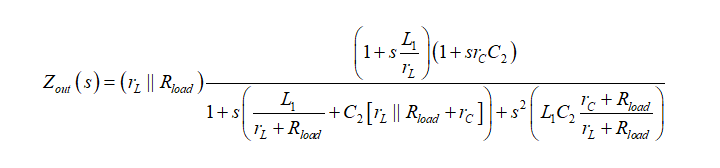
(19)
我们已经确定了这个传递函数,而没有写一行代数,只是拆分该电路为几个简单的草图个别解决。
此外,正如预期的那样,(19)已经是一个规范的表达式,您可轻易的看到一个静态增益、两个零点和一个可用一个谐振分量w0和一个品质因数Q进一步整理的二阶分母。如果不是迅速考虑Z1、Z2 和Rload的并联组合,我们不可能得到这一结果。
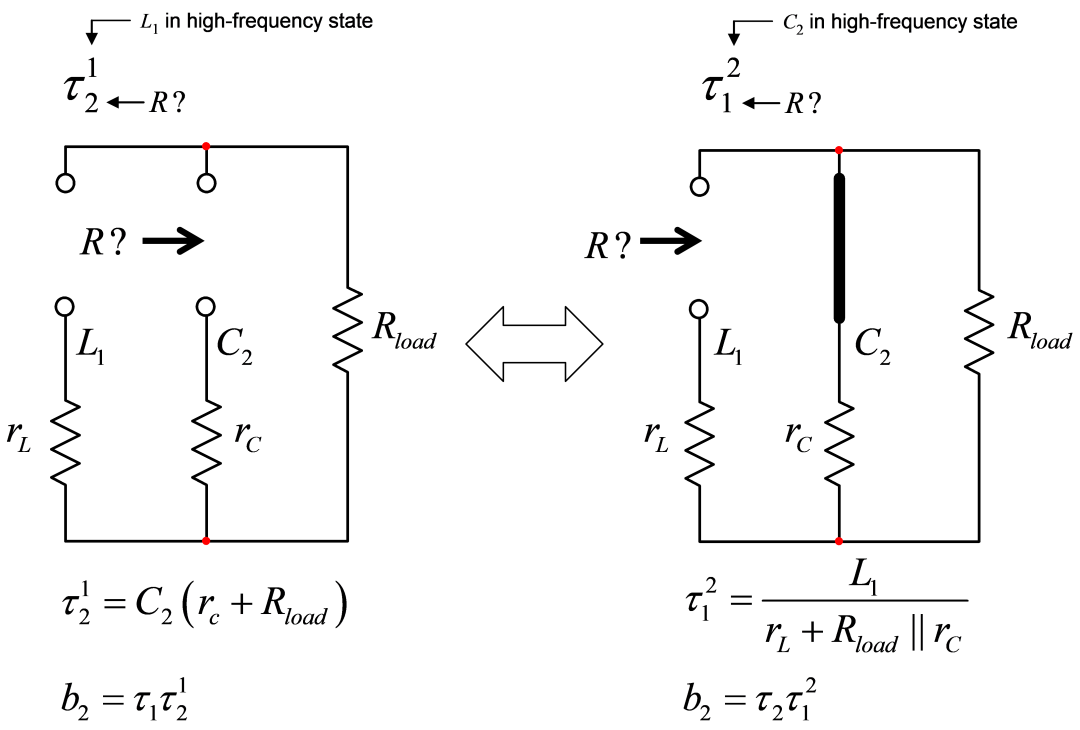
图十
图10:在选定的组件终端中,当第二个组件处于高频状态时,您会得出阻抗为多少?
采用FACTs,通过观察可导出传递函数,特别是对于无源电路。由于电路复杂,包括电压或电流控制源,观察起来没那么明显,您需要利用经典的网格和节点分析。但FACTs提供了几个优点:由于您将电路拆分为用于确定最终的多项式表达式系数的小的单个草图,因此如果在最终的表达式中发现一个错误,您总是可以回到一个特定的绘图并个别修正。
此外,当您确定与传递函数的ai和bi相关的项时,您自然会得到一个多项式表达式,而不用投入进一步的精力来收集和重新排列这些项。最后,如[4]所示,在复杂的无源和有源电路中,SPICE对验证个别极点和零点的计算有很大帮助。
未完待续,下周六见...

