干货！高速串行Serdes均衡之FFE

图1 

其中数字信号表示为{dk}，这里为方便叙述，dk取值归一化为±1，分别代表逻辑“1”和“0”。其转化关系为是线性的。同样将TX输出y(t)归一化为±1的波形如图2。可以将TX的单位冲激响应Φ(t)看做是一个窗函数rect，也就是一个零阶保持器（Zero-order Hold，ZOH）。Tx Driver就通过ZOH完成了离散信号到连续信号的转换。

如图2，经过ZOH连续化的NRZ编码信号，可以分解为1UI宽度的幅度为±1的脉冲信号了。

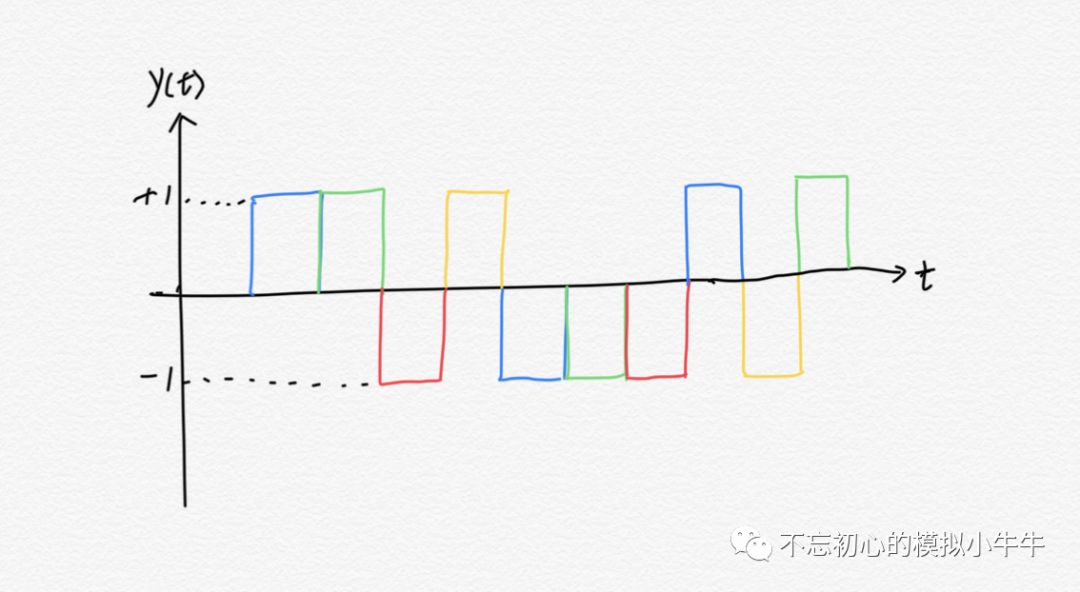
图2 

从信号与系统中，我们知道，满足采样定理的原始信号经过采样后，为了重建（reconstruction）原始信号，需要对采样信号在频域加理想窗函数rect。

如图3，rect和sinc函数是一对傅里叶变换对。频域窗函数rect其时域则是sinc函数。这种理想信号重建方式，实际上，比较难以实现。

ZOH作为最简单的离散信号连续化手段，其对应的频域是个sinc函数。可以看到，频域sinc函数衰减了高频成分，虽然无法完全消除。但因其时域的实现方式简单容易，而广泛应用。

图3 

在TX的信号转化模型中，我们可以看到，将离散非周期信号{dk}转化为连续非周期信号y(t)，采用的是ZOH的零阶保持。对应的频谱从连续周期变化为连续非周期。这是因为表示ZOH的矩形窗函数rect在频域是连续非周期的sinc函数。过程如图4，也就是频域经过sinc函数整形。

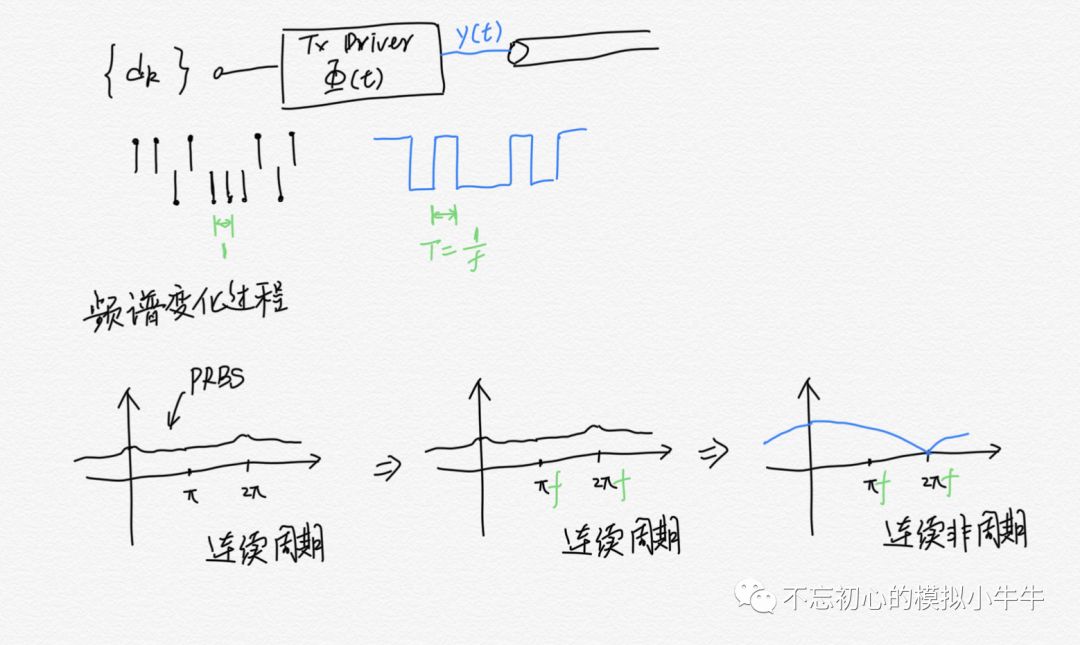
图4

总结一下，就是TX发送端完成了离散数字信号的连续化。

对于一定的信道，随着SerDes的数据速率越来越高，数据传输到接收端时，已经比较难以分辨了，接收端会得到大量的错误数据。至于信道模型，基本都是等效为我们先前聊过的传输线。图5给出几个不同长度FR4板材的传输线特性，主要是插入损耗S21随频率的变化曲线。

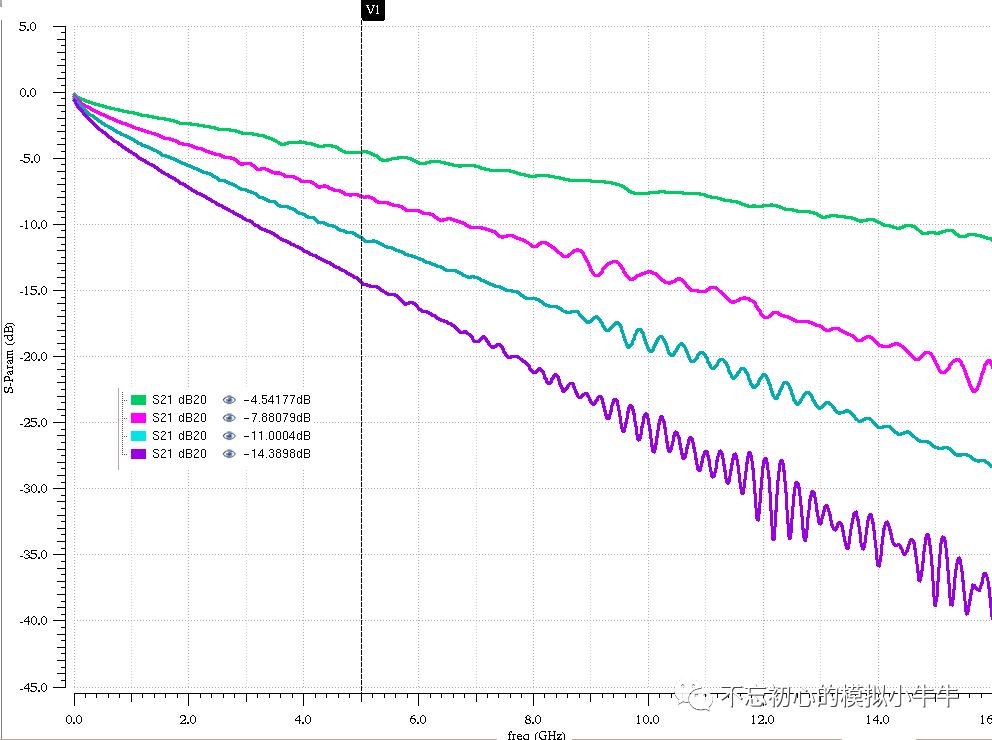
图5

可以看到在设计的比较好的信道时，其损耗和频率的关系相对比较线性。信道对不同频率成分的衰减量是不一致的。而实际信号的频率会比较丰富。这会导致信号有比较严重的码间干扰（后边具体说明）。

因此需要在接收端RX，采用不同的均衡手段，来降低信道的低通频率特性的影响，但为应对更大的信道衰减，在更高的数据率下，也需要在发送端集成均衡方案。这种均衡方式常称为前馈均衡（Feed-Forward Equalization，FFE）。利用的是数字信号处理中最常见的有限长度冲激响应（Finite Impulse Response）滤波器。

那么对于SerDes的发送端均衡，我们要考虑的FIR就必须具有高通特性，以此来提前补偿一定程度的信道损耗。

至于具体的FIR实现上，需要分析FIR的补偿量，阶数。同时综合考虑应用场景特性，发送端电路实现和用户的易用性等因素。图6给出了个简单的2阶3-tap结构的FIR例子。

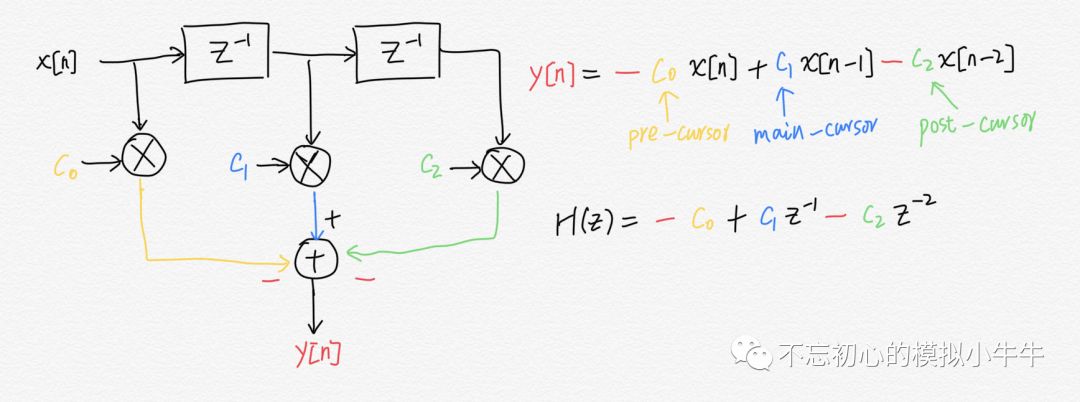
图6 

其中3个tap的系数就是设计参数，尽管我们已经确定需要FIR的频域特性是高通特性。但考虑到电路实现时（特别是功耗这一点上），就有两种不同的FIR的两均衡方式，分别称之为预加重（Pre-emphasis）和去加重(De-emphasis)。其归一化频域特性和离散时域表达式如图7所示。

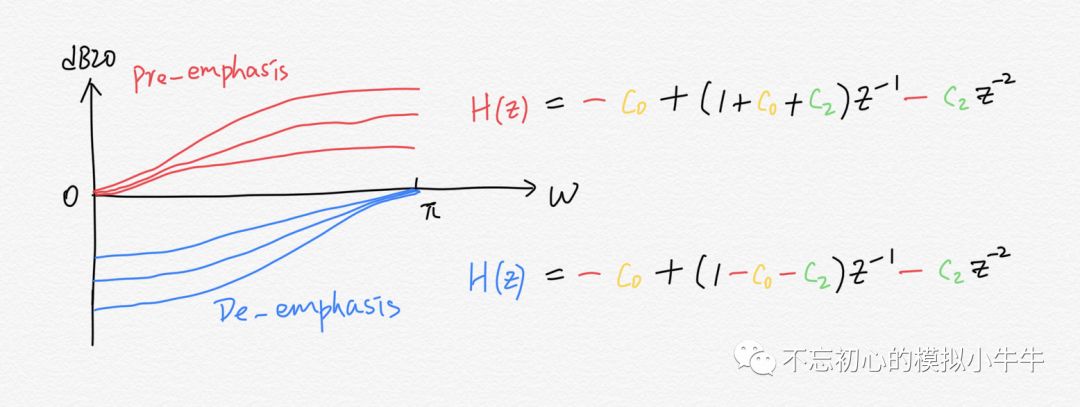
图7 

看到预加重和去加重的典型区别是，在多档可调均衡量设计中，是否具有恒定的最大输出摆幅（也就是fixed peak swing）。比如说去加重就是典型的fixed Vpk。而预加重的最大输出幅度和加重量相关。表现为图7中归一化奈奎斯特频率是否恒定。

加重量的计算可以直观从图7表达式看到。DC频率幅度和奈奎斯特频率幅度比值取对数坐标即可。

可以这么理解，去加重方式主要是降低中低频分量，保持高频分量恒定；而预加重主要是保持低频恒定，增加中高频分量。给定图7所示系数C0=0.1,C2=0.2，一个典型的去加重和预加重波形如图8所示。

图8

如果说发送端在无均衡模式下，只能看做1bit的D/A转化器，那么包含FFE均衡的发送端就是多bit的ADC了。在实际的实现过程中，无论是电压型的SST结构和电流型的CML结构。都可以采用了多份叠加的实际思路，如图9的示意图。

图9

那么现在还剩下一个问题就是FIR的系数怎么确定，为什么c0和c2要取负值。回答这个问题前，我们先了解下信道的脉冲响应。

如图10所示。10Gbps数据率下，对应图5不同损耗的单位脉冲响应。可以看到随着损耗的增加，响应信号最大幅度逐渐减小，并表现出了越来越严重（幅度和持续时间）的“拖尾”，这就是我们常说的码间干扰（ISI）。

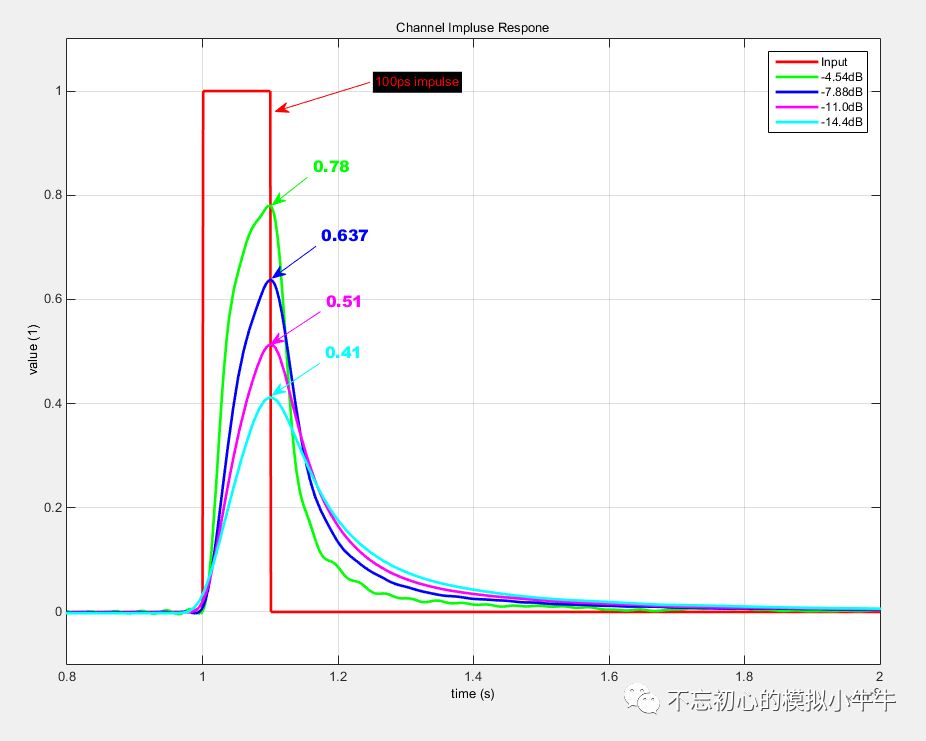
图10

可见在需要长距离传输时（通常损耗量和长度正相关），为保持信号尽可能的小的衰减，就需要使用更好材质的传输线，或更进一步使用光纤传输。

为了更形象的理解ISI的干扰作用，图11和图12给出了更进一步的说明。

图11是一个典型的信道输入信号的脉冲分解。这里脉冲初值给了0（对应实际的发送器输出为idle态，也就是共模）。之后是“1111101”的脉冲。将该输入送给图10中具有-14.4dB@5GHz的信道。

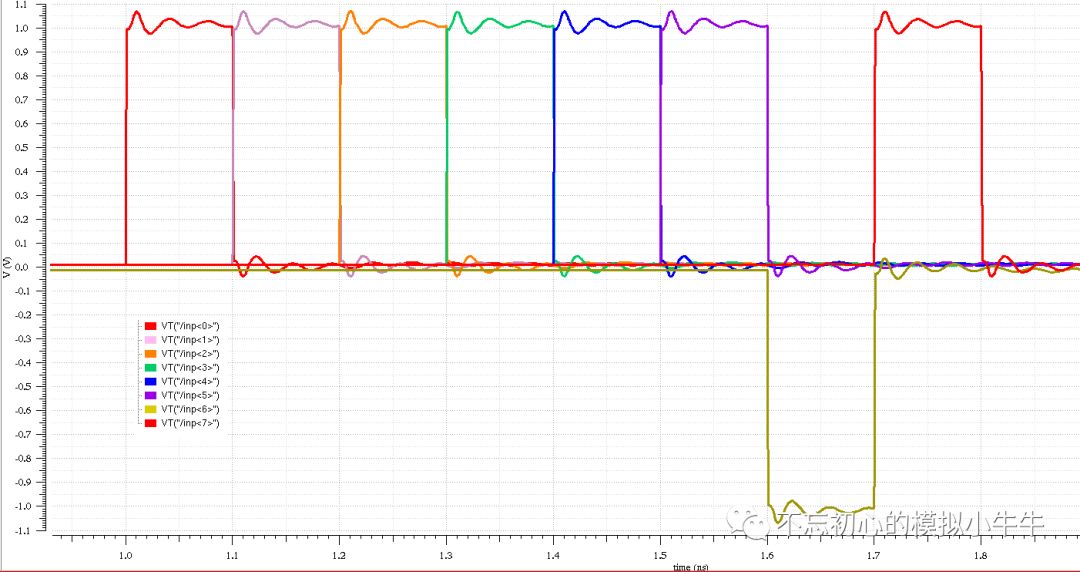
图11

图12是输出结果波形。信道通常是LTI系统，可以看到8个相隔为1UI=100ps的脉冲响应。还有一些叠加信号，黄色是仅前3个+脉冲的叠加结果，蓝色为前6个+脉冲的叠加，红色为前6个+脉冲加第7个-脉冲的叠加结果，黑色为全部8个脉冲的叠加结果。

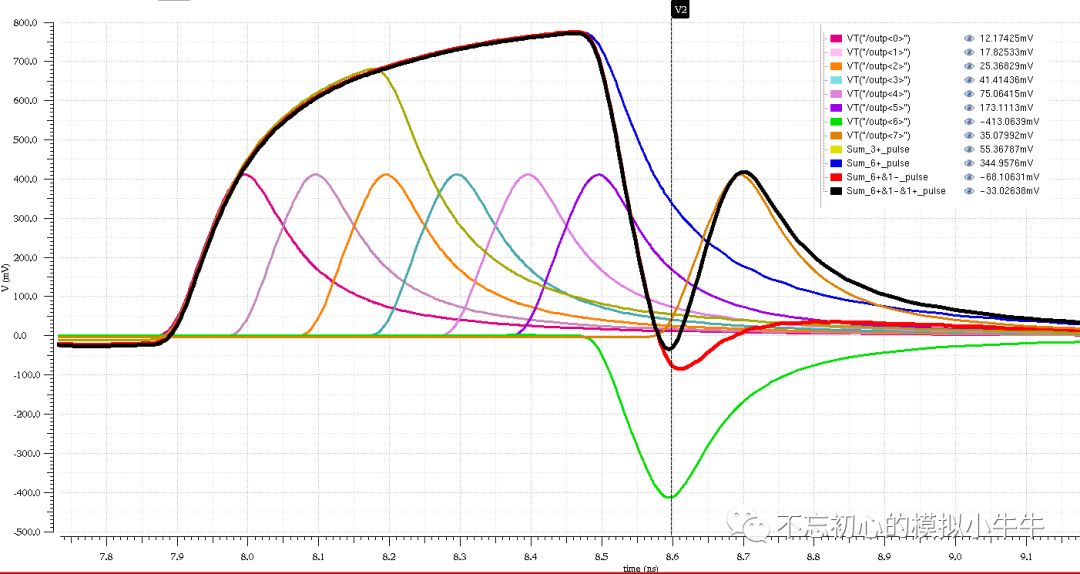
图12

从图12比较明显地观察到，前6个+脉冲和第8个+脉冲的影响，导致第7个-脉冲的幅度裕量（和0电压比较）很小了。如果再加上噪声和其他干扰，比较容易导致RX端判断错误。下边量化一下ISI的影响。

图13给出-14.4dB@5GHz信道的脉冲响应，包括前标（pre_cursor）、主标（main_cursor）和后标（post_cursor）的具体量值。这些标量在计算经过信道后眼图的“眼高”时有重要指导意义。

比如图13中给出了出现最小眼高的Case。一般是在出现连续多个UI的逻辑“0”(或“1”)之后，紧接着出现逻辑“10”(或“01”)，或者相反的情况（图12例子）。

图13

需要注意的worst case眼高值y的计算公式。当然实际上眼高和数据密切相关，比如我们在用PRBS7和PRBS15等进行仿真时，可以明显看到PRBS7的眼高就比PRBS15的更大一些。这里边就是因为PRBS7码型最多出现7个连续的逻辑“0”或者“1”。导致计算式中post_cursor的和偏小。worst case的“眼高”估计，是RX端设计的重要参考指标。

最后就是FIR系数计算方式，一种是迫零法（Zero Force），另一种是最小均方误差（Minimum Mean Square Error，MMSE）。

限于篇幅，这里给一个迫零法的简单说明。这里利用图13中给出的14.4dB的脉冲响应，计算一下实现图6和7中3-tap结构FIR。可以看到FIR系数的计算就是利用脉冲响应构成的矩阵运算，其中P是无前后标的理想脉冲响应[0 1 0]，归一化后可以得到系数的计算结果。

图14

MMSE不不强迫后标都是零值，而是使所有后标的总能量最小。是一种比迫零法更好的方法。

需要说明的是，在我们FIR的实现中，可以只用Pre-cursor C0(C2=0)或者Post_cursor C2(C0=0)进行均衡加重，也可以两者都用，区别表现在TX输出的幅度稳态值个数不同。

最后再放一张包含了同时包含Pre-cursor去加重和post-cursor去加重量的发送端眼图。可以在图15的眼图上看到约6个稳态幅度量。分别代表了高中低等频率分量。

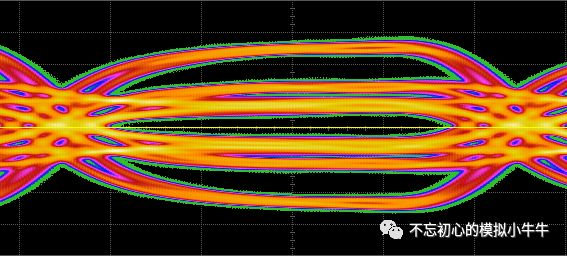
图15

到了最后还是不得不说一下TX端均衡的局限性，最主要的就是发送器的均衡程度很难做好根据应用场景的自适应调节。一般都是留一些可调整的档位供用户选择。但这不妨碍TX端的均衡能够进一步提高SerDes的过channel能力，提高串口的性能。总之，属于锦上添花的feature。