
中学物理学过,空间中的变化的磁场和电场会相互激发,即所谓磁生电,电生磁。
那么,这种变化的电磁场在空间中移动会产生什么后果呢?
很多人脱口而出——电磁波!
对的!但问题是,波不应该是某种振动在空间中的传播吗?
例如,声波就是机械振动在空气中的传播。它的振源是一个位置作周期变化的质点,它通过弹力带动周围的空气质元振动,这种振动的传播就形成了声波。
简言之,声波由振动的质点引起,描述质元的位移随时间和位置的变化。
类似的,你自然就会想到,电磁波由振动的电荷引起。
没错!那么振动的电荷引起什么在空间中传播呢?
既然电磁波可在真空中传播,真空中没有电荷,振源电荷带动的不可能是电荷吧?所以电磁波描述的不可能是电荷的位移,更不可能是电荷本身。
那是什么呢?只可能是电场和磁场!
是的,电荷激发电场,运动的电荷还激发磁场,它们就像围绕着电荷的两团云雾一样。电荷振动,这两团云雾自然就会跟着抖动起来,这一抖动,就像湖水被搅动一样,波浪就会向外传播。
你可能会有一个疑问:既然静止的电荷周围有电场,那它由近及远的传播算不算电磁波呢?
这个问题本身是矛盾的,既然你说静止电荷,那么它在那里不动已经很久了,它的电场早就传到了足够远的地方,然后维持不变了。它的电场就像平静的湖水一样,是静态的,所以没有电磁波。

你又想起:匀速运动的电荷的电场应该是不断变化的吧!这一变,就会导致由近及远的扰动,会导致电磁波吗?
答案是:不会!
解释这个答案之前,先摆两个很浅显的事实。
一根长长的弹簧,一端固定,现在你匀速地拉或压它的另一端,你看到弹簧上会有波产生吗?当然不会,除非你用力反复拉和压,这时候纵波产生了。

一根绳子,一端固定在墙上,你手握另一端让其处于水平位置。若你匀速向上或向下,我敢肯定,不会有波沿着绳子传播,除非你上下抖动绳子,这时候横波产生了。
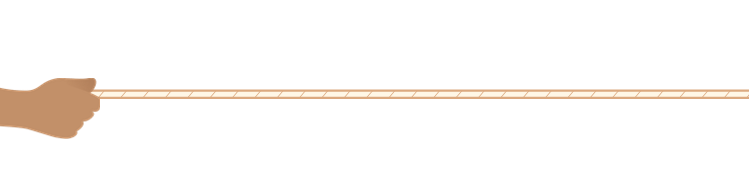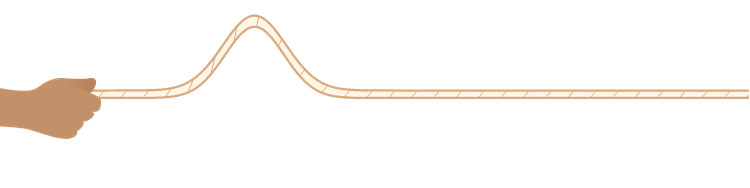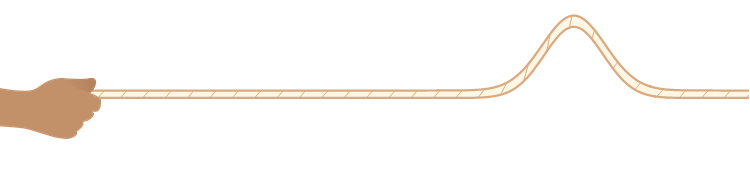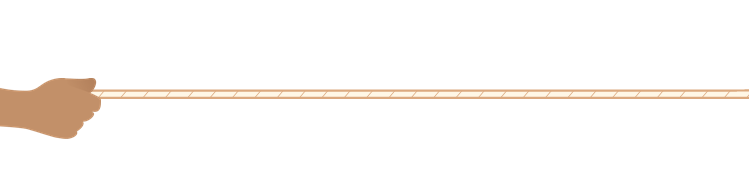
所以,要产生波,必须使相应的物理量在某个方向上有分量,而且是来回往复地变化量。对纵波来说,这个变化量沿着波的传播方向;对横波来说,这个变化量沿着垂直于波的方向。
什么是波的方向?就是从振源指向波所传到的地点的方向。对振动的电荷来说,它就是从电荷指向四面八方的任意一个方向。若以电荷为原点,那么任意径向就是波线方向,与之垂直即为横向。
不知道什么叫径向和横向?只要是从原点出发的直线就代表径向,曲线就是非径向。与径向垂直的就是横向。
所以,电荷要激发电磁波,必须具有横向的电场分量。
好了,现在可以回答上面的问题了:为什么匀速运动的电荷不能发出电磁波?
因为电磁波是横波,要产生电磁波,必须有横向的电场分量。但计算表明,匀速运动的电荷只有径向的电场分量!
当然,对此回答,你大概有两点疑惑:
第一,为什么电磁波是横波?
第二,为什么匀速运动的电荷的电场只有径向分量?
第一点暂时先放一下,后面再来证明。
至于第二点,思路倒是不难。
想想这样一件事:一个人从你身边径直远离你而去,你看着他,他的轨迹当然是直线。但若你在原地转动,你会感觉他的轨迹变成螺线了。这两个轨迹之间如何相互变换?
答案是:坐标变换。
类似的,物理问题可在不同的参考系中描述,从一个参考系变到另一个参考系,也是用坐标变换。坐标变换有两种,低速运动时用伽利略变换,高速时用洛伦兹变换。
在电磁学里,无论速度多少,伽利略变换都不适用,必须用洛伦兹变换。
设某坐标系K'相对于K系沿它们公共的x轴正向运动,相对速度为
其中
设K系原点处有一静止的电荷
怎么样?这个结论乍一看觉得有点违反直觉吧!那只怪你的直觉是错的,匀速运动电荷和静止电荷的电场确实是沿着径向的。
到此,问题的第二点讲完了。
再来关注下匀速运动的电荷的电场和磁场的特点。
下面是一个静止电荷和一个水平匀速运动的电荷的电场的样子。
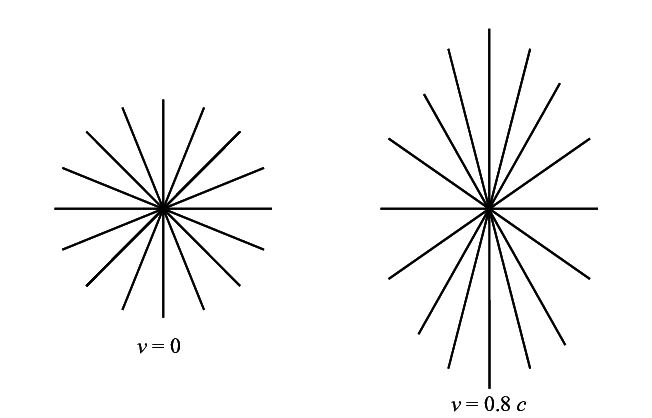
从上图可见,对匀速运动的电荷来说,电场始终沿着电荷的径向,说明电场的分布与电荷同步移动。对高速电荷,电场更集中于横向的面内。
至于磁场,根据前面的公式(低速时就是毕-萨定律)可知,它的场线是一系列与速度方向垂直的环。磁场沿电荷速度方向的分量始终为零,这说明它的分布也是与电荷同步移动。对高速电荷,磁场的环也更集中于横向的面内。
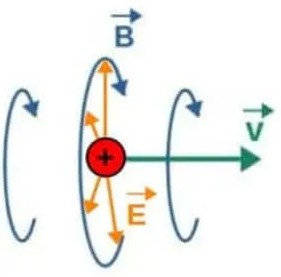
所以,匀速运动的电荷的电场和磁场就像被电荷带着一起飞似的,它们的分布完全与电荷的运动同步,并无任何波动的特点。
讲到这里,你可能会问有点疑惑:按你这讲的,稳恒电流的电场和磁场的分布是不是在移动,既然那电荷都在运动?
稳恒电流中,虽然载流子在非常缓慢的移动,但总体来讲,电荷的分布不变,所以电场分布的移动可以忽略。
注意一个细节,这里没说电场或磁场随着电荷移动,只说它们的分布随着电荷移动。
总之,匀速运动的电荷无法产生电场的横向分量,所以没有电磁波发出。要发出电磁波,只能靠加速运动的电荷了。因为加速的电荷的电场线会拐弯,如下图所示。这样的电场线才具有横向分量,满足电磁波产生的条件。
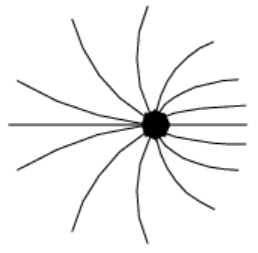
那么就来看看,加速电荷究竟是如何产生横向电场分量的?
设有静止于O点的电荷
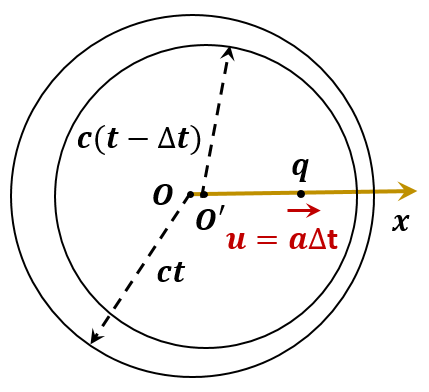
考察匀速运动的某时刻
一方面,从0时刻发出的电场线已抵达半径为
由于加速时间
既然电荷加速所引起的影响最远只到球面1,故球面1之外的电场还是电荷原来静止时激发的电场的样子——沿O点的径向往外。
而加速结束后发出的电场最远只到球面2,又根据前面所讲,匀速运动电荷电场分布总是随着电荷一起移动的,故球面2以内的电场总是沿电荷的径向。
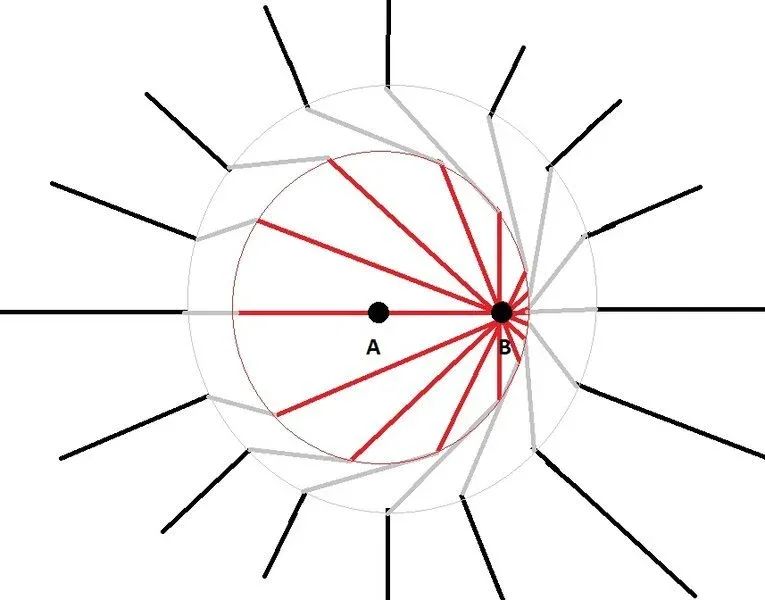
根据高斯定理,包围该电荷的任意闭合曲面穿过的电场线的条数相同,因此在球面1和2之间的过渡区的电场线是连续的。
这说明,球面1内的电场线必然与球面2外的电场线成对的连起来。但它们的方向又不同,所以在过渡区,电场线必然发生扭折,这就导致横向电场分量了!
随着电荷的运动,过渡区的半径越来越大,如下图所示。随着横向电场扩散到更远的地方,电磁波也随之传到那里了。

以上分析中,为了使问题简单,假设电荷只加速一小段时间,所以存在一个过渡区。导致电场线折扭。实际上,如果是振动的电荷,它始终在加速,它的电场线有无数个连续的过渡区,最终形成光滑的弯曲电场线。
例如当电荷绕着圆圈高速旋转时,会导致它的电场像下面这个样子。是不是隐隐的感觉到一种由近及远的波动效果?

不过,这个横向的电场到底有多大呢?
经过一个简单的计算(此处略)可知,离电荷
横向电场分量随着距离反比例的衰减,但你看到没有,径向分量按距离的平方反比衰减,所以横向分量比径向分量衰减慢!这使得在足够远的地方,横向电场贡献了电磁波的主要成分。
说完了加速电荷的电场,再看它的磁场。
既然电场知道了,磁场就按照安培环路定理来计算了,由电荷加速运动导致的磁场沿着与横向电场成右手螺旋关系,沿着方位角的方向,经过计算(此处略)得其值为
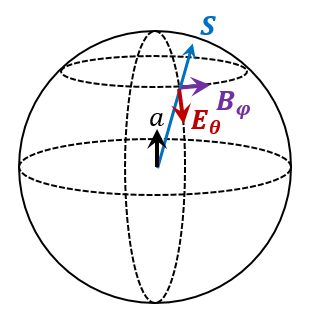
波既然总是沿径向传的,那么横向电场和横向磁场都垂直于波线,因此电磁波必然是横波!电磁波本身就是横向场分量的振动在空间中的传播。
还有一个值得注意的事情是,无论电场还是磁场,它们的横向分量都包含因子
你可能有点不耐烦了:扯半天,到现在还不见电磁波的影子啊!

不急不急,马上就来!
既然电磁波只需要考察横向场分量,现在把这俩分量写一起再看看,不再带下标了——反正离电荷较远处,只剩下它俩了。
想一想,在简谐振动
这个简单,加速度是位置的二阶导数,即
所以,当一个电荷作简谐振动时,它的加速度也在作简谐振动嘛!
根据电场和磁场的表达式,既然它们都在分子上含有一个
没错!写出来就是
再考虑这种振动在空间中传播,抵达
在振动方程基础上考虑相位滞后,得波函数为
电磁波是横波,电场和磁场同频同相振动,其效果图如下。
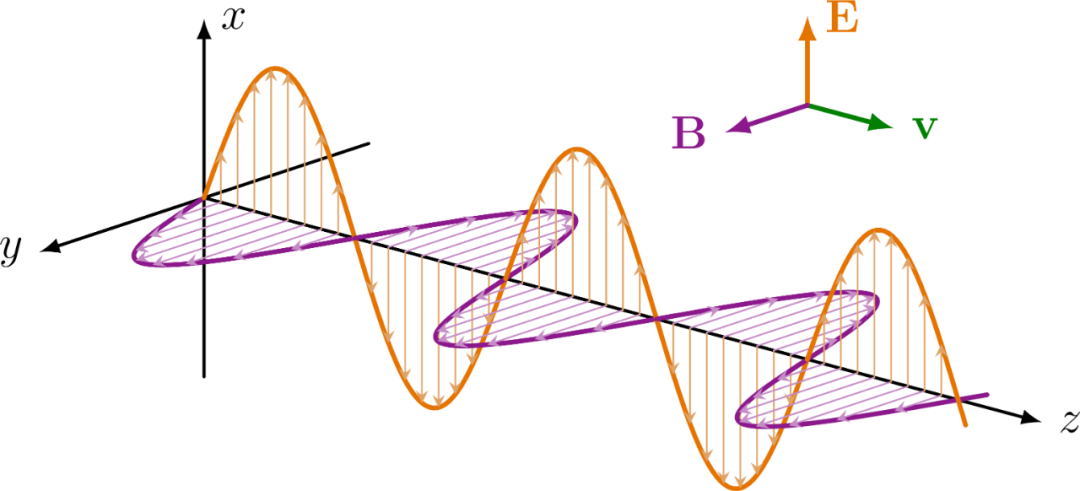
再来个动图领会一下。
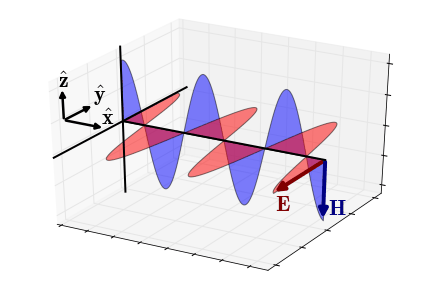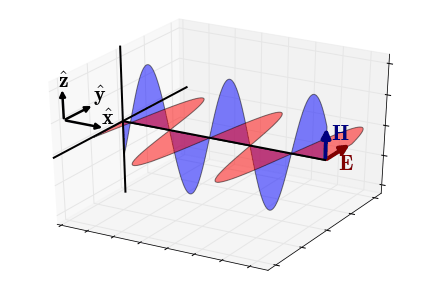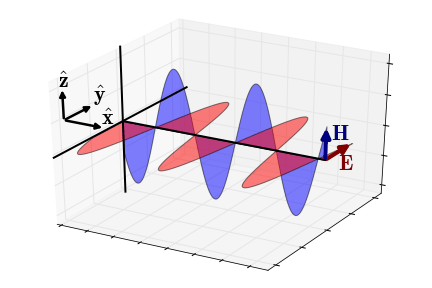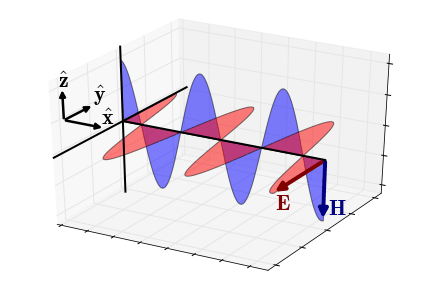
好了,咱已经成功的从加速电荷推导出电磁波了。
接下来的一个问题是,实际要发射电磁波,用什么方法让电荷一直听话地在那里简谐振动呢?
一个电荷的确不好操作,但成对的电荷就好搞了,阴阳搭配,干活不累嘛。一对等量异号电荷一分一合,不断循环,这就相当于每个电荷都在作简谐振动了!
用什么方法能达到这个效果?
它就是中学物理中学过的LC振荡电路,如下图所示
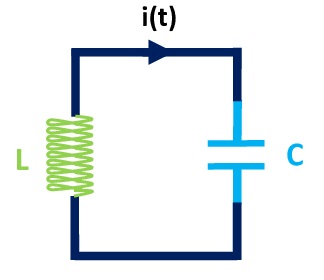
它的两个极板上带有等量异号电荷。由电路的知识可知,电荷量
不过,要想将电磁波传出去,上面地电路需要作两方面地改造。
一方面,电路振荡地频率要足够高,才能提供足够的能量将电磁波辐射到更远的地方。所以要极可能的减小
另一方面,电路应更加开放,这样才能更好的将电场合磁场分布到空间中去。
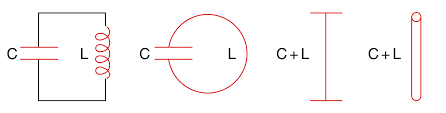
据此原则改造后,LC电路变成了天线,它相当于一个偶极子,它是发射电磁波的理想振源。
下图就是一个偶极子振源发射的电磁波的电场部分。
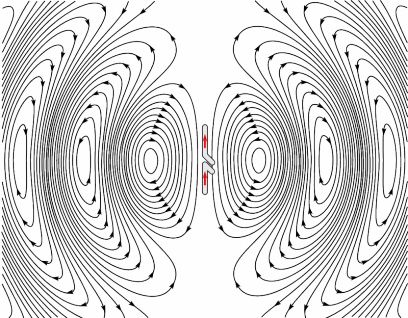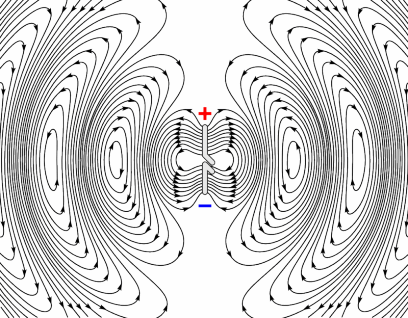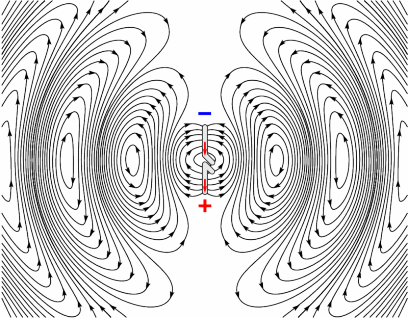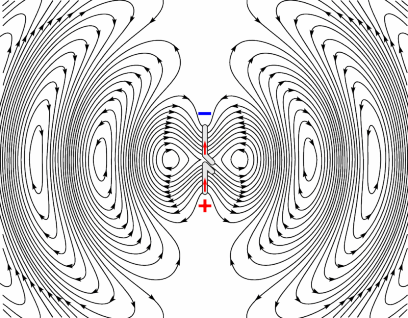
磁场线比电场线简单,它是处在与电场线垂直的平面(平行于偶极子的中垂面)内的一系列同心环,如下图中所示(点和叉)。
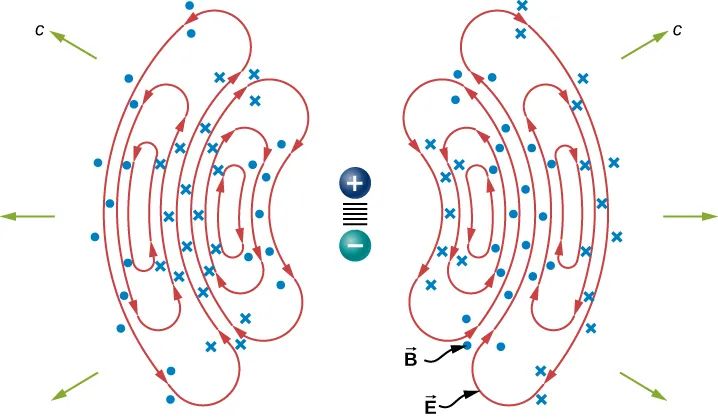
可以看到,磁场与电场都与该点的径向垂直,这正是横波所具有的特点。
类似于加速电荷的情形,当离偶极子非常远时,电磁波也趋于平面波简谐波。
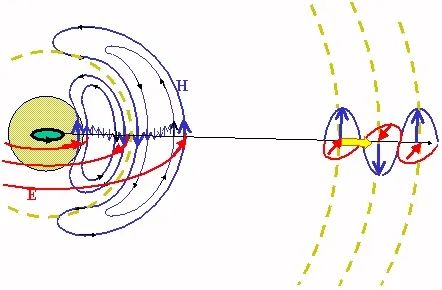
有人可能想问:光不就是电磁波吗?为什么要费这么大劲去发射?
答曰:因为光不是典型的电磁波,不能满足实际应用的需要。
可见光的频率都高达数十万GHz,产生这么高频率的电磁波只能凭借天然的电磁波发射器——原子和分子,也是光源。并且,光源发光可没法用电磁学解释,必须用量子力学才行。
另外,上面得到电磁波的过程中,有一个细节问题需要提示一下:只有在远离电荷或偶极子的地方——波场区,才能得到上面那种电磁波的结果。因为靠近电荷的地方,需要考虑其他的电场和磁场,情况比较复杂。
还需要指出的一个问题是,我们假设电荷作简谐振动,才得出电磁波具有简谐波的形式。但实际上如果电荷作其他加速运动,电磁波可以是非简谐波。
但无论电荷怎样加速度运动,在远离电荷的波场区,电磁波最基本的组分必定都是简谐波。为什么呢?因为根据傅里叶定理,任何加速运动都可以看作是简谐振动的叠加(参看文章“为什么简谐振动是最基本的振动?”),这样的话,每个简谐振动所对应的电磁波必然还是简谐波。
当然,这一点也可以从麦克斯韦电磁波理论得到证实——下面马上就来了!
到此,本文的主要任务已经完成了。
但是,恐怕有人不满意,因为很多人听说了:电磁波是麦克斯韦方程组的结果!
没错,基于麦克斯韦方程组,我们可以很好的理解磁生电、电生磁的涵义,并从理论上推得电磁波。当年麦克斯韦就是这么干的。直到他去世后9年,德国的物理学家赫兹才通过实验证实了电磁波的存在。

Heinrich Hertz
其实,从麦克斯韦方程组推导电磁波,几乎是一个纯数学问题。只要你的数学足够好,考虑到自由空间没有电荷和电流,你可得到如下方程
根据麦克斯韦方程组,你能得到电磁波的所有性质和规律,它们构成了整个电磁波理论。

END
