信号带宽是信号频谱的宽度,也就是信号的最高频率分量与最低频率分量之差,譬如,一个由数个正弦波叠加成的方波信号,其最低频率分量是其基频,假定为f=2kHz,其最高频率分量是其7次谐波频率,即7f=7×2=14kHz,因此该信号带宽为7f-f=14-2=12kHz。信道带宽则限定了允许通过该信道的信号下限频率和上限频率,也就是限定了一个频率通带。比如一个信道允许的通带为1.5kHz至15kHz,其带宽为13.5kHz,上面这个方波信号的所有频率成分当然能从该信道通过,如果不考虑衰减、时延以及噪声等因素,通过此信道的该信号会毫不失真。然而,如果一个基频为1kHz的方波,通过该信道肯定失真会很严重;方波信号若基频为2kHz,但最高谐波频率为18kHz,带宽超出了信道带宽,其高次谐波会被信道滤除,通过该信道接收到的方波没有发送的质量好;那么,如果方波信号基频为500Hz,最高频率分量是11次谐波的频率为5.5kHz,其带宽只需要5kHz,远小于信道带宽,是否就能很好地通过该信道呢?其实,该信号在信道上传输时,基频被滤掉了,仅各次谐波能够通过,信号波形一定是不堪入目的。通过上面的分析并进一步推论,可以得到这样一些结果:
如果信号与信道带宽相同且频率范围一致,信号能不损失频率成分地通过信道;
如果带宽相同但频率范围不一致时,该信号的频率分量肯定不能完全通过该信道(可以考虑通过频谱搬移也就是调制来实现);
如果带宽不同而且是信号带宽小于信道带宽,但信号的所有频率分量包含在信道的通带范围内,信号能不损失频率成分地通过;
如果带宽不同而且是信号带宽大于信道带宽,但包含信号大部分能量的主要频率分量包含在信道的通带范围内,
如果带宽不同而且是信号带宽大于信道带宽,但包含信号大部分能量的主要频率分量包含在信道的通带范围内,通过信道的信号会损失部分频率成分,但仍可能被识别,正如数字信号的基带传输和语音信号在电话信道传输那样;
如果带宽不同而且是信号带宽大于信道带宽,且包含信号相当多能量的频率分量不在信道的通带范围内,这些信号频率成分将被滤除,信号失真甚至严重畸变;
不管带宽是否相同,如果信号的所有频率分量都不在信道的通带范围内,信号无法通过;
不管带宽是否相同,如果信号频谱与信道通带交错,且只有部分频率分量通过,信号失真。另外,我们在分析在信道上传输的信号时,不能总是认为其带宽一定占满整个信道,比如频带传输;即使信号占据整个信道,也不一定总是把它想像成一个方波,它也可能是其它的波形,比如在一个单频的正弦波上寄载其它模拟信号或数字信号而形成的复合波形。
带宽这个词是学习电子和通信经常能够看到的词。可是在不同的应用场合有不同的含义。经常听到有人抱怨,我就测一个50MHz的信号,用100MHz的示波器测出来怎么波形变形这么大。其实很多时候不是示波器的问题,这是信号带宽的事。
说信号带宽就先说说频域吧。频域这词大家也经常听到了。所有的时域信号经过傅立叶变换就可以在频域中表示出来。频域就是一个人为创造出来的实际不存在的域。在这个域里只存在正弦波,没有其它东西。时域中真实存在的信号经过傅立叶分解被分解成不同频率和幅度的正弦波分量,可以在频域中表示出来。正弦波是最干净的信号,每个正弦波在频域中就是一个点。其它实际信号的频谱都是“不干净”的,包含很多的频率分量。那么实际信号在频域里最高的那个频率分量就被称为信号的带宽。让我们看看一个理想的100MHz的理想方波带宽是多少。很遗憾通过傅立叶变换,理想方波有n个谐波分量。难道理想方波的带宽是无穷大?如果非要这么说,也没错,不过这对我们的实际工作没有任何指导意义。于是人们通过大量的试验总结发现:信号的绝大部分能量都集中在信号的前几次谐波分量当中。方波,是一个频谱分量众多的信号,其包括了基波和高次谐波。它可以由很多个正弦波叠加而成。而示波器的带宽是有限的,所以使用示波器观察方波时,如果带宽不够,会把高次的谐波滤掉,方波看起来就像正弦波了。
总结了信号带宽与上升时间的关系:BW=0.35/TrBW为信号带宽位为GHz,Tr是上升时间单位为ns。我们来看看一个上升时间是10ns的信号,通过公式计算信号带宽是35MHz,而一个上升时间为1ns的信号,信号带宽就是350MHz。那么第一个信号我们就可以用100MHz的示波器来测量,而第二个信号用同一个示波器测试会有很大的失真。这里我们说的是上升时间不是频率。也就是说如果同样是一个50MHz的信号,上升时间不同,信号带宽是不同的。但是实际当中我们更多情况下是不知道上升时间而只知道信号频率的。怎么办?那就近似推导吧。一般ASIC芯片的接口信号,上升时间大约是信号周期的百分之7。根据这个关系,代入上面的公式就可以得到带宽和频率的关系。BW=5f。f是信号频率。这样,一个50MHz的信号,我们最好能用一个250MHz带宽的示波器来测量,才能得到一个很好的结果。
信号带宽和信号频率的关系BW=0.35/RT=5f一般普通信号的Tr=7%*T,其中:T=1/f)。实际信号的带宽:信号谐波幅值将为0次波(基波)的70%(即下降3dB)时的谐波频率。如果你测试的是一个理想的50MHz正弦波,用100MHz带宽的示波器够用么?
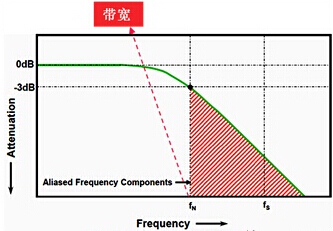
示波器带宽是示波器的首要指标,和放大器的带宽一样,是所谓的-3dB点,即:在示波器的输入端加正弦波,幅度衰减至-3dB(70.7%=0.707)时的频率点就是示波器的带宽。
简单的定义是:示波器测得正弦波的幅度不低于真实正弦波信号3dB 的幅度时的最高频率
根据电压幅度计算:20log(0.707)=-3dB
根据功率计算:10log(0.5)=-3dB
如果我们用100MHz带宽的示波器测量:幅值为1V ,频率为100MHz 的正弦波时,实际得到的幅值会不小于0.707V。
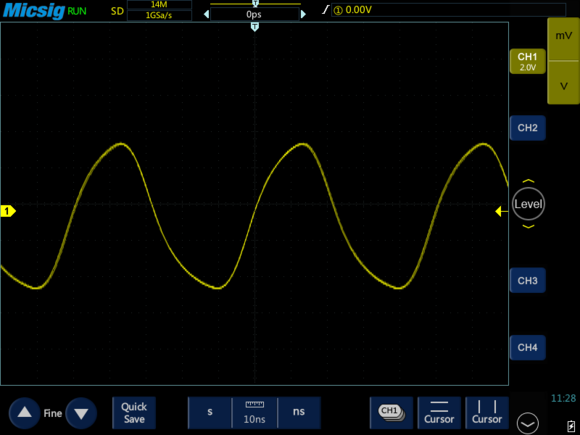
那么作为示波器的首要参数指标,“带宽不足”对波形测量有哪些影响呢 ?我们用20M、60M、100M带宽的示波器分别观察20M的方波信号 。
20M示波器
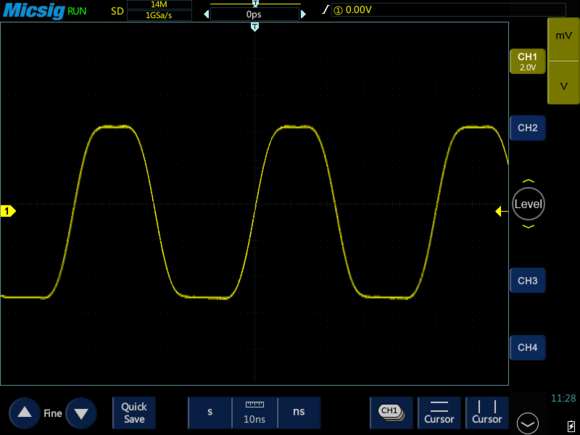
60M示波器
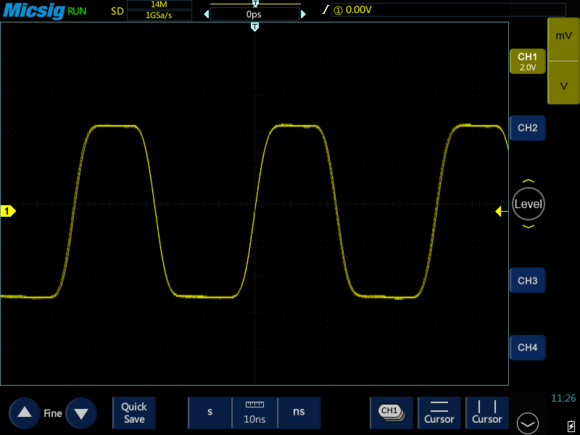
100M示波器
由上面三张图可以看出:
20M示波器基本无法观察到方波形状,另外100M示波器的观察效果比60M示波器要好,下面我们来一起分析原因:
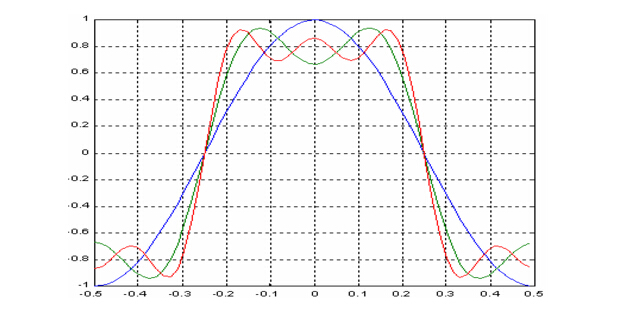
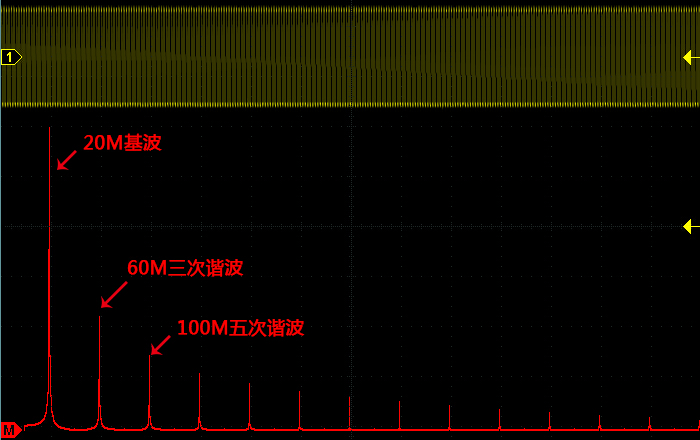
上图中,我们可以看到方波是由基波以及3、5、7、9……次谐波分量递加而成。所以20M的方波包含20M基波、60M三次谐波,100M五次谐波,140M七次谐波……如果要对波形进行准确测量,应该让示波器的带宽大于波形的主要谐波分量。因此对于正弦波可以要求示波器的带宽大于波形的频率,但是对与非正弦波则要求示波器的带宽大于波形的最大主要谐波频率。
带宽不足具体的影响表现在以下两个方面:
1、由低带宽导致主要谐波分量消失,使原本规则的波形呈圆弧状接近正弦波;
2、低带宽给波形的上升时间和幅度的测量带来较大的误差。
所以示波器的带宽越高,实际测量也就越精确,当然价格和成本也会更高,那么我们需要多大带宽的示波器才合适呢?一般所测信号最大频率的5倍,就是最合适的带宽,即带宽的5倍法则。使用示波器测量信号的通用法则是:示波器的带宽是被测信号的频率的5 倍。示波器带宽指的是正弦输入信号衰减到其实际幅度的70.7%时的频率值,带宽决定着示波器对信号的基本测量能力,随着信号频率的增加,示波器对信号的准确显示能力将下降。如果没有足够的带宽,示波器将无法分辨高频变化,幅度将出现失真,边缘将会消失,细节数据将被丢失,得到的关于信号的所有特性都是没有意义的方波,是一个频谱分量众多的信号,其包括了基波和高次谐波。它可以由很多个正弦波叠加而成。而示波器的带宽是有限的,所以使用示波器观察方波时,如果带宽不够,会把高次的谐波滤掉,方波看起来就像正弦波了。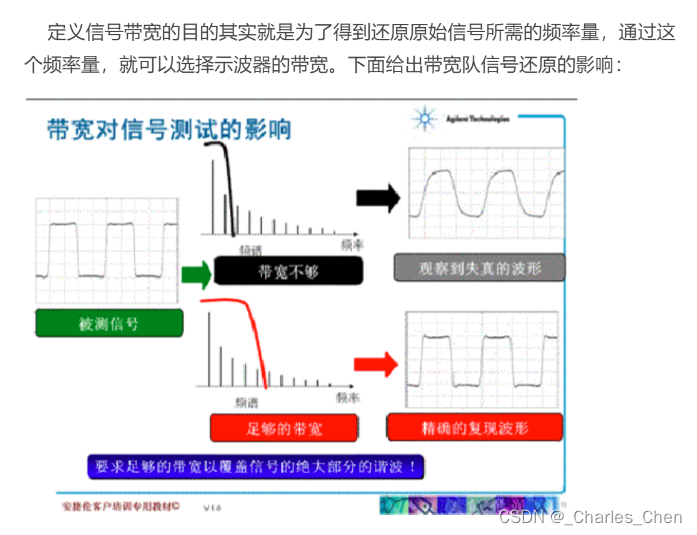

带宽是示波器最重要的指标之一。
模拟示波器的带宽是一个固定的值,数字示波器的带宽有模拟带宽和数字实时带宽两种。数字示波器对重复信号采用顺序采样或随机采样技术所能达到的最高带宽为示波器的数字实时带宽,数字实时带宽与最高数字化频率和波形重建技术因子K相关(数字实时带宽=最高数字化速率/K),一般并不作为一项指标直接给出。从两种带宽的定义可以看出,模拟带宽只适合重复周期信号的测量,而数字实时带宽则同时适合重复信号和单次信号的测量。厂家声称示波器的带宽能达到多少兆,实际上指的是模拟带宽,数字实时带宽是要低于这个值的。常见的数字存储示波的采样率单位是1GSa/s,代表什么含义? 是每秒采样1G个点。但是,数字示波器的采样率不是固定不变的,随着你的屏幕分辨率不同,其每秒采样的次数也不同。1G是指采样的最大值。
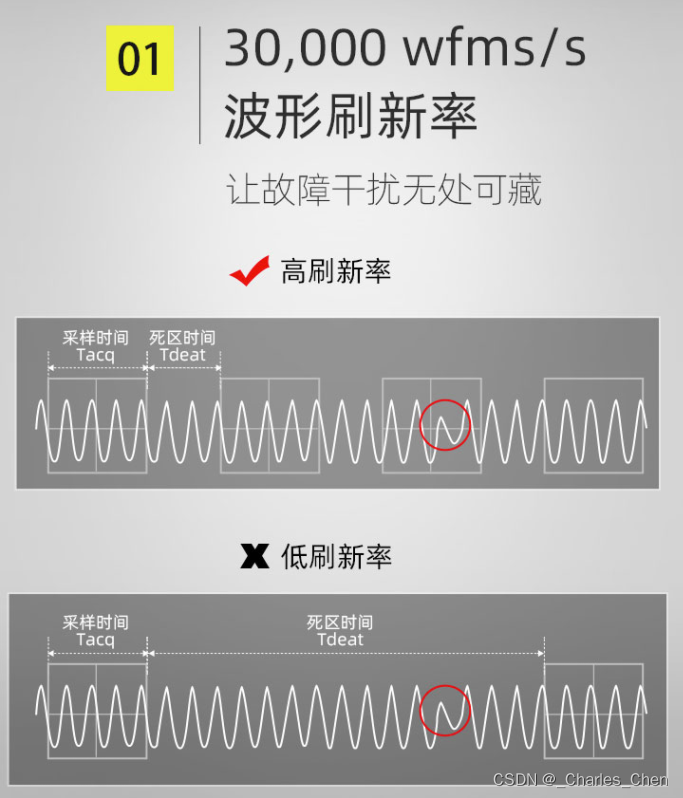
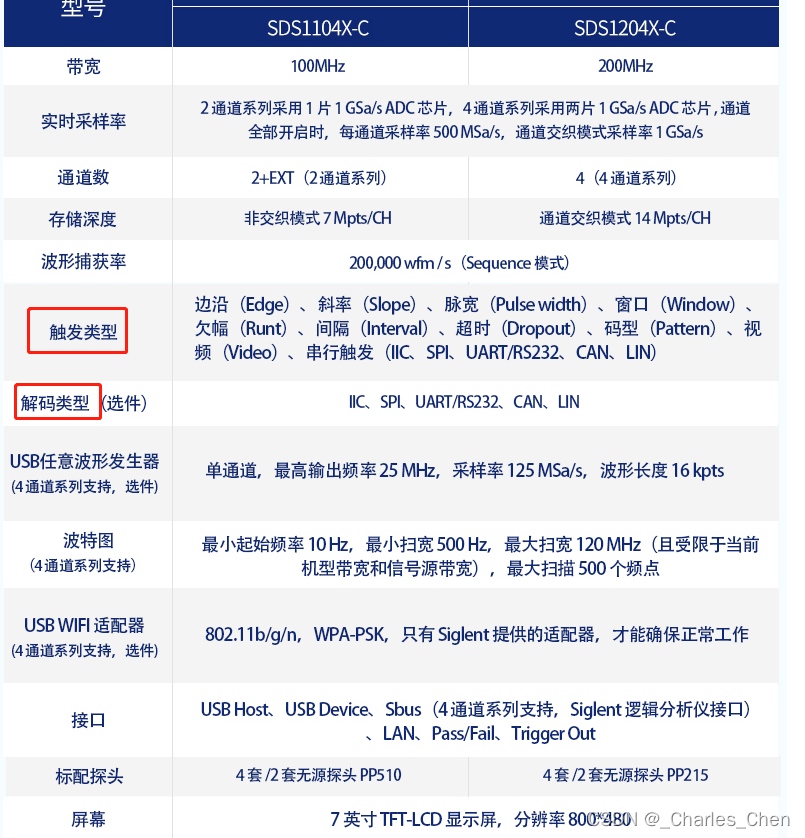
500,000 wfm/s =50万帧/秒,代表短的死区时间,更大概率的快速捕获异常事件,让故障干扰无处可逃
高端就是泰克,力科,是德Keysight(原安捷伦),横河,安立,罗德
国内一级:鼎阳,普源RIGOL,固纬
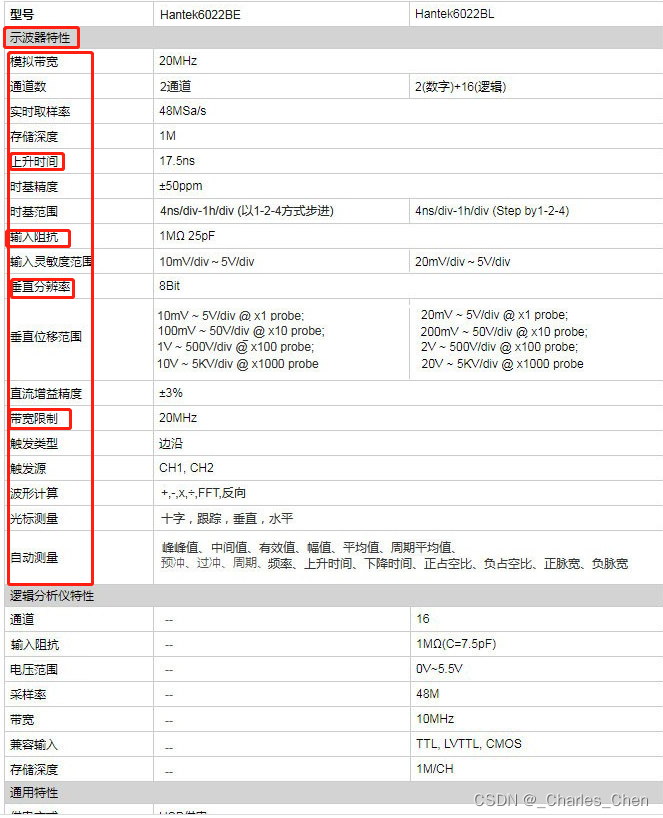
国内二级:汉泰Hantek,胜利Victor,利利普,优利德

本号对所有原创、转载文章的陈述与观点均保持中立,推送文章仅供读者学习和交流。文章、图片等版权归原作者享有。投稿/招聘/推广/宣传 请加微信:15989459034