
来源 | 雷达信号处理matlab
智库 | 云脑智库(CloudBrain-TT)
云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向
声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(15881101905,微信同号)删除,谢谢。
雷达信号模糊函数(Ambiguity Function)全面地反映了雷达所发射的信号在距离(时间)和速度(频率)两个维度上的测量精度和分辨率,它可以提供分辨力、测量精度和杂波抑制等重要信息。下图为模糊函数图像。
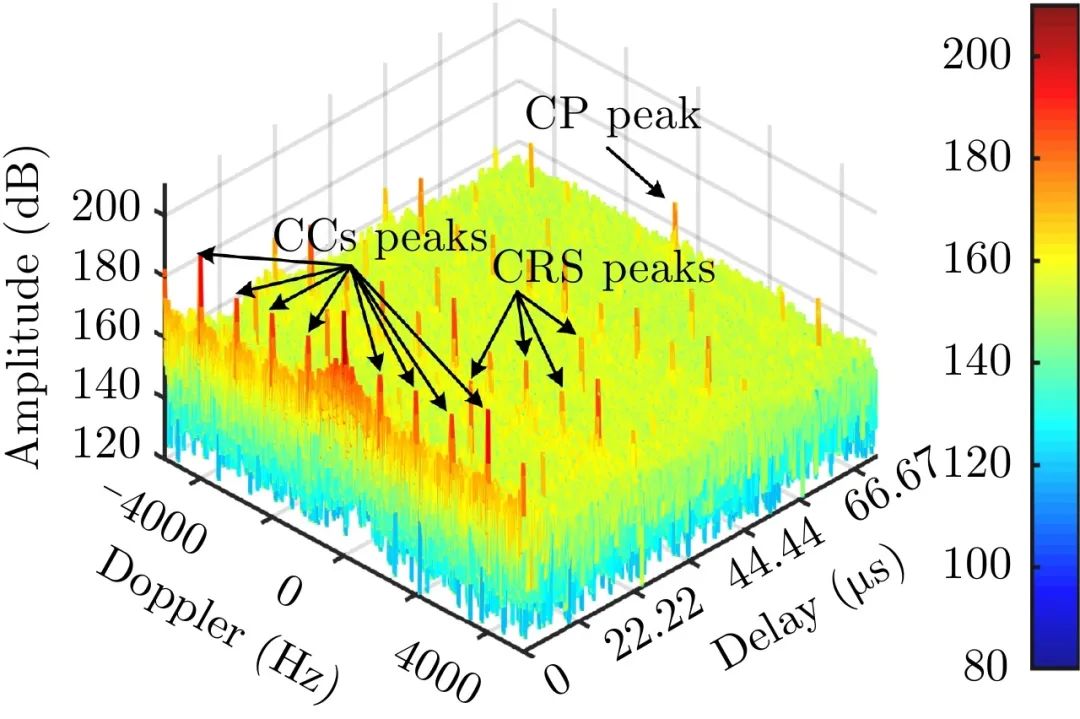
图片源自网络
模糊函数可以作为单一目标距离和速度的精度与分辨率评估尺度参数,根据这些参数还可以可靠区分多个目标。
模糊函数的来源
模糊函数最早是维莱(J.Ville)于 1948 年提出的,由于伍德沃尔德进行了先驱的开拓工作,故又称伍德沃尔德模糊函数。
雷达波形设计不仅决定了信号处理方法,而且直接影响系统的分辨率、综合的重要内容。故人们希望找到一种“理想”的波形,以适应各种不同的目标环境和工作要求,很快就发现这种努力是徒劳的。
雷达波形设计一直沿着不同的途径进行研究:
波形综合道路,通过模糊函数最优综合的方法,得到所需的最优波形。但这方面不仅遇到了数学上的困难,而且综合得到的复杂调制波形,也往往是技术上难以实现的信号。
简要的波形设计途径,即根据目标环境图和信号模糊匹配的原则,选择合适的信号类型。进而兼顾技术实现的难易程度,选择合适的信号形式和波形参数。
现代先进的数字化多功能雷达大多采用多发射信号,以适应不同的战术用途。
雷达中通常使用的接收机滤波器称作匹配滤波器(详见#匹配滤波器讲解#)。这种滤波器在噪声是相加的高斯白噪声时信噪比最大,因而提供最大的目标检测能力。下图为高斯白噪声图像。
图片源自网络
胡德瓦特把脉冲压缩和匹配滤波器的概念归并成一个有用的函数,这个函数就是模糊函数。这个函数描述雷达信号的分辨特性、测量精度等特性。即使从理论上讲,也不存在对所有用途都理想的雷达波形。
因此,某些雷达能发射几种不同的波形,每一个波形适应不同的用途。对一种给定的情况来讲,波形设计要求知道雷达要获得的信息和要排除的信息。要获得的信息可能包括:距离、径向速度、雷达截面积、目标回波频谱、幅度和相位,以及极化特性。设计还要求知道所需的数据率和测量精度。确定要排除的信息就要知道影响分辨力的有关知识。
模糊函数的定义
模糊函数最初是为了研究雷达分辨率而提出的,目的是通过这一函数定量描述当系统工作于多目标环境下,发射一种波形并采用相应的滤波器时,系统对不同距离、不同速度目标的分辨能力。
换句话说,就是当“干扰目标”与观测目标之间存在着距离和速度差时,模糊函数定量地表示了“干扰目标”(即临近的目标)对观测目标的干扰程度。
下面从分辨两个不同的目标出发,如下图所示,以最小均方差为最佳分辨准则,推导模糊函数的定义式。
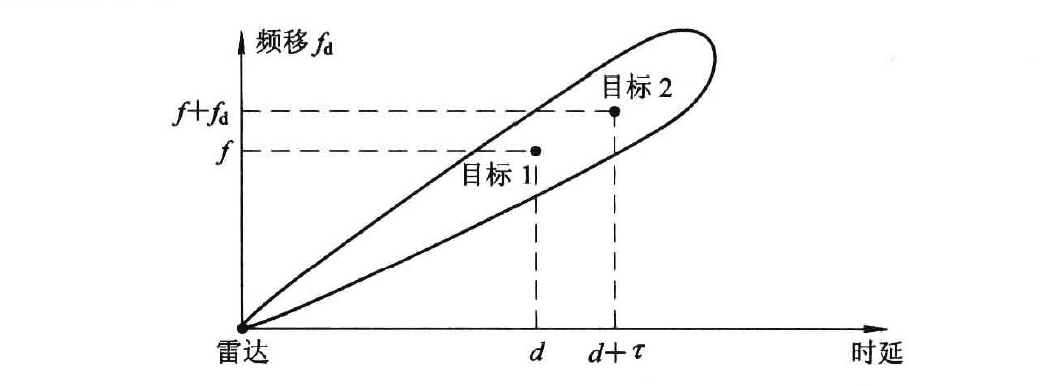
雷达的发射信号通常为窄带信号,用复信号可表示为
假设目标 1 和目标 2 的功率相同,则时延为
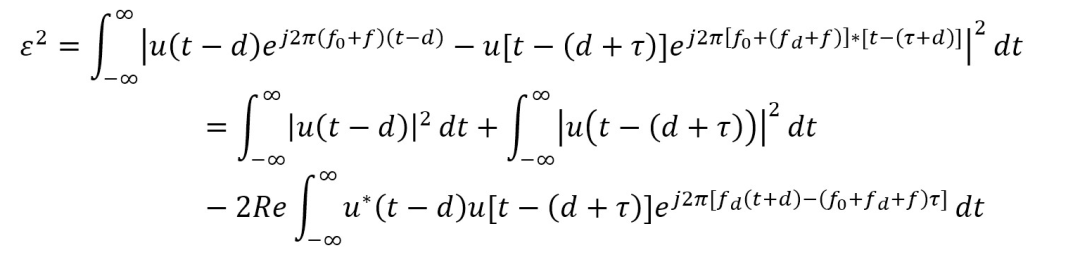
作变量代换,令
需要说明的是,上式并不是模糊函数的唯一形式。有的文献从匹配滤波器的输出出发,定义了不同形式的模糊函数
在没有噪声的情况下,最优滤波器的输出为模糊函数图的再现,不同之处只是峰值点不在原点,对应的时延与频移发生了偏移。模糊函数图的峰值在原点;对目标回波而言,最优滤波器输出的峰值对应的位置为目标的距离和多普勒频率。
一般匹配滤波器的输出都经过线性检波器取出包络值,所以
利用帕斯瓦尔(Parseval)定理及傅立叶变换性质,
图片源自网络
为方便起见,有时也常用模糊度图来表示模糊函数,它是幅度归一化模糊函数图在某一高度上(如
本文参考《雷达原理(第三版)》,有兴趣的可以购买书本帮助理解。
上期我们介绍了两个回波信号的均方差为
由回波信号的均方差可知,
本期我们将介绍模糊函数的一些重要性质:
关于原点的对称性
在原点取得最大值
该性质的意义在于:模糊函数的最大值点也就是差平方积分准则的最小点,即最难分辨点。这样的点是两个目标在距离和径向速度上都没有差别的点,即
模糊体积不变性
但这并不是说雷达信号不需要进行设计,虽说其总的体积不变,但信号的形式不同,模糊图的分布不同(即二维分辨率不同)。
我们可以根据目标的环境,选取适当的信号形式,在所需要分辨目标的区域,使模糊图的体积小一些,而在不需要分辨的区域,模糊图的体积大些,以此来提高分辨率。
自变换特性
雷达分辨理论
雷达分辨率是指在各种目标环境下区分两个或两个以上的邻近目标的能力。雷达分辨邻近目标的能力主要从距离、速度、方位和仰角四个方面考虑,其中方位和仰角的分辨率取决于波束宽度。
一般雷达难以在这四维同时能分辨目标,在其中任意一维能分辨目标就认为具有目标分辨的能力。这里主要分析距离分辨率和速度分辨率与波形参数的关系,通过分辨常数和模糊函数来分析各种波形的分辨性能。
距离分辨率
假定相邻两目标在同一方向的不同距离上,在不考虑相邻目标多普勒频移时,由信号模糊函数可得
当
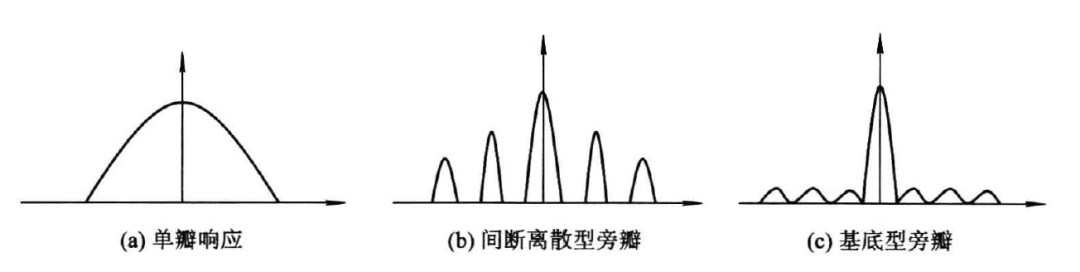
图(a)的响应是单瓣的,但如果主瓣很宽,临近目标就难以分辨。
图(b)的响应主瓣很窄,对临近目标的分辨能力较好,但存在间断离散型旁瓣,若其间距为
图(c)的响应主瓣也很尖,但存在类似噪声的基底型旁瓣;虽然基底旁瓣不高,但强目标的响应基底有可能掩盖弱目标的响应主瓣;在多目标环境中,多个目标响应基底的合成甚至可能掩盖较强目标的主瓣,造成临近目标不能分辨。
正因为如此,至今尚没有统一的反映信号分辨特性的参数。通常用距离模糊函数和速度模糊函数主瓣的
名义分辨率(nominal resolution)只表示主瓣内邻近目标的分辨能力,而没有考虑旁瓣干扰对目标分辨的影响。有时为了方便,如遇到
时延分辨率为
当目标时延差较大时,为了全面考虑主瓣和旁瓣的分辨问题,可以定义另一种反映分辨特性的参数:时延分辨常数
显然,从距离分辨角度出发,信号距离模糊函数的最佳形式是冲击函数。因此可用模糊函数与冲击函数的相似程度来衡量信号的固有分辨率,它表示信号频谱与均匀谱的相似程度,称为频谱持续宽度
因此,只要信号具有大的持续带宽(有效相关带宽)就能获得高的距离分辨率,而不必具有很窄的脉冲宽度(窄脉冲信号限制辐射的能量)。
速度分辨率
与距离分辨率类似,信号的速度分辨率取决于速度模糊函数
距离—速度联合分辨率
如前所述,速度相同、距离不同的目标分辨用信号的距离模糊函数表示;距离相同、速度不同的目标分辨用信号的速度模糊函数表示。类似地,可以用
定义模糊面积
由模糊函数性质可知,只要信号的能量一定,模糊面积即为定值。这就说明了时延与多普勒联合分辨率的限制。
无论怎样使时延
本文参考《雷达原理(第三版)》,有兴趣的可以购买书本帮助理解。
前面我们介绍了模糊函数的定义以及相关性质,接下来我们将介绍如何使用模糊函数来分析波形。比较几种基本波形的距离和多普勒分辨能力,例如矩形波形和线性和步进 FM 波形。
在雷达系统中,波形的选择对于系统在距离或速度上分辨两个靠近的目标具有重要作用。因此,有必要了解不同波形其在距离和速度域中的分辨率和模糊度。
为了提高信噪比(SNR),现代雷达系统通常在接收机中使用匹配滤波器。当指定的波形输入滤波器时,波形的模糊函数能准确地表示匹配滤波器的输出。假设目标的 RCS(目标雷达截面积)相等时,模糊函数可描述为与参考目标有不同距离和速度的一个点目标回波引起的干扰的大小。
模糊函数在
这种精确的表示提供了对给定波形的时间延迟域和多普勒域分辨率能力的洞察。根据这一分析,然后可以确定波形是否适合特定应用。
矩形脉冲信号的模糊函数
矩形脉冲信号的归一化包络可写为
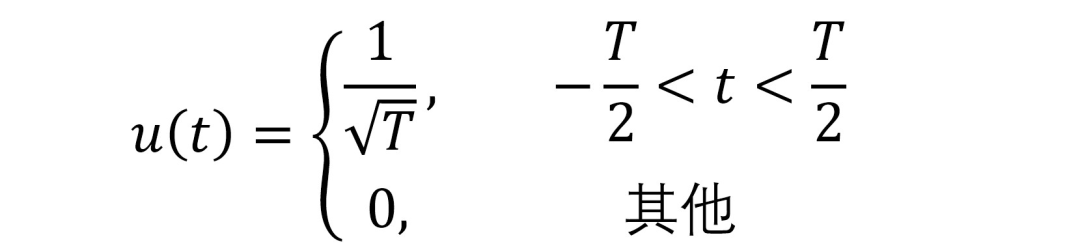
其中
①当
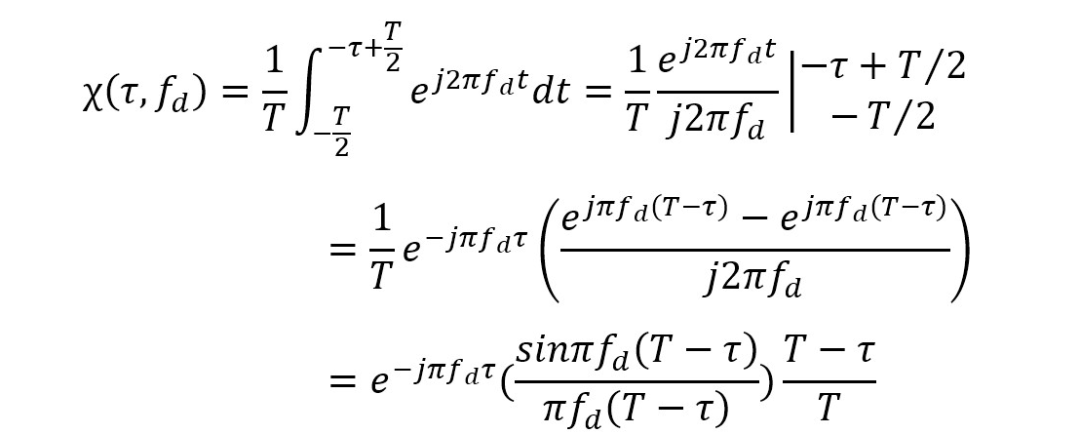
②当
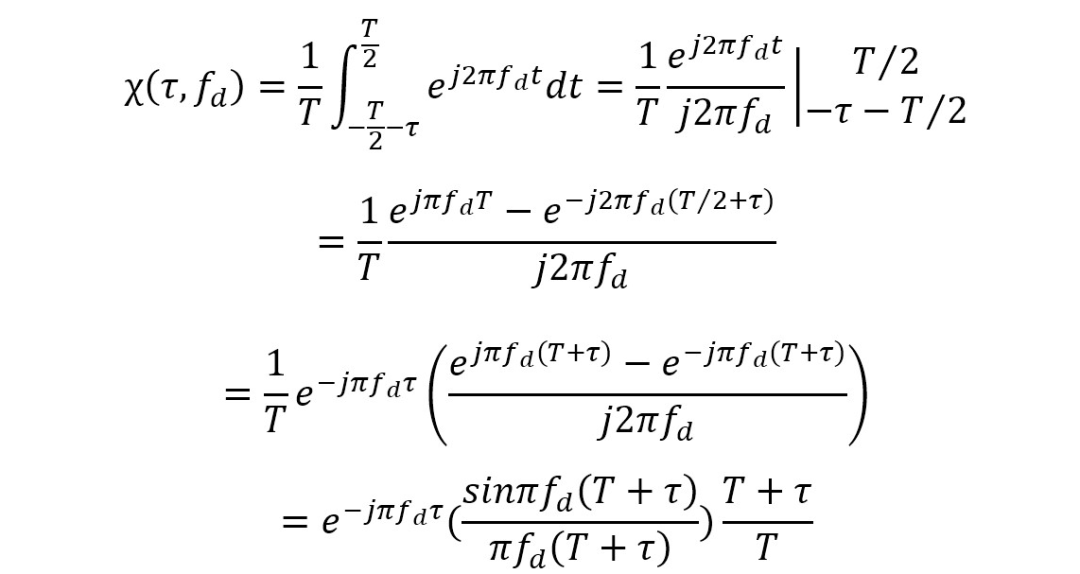
③当
综上所述,可得
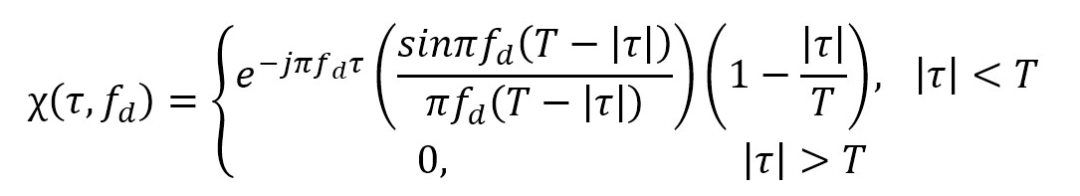
所以,矩形脉冲信号的模糊函数可表示为
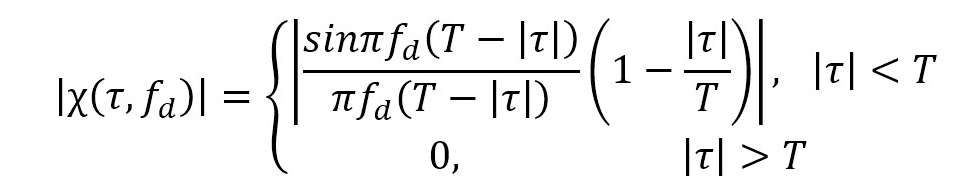
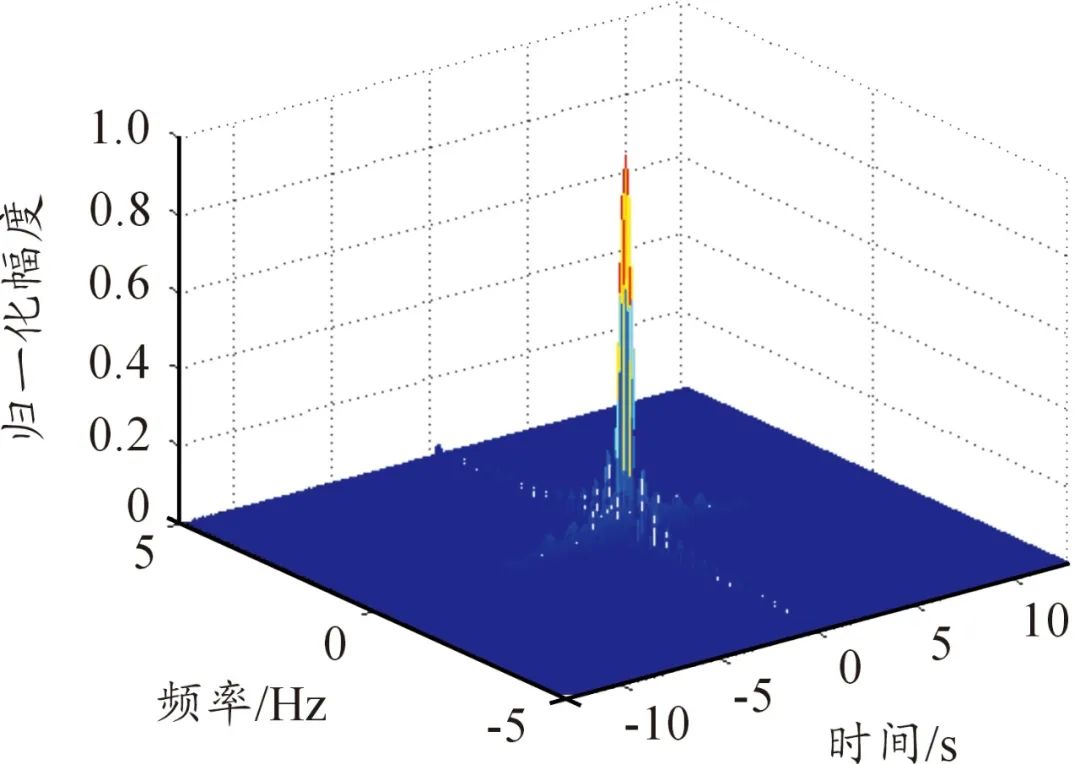
故矩形脉冲信号的模糊函数如下图所示(脉宽

其模糊度图如下图所示。
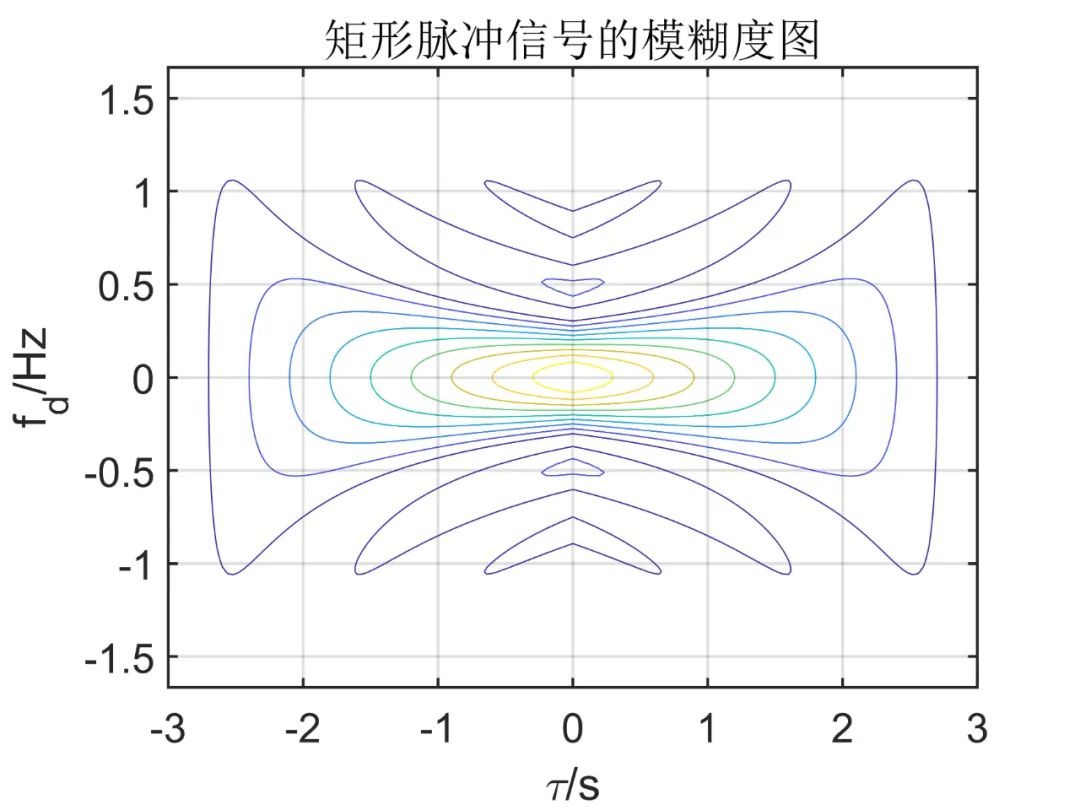
若令
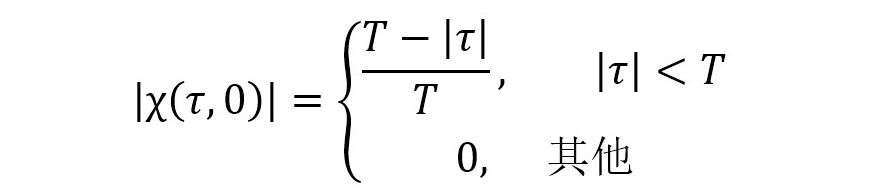
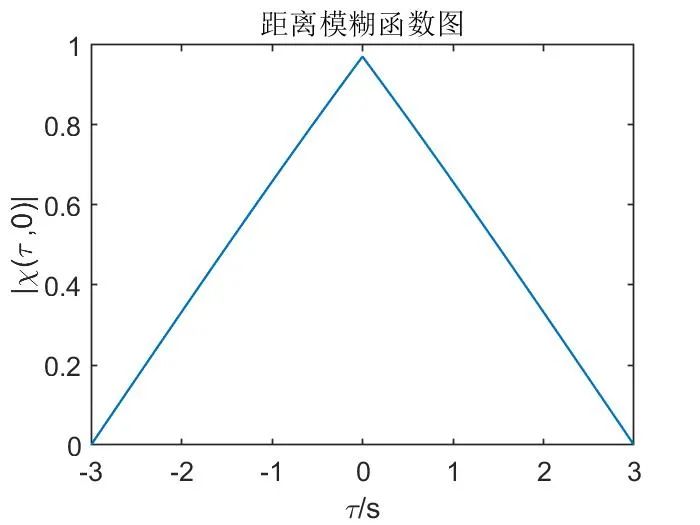
如下图仿真结果所示,可以看到
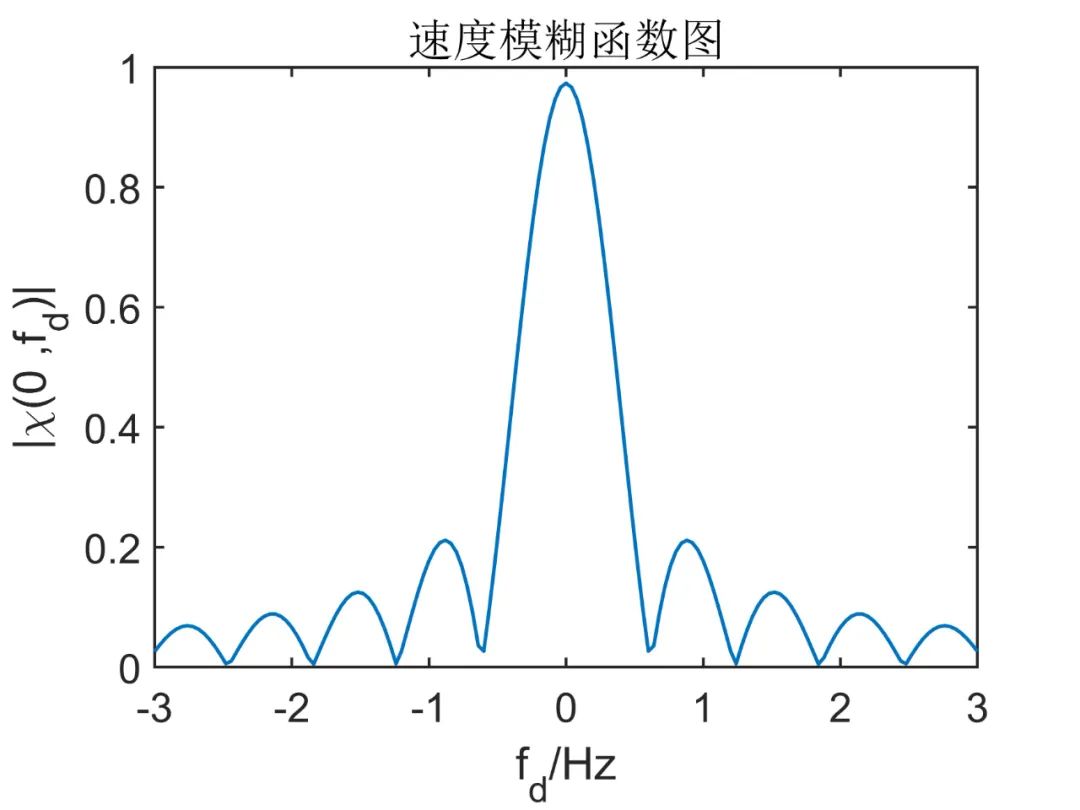
同理,令
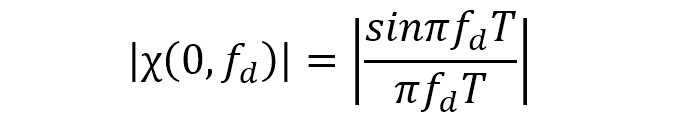
当
下图表示不同脉宽的矩形信号的模糊度图(-6dB),从图中我们可以看出,单个脉冲模糊度图是一个椭圆区,在该区域中
可以看出,宽脉冲有良好的频率测量精度(在频率方向模糊范围小),但其时延精度较差(在时延方向模糊范围大),而窄脉冲有相反的结果。
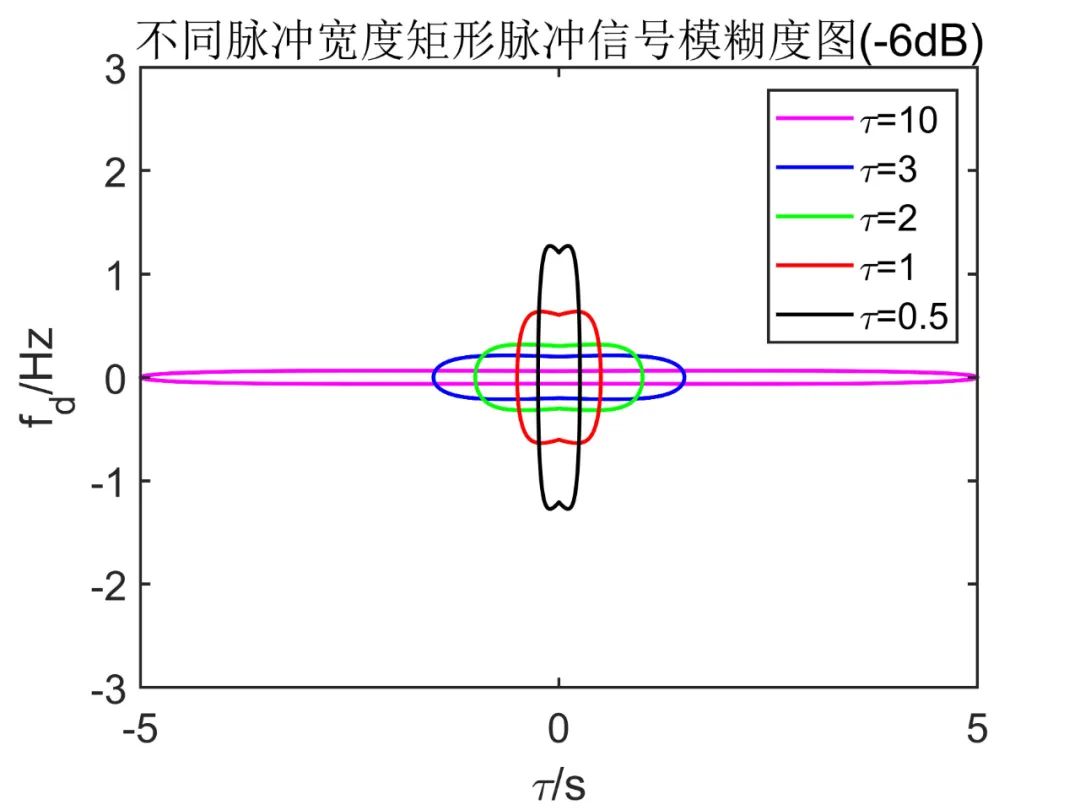
该图表明,当简单脉冲波形的距离精度改善时,频率精度就会变差,反之亦然(这可由模糊函数体积不变的性质决定的)。不能同时获得较好的距离和速度分辨力,距离分辨力与距离探测性能是矛盾的。
窄脉冲具有多普勒容错性,即如果有严重的多普勒频移,则单个匹配滤波器会产生良好的输出,也就是说,当有多普勒频移时,与零多普勒频移相匹配的滤波器输出不会有太大的变化。另一方面,由于多普勒频移,长脉冲将使输出减小很多,因此,它不具备多普勒容错性。
从前面的分析可以看出,单载频脉冲信号模糊图呈正刀刃形,其重要特征是模糊体积集中于与轴线重合的“山脊”上。窄脉冲沿频率轴取向,具有良好的距离分辨率;而宽脉冲沿时延轴取向,具有良好的速度分辨率。
单载频脉冲信号的不足之处是不能同时提供距离和速度参量的高分辨率。由于单脉冲信号的产生和处理都比较简单,因此对目标测量精度以及多目标分辨率要求不高、作用距离又不太远的雷达,可采用此类信号,实际上这也是一般雷达最常用的一种信号形式。
- The End -
版权声明:欢迎转发本号原创内容,转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系删除。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/入群/赞助 请加微信:15881101905,备注关键词

“阅读是一种习惯,分享是一种美德,我们是一群专业、有态度的知识传播者.”
↓↓↓ 戳“阅读原文”,加入“知识星球”,发现更多精彩内容.
分享💬 点赞👍 在看❤️@以“三连”行动支持优质内容!