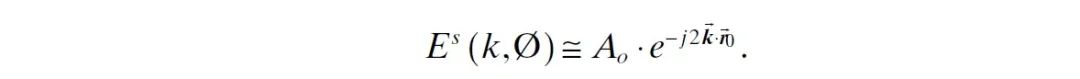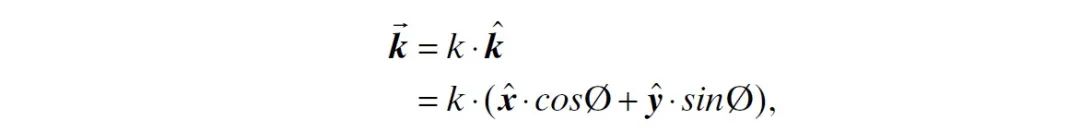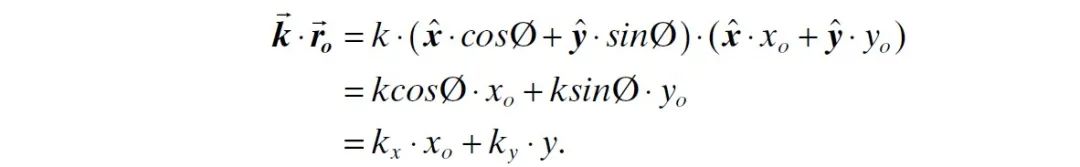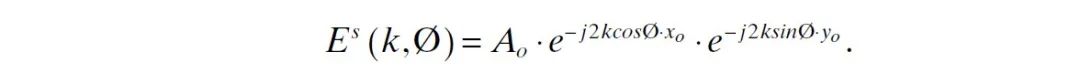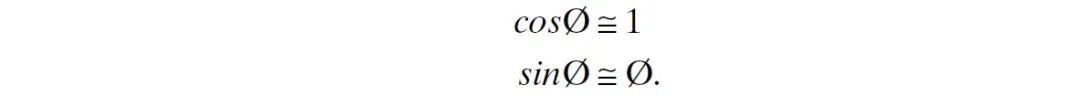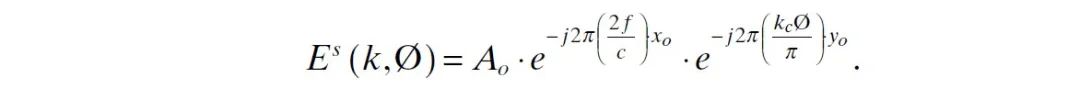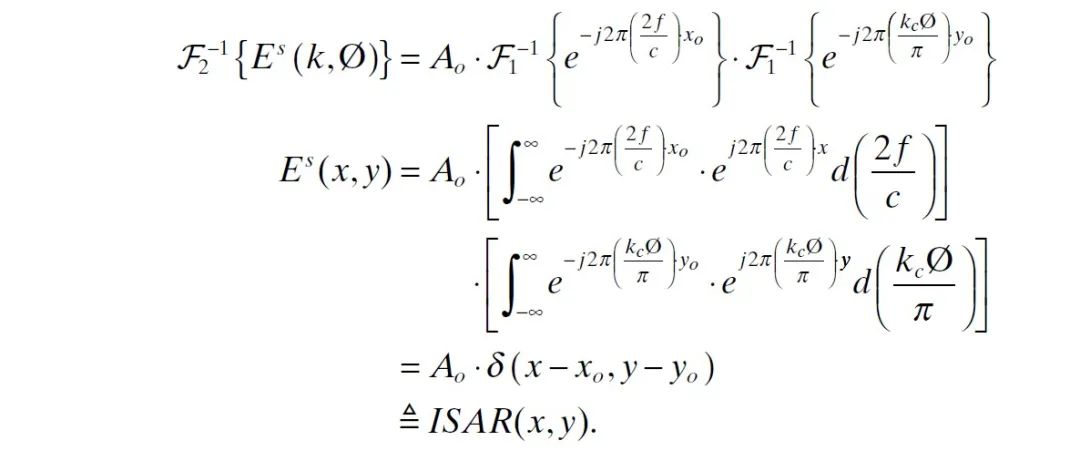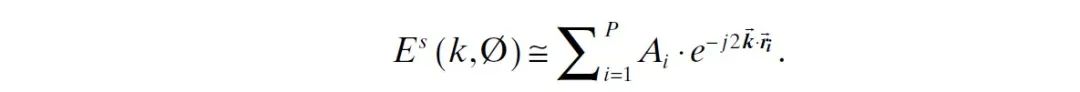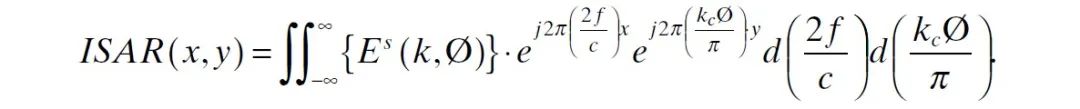在上期#散射场与 ISAR 成像#中,我们知道二维 ISAR 图像是一维方位像和一维距离像在平面上的显示。在本期中,我们简要介绍单基地 ISAR 的成像情况。
二维 ISAR 图像是在一个轴上显示距离像,在另一轴上显示方位像。因此应收集不同频率(距离像)、不同视角(方位像)下的散射场,如下图(a)所示,以便能够生成二维 ISAR 图像。
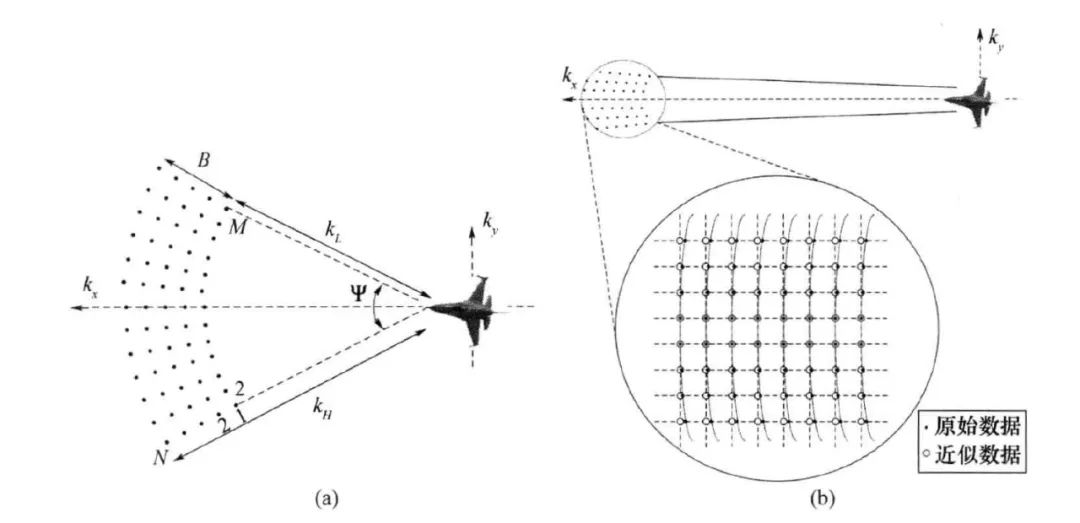
在该图中,假设波束矢量 位于二维空间频率域 平面上。如果收集的反向散射电场数据在有限的频率带宽 和有限的角度宽度 内,则二维数据在空间中占据非均匀网格。
但是,如果 和 都足够小,则 空间中的数据网格接近于等间距线性网格,如图(b)。这种情况使得可以利用快速傅里叶逆变换来形成 ISAR 图像。
本文讲述的二维 ISAR 成像算法是针对单基地情况提供的。假设点散射体 位于目标上,如下图所示。
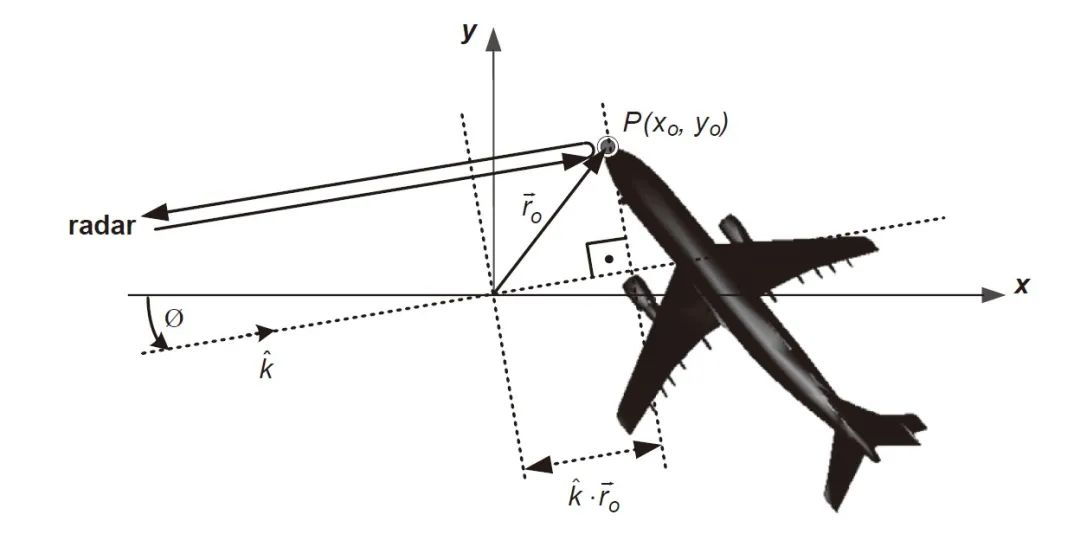
以原点为几何相位中心,在远场背景下,方位角为 处的点散射体的散射场可近似为
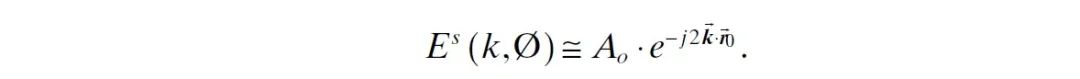
式中, 是散射场的幅度, 是传播方向上的波数矢量, 是从原点到点 的矢量。上式的相位滞后量为 。这是因为当电磁波到达点 并沿同一路径反射回来时,与到达原点的参考波相比,它将额外传播 的距离。
向量可以用 和 方向的波数表示
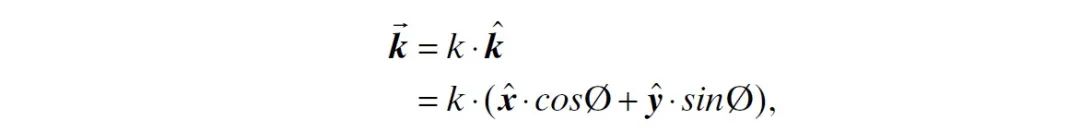
其中 、 和 分别是 、 和 方向上的单位向量。则
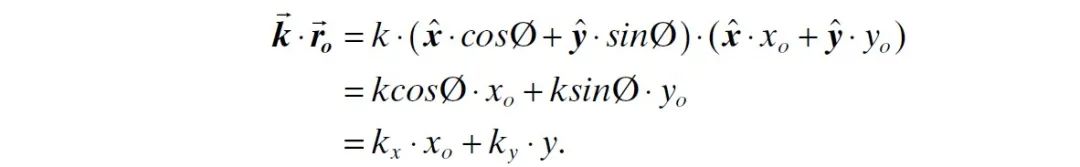
因此
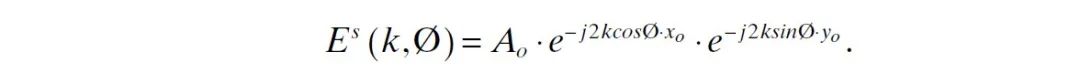
该式提供有两个独立的相位项,作为空间频率变量 和视角变量 的函数。
如果仔细检查这些相位项,可以很容易地注意到 和 、 和 之间的傅里叶关系。因此,对反射场做二维 IFT,可以在距离域和方位域中生成 ISAR 图像。
在实际的 ISAR 成像中,使用小的频率带宽 和小的视角变化范围 收集回波数据集,则称为小带宽小角度 ISAR 成像。在该成像过程中,频率带宽 比中心频率 小。实际上,小于中心频率十分之一的带宽就被认为足够小。
在小带宽小角度 ISAR 成像模式下,上式中第二相项中的波数可以近似为

其中 是对应于中心频率 的波数。视角变化范围 很小,则
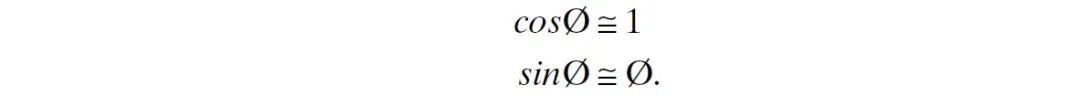
实际上, 到 的视角变化范围通常被认为是小的。此时 点的散射电场可以近似为

为了利用 FT,将上式变为
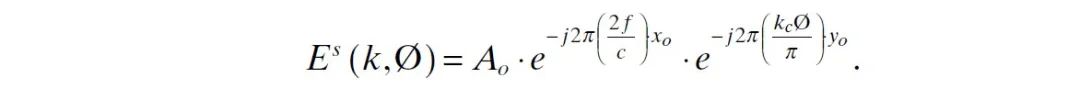
则 平面上的 ISAR 图像可以通过上式的二维 IFT 得到
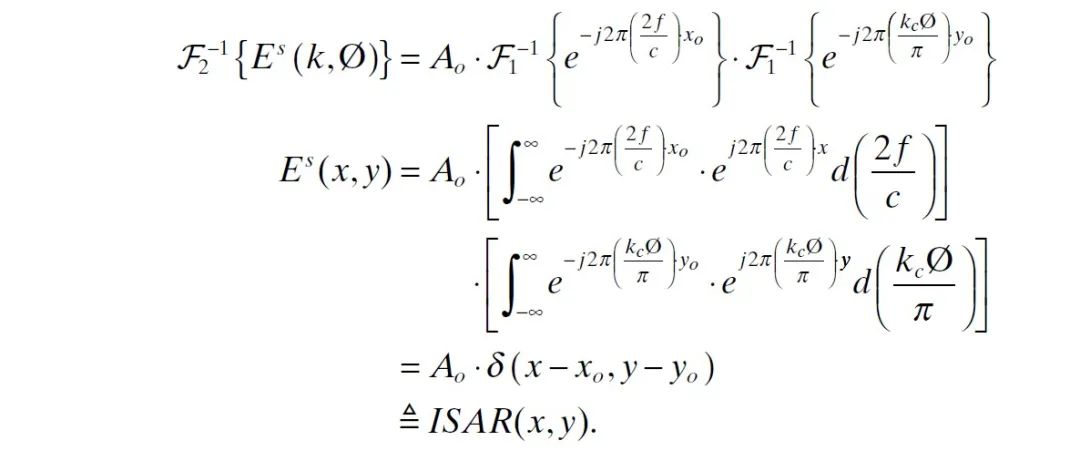
式中, 表示 平面上的二维脉冲函数。从上式可以看出,点 在 ISAR 图像中表现为位于 处且具有 幅度的二维脉冲函数。
来自目标的散射场可以近似为来自目标上有限数量的单点散射体(称为散射中心)的散射总和,如下所示:
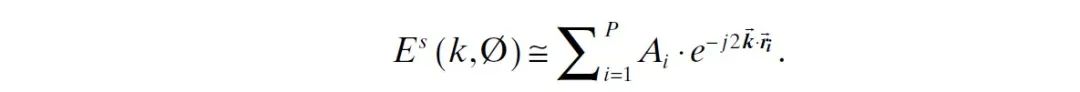
式中,来自目标的散射场近似为来自目标上 个不同散射中心的散射场的总和。 表示第 个散射中心的复后向散射场幅值, 称为从原点到第 个散射中心位置的位移矢量。
通过对二维后向散射场数据进行二维逆傅里叶变换,即可得到目标的 ISAR 图像
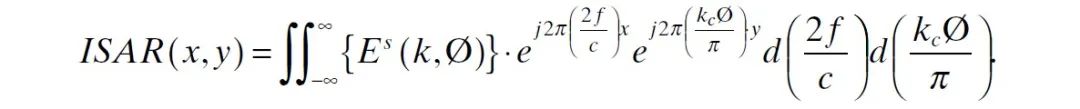
通过上述分析可知,小带宽小角度 ISAR 图像可以近似为

因此,得到的 ISAR 图像由 个散射中心及其电磁反射系数之和组成。上式中积分在实际中是有限的,因为只能在有限带宽和有限视角范围内收集现场数据。因此,实际的 ISAR 图像响应会从脉冲函数扭曲为 函数。