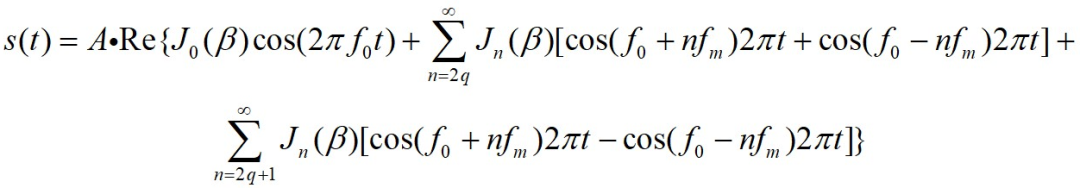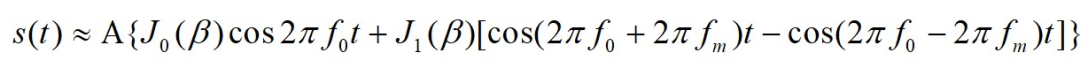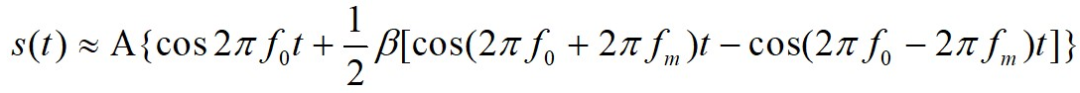来源 | 雷达信号处理matlab
智库 | 云脑智库(CloudBrain-TT)
云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向
声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(15881101905,微信同号)删除,谢谢。
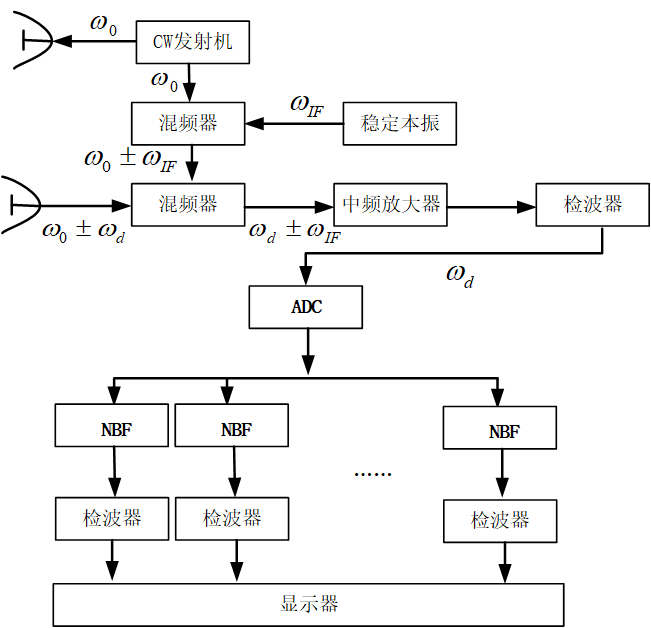
与脉冲雷达不同,连续波(CW)雷达采用连续波信号。为了保证能够连续发射能量,连续波雷达采用两部天线,一部用于发射,一部用于接收。其简化的系统框图如下图所示。图中标注了在不同位置信号频率的恰当值。
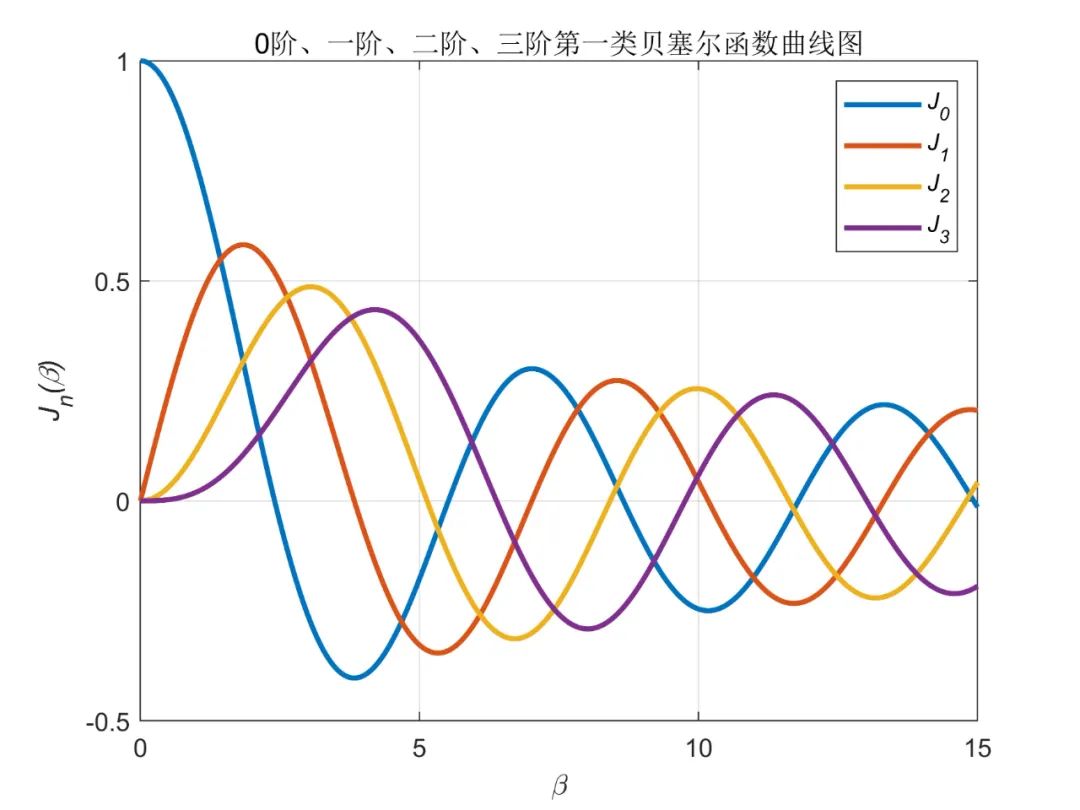
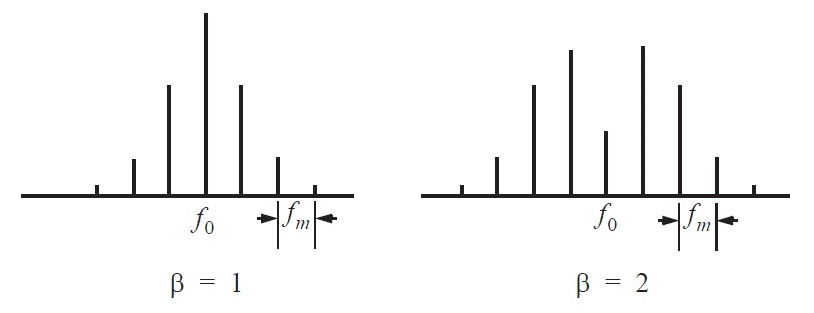
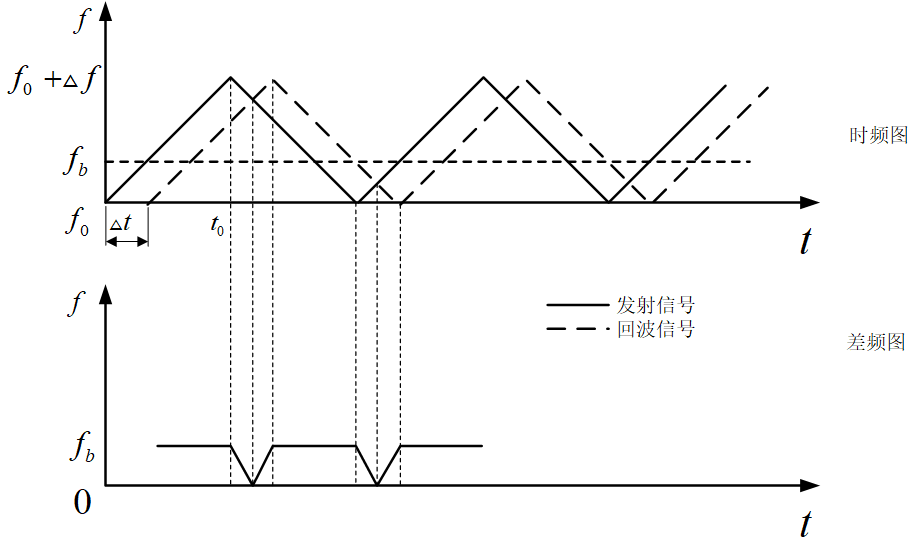
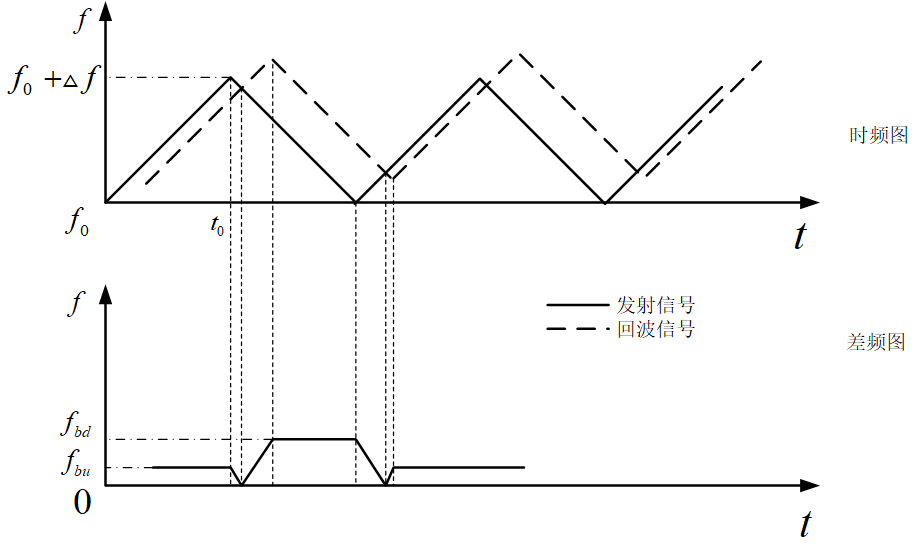
每个窄带滤波器(NBF)的带宽应尽可能的窄,这样就能精确地测量多普勒频移并使得噪声功率最小。理论上,连续波雷达的工作带宽是无限小的(因为其对应于一个无限长持续时间的连续正弦波)。然而,这样的系统物理上是无法实现的。因此,一般取连续波雷达的带宽为一个选通的连续波形的带宽。窄带滤波器组(多普勒滤波器组)是利用快速傅立叶变换(FFT)来实现的。如果多普勒滤波器组采用 点FFT来实现的,且每个滤波器带宽(FFT门)为 ,则有效的雷达多普勒带宽为 。选择因子 是因为要考虑正、负多普勒频移。将接收信号与发射信号通过鉴相器,根据相位差 可以得到目标的距离为显然,不模糊距离与 的最大值相对应。当 取最大,即 时,得到最大非模糊距离,此时不模糊距离只有半波长。因此,单频连续波雷达无法直接进行距离测量。解决的办法通常是采用线性调频技术或多载频的方案,相应的雷达称为线性调频连续波雷达或多频连续波雷达。如果特定的多普勒滤波器带宽内的输出信号值超过了检波器的检测门限,就可以检测到该滤波器带宽内的信号。由于窄带滤波器组采用FFT实现,所以每次只能处理有限长度的数据。这个长度通常称为驻留时间(Dwell time)或驻留周期(Dwell interval),用 表示,它决定了单个窄带滤波器的频率分辨率或者说带宽的大小。两者满足如下的关系式因此,窄带滤波器组的最大可分辨频率一旦被确定,其采用的傅立叶变换的点数即可按下式计算:这里的 为窄带滤波器组的最大可分辨频率。乘以系数 是因为多普勒频移有正负之分。这样就可得到下面的关系式对于连续波雷达,用驻留时间内的平均发射功率 和驻留时间 分别代替和 , , 即可得到连续波雷达方程 其中 和 分别为发射和接收天线的增益, 是与计算所用的加权窗相关的损耗因子。目标距离是通过测量目标回波的时延来计算的,由于单频连续波雷达的发射信号是连续的,因而无法直接对目标进行测距。但如果给发射和接收信号加上某种“定时标识”(Timing mark),通过比较发射信号和回波的“定时标识”,就能够测出目标回波的时延,进而测出目标的距离。“定时标识”是通过调制发射信号来实现的,一种通用的方法是线性调频(LFM)技术。采用这种技术的雷达称为线性调频连续波雷达。在具体讨论线性调频信号之前,先讨论正弦波调频信号的波形。在这里,我们只讨论正弦波形的频率调制。调频连续波(FMCW)信号可表示为式中: 为常数, 为雷达的工作频率(载频), 为调制信号, 为调制频率, 为调制带宽, 为峰值(最大)频率偏移。连续波雷达接收机利用相位检波器从回波的瞬时频率中提取目标的距离信息,如下图所示。如果能精确测出相位检波器的输出,就可精确测出时延,进而获得精确的目标距离。式中, 表示实部。由于信号 是周期性(周期为 ),因此,可将其表示为复指数傅立叶级数:作变量代换: ,不难看出 为第一类 阶贝塞尔(Bessel)函数,即这就是著名的贝塞尔—雅可比(Bessel-Jacobi)方程。下图给出了 时的第一类贝塞尔(Bessel)函数曲线。信号 的频谱是由关于 对称的成对谱线组成,下图所示为谱线分布示意图。相邻的谱线间距为 ;中央谱线的幅度为 ,而第条谱线的幅度为 。由 ,可以看出调频信号的带宽是无限大的,但高阶谱线幅度是较小的,因此可用卡森(Carson)法则将带宽近似为当 很小时,仅 和 有显著的值,FMCW信号可近似写为线性调频连续波雷达采用线性调频(LFM)连续波信号,这样既可以测量目标的距离,又可以测量目标的多普勒信息。对于实际中的连续波雷达,不可能在同一方向上持续发射线性调频信号,故而通常采用周期性调制。下图为三角型(V型)线性调频信号的时—频关系示意图。图中实线表示发射信号,虚线表示距离处的静止目标回波。 为差频,它定义为发射信号与接收信号的频率差,与目标的距离 相对应,也称位置频率(beat frequency)。 为接收信号相对于发射信号的时延。即 现在考虑存在多普勒频移(即运动目标)的情况。相应的三角型LFM信号的发射和接收波形(虚线)的示意图、对应的差频如下图所示。当目标运动时,除了由时延造成的频移外,接收信号中还包括一个多普勒频移项。分别设波形上升和下降部分的差频为 和 ,则不难得出其中为 距离的变化率,即目标相对于雷达的径向速度;上两式右端第二项即为目标的多普勒频移。由以上两式便可求出目标的距离和径向速度(距离分辨率)分别为因此,只要分别对正、负调频段的回波信号做FFT,得到目标的位置频率 和 ,就可以计算得到目标的距离和速度。为了获得好的目标距离信息,除了采用线性调频信号,连续波雷达还可采用多载频同时工作。多频方案允许连续波雷达无需利用调频就可以进行距离测量。这里讨论采用两种频率的连续波信号时的情况。若两种载频的连续波信号为其中 和 分别为目标距离相对应的时延所产生的相移。接收信号分别与两个载波进行混频、滤波、相位检波器,可得到两路回波信号的相位差为 的不模糊取值范围为 。当 时, 最大,即最大不模糊距离为因为两载频之差 ,由上式导出的值要比单一频率信号导出的值大得多,可满足实际应用的要求。
版权声明:欢迎转发本号原创内容,转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系删除。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/入群/赞助 请加微信:15881101905,备注关键词

“阅读是一种习惯,分享是一种美德,我们是一群专业、有态度的知识传播者.”
↓↓↓ 戳“阅读原文”,加入“知识星球”,发现更多精彩内容.
分享💬 点赞👍 在看❤️@以“三连”行动支持优质内容!