
来源 | 大学物理学
智库 | 云脑智库(CloudBrain-TT)
云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向
声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(15881101905,微信同号)删除,谢谢

那么,怎样才能更直观的理解散度呢?它有什么具体的物理意义呢?
诸君且听我慢慢道来。
1. 从通量说起
日常中,人们需要记录空间流过的流体的量,例如,水库泄洪的水量。但更多时候,人们需要监测流体流动的快慢,例如单位时间内,有多少流体流过去了?
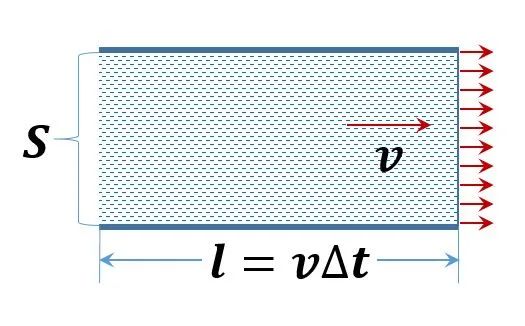
如上图所示,设水流过一个横截面积为
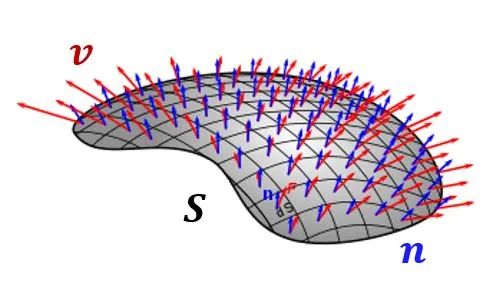
这种情况下,将曲面看作是多个细小的平面
因此,对非闭合曲面,通量可正可负,因人而异。但对闭合曲面,通量的符号是否可统一确定呢?
考虑一个球形容器,表面均匀分布无数个小孔,水从球内经小孔往外流出,同理,可得容器表面
如图,一个不断冒水和漫水的玻璃圆筒,它的侧面不透水,故通量为零;下底面有水进入,通量为负;上底面有水漫出,通量为正。

上述是用真实的流体——水来做例子说明的。但实际上,任何矢量
2. 通量的源
上面玻璃圆筒底部的有水不断冒出来,上面不断有水漫出来,你很容易想到,冒出的水时刻与漫出的水是等量的。再看下面这个灯泡,每时每刻,灯泡发出的能量,如果不考虑被空气吸收,都流过包围灯泡的某个面。

你应该知道我想说什么了,是的,流体的通量总是有源可溯的。曲面上净流出的通量总是由曲面内某种源贡献的。正电荷就是静电场的源,它像西游记中的蜘蛛精的肚脐眼一样,不断往外射出无数电场线。

如果反过来,流体不断流入曲面呢?那说明曲面内部也有一个源,不过是负的源,也称作汇,乃汇聚之意。它像一个漏洞一样,不断吸入从曲面外进入的流体。

下面动画中,瀑布的水不断注入下方的深潭,深潭是瀑布的汇,因为包围深潭的曲面的通量为负。类似的,静电场的汇就是负电荷,它看起来好像不断将电场线从外面拉进去销毁掉。

可见,这里的“汇源”可不是什么“汇聚五洲英才,源通四海财富”之意哦。
流体的源并不是只有一个点,而是分布在曲面包围的空间中,如下图中,无数迸发的火药就是出射的烟花流体的源。

显而易见,源的强弱决定了通量的大小。打个比方,有炸药发生了爆炸,形成向外扩散的气流,气流被推动的快慢取决于爆炸的威力,也就是炸药的量。它的量越大,它的冲击力导致空气朝四面八方流出的量越大。很显然,他们(空气流量与炸药量)之间就是一种通量与源的关系。

那么这个源能否量化的表示?当然!从朴素的因果关系看,闭合曲面上每时刻的通量都来自内部空间的源的贡献,如果对通量做时间积分,即从通量开始到结束的全过程求和,那得到的应该就是源的贡献总量。
例如上面那个灯泡,从它开启到关闭,所有穿过玻璃罩的光和热,也就是通量的时间积分,数量上就是光和热的源,它就是灯泡的用电量。
按此理解,若通量稳定不变,闭合曲面内部的源在任一时刻的总的贡献就是该曲面任意时刻的通量。
但若通量随时间变化,则任一时刻曲面的通量,并非其内部的源在此刻的贡献量。因为从内部各点发出的贡献抵达闭合曲面需要时间,所以通量的计算在时间上是滞后的。例如,太阳表面每时刻的辐射,来自那些同时到达太阳表面,但发生于不同时刻和不同地点的热核反应的贡献之和。
顺便说一下,在电磁学里,由于电荷分布或电流分布的变化,必须经过一段时间之后,才能够将其影响传播到场位置,产生对应的电磁作用,一般用所谓推迟势来描述。

好了,你大概明白了,通量是由曲面内部所有的点集体贡献的,这种基于点的贡献就是通量的源。关于“源”的本质,在后面第6节讲完关于通量的一个有趣的性质之后,你可能会更加明白一些。
3. 源的强度——散度
既然曲面
然而,空间内的源的强度并非均匀分布,所以这种求平均的做法意义不大。
更何况,根据前面所讲,由于时间的滞后性,对任一时刻内部空间的源的总贡献来说,它本身无法通过计算包围曲面的通量来获得。
能否想办法获得源在空间任一点的贡献呢?
若得到位于某点的一个无限小的闭合曲面
然而,凭直觉,当曲面
有了!参照上面提到的求平均值的做法,将
回想一下,在运动学中,瞬时速度的概念就是在平均速度的基础上通过如下极限来引入的
在数学上,这个量叫做
注意,这里有一个细节问题需要澄清一下。
有人提出,上述流体的速度场的的散度也可以说成
空间点附近单位体积内,在单位时间内,增加或减少的流体的量。
虽然在绝大多数情况下,这两种说法是一致的,因为一般流体传输量是守恒的,例如质量、能量等。但广义上说,这是不一定的。因为你无法确定某个量是否能凭空产生或消失。例如,只有我们确信了电荷守恒这一点后,才据此得到电流的连续性方程——后面回头讨论。
到此,你大概基本理解散度的含义了,它代表通量的源的强度,或者简单的说,散度是通量的体密度!在后面第6节中,当你了解到通量的一个有趣规律之后,这一点看起来更清楚。
那么,该如何得到散度的表达式呢?
4. 散度的表达式
如下图,设矢量
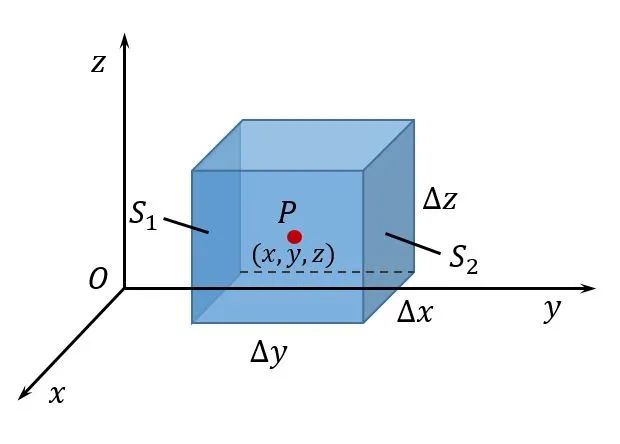
对长方体的六个面逐一计算,先考虑上图中左侧面
根据del算子的定义,上式右边为
5. 柱坐标与球坐标下的散度
先看柱坐标系的情形。
如下图,位于点P
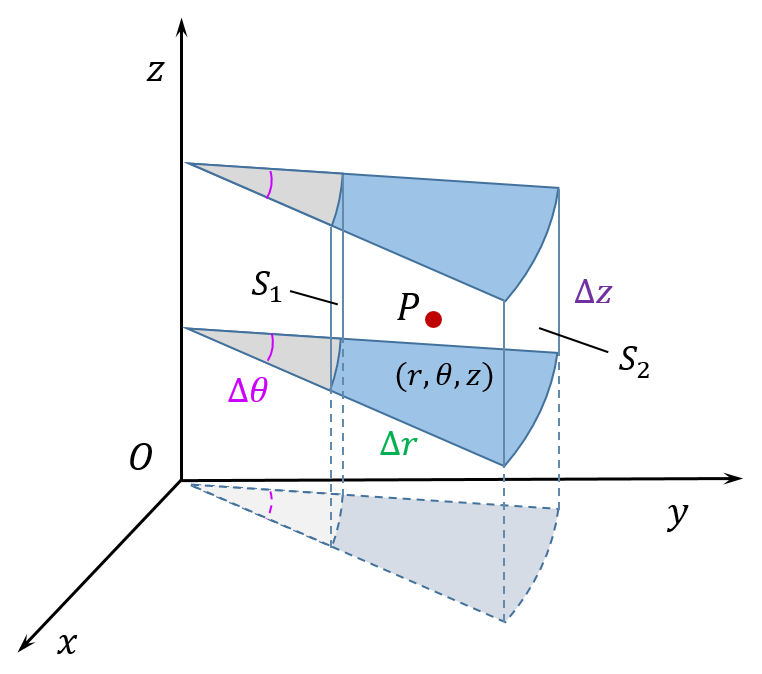
表面
故通量为
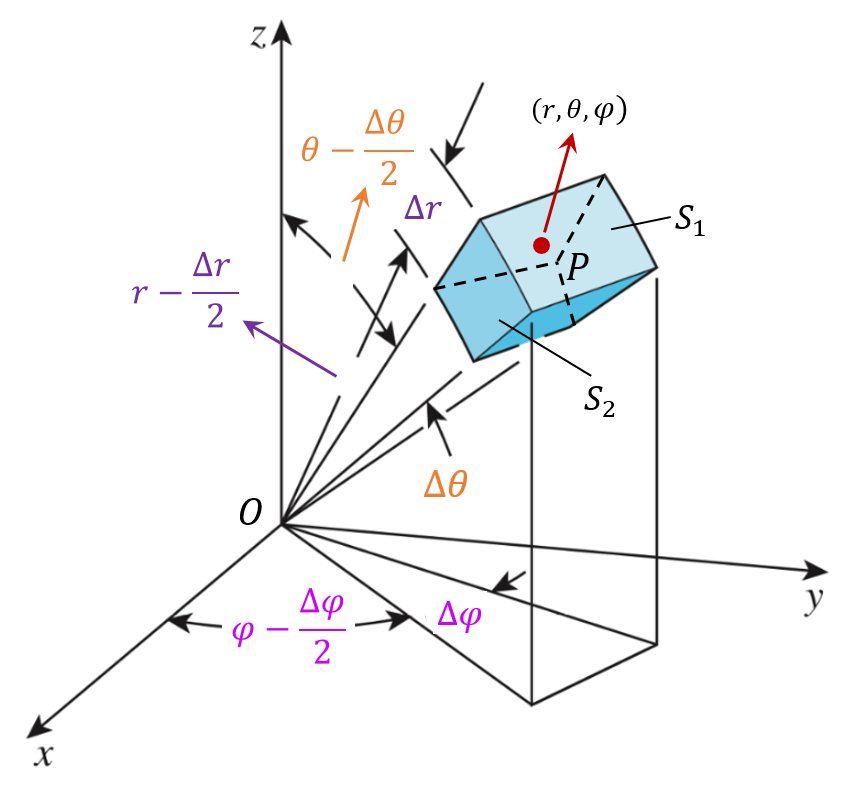
依样画葫芦,得到球坐标系中的散度表达式为
需要说明的是,上节(3)式是矢量的散度的一般表达式,任意坐标系下的表达式都服从它。
6. 高斯定理
关于散度,一个最重要的应用是,通过它,我们可将一个复杂的闭合曲面积分化为一个体积分。要理解这个问题,就要学习高斯定理。
在讲高斯定理之前,先来看通量的一个有趣的性质。
假设一个闭合曲面
下面以
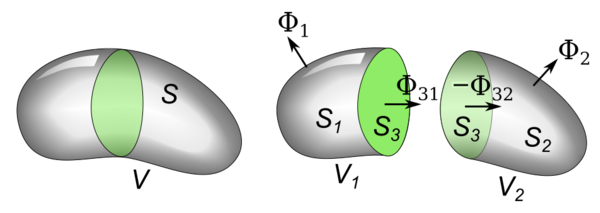
先来看两个切面
故得
因此,总通量等于两部分体积的表面的通量之和。
若将
是不是觉得通量有点像质量?
是的!只不过通量有正负之分,但实际上广义的质量也可为负。
所以,通量与散度的关系,类似于质量与密度的关系,因为质量也等于内部各个部分的质量之和,每一个部分的质量都占一部分体积,密度就是质量与体积的比,正如散度是通量与体积的比。
因此,散度的含义看起来更加清晰,它就是通量的体密度!
讲到这里,突然意识到,前面第2节“通量的源”中所说的源就是将空间分成无限小的子块时,各小块的表面积的通量。换句话说,源的本质是无限小闭合曲面的通量。源与通量的关系,类似于质点与质量的关系。
将此规律按照通量的定义写出来就是
式中
好了,现在据此推导高斯定理。将上面的关系式右边稍作变形
根据此定理,矢量场的通量可以化为它的散度的体积分。后面将举例说明它的应用。
7. 一个例子——静电场
前面提到,形成通量以及散度的矢量
静电场是静止的点电荷激发的,考虑真空情况,表达式为
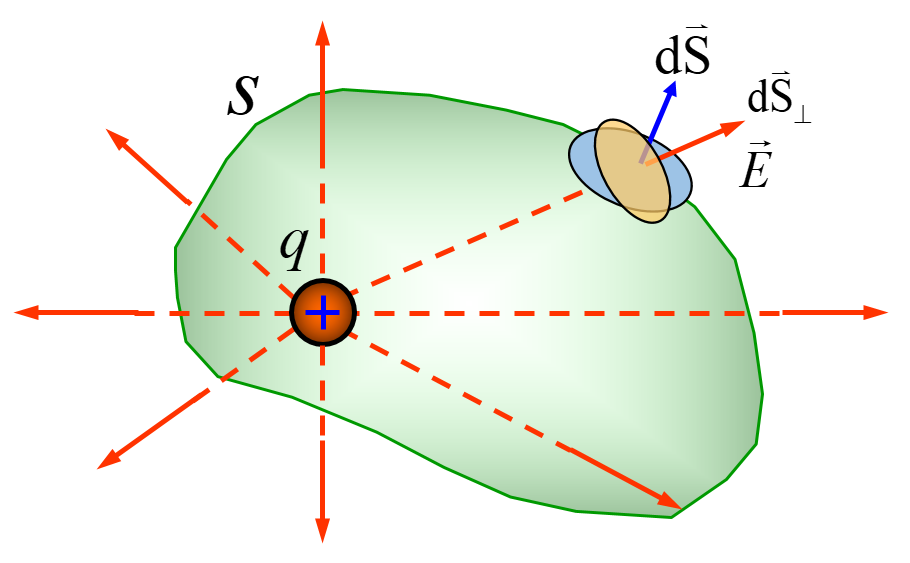
考察曲面上微元
那么,若某闭合曲面
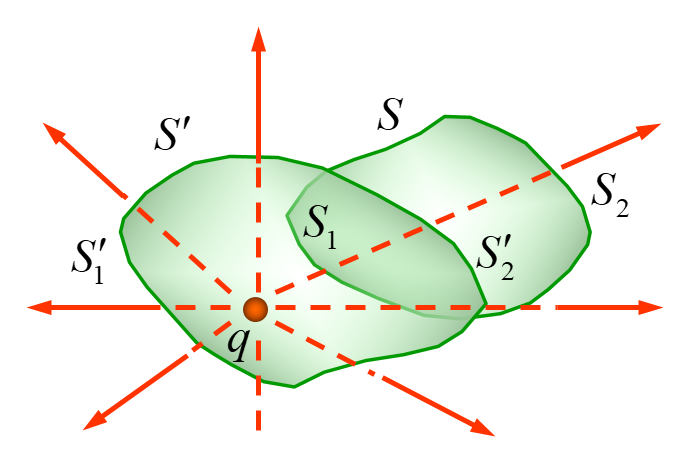
如图所示,点电荷
而
同理,
考虑到前面提到的电场强度的叠加性,现在可以得出静电场的高斯定理:任意曲面的电场通量等于所包围电荷的代数和除以
根据正负电荷的不同情况,高斯定理中的电荷或电荷密度相应的取正或负。因此,由于正电荷激发的电场指向四周,而负电荷相反。因此,对闭合曲面来说,内部正电荷的电场将从内往外穿过,而负电荷则相反。所以,正电荷为包围它的闭合曲面提供正的通量,负电荷相反。
若采用电场线来描绘电场,则可更加直观的理解上述规律。
根据法拉第的电场线的概念,既然电场可用电场线描绘,若按照一定的比例画电场线,使单位面积内条数在数量上正好等于电场强度的大小,即
也就是说,电场通量可被看作为电场线的条数。
如果某点有正电荷或负电荷,包围该点的无限小闭合曲面必有电场线流出或流入;反过来,如果某个点有电场线冒出或消失,则该点必然有正电荷或负电荷。换句话说,电场线不会在没有电荷的地方中断。
这样,我们就很容易理解这样一个事实:层层包裹着电荷的不同曲面必定具有相等的电场通量。虽然前面已经证明了这个结论。
可以想象,当你站在曲面外看时,正电荷的电场线就从曲面射出,而负电荷的电场线则从外面吸入。基于这样一种物理图像,我们将正电荷称作电场的源,而将负电荷称作电场的汇。
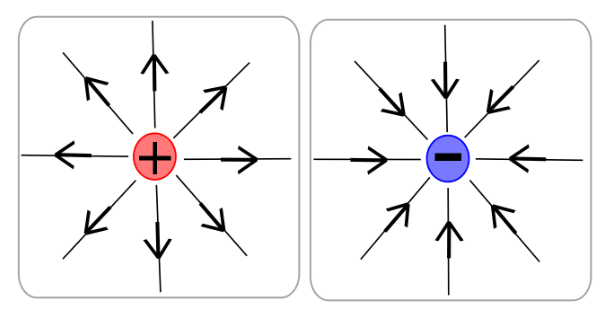
当然,如果从激发电场的角度来说,无论正负电荷,都是电场的源。
8. 另一个例子——电流的连续性方程
上面讲了真空的静电场的散度,它对应的量是电荷的空间密度
现考察电流密度
电流密度是电荷流体的速度场矢量,即
根据散度定理有
如果电荷不能被创造,也不能被消灭,即电荷是守恒的,那么除了电荷转移之外,没有其他改变电荷量的途径。因此,单位时间内,穿过曲面流出的电荷量与内部空间电荷的减少量必定相等,即
如果每个地方的电荷都不随时间变化,即上式右边为零,那么得
9. 散度的物理意义
从散度的表达式——(2)式或更一般的(3)式来看,散度乃场矢量的分量的偏导之和,但这到底代表什么意思呢?
有人说,这代表了场矢量随空间坐标的变化率。但这种仅从数学式表面的理解并无多大帮助,并且极易与梯度混淆,而导致理解错误。
例如,点电荷的电场既然随坐标变化,从直观上看,在任一点的偏导好像不应该为零,因此应该有散度?是这样吗?
数学计算最可靠,咱们来算一下就知道了。
因为点电荷的电场分布具有球对称性,用球坐标更方便,表达式为
其实这也难怪,散度的表达式只是严格计算的数学方法,它才不需要直观呢!
那么,我们就从别的角度来看散度的意义吧。
第一个角度,散度的定义式,即(1)式
这里的极限表示曲面无限缩小到那个点,也即是从那个点有场产生,换句话说,如果散度不为零,就意味着那个点成为场的源头,它激发了场,而这个场因为具有源,而称为有源场。
例如太阳内部,凡是热核反应的点,散度不为零,就是辐射源。水池底部,凡是冒水或漏水的孔眼,散度都不为零,就是水的源。
对真实的流体的速度场
第二个角度,散度定理,即(4)式
简单的说,散度就是某种物质的密度。
当然,物质实际上往往并不存在,但我们仍然可以想象有一种物质,例如对电场电场来说,根据上一节静电场部分所讲,这种物质就是电荷——虽然电荷并非真正的物质。
对静电场来说,(4)式具体化为(5)式或(6)式,电场背后的这种物质就是电荷,而电荷的密度
那么,什么情况下,散度成为真实物质的密度呢?
答案是万有引力场。
考虑质点
再回到散度定理。闭合曲面的通量由曲面内部空间中的某种“物质密度”——散度的体积分决定,即使外部也存在这种“物质密度”,不会对曲面通量产生贡献。换句话说,曲面的通量源于内部的源的贡献,与不属于曲面内的源无关。
如果把场线看作是流体速度场,你站在一个闭合曲面外面,从哪个曲面冒出流体,你自然认为这些流体都源于哪个曲面中的一些流体源;如果有流体进入这个曲面,你也会认为曲面内包含了一个流体源,不过它是负源,或者称作汇。

多年前某个冬日的下午,我忍着饥饿听高数老师讲高斯定理。好不容易熬到下课,饥肠辘辘的我冲进食堂,一个个可爱的肉包子映入我的眼帘。显然我强烈的感受到这种不断从包子内散发出的诱惑力,而它们那顶部呈现辐射状花纹更加暗示了它们的含肉量极大——散度!
我顿悟了。
从一颗香喷喷的包子里发出的诱惑力由包子里的肉量来决定,与包子外面的肉量无关。
10. 拉普拉斯算子
散度是哈密顿算子与矢量点积,如果这个矢量是某个标量的梯度,那么就导致了梯度的散度,在直角坐标系中就是
如果空间只有一维,Laplacian退化为二阶导数。也就是说,一元函数的二阶导数可看作是Laplacian的一个特例,这有助于理解Laplacian的意义。
对一元函数
而对二元函数
而对凹点或凸点,Laplacian取正或负,它源于场函数的梯度的散度为正或负。如下图所示,凹点附近,场线为向外射出的箭头——源;凸点附近,场线为向内射入的箭头——汇。
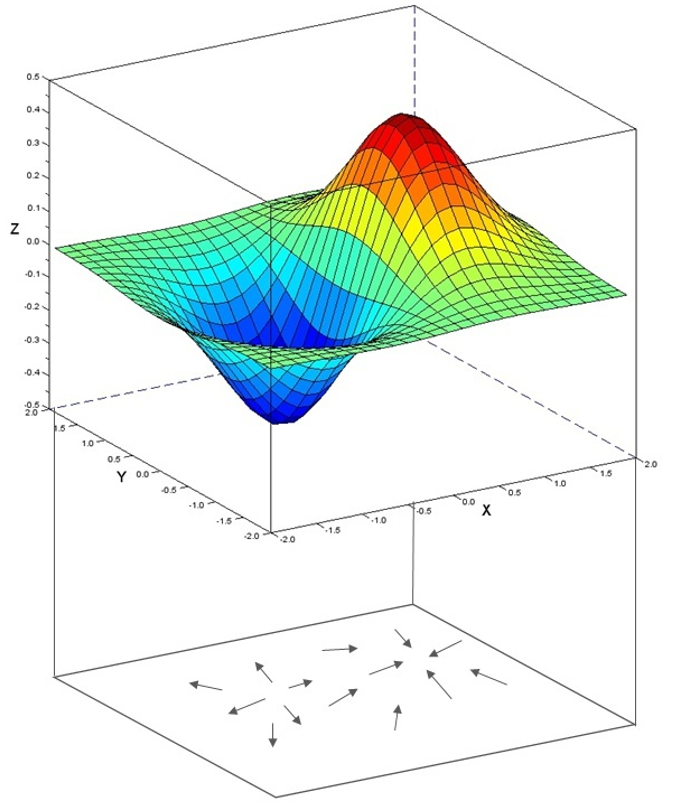
就拿电场来说把,若某点电势满足
同样对电场来说,根据
为了看清Laplacian的意义,下面我们来看一个点从凹点移到凸点过程中Laplacian变化。
当它位于凹点时,周围都比它高,它的Laplacian大于零;随着这个点移向凸点,周围出现比它还低的点,但比它高的点还占多数,这导致它的Laplacian减小;直到抵达某个平坦位置——确切的说是坡度恒定的位置,这个点周围比它低的点与比它高的点一样多,它的Laplacian变为零;然后逐渐的,它周围比它低的点逐渐占上风,Laplacian小于零;直到当它出现在凸点处时,周围所有点都比它低,Laplacian取负值。
可见,Laplacian可直观的被理解为场的平均变化率,即曲面上某点与附近各点连线的斜率的平均值。
当场函数往下凹时,则场的平均变化率为正,反之为负。对那些均匀变化的场,它将描绘一个平面——不是水平面,场函数的平均变化率为零。而若场在某点的平均变化率为零,则场在该点的值可用附近各点的平均值来代替。
Laplacian是图像处理领域重要的数学工具之一。
例如,它常被用来检测图像边缘。其基本原理是,当图像平滑的变化时,Laplacian接近0;而当图像强度明显变化的区域,Laplacian的绝对值较大。
再例如,它还被用于增强图像,调整图像亮度和颜色的过渡等。
拉普拉斯算子的应用非常广泛,但篇幅有限,就不再过多涉及了。
- The End -
版权声明:欢迎转发本号原创内容,转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系删除。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/入群/赞助 请加微信:15881101905,备注关键词

“阅读是一种习惯,分享是一种美德,我们是一群专业、有态度的知识传播者
↓↓↓ 戳“阅读原文”,加入“知识星球”,发现更多精彩内容.
分享💬 点赞👍 在看❤️@以“三连”行动支持优质内容!