史密斯圆图对于射频设计的重要性不言而喻,在软件如此发达的今天,我们直接在圆图工具软件上直接画圈圈就可以轻松搞定匹配。但是我们学习的目的:不仅仅是知其然,更重要的是知其所以然。这也是RF小木匠不断的写作的原因,知其然,而后知其所以然,最后排文输出,让更多的同学知其所以然。
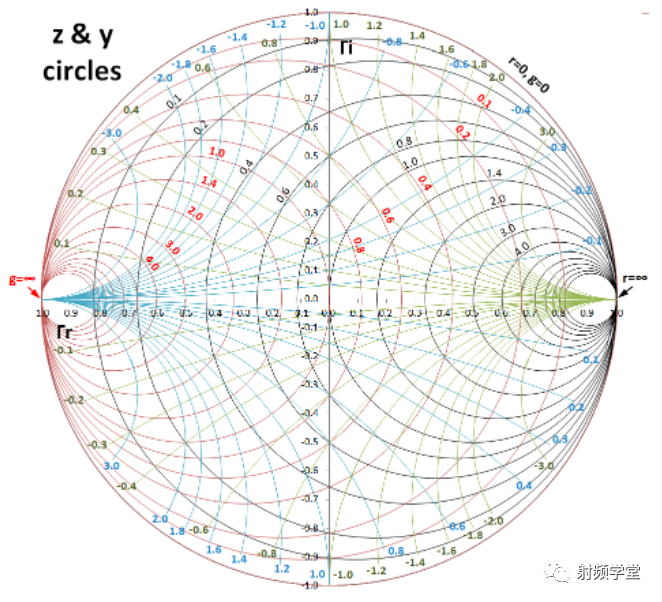
史密斯圆图主要解决了传输线理论中的阻抗匹配问题,提到传输线理论,那必然涉及到传输线的几个重要参数:Z参数,Y参数,分布式阻抗R,G,X,反射系数┏,和驻波比VSWR。无外乎,史密斯圆图就是来描述传输线的这些参数的。
阻抗匹配的目的就是让负载接受最大的功率传输,这个时候源阻抗和负载阻抗必须共轭匹配。
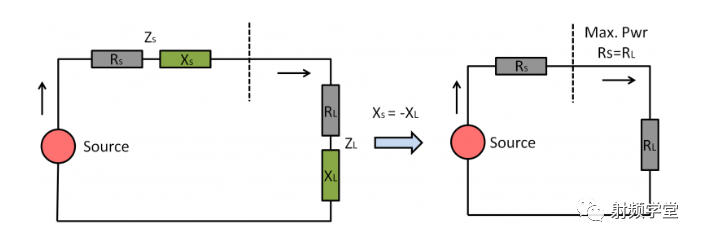
共轭匹配是个什么玩意呢?
比如说源阻抗和负载阻抗分别是:

那么共轭匹配就是要求:
也就是说,电阻要相等,电抗等额反相。
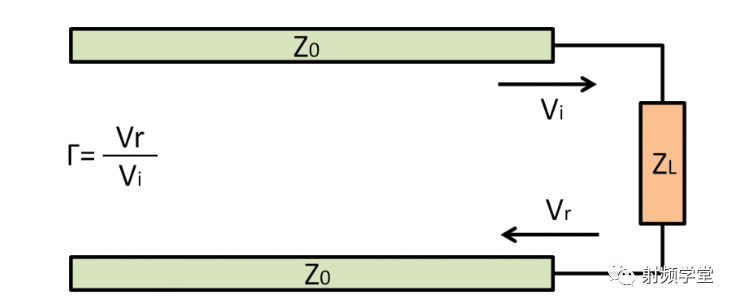
但是绝对的相等很难达到的,我们就需要找到一个描述源阻抗和负载阻抗关系的参数,这个参数就叫做反射系数┏,就是反射电压和入射电压的比值,如下图所示。
展开就是:
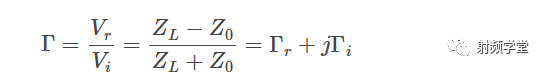
为了让上式更具有一般性,我们引入了归一化阻抗 z 这个概念,归一化就是无论Z0是多少,我们让所有阻抗对Z0归一即可。这个在史密斯圆图中很有用,其实在射频设计中也很有用,虽然我们通常面对的归一化Z0是50欧姆,但是如果换成其他阻抗,归一化阻抗的价值就体现出来了。
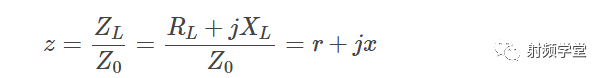
这样,反射系数就可以表示为
图示如下。
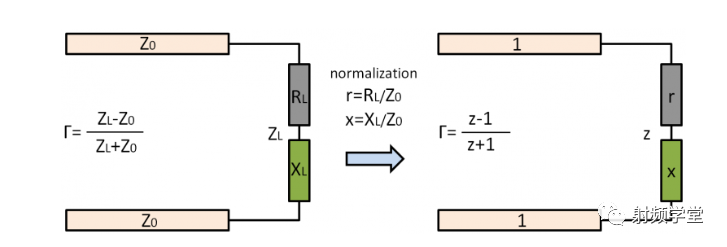
到这,史密斯圆图的第一步就要开始了。
我们对反射系数的实部和虚部分别进行计算。
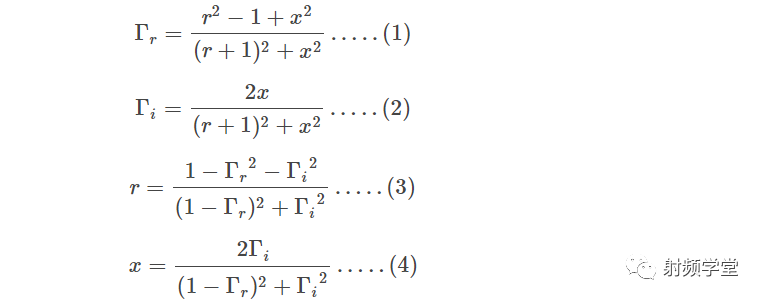
我们就得到了反射系数分别关于r和x的圆方程,如下所示。
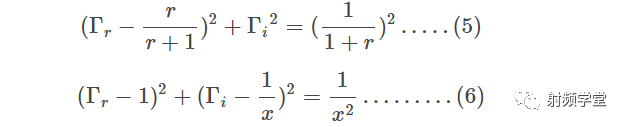
这样史密斯圆图中的两个最基本的电阻r圆和电抗x圆就出来了,如下图
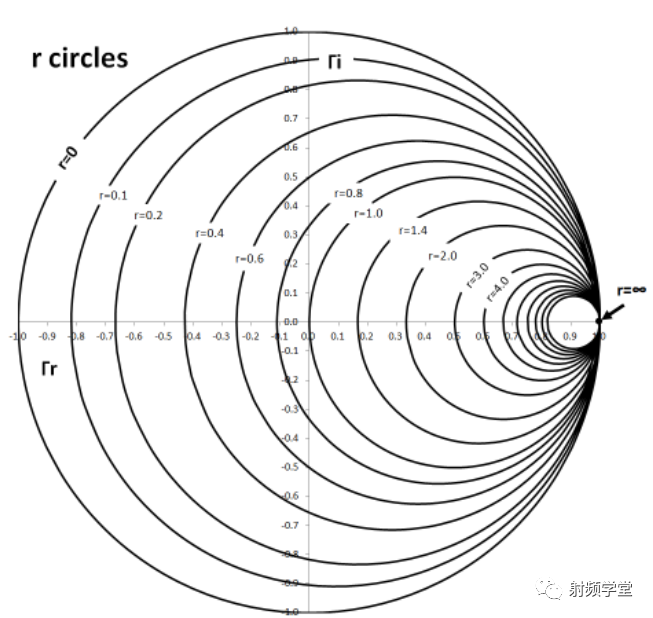

同样的,对于有些电路,我们更喜欢用导纳参数Y来表示,比如并联电路。根据导纳参数Y和阻抗参数Z的倒数关系,
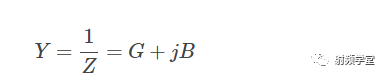
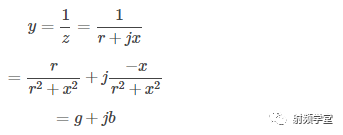
我们得到另外两个圆:电导g圆和电纳b圆

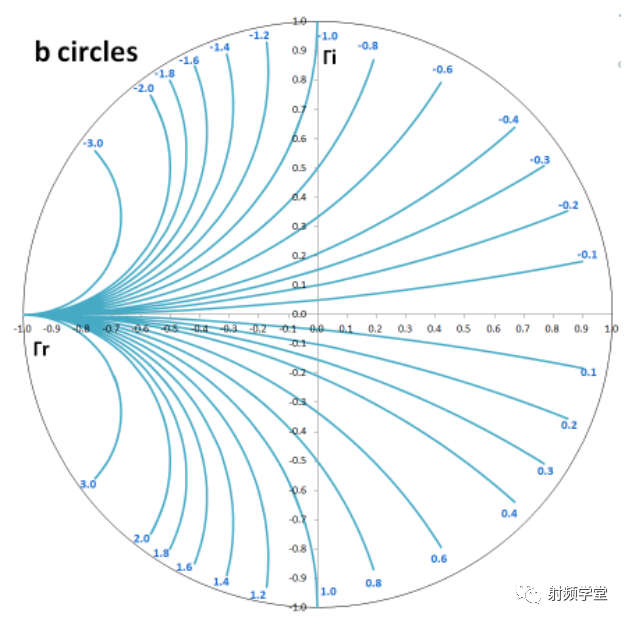
把这四个圆叠加到一幅图上,一个基本的史密斯圆图就完成了,看上去很复杂,其实分解开,也就这四个圆。不得不佩服史密斯大神的智慧,在当时计算机还不普及的情况下,如果没有圆图,像完成阻抗匹配真是难于蜀道。