从时域到频域
这里以快速傅里叶变换(FFT)为对象举实例进行解释,并附上全部MATLAB代码。
另外,说明一下,用MATLAB做FFT并不要求数据点个数必须为以2为基数的整数次方。之所以很多资料上说控制数据点数为以2为基数的整数次方,是因为这样就能采用以2为基的FFT算法,提升运算性能。
如果数据点数不是以2为基数的整数次方,处理方法有两种,一种是在原始数据开头或末尾补零,即将数据补到以2为基数的整数次方,这是“补零”的一个用处;第二种是采用以任意数为基数的FFT算法。
而MATLAB的 fft(x,N) 函数在参数 N 正好就是数据 x 的长度,但又不是以2为基数的整数次方时,并不会采用补零的方法,而应该是采用以任意数为基数的FFT算法(说“应该”是因为帮助文档里没有明确说明),这样也能得到很好的结果,只不过速度要稍稍慢了一些,以通常的计算量是体现不出来的。
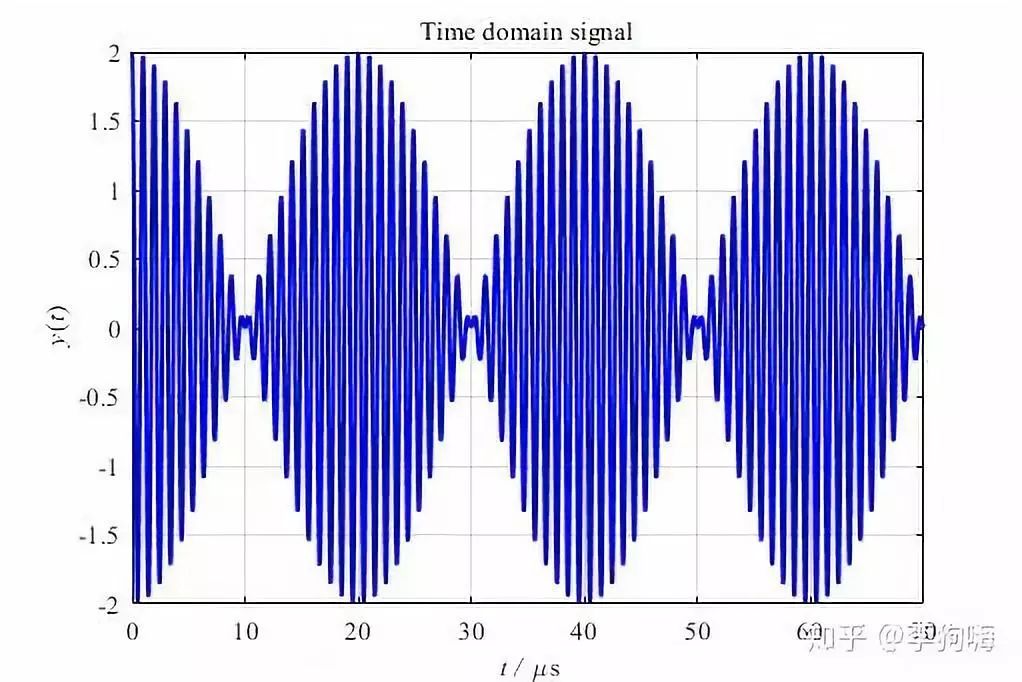
比如,现在有一个信号,这个信号中仅包含两个正(余)弦波,一个是 1 MHz ,一个是 1.05 MHz ,即 x = cos(2π×1000000 t) + cos(2π×1050000 t) 。设定采样频率为 Fs=100 MHz,如果采 1000 个点,那么时域信号的时长就有 10 μs。

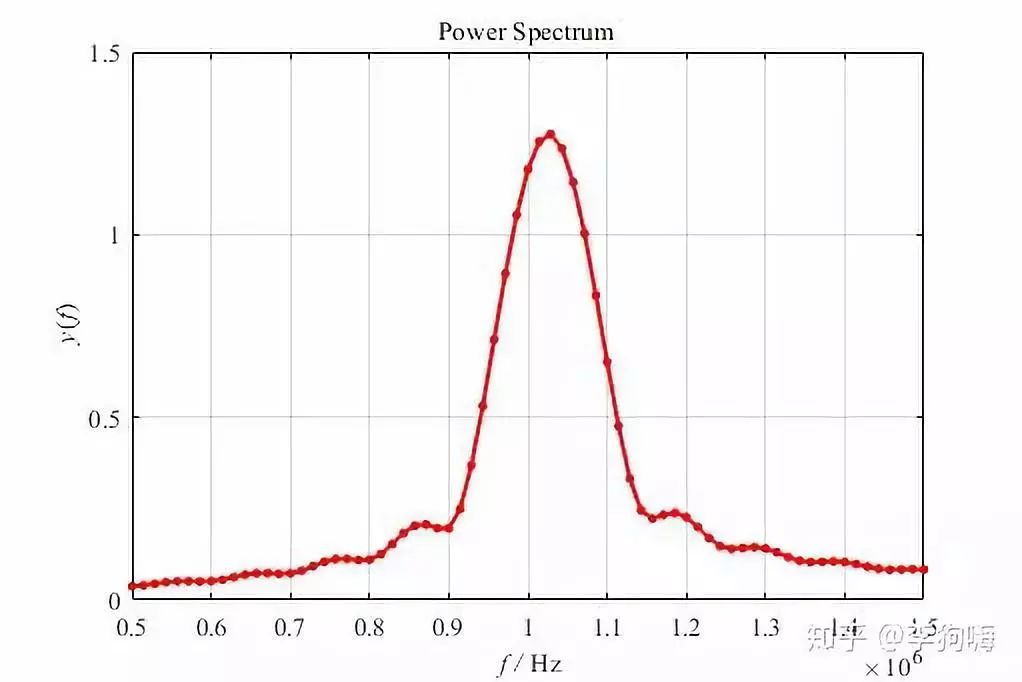
如果,直接对这1000个数据点做快速傅里叶变换,将得到频谱图:

可以发现,频谱点稀疏,在1MHz附近根本无法将1 MHz 和1.05 MHz 的两个频率分开。
clear;clcclose all%% FFTFs = 100e6; % Sampling frequency / HzT = 1/Fs; % Sampling time / sL0 = 1000; % Original signal lengthL = 1000; % Data lengtht0 = (0:L0-1)*T; % Original signal time sequencex = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % Signal functiont = (0:L-1)*T; % Data time sequence%% Plotfigure(1)plot(t*1e6,x,'b-','linewidth',1.5)title ('\fontsize{10}\fontname{Times New Roman}Time domain signal')xlabel('\fontsize{10}\fontname{Times New Roman}\it t /\rm \mus')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itt\rm)')grid on;axis([0 10 -2 2])set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')%% FFTY = fft(x); % FFT% Calculate double sides spectrum P2, and then calculate single side% spectrum P1 based on P2 and even data lengthP2 = abs(Y/L0);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = Fs*(0:(L/2))/L;% Rfftfigure(2)plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)axis([0.5e6 1.5e6 0 1.5])title('\fontsize{10}\fontname{Times New Roman}Power Spectrum')xlabel('\fontsize{10}\fontname{Times New Roman}\it f /\rm Hz')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itf\rm)')grid on;set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
发现频率成分无法被区分开来,第一反应应该就是:频率分辨率不够。那么,如何提高频率分辨率呢?首先要清楚,这里存在两种类型的频率分辨率。
一种叫波形分辨率,其由原始数据的时间长度决定:
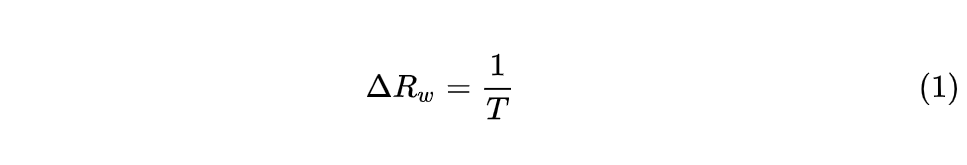
另一种可以称之为视觉分辨率或FFT分辨率,其由采样频率和参与FFT的数据点数决定[1]:

之所以要区分,就是因为后面要进行“补零”的操作。如果不补零,直接对原始数据做FFT,那么这两种分辨率是相等的。
例如上面,有:
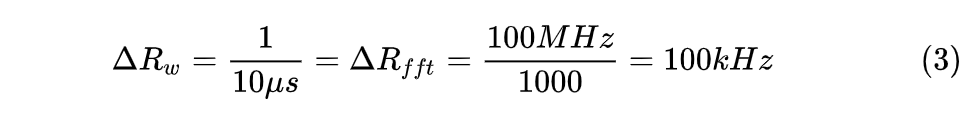
那么,如果现在在原始数据点后补零会有什么效果呢?假设在这 1000 个原始数据点后面再补充零达到 6000 个点,那么数据变成了:

此时对其做快速傅里叶变换,结果如下:
可以发现,频谱点密集了不少,但是在 1MHz 附近依然无法将 1MHz 和 1.05MHz 的两个频率成分分开。这是因为从式 (1) 可以看出,波形分辨率只与原始数据的时长 T 有关,而与参与FFT的数据点数无关。虽然补了很多零,但波形分辨率依然为1/10μs= 100 kHz,该分辨率大于1MHz 和 1.05MHz 这两个频率成分之间的距离50 kHz 。这就好比用筛子分黄豆和大米,分辨率就好像是筛子上孔的大小,如果筛子的孔太大了,就没有办法把这两者分开。
而“时域补零相当于频域插值”[2],也就是说,补零操作增加了频域的插值点数,让频域曲线看起来更加光滑,也就是增加了FFT频率分辨率,注意式(2) 所示,这是“补零”的另一个原因。
clear;clcclose all%% FFTFs = 100e6; % Sampling frequency / HzT = 1/Fs; % Sampling time / sL0 = 1000; % Original signal lengthL = 7000; % Data lengtht0 = (0:L0-1)*T; % Original signal time sequencex = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % Signal functiont = (0:L-1)*T; % Data time sequencey = zeros(1,L);y(1:L0) = x;%% Plotfigure(1)plot(t*1e6,y,'b-','linewidth',1.5)title('\fontsize{10}\fontname{Times New Roman}Time domain signal with Zero Padding')xlabel('\fontsize{10}\fontname{Times New Roman}\it t /\rm \mus')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itt\rm)')grid on;axis([0 70 -2 2])set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')%% FFTY = fft(y); % FFT% Calculate double sides spectrum P2, and then calculate single side% spectrum P1 based on P2 and even data lengthP2 = abs(Y/L0);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = Fs*(0:(L/2))/L;% Rfftfigure(2)plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)axis([0.5e6 1.5e6 0 1.5])title('\fontsize{10}\fontname{Times New Roman}Power Spectrum')xlabel('\fontsize{10}\fontname{Times New Roman}\it f /\rm Hz')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itf\rm)')grid on;set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
显然,根据上面的分析可知,在采样频率不变的情况下,要想将 1MHz 和 1.05MHz 这两个频率成分分析出来,光靠“补零”是不够的,必须要改变波形分辨率,也就是要延长原始数据的时长。现在以相同的采样频率对信号采 7000个点作为原始信号:
对其做快速傅里叶变换,结果如下:
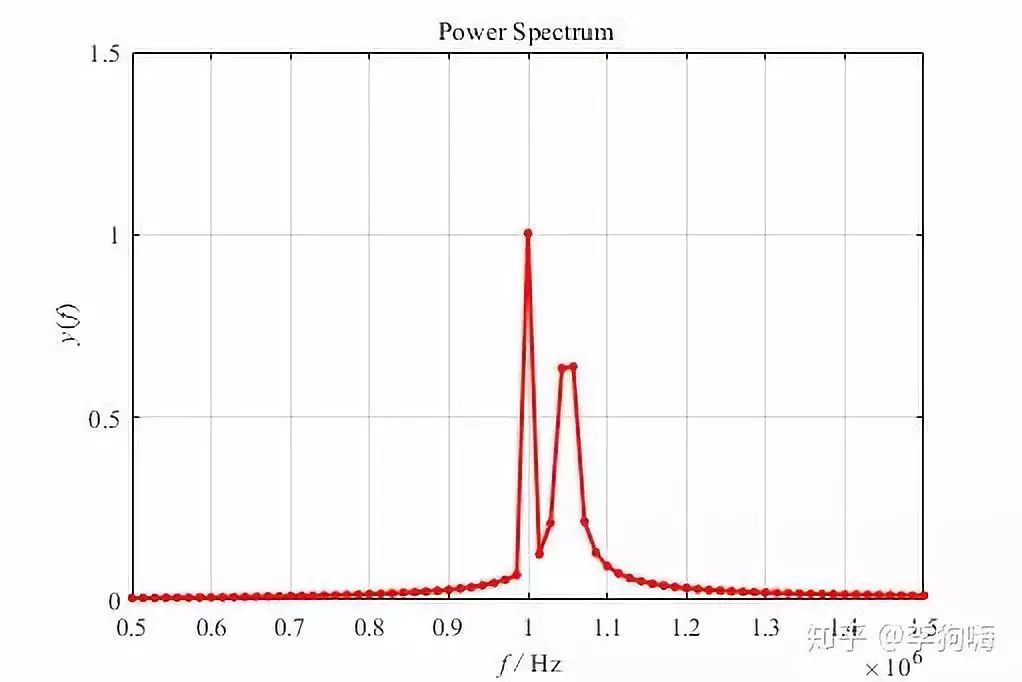
因为此时的波形分辨率为:1/70μs≈14kHz ,小于 1MHz 和 1.05MHz 这两个频率成分之间的距离 50 kHz ,所以可以看出有两个明显的峰值。
但是会发现 1MHz 对应的幅值为1,与原始信号中该频率成分的幅值一致,但 1.05MHz 对应的幅值明显低于1,但是其周边的点上却都有不小的幅值,这就是所谓的频谱泄露,因为数据点的个数影响,使得在 1MHz 处有谱线存在,但在 1.05MHz 处没有谱线存在,使测量结果偏离实际值 ,同时在实际频率点的能量分散到两侧的其它频率点上,并出现一些幅值较小的假谱。
clear;clcclose all%% FFTFs = 100e6; % Sampling frequency / HzT = 1/Fs; % Sampling time / sL0 = 7000; % Original signal lengthL = 7000; % Data lengtht0 = (0:L0-1)*T; % Original signal time sequencex = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % Signal functiont = (0:L-1)*T; % Data time sequence%% Plotfigure(1)plot(t*1e6,x,'b-','linewidth',1.5)title('\fontsize{10}\fontname{Times New Roman}Time domain signal')xlabel('\fontsize{10}\fontname{Times New Roman}\it t /\rm \mus')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itt\rm)')grid on;axis([0 70 -2 2])set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')%% FFTY = fft(x); % FFT% Calculate double sides spectrum P2, and then calculate single side% spectrum P1 based on P2 and even data lengthP2 = abs(Y/L0);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = Fs/2*linspace(0,1,L/2+1);% Rfftfigure(2)plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)axis([0.5e6 1.5e6 0 1.5])title('\fontsize{10}\fontname{Times New Roman}Power Spectrum')xlabel('\fontsize{10}\fontname{Times New Roman}\it f /\rm Hz')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itf\rm)')grid on;set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
为了解决这个问题,可以设法使得谱线同时经过1MHz 和 1.05MHz 这两个频率点,找到他们的公约数。
如果原始数据不变,在后面再补充 1000 个零点:
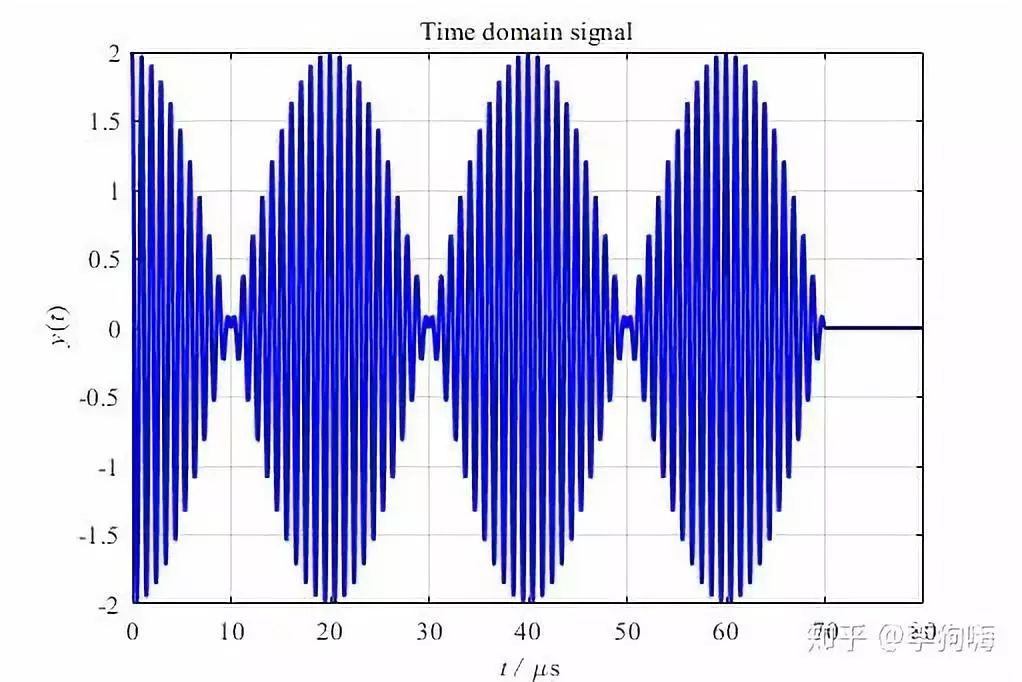
那么FFT分辨率就是 12.5kHz ,是这两个频率的公约数, 1MHz=80×12.5kHz ;1.05MHz=84×12.5kHz ,所以谱线同时经过 1MHz 和 1.05MHz 这两个频率点。
对其做快速傅里叶变换,结果如下:
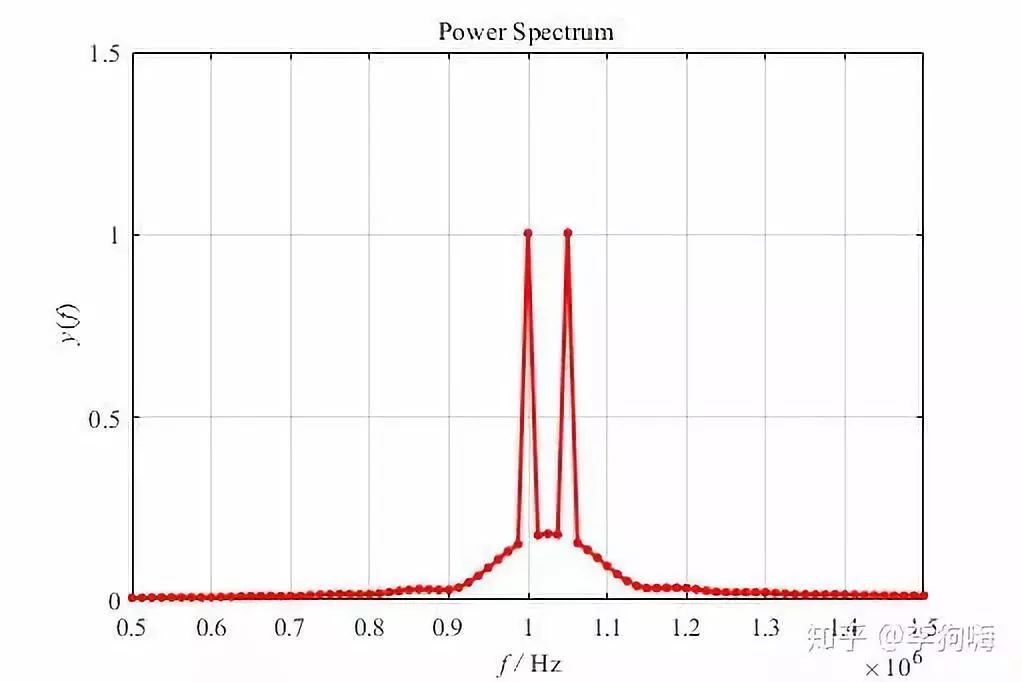
会发现 1MHz 和 1.05MHz 对应的幅值均为1,与原始信号一致。这也是一种补零操作带来的影响。
clear;clcclose all%% FFTFs = 100e6; % Sampling frequency / HzT = 1/Fs; % Sampling time / sL0 = 7000; % Original signal lengthL = 8000; % Data lengtht0 = (0:L0-1)*T; % Original signal time sequencex = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % Signal functiont = (0:L-1)*T; % Data time sequencey = zeros(1,L);y(1:L0) = x;%% Plotfigure(1)plot(t*1e6,y,'b-','linewidth',1.5)title('\fontsize{10}\fontname{Times New Roman}Time domain signal')xlabel('\fontsize{10}\fontname{Times New Roman}\it t /\rm \mus')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itt\rm)')grid on;axis([0 80 -2 2])set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')%% FFTY = fft(y); % FFT% Calculate double sides spectrum P2, and then calculate single side% spectrum P1 based on P2 and even data lengthP2 = abs(Y/L0);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = Fs/2*linspace(0,1,L/2+1);% Rfftfigure(2)plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)axis([0.5e6 1.5e6 0 1.5])title('\fontsize{10}\fontname{Times New Roman}Power Spectrum')xlabel('\fontsize{10}\fontname{Times New Roman}\it f /\rm Hz')ylabel('\fontsize{10}\fontname{Times New Roman}\it y\rm(\itf\rm)')grid on;set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
图8 中会有一些旁瓣出现,这是因为补零影响了原始信号,如果,直接采8000个点作为原始数据,即将程序中的L0改为8000,那么有:
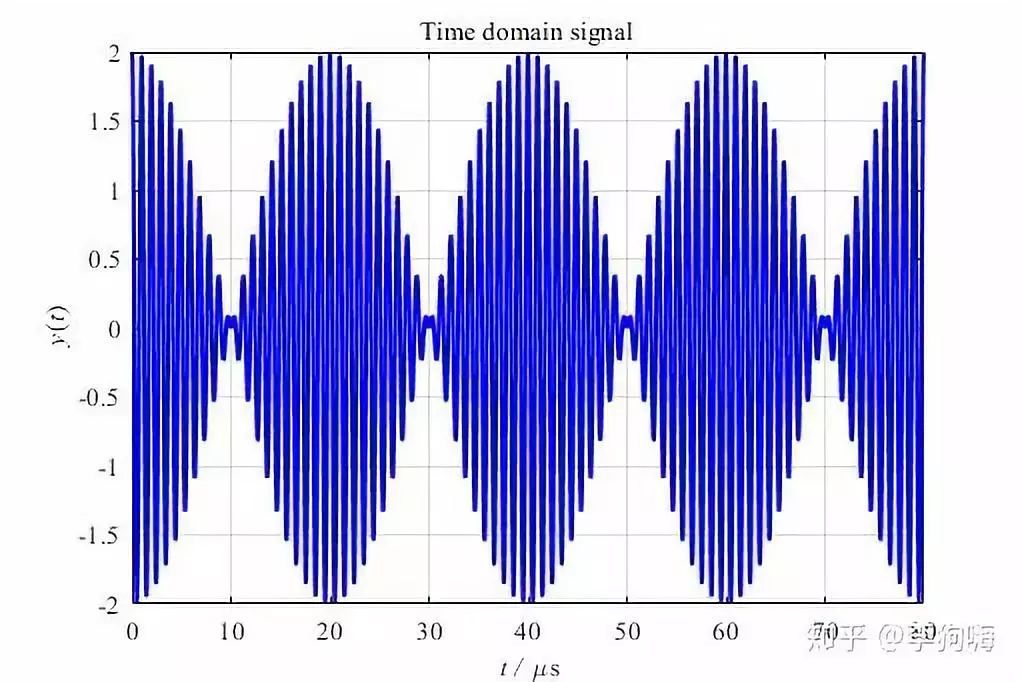
并对其做FFT,结果如下

这样也就不存在补零带来的误差了。
Zero Padding http://www.bitweenie.com/listings/fft-zero-padding/
ZeroPaddingTheorem https://ccrma.stanford.edu/~jos/dft/Zero_Padding_Theorem_Spectral.html