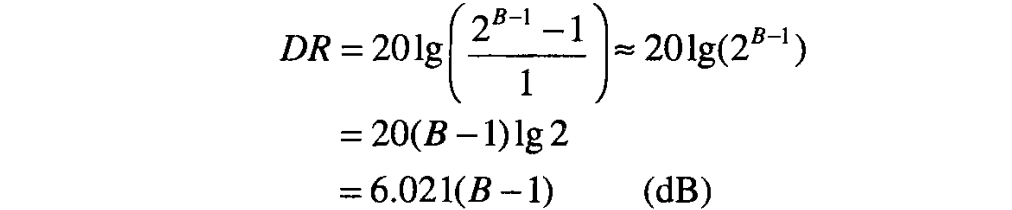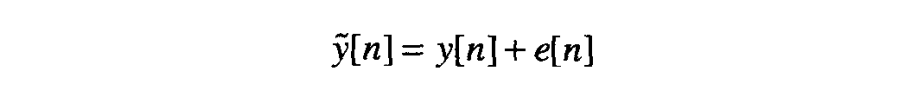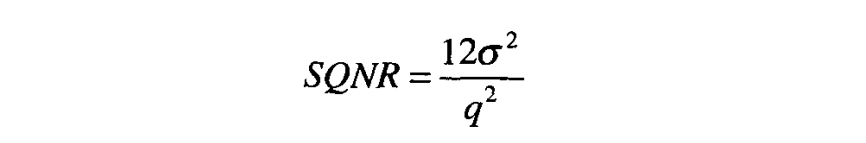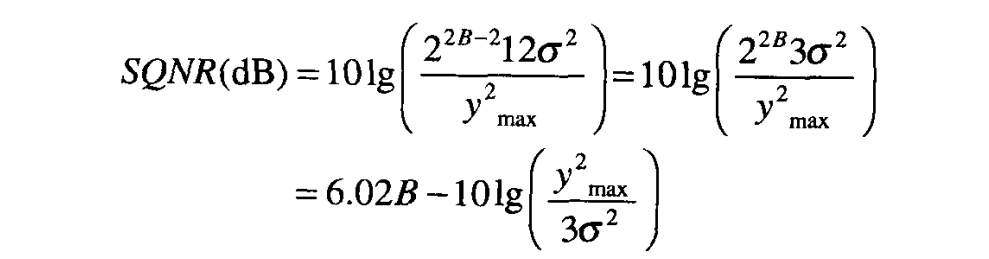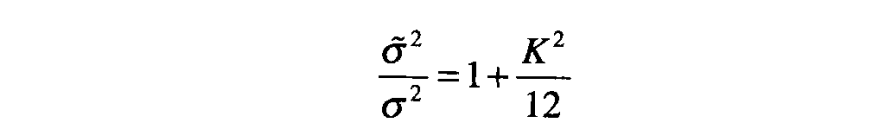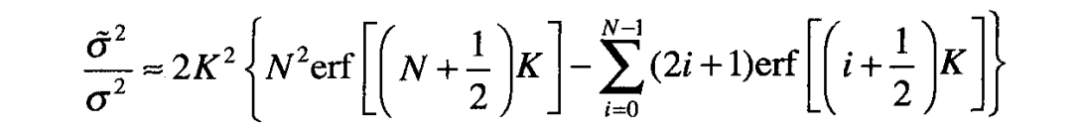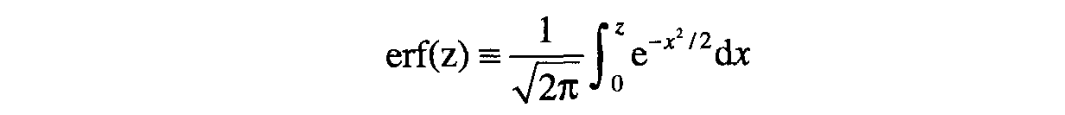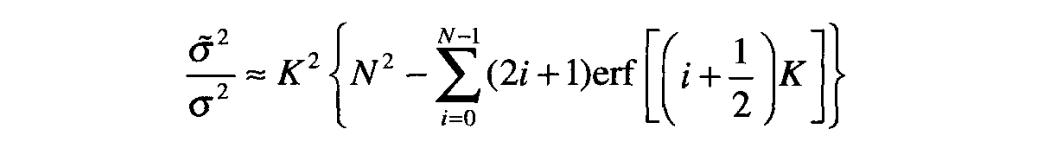来源 | 雷达信号处理matlab

智库 | 云脑智库(CloudBrain-TT)

云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向

声明 | 本号聚焦相关知识分享，内容观点不代表本号立场，可追溯内容均注明来源，若存在版权等问题，请联系(15881101905，微信同号)删除，谢谢

将模拟信号转化成数字信号需要进行两个操作。首先就是采样，这是前面所讨论。但是，对于离散域（例如，离散时间域）信号的每个样本  ，其幅度仍是连续的，因此必须被量化，也就是将其转换为一个仅取有限数量幅度的量化值  。本期将讨论由数字信号量化所产生的影响。

假设采用  位字节表示每个信号样本，则可能的数字表示有  个。但是，实际可被编码的不同峰值数取决于所采用表示方案的个数，两种通常的做法是取二进制补码及带符号的幅度编码。

二进制补码可以在  区间内容纳  个不同峰值。注意，该范围是不对称的。带符号的幅度编码在对称区间  内容纳  个不同峰值。在这种方法中，可表示的峰值数比第一种方法少一个，因为它同时对  和  进行了编码；而在第一种方法中，对于零的编码是唯一的。

  位量化器的可支持最大动态范围（dynamicrange，DR）是最大可表示幅度与最小非零可表示幅度的比值。以  表示的以上两种方法的动态范围是

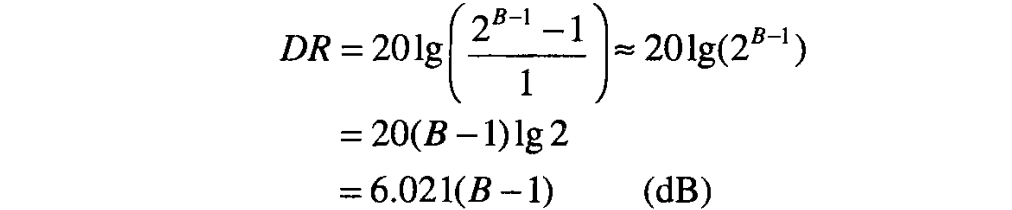
因此，每增加一位，可得到的动态范围大约增加  ，例如，  位量化器有  的动态范围，而  位量化器则有  的动态范围。当  大于或等于  位时，上式中由于近似而产生的  误差小于  ，一般情况都符合该条件。

除了考虑字长与编码外，必须确定对  进行赋值的规则，以得到允许的  值。两个常用的规则是取整或截断。这些操作的影响取决于是否采用了带符号幅度以及二进制补码编码操作。这种影响可以被归结为将  和  联系起来的有效量化器传递函数。

下图给出了传递函数的示意图。注意，不论是对数字表示取整的传递函数，还是对带符号幅度编码截断的传递函数，都关于第  象限以及第  象限的角分线对称。即关于  对称分布的输入信号，其量化误差也是关于零对称分布的，因而其均值为零。

但对于二进制补码编码进行截断的传递函数却不对称，因而其量化误差的均值是一个非零的正值。另外，量化后的信号将包含一个直流分量，但该分量不存在于被量化之前的信号中。在某些情况下，这一直流分量是非常明显的，尤其是在多普勒域的处理中，它会产生一个明显的虚假目标，或者使杂波功率增加。因此，我们更倾向于选择零均值量化误差的量化器。

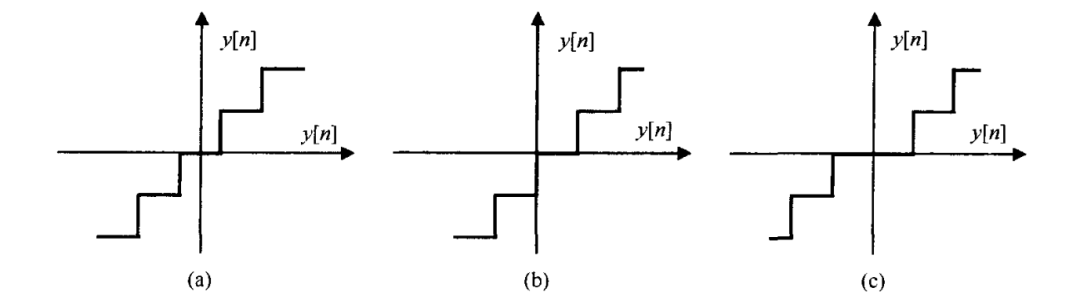
图（a）为二进制补码或带符号的幅度编码方法，取整量化的量化器传输函数；图（b）为二进制补码，截断量化的量化器传输函数；图（c）为带符号幅度编码，截断量化的量化器传输函数

一旦确定了量化器的特性，就必须确定量化步长  。  的选择受到两方面的限制。  的最大值应当落在量化器的动态范围，因此  应满足  。当给定量化器的量化字长时，就可以确定出  的最小值。

当不存在目标回波或杂波时，  完全是由接收器的噪声构成的。即使目标回波存在，也经常低于噪声电平，尤其当脉冲压缩处理之前采用  转换时。如果  太大，以至于量化器最低有效位（LSB）的输出不再因为噪声的存在而波动，而始终输出零，则信号信息将完全丢失。

确保噪声能够使最低位的值产生波动，就可以计算出  的最大值。它不可能同时满足这两个准则，以至于在许多实际情况下，为了避免对位于噪声电平处信号的抑制，就要接受量化器存在饱和的可能性。

为了更多地从数值基础上研究这些想法，假定  为零均值，标准差为  的高斯白噪声。那么，量化器的输出可以表示为如下输入信号和量化器误差  的和：

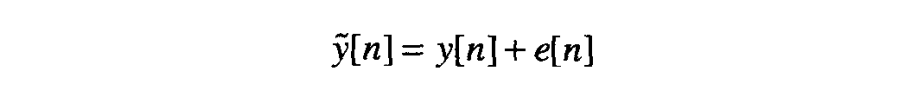
一般情况下，  被看做在区间  均匀分布的随机变量（因此，其方差为  ），同时其每个采样之间，及其信号  之间都不相关。信号与量化噪声比（SQNR）为

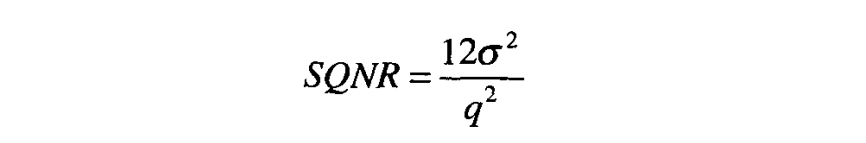
设  位量化器所表示的最大值被记为  ，同时为了简便起见，假设  足够大，从而满足  ，则  。以分贝表示的 SQNR 则变为

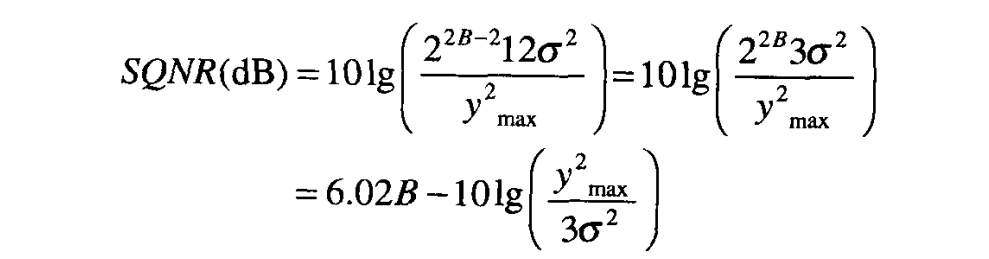
上式给出了一般性的结论，即量化器字长每增加一位，SQNR 就改善  。该结论被称为量化器噪声的线性模型，因为以分贝表示的 SQNR 是位数的线性函数。

当输入信号是方差为  的噪声时，量化器的输出方差  为  。定义参数  为  ，即为噪声标准差倍数的量化步长，从而可以得出用输入端噪声功率进行归一化的量化器输出端噪声功率为

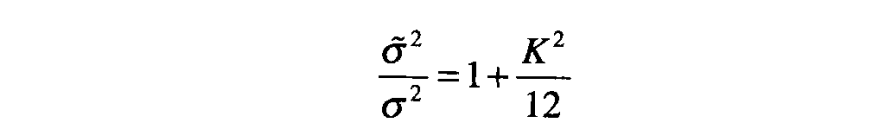
该等式是量化噪声线性模型的另外一种表达形式。所需的输出结果为  ，即量化过程没有使噪声的功率有太大的增加。

线性模型容易产生误导，因为它预测当  即量化步长增大时，输出信号的噪声功率也会随之连续增大。如前所述，因为当  变得足够大以至于输入信号不会触发 LSB 时，输信号将趋于零，这种情况被称为下溢。输出信号为零时其方差亦为零，该结果明显与上式相违背。

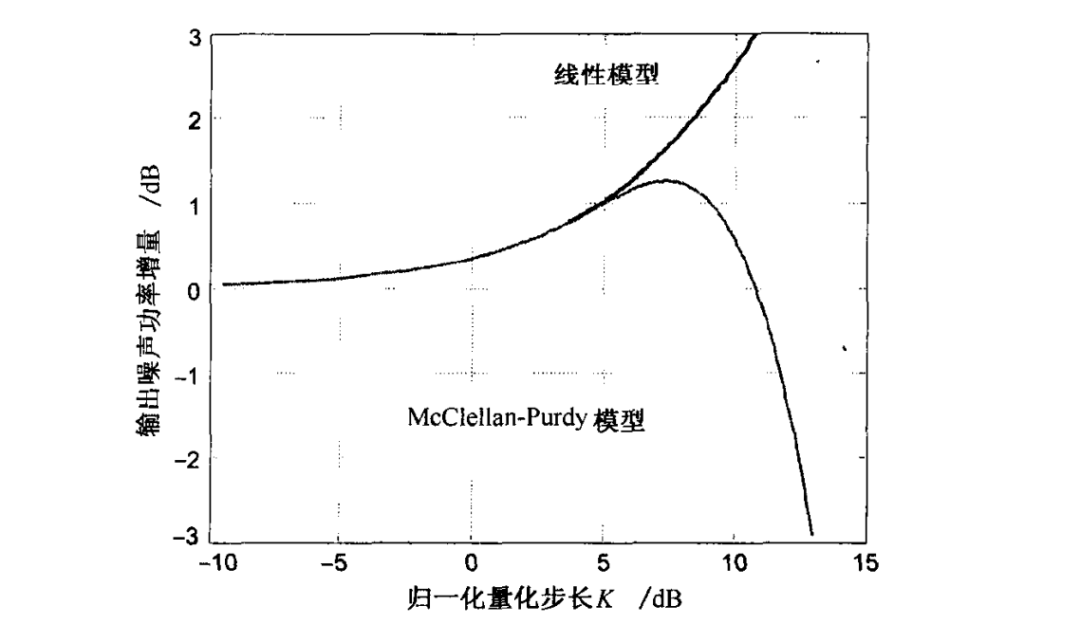
通过考察采样器实际输出信号的离散概率密度函数可以展开更贴近实际的分析。对给定的归一化步长  ，将量化层数设定为整数  ，从而使其满足  ，它可以保证忽略超过  的输入噪声，从而可以忽略潜在的饱和。由此，可以得到对输出功率的较好近似

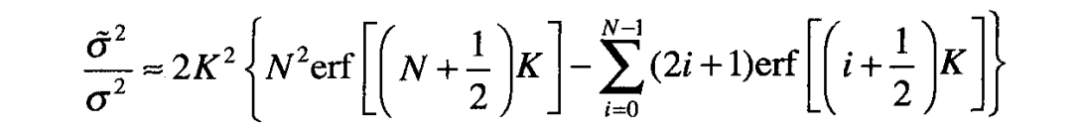
其中

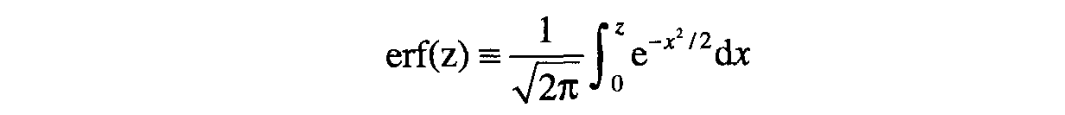
它是误差函数的标准定义。

下图同时给出了上式的 McClellan—Purdy 模型和线性模型。从 McClellan—Purdy 模型中可以清晰地看到随着量化步长的增大，输出噪声功率显著降低。从量化噪声角度考虑，对于附加的从  到  范围变化的量化噪声功率而言，合理的操作区域应该将  选择在  到  范围内（即  ）。通常将工作点选择为  ，即  ，这时量化器会使噪声功率增加到  。

到目前为止的分析均假设量化位数是无限的。对于有限的量化器位数  ，可表示的最大输出幅度值为  。大于该值的输入将被截取为  ，这种效应被称为饱和。

当  值减小时，相比于输入噪声功率量化步长会减小，从而更可能出现饱和。当饱和变得严重时，减小  值将不会使  趋于  。实际上，饱和会使输出的噪声功率小于输入的噪声功率，从而产生类似于由大  值引起的信号抑制效应。在量化步长取两个极端时对输出噪声功率所产生的联合信号抑制效应可以根据下式估计

－ The End －

版权声明：欢迎转发本号原创内容，转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理，相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请跟我们联系删除。我们致力于保护作者知识产权或作品版权，本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。

投稿/招聘/推广/合作/入群/赞助 请加微信：15881101905，备注关键词

“阅读是一种习惯，分享是一种美德，我们是一群专业、有态度的知识传播者