前面花了三节内容,把Buck各个级的传递函数给推导出来了,只需要把它们相乘,就可以得到环路的开环传递函数了。
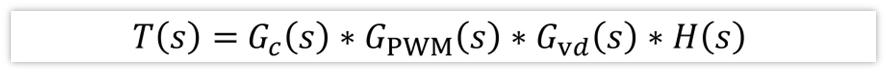
那有没有办法验证它们是否正确呢?这一节就来干这个事情。
验证方法
我打算使用LTspice进行仿真验证,方法是这样的:
1、搭好电路
使用分立器件搭建一个Buck电路,设定好输入电压,选定好电感,电阻,电容等器件。
2、根据公式直接画波特图
根据前面推导的公式,我们可以直接列出这个电路的开环传递函数的表达式,有了表达式,我们就可以直接根据表达式画出波特图。
3、测试得到波特图
我们直接仿真前面搭建的buck电路,从FB输入小信号,就跟我们现实中测试波特图一样,测量出环路的波特图。
4、对比
如果根据公式得到的波特图和测试出的波特图一样的话,就说明我们先前推出的公式是没问题的,即完成了验证。
下面开始验证
搭建buck电路
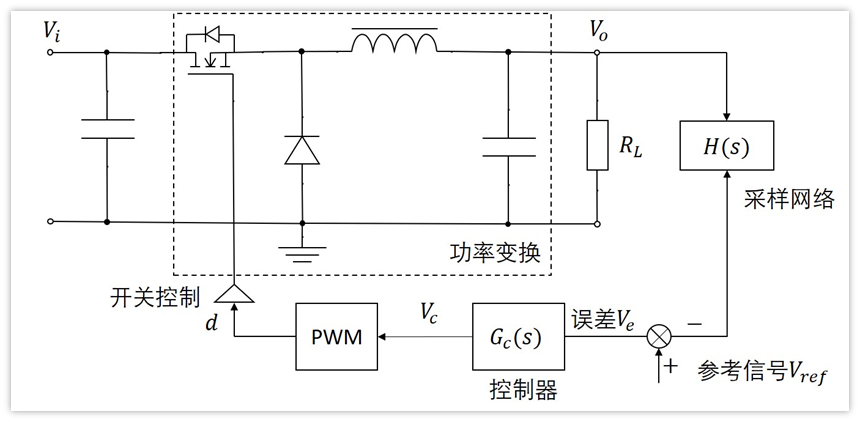
我们根据buck的系统框图,搭建电路如下:
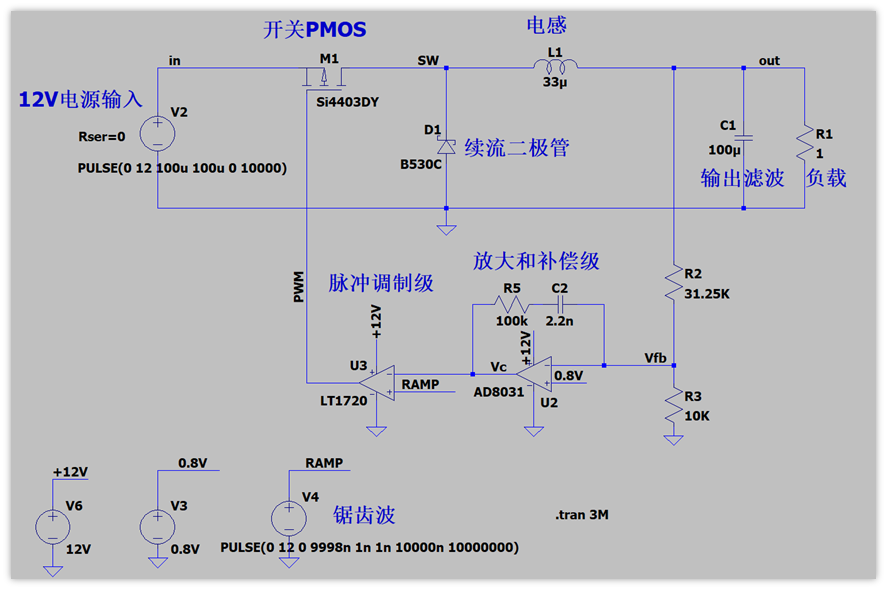
锯齿波RAMP使用电压源产生,锯齿波与放大和补偿后的信号做比较就能得到PWM了。周期为10us,即开关频率为100Khz,也就是说我这个buck的开关频率固定为100Khz。
类似于我们常用的buck芯片,Vfb设定为0.8V,我搭建电路的时候,是想输出3.3V电压的,所以设定R3=10K,R2=31.25K,根据分压,可以计算得到输出电压:Vout=0.8*(1+R2/R3)=3.3V
R5=100K,C2=2.2nF的取值我比较随意,只是随便试了几个值,看输出电压能够正常输出我想要的值就没有再改了,兄弟们也可以自己去试试别的值看看。
图中除了电阻、电容、电感之外,还用到了PMOS管Si4403,高速比较器LT1720,放大器AD8031,这几个器件选型也并没有特别的挑选。不过需要注意,比较器不要用放大器替代,速度会不够,无法正确的产生PWM信号。
我们运行下,输出波形如下图
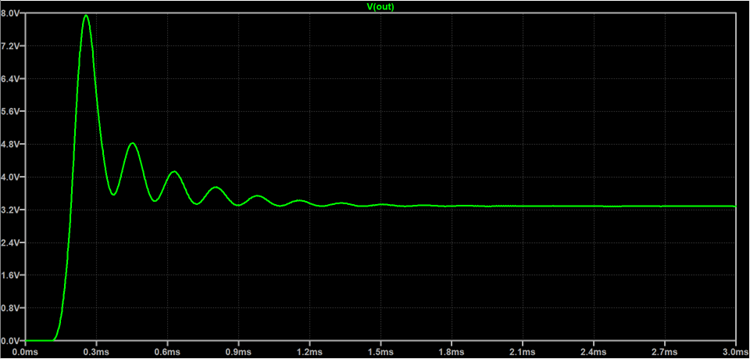
可以看到,输出在3ms之后稳定在3.3V,跟我们的设定值是一致的,说明这个搭建的电路算是正常跑起来了。
不过,也许会觉得刚上电的时候输出电压会飙到8V有问题,这个其实因为我们对初始状态并没有额外的处理。另外一方面,我们测量环路,只测量稳定状态时的,因此,我们只需要测上电3ms后的环路就行,也不影响我们的目的。
电路已经搭起来了,那就进入第2步——根据公式得到波特图。
根据公式直接画波特图
根据“两种误差放大器的传递函数”这一章节可知,反馈级和误差放大级的传递函数表达式如下:
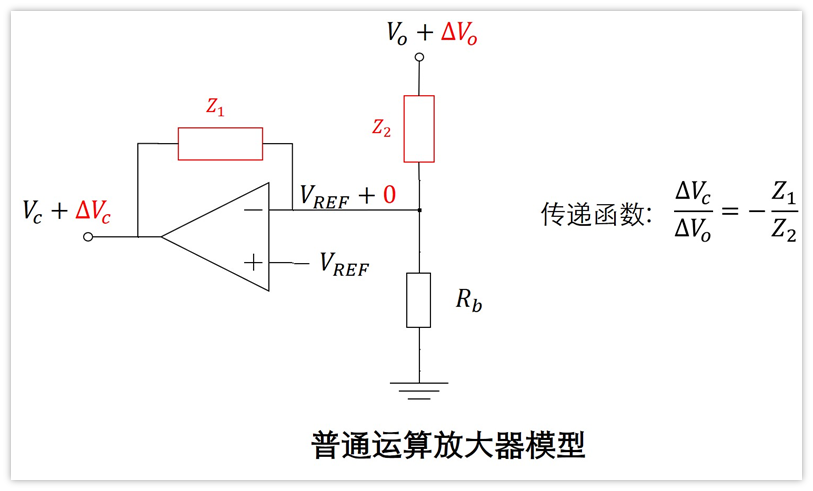
代入到前面构建的电路中就可以求得采样和放大补偿级的传递函数如下图:
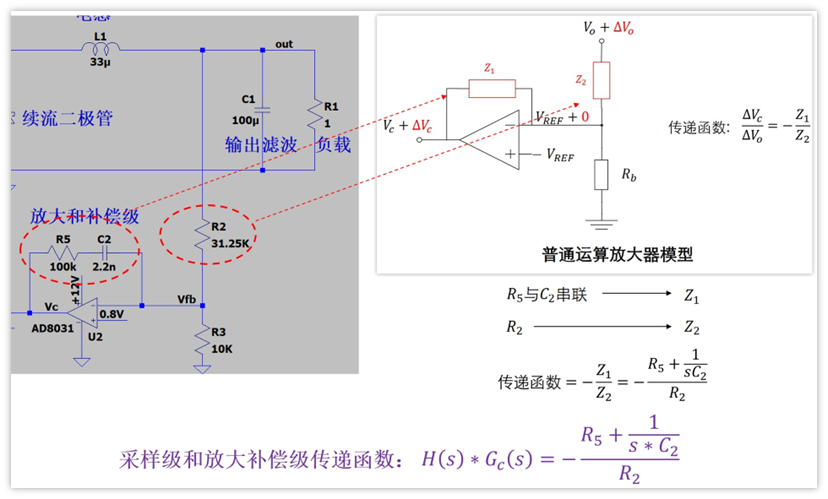
由前面章节“脉冲调制级传递函数Gpwm(s)”可知,传递函数表达式如下:
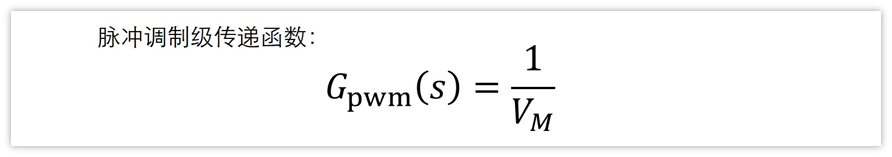
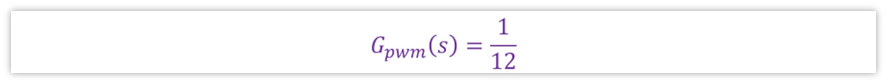
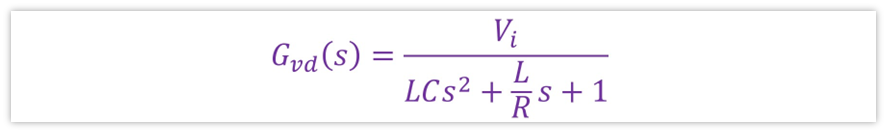
这里面L为电感,C为输出滤波电容,Vi为输入电压,R为负载。代入到我们构建的BUCK电路,那么就是L为L1=33uH,C为C1=100uF,R为R1=1Ω,即Gvd表达式为:
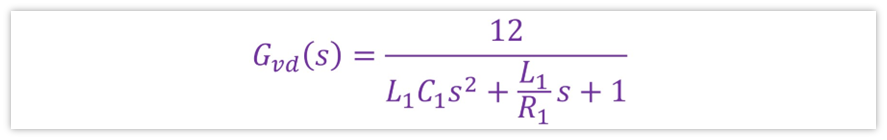
好了,我们现在4个级的传递函数已经求出来了,我们把它们全部乘起来就是开环传递函数了。

有了表达式,我们就可以直接画出开环传递函数的波特图了,这里我们可以直接使用LTspice就能达到目的,具体方法我专门写了个小文章介绍,见下面链接。
如何使用LTspice画已知传递函数的波特图
我们使用LTspice直接画出上面开环传递函数的表达式对应的波特图,需要代入电路图中的各个参数值(L1=33uH,C1=100uF,C2=2.2nF,R1=1Ω,R2=31.25K,R5=100K)。
最终波特图如下图:
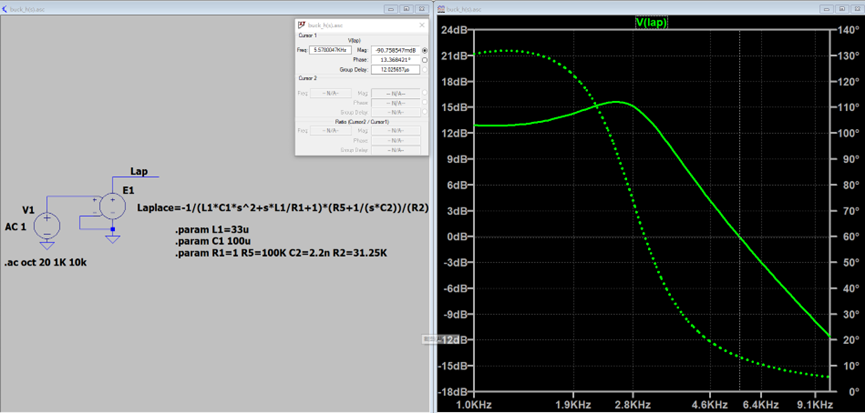
从图中可以看到,穿越频率是5.56Khz
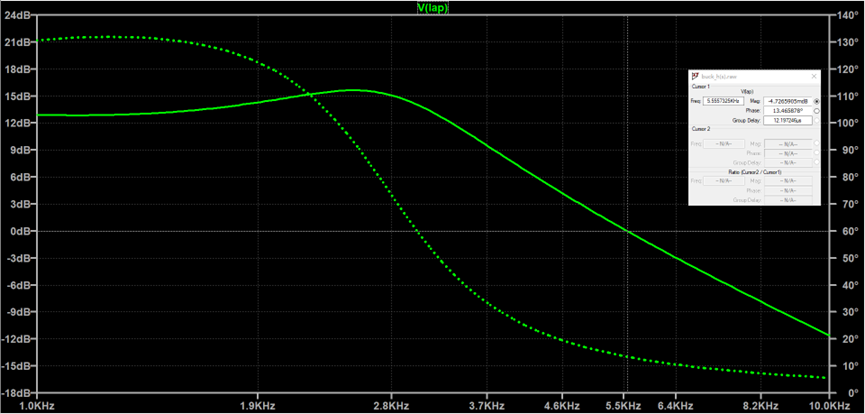
以上就是先计算出开环传递函数的公式,然后根据公式直接画图得到的波特图。写的比较啰嗦,主要是希望想亲自试一下的同学,能照着步骤很快能搞出结果来。
公式法已经有了,下面使用测试的方法来得到波特图。
测试得到波特图
使用LTspice测试得到波特图有点费劲,我在这里卡了很久,这也是我最近一段时间没有更新的原因之一,不过最终也总算是在一位网友的帮助下解决了我的问题。
为了让兄弟们不至于在这一步卡住,我尽量说得清楚一些。
测试得到波特图的原理,其实就跟我们现实工作中拿仪器测试环路一样。
通过给环路注入正弦波小信号,然后测量输出信号,输出信号与输入信号幅度的比值就是环路的增益,两者之间的相位差异就是环路的相移。
注意,小信号的频率是变化的,因为我们的波特图,描述的就是在不同频率下,环路的增益和相移的关系。所以我们需要测量很多的频点,分别测量每一个频点对应的增益和相移,然后将它们连成线,就构成了波特图。如果正弦波小信号只有一个频率,那么只能得到一个点。
这是不是有点类似AD采样?如果我们想得到非常平滑的曲线,那么就需要采样更多的点,那么也就意味着更高的采样率。
使用LTspice也是一样,如果参数设置不合理,可能会造成仿真时间特别的长,这一点需要特别注意,我后面也会详细介绍。
具体现实中怎么测试环路,我在B站上面看到一个视频,说得还比较清楚,链接是这个:
https://www.bilibili.com/video/BV1tt4y117vL?spm_id_from=333.337.search-card.all.click
感兴趣可以去瞅瞅,还比较好
下面是视频的一章截图,测试原理是一目了然的了。
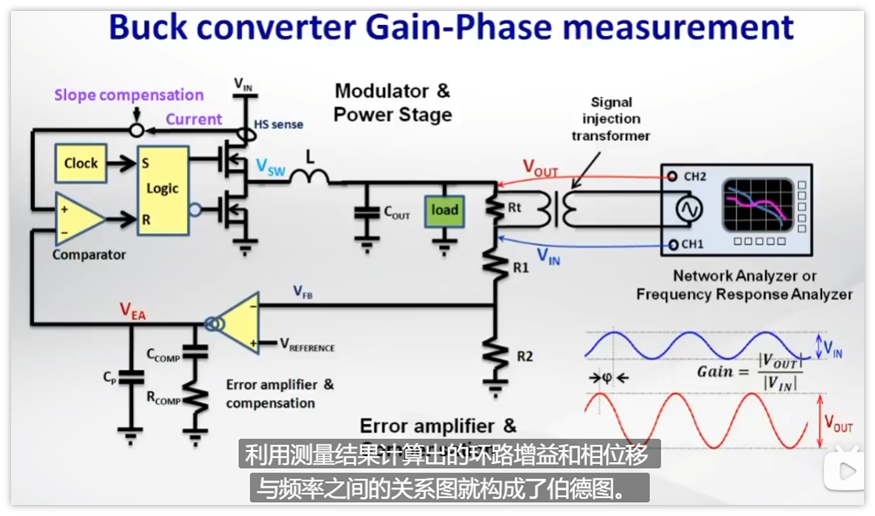
以上就是现实工作中通过测试的方法得到波特图的原理。
下面进入正题:LTspice如何通过测试方法,得到前面构建的Buck电路的波特图呢?
首先,在Vout与上面的分压电阻之间加一个电压源,用于注入正弦波小信号。注意,里面的频率是一个变量freq,因为我们要测很多频率点,幅度是20mV,不能太大,太大会影响电路正常工作。
电路图如下图所示:
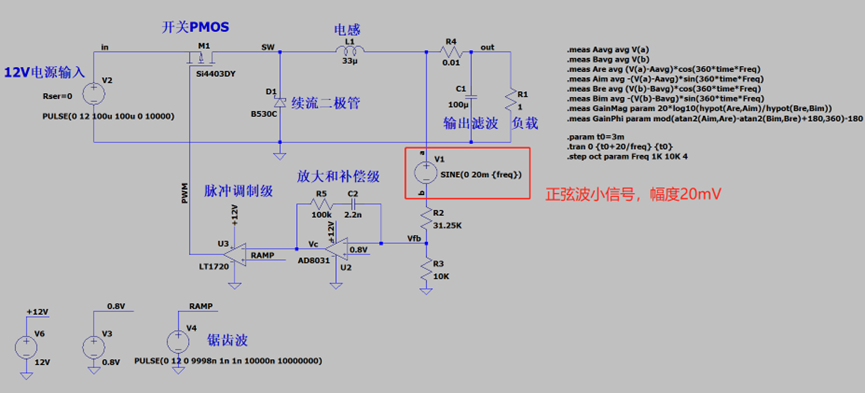
如果细心的话会发现,我还加了一个0.01Ω的电阻R4,之所以加这个,就是我踩的一个坑。如果没有R4,那么网络a就和网络out是一个网络,后面执行的时候就一直有问题,所以这个R4仅仅起一个隔离的作用,不让同一个网络被取了两次名字。
右面的spice命令加了很多,看着有点费劲,其实也不难,意思大致是这样的:
.meas Aavg avgV(a)-----测量a点电压平均值Aavg.meas Bavg avgV(b) -----测量b点电压平均值Bavg.meas Are avg(V(a)-Aavg)*cos(360*time*Freq) -----测量a点交流电压实部平均值Are.meas Aim avg-(V(a)-Aavg)*sin(360*time*Freq) -----测量a点交流电压虚部平均值Aim.meas Bre avg (V(b)-Bavg)*cos(360*time*Freq) -----测量b点交流电压实部平均值Bre.meas Bim avg-(V(b)-Bavg)*sin(360*time*Freq) -----测量b点交流电压虚部平均值Bim.meas GainMagparam 20*log10(hypot(Are,Aim)/hypot(Bre,Bim)) -----测量增益.meas GainPhiparam mod(atan2(Aim,Are)-atan2(Bim,Bre)+180,360)-180-----测量相位
如果不懂也没关系,只需要将电路上面的2个测量点命名为a和b,然后将这一段spice命令粘上即可。
Freq是频率,是一个变量,因为会测量很多频率点。
.param t0=3m-----设置参数t0=3ms.tran 0 {t0+20/freq} {t0}-----运行t0=3ms后开始测试,测试20个周期.step oct paramFreq 1K 10K 4-----测量频率范围为1K~10Khz,每倍频程测量4个点
t0是系统开始运行到达到稳定状态所需要的时间长度。前面我们运行的时候,已经知道了3ms后系统达到稳定,所以我们这里设置为3ms。注意,不同的系统达到稳定的时间是不同的,要根据实际情况来。不过也需要注意,设置太长会造成仿真时间太长。
频率测量范围我选定的是1K~10K,之所以是这个范围,是因为我已经提前知道了穿越频率是5K左右,所以没有把频程设置很大,因为设太大会造成仿真时间比较长。当然,兄弟们可以自己改一改试一试。
仿真运行
一切准备就绪,我们运行一下,基于当前的设置,我计时了一下,运行时间大概是3分钟(不同电脑配置可能不同)。
运行过程中,我们可以在窗口左下方看到仿真进度,左下角可以看到Run:1/15;
15表示的是会测量15个频点,1表是正在测量第一个频点。

运行结束之后,波形窗口看不到任何波形,因为还需要操作下面几步:
1、在波形窗口点击鼠标右键,选择“View”菜单下面的“SPICE Error Log”
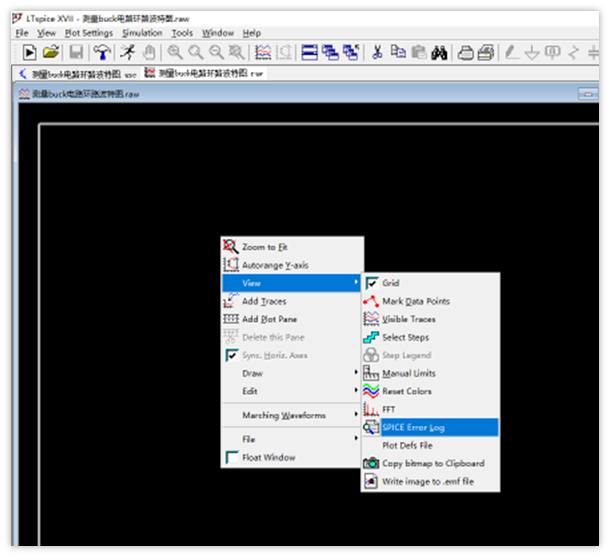
2、在弹出的log窗口里面,点击鼠标右键,选择“Plot .step’ed .meas data”,在弹出的窗口选择“是”
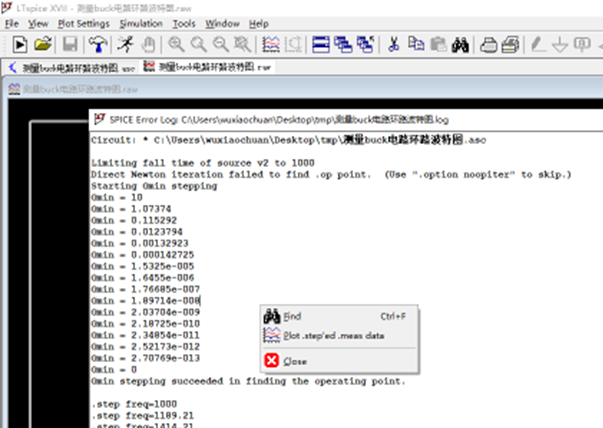
3、在弹出的窗口中点击鼠标右键,选择“View”菜单下面的“Visible Traces”
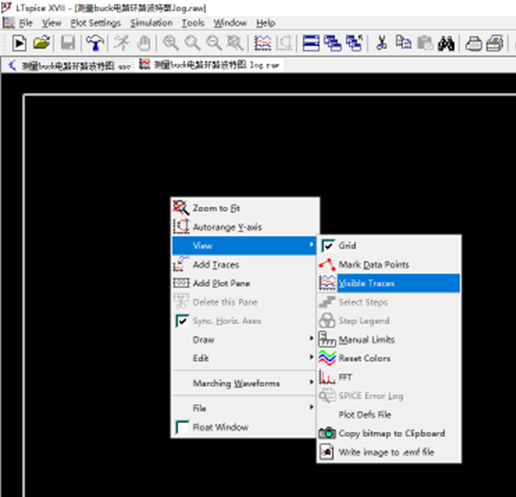
4、在弹出的窗口里面选择“gain”,就可以生成波特图了
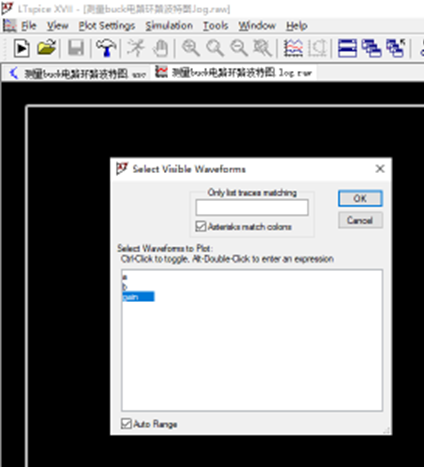
生成的波特图如下:
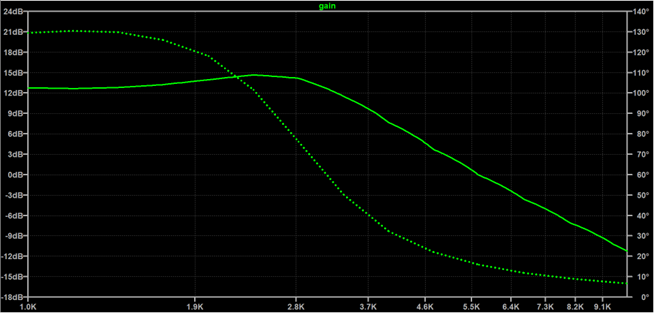
以上就是采用测试的方法得到波特图的全过程了,有点繁琐,我也是折腾了比较久,感兴趣的同学可以自己玩一玩,相关源文件我文末会分享出来。
至此,公式直接画出的波特图和测试法得到的波特图都已经出来了,我们下面对比看看它们的差别。
波特图对比
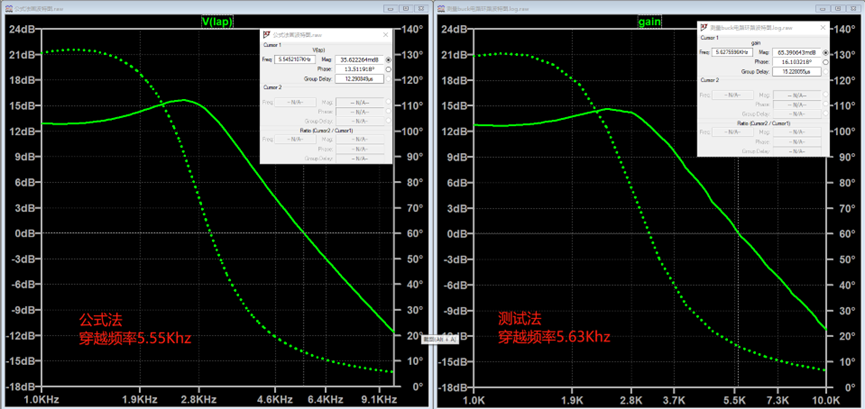
可以看到,二者波形基本一样,验证了我们开篇的目的:我们推导的传递函数是正确的。
小结
本节内容就写到这里了,主要是使用LTspice进行仿真验证前面推导的公式,不过这个仿真相对于以前来说还是比较复杂的,需要折腾一下。
相关源文件我已经放到了网盘,可以在我的微信公众号“硬件工程师炼成之路”后台回复“炼成之路”。
东西有点多,文件放置在目录:电源/开关电源传递函数/Buck电源环路仿真实验验证
推荐阅读:
1、我写的东西都在这里了
2、手撕Boost!Boost公式推导及实验验证
3、手撕Buck!Buck公式推导过程