之前被安排了活,一个局部区域机器运动控制的工作,大致是一个机器位于一个极限区域时候,机器要进入一个特殊的机制,使得机器可以安全的走出来。其中用到了bezier曲线进行优化路径,今天写一下,正好也给大家分享一下工作和实践的情况。
作者:良知犹存
转载授权以及围观:欢迎关注微信公众号:羽林君
或者添加作者个人微信:become_me
线段都可以被拆分成两个坐标的差来表示,如下面一阶的贝塞尔曲线,P0到P1,可以用一个t进行拆分这段线,分别是线段 t(P0~P1)、线段 1-t(P0~P1),P0和P1叫做, 这条条贝塞尔的两个控制点,而贝塞尔曲线至少要有两个控制点(就是下面的这条直线,一阶贝塞尔曲线)。在贝塞尔曲线与控制点位置相关,这意味着在曲线生成过程中,我们可以通过调节控制点的位置,进而调整整个曲线。
贝塞尔的阶数和次数是一样的,二阶贝塞尔,三个点,最高次数二次。例:二阶贝塞尔:三个点,两个线段,以所有等比的点组合成的曲线叫做二阶贝塞尔曲线。
接下来给大家介绍一下贝塞尔曲线的推导工程,也比较简单,并且网上的介绍也挺多的:
一阶: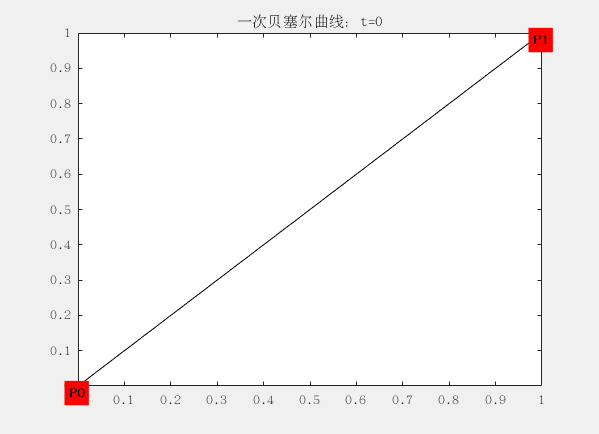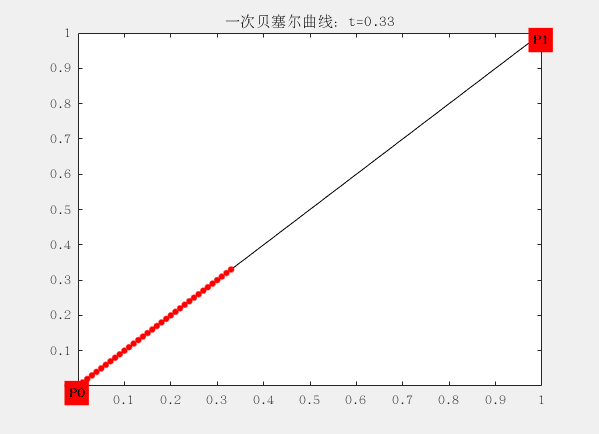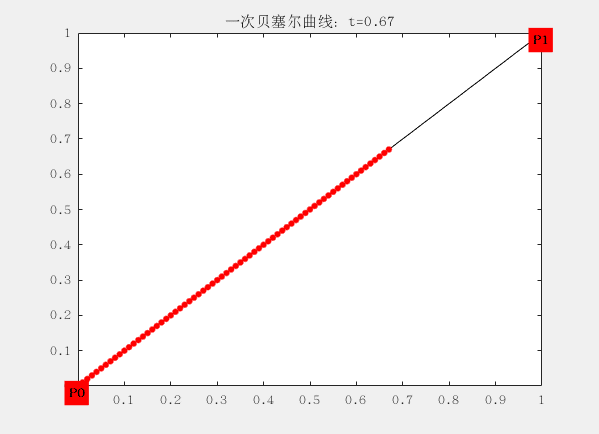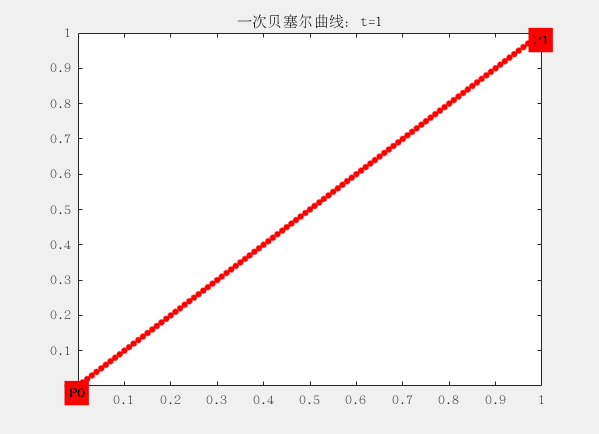
这里面有两个控制点为 ,对应的曲线方程为:
tϵ[0,1] 这个方程可以理解为,从出发,朝着的方向前进的距离,从而得到了点B(t)的位置。t从0逐渐递增到1,这个过程完成,就成了我们所看到的曲线。
另外,之所以是一阶贝塞尔曲线是因为方程是关于t的一阶多项式,多阶也是一样。
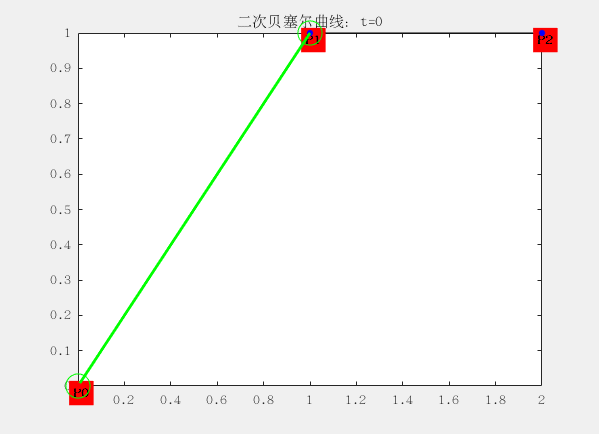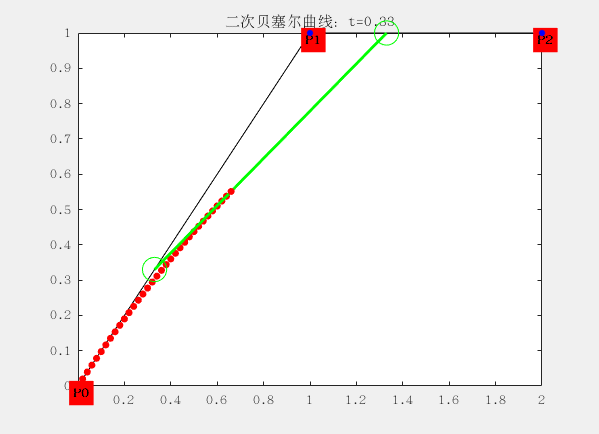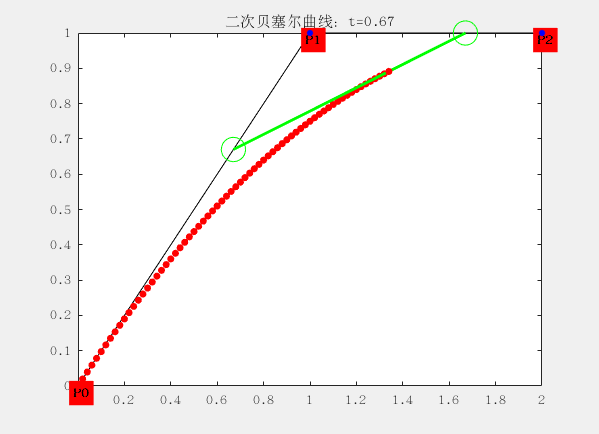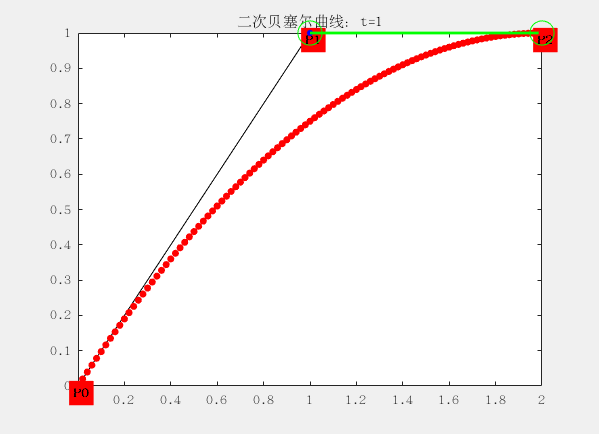
二阶:有三个控制点,这里的 P0、P1、P2 分别称之为控制点,曲线的产生完全与这三个点位置相关。
与一阶有些区别就在于三个控制点形成两个线段,每个线段上有一个点在运动,于是得到两个点;再使用两个点形成一个线段,这个线段上有一个点在运动,于是得到一个点;最后一个点的运动轨迹便构成了二阶贝塞尔曲线。
 对应的曲线方程为:
对应的曲线方程为:
这是一条迭代公式,每次迭代都会少掉一个“点”。
最后得:
三阶:有四个控制点
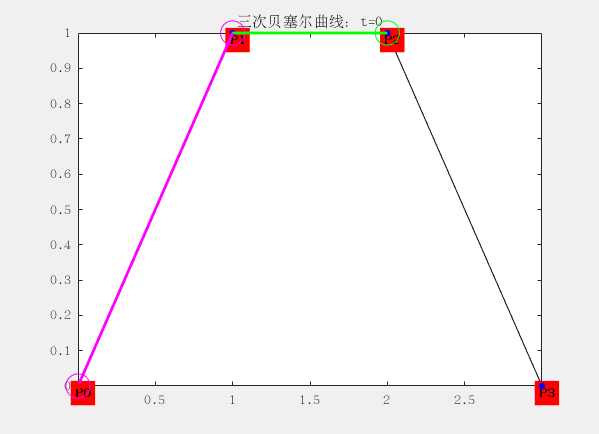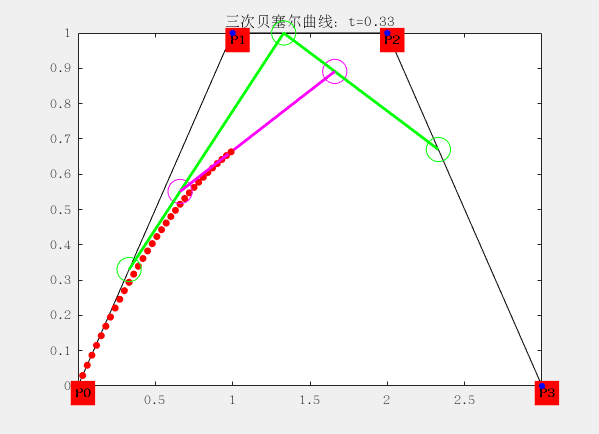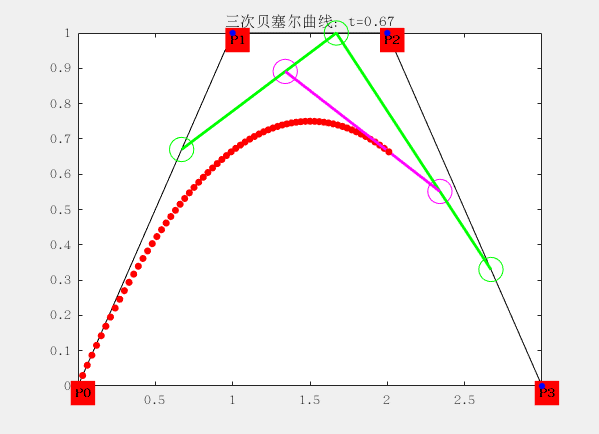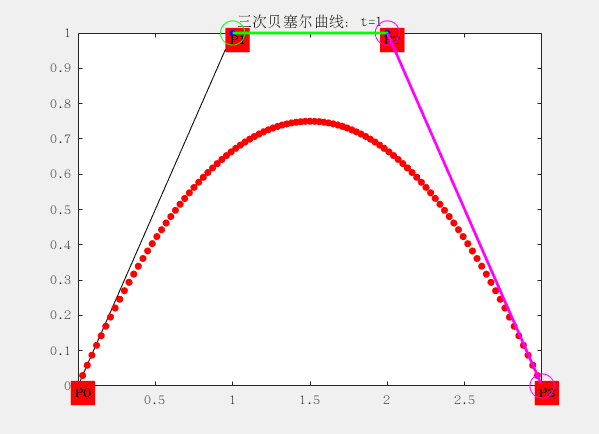
设控制点为P0,P1,P2和P4,曲线方程为:
配图这是matlab生成的gif动画,大家想要的也可以找我,代码私发给大家。
N阶:
我们发现,实际上是每轮都是 n 个点,形成 n-1 条线段,每个线段上有一个点在运动,那么就只关注这 n-1 个点,循环往复。最终只剩一个点时,它的轨迹便是结果。
如此一来,你会发现贝塞尔曲线内的递归结构。实际上,上述介绍的分别是一阶、二阶、三阶的贝塞尔曲线,贝塞尔曲线可以由阶数递归定义。
N阶贝塞尔曲线公式:
贝塞尔曲线在动画中有应用,前端以及一些其他显示要求;此外在路径规划过程中,也会使用贝塞尔曲线进行规划好路径再优化,我就是使用了后者进行优化规划好的路径,使得机器行走更加顺畅,不过使用中大家需要按照机器实际相应来进行调整t的精度以及阶数。
由于贝塞尔曲线本身的数学表达式便是一条递归式,所以决定采用递归的方式来实现。代码如下,BezierCurve函数实现贝塞尔曲线迭代,UseBezierOptimizePath函数的第二个参数进行控制使用的阶数,最后调用opencv实现可视化效果。
#include
#include
#include
#include
using namespace cv;
using std::cout;
using std::endl;
using std::vector;
template
T BezierCurve(T src)
{
if (src.size() < 1)
return src;
const float step = 0.003;//1.0/step
T res;
if (src.size() == 1) {//递归结束条件
for (float t = 0; t < 1; t += step)
res.push_back(src[0]);
return res;
}
T first_part{};
T second_part{};
first_part.assign(src.begin(), src.end() - 1);
second_part.assign(src.begin() + 1, src.end());
T pln1 = BezierCurve(first_part);
T pln2 = BezierCurve(second_part);
for (float t = 0; t < 1; t += step)
{
typename T::iterator::value_type temp{};
temp += pln1[cvRound(1.0 / step * t)] * (1.0 - t) ;
temp += pln2[cvRound(1.0 / step * t)] * t;
res.emplace_back(temp);
}
return res;
}
template
T UseBezierOptimizePath(T path,uint8_t order_number)
{
if(path.size() < order_number)
return {};
T new_path{};
for(uint8_t i=0;i {
T tmp = BezierCurve(T(&path[i],&path[ i + order_number]));
new_path.insert(new_path.begin(),tmp.begin(),tmp.end());
}
return new_path;
}
int main(int argc, char const* argv[])
{
while (1) {
cout<< endl;
cout<< endl;
cout<< endl;
vector path;
RNG rng;
for (int i = 1; i <8; i++)
path.push_back(Point2f(i * 800 / 8, random() % 800));//rng.uniform(0,800)));//cvRandInt(rng) % 800));
Mat img(900, 1200, CV_8UC3);
img = 0;
for(uint8_t i =0;i < path.size() -1;i++)
{
cout<< path[i]<< ","<< endl;
line(img,Point(path[i].x, path[i].y),Point(path[i+1].x, path[i+1].y), Scalar(255, 0, 0), 16, LINE_AA, 0);
}
cout<< endl;
// imshow("line", img);
for (int i = 0; i < path.size(); i++)
circle(img, path[i], 3, Scalar(0, 0, 255), 10); //BGR
// vector bezierPath = bezierCurve(path);
vector bezierPath = UseBezierOptimizePath(path,4);
for (int i = 0; i < bezierPath.size(); i++) {
// circle(img, bezierPath[i], 3, Scalar(0, 255, 255), 3); //BGR
img.at(cvRound(bezierPath[i].y), cvRound(bezierPath[i].x)) = { 0, 255, 255 };
// printf("pose(%f %f)\n",bezierPath[i].x,bezierPath[i].y);
imshow("black", img);
// waitKey(10);
}
if (waitKey(0) == 'q')
break;
}
return 0;
}
显示效果如下:
三阶
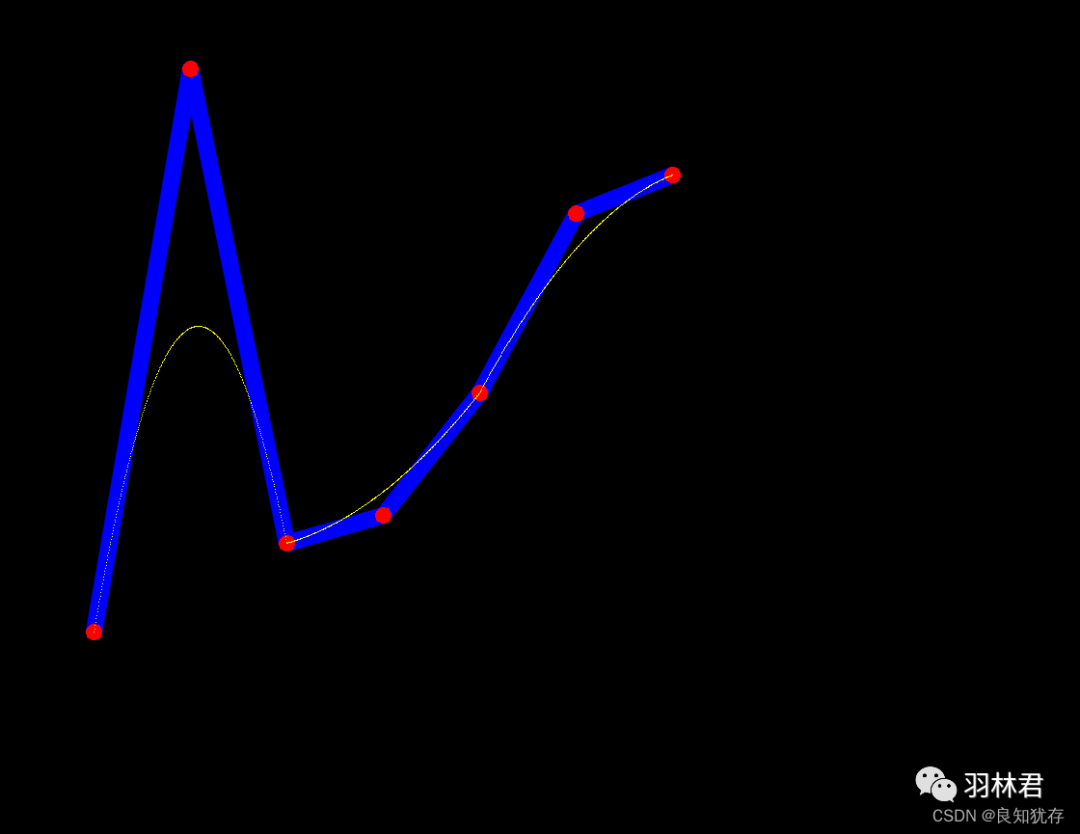
四阶
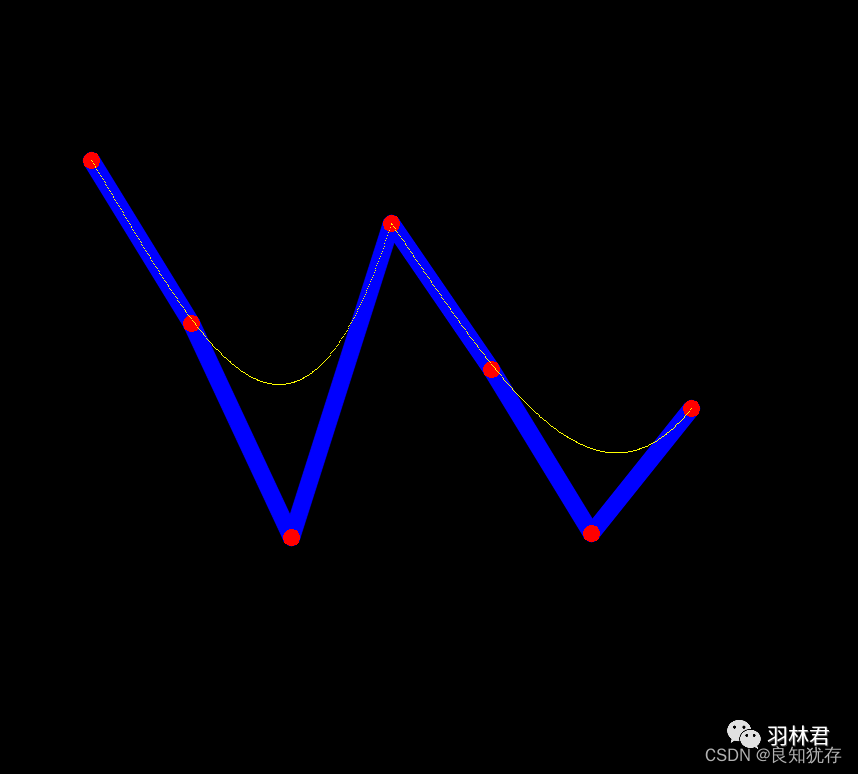
这就是我自己的一些设不贝塞尔曲线的使用分享。如果大家有更好的想法和需求,也欢迎大家加我好友交流分享哈。
作者:良知犹存,白天努力工作,晚上原创公号号主。公众号内容除了技术还有些人生感悟,一个认真输出内容的职场老司机,也是一个技术之外丰富生活的人,摄影、音乐 and 篮球。关注我,与我一起同行。
‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧ END ‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧
推荐阅读
【1】jetson nano开发使用的基础详细分享
【2】Linux开发coredump文件分析实战分享
【3】CPU中的程序是怎么运行起来的 必读
【4】cartographer环境建立以及建图测试
【5】设计模式之简单工厂模式、工厂模式、抽象工厂模式的对比
本公众号全部原创干货已整理成一个目录,回复[ 资源 ]即可获得。
