来源 | 雷达信号处理matlab

智库 | 云脑智库(CloudBrain-TT)

云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向

声明 | 本号聚焦相关知识分享，内容观点不代表本号立场，可追溯内容均注明来源，若存在版权等问题，请联系(15881101905，微信同号)删除，谢谢

由前期讲述可知，雷达系统具有两种截然不同的空间采样类型。一种类型是相控阵天线的设计。相控阵天线在各个阵元处对到来的波前进行采样。因此，这些阵元的间距要满足对各种入射角波前采样的要求。

另一种关心的是波束指向。机械扫描或者电扫描的天线都能够改变其波束指向。由于波束扫描需要对空间区域进行搜索或绘图，因此，要确定在雷达发射下一个脉冲之前，允许雷达扫描多远，以使外部环境被充分采样。

空间频率

在涉及电磁波传播的研究中，空间频率是一个重要概念，在我们分析空间采样和空时自适应处理时必须采用这个概念。

如下图所示，考虑一个波长为  、传播速度为  、沿  正方向传播的正弦脉冲。在固定空间位置  的观测者将以时间间隔（周期）  接连地观测到波峰，所以这个波的时间频率为    或者    。

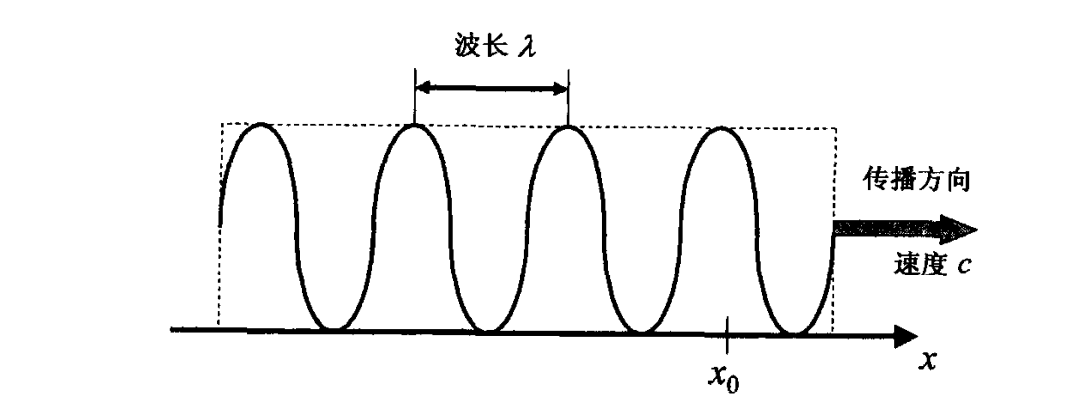
同样，我们也可以定义空间周期，它是固定观测时刻空间中相邻两个波峰之间的间隔。在上图中，脉冲的空间周期显然是  米，所以空间频率就是每米  个周期，或者每米    。通常将后一个量称为脉冲的波数，并用符号  来表示它。

由于通常情况下空间位置和速度是三维矢量，所以波数也是三维矢量。为简单起见，我们考虑下图给出的上图的二维情况。在  平面内脉冲的传播是沿着一个角度进行的，在传播方向，波数仍为  。

然而，在  正方向测量，波数为  ，其中  为相对于  轴正方向测得的脉冲的入射角。同样，上述信号在  方向的波数为  。注意当  趋近于  时，  方向的波长趋近于  ，所以  趋近于  。

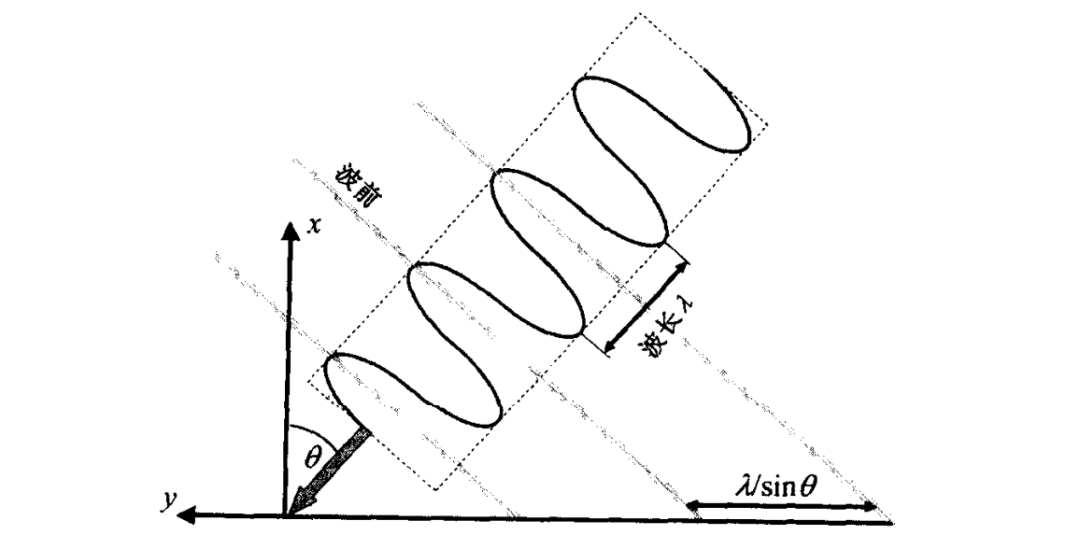
我们可以直接从上面的二维空间扩展到三维空间。显然，总的波数与各个分量的关系如下： 

总波数总是等于  。注意，时间频率是与方向无关的，它总是等于  。

固定相位单元间距

下图中是一个间隔为  的均匀线阵。

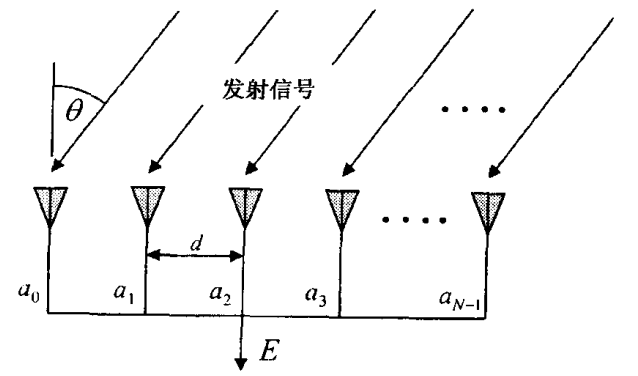
如图所示，一波长为  的射频信号以偏离阵列法向  为波达方向射向阵列天线，则其波数（空间角频率）为 

对应的空间频率为 

波达角  可以从  到  变化，则空域频率带宽为 

周根据奈奎斯特准则，可以得到所需的空间采样间隔 

因此，为避免空间频率混叠，阵列中阵元的间距应不大于  。

天线波束间隔

考虑某个  波束宽度为  ，或者第一零点间波束宽度（详情请看#快时间维采样#）为  的可控天线或扫描天线。每个发射脉冲都对天线所指方向上的环境反射性进行采样。

如果要对角空间某个区域进行搜索，就会产生以下问题：应该以多密集的角度对空间进行采样？即在下一个脉冲发送之前，天线应转过多大的角度？当然，以较小的角度作为采样间隔能更好地反映被搜索空间的特性，但需发送较多的脉冲，从而会花费更多的搜索时间。

相关文献指出，天线的电压起伏图会压制与天线视轴夹角大于  （或  ）的回波。因此，为了充分地对天线扫描场景的反射体进行采样，我们直观地希望每当扫描超过  （或者  ）整数倍时，就重新进行一次测量。奈奎斯特准则可以应用于该空间的采样问题，从而使我们的期望量化。

由前面的内容可知，对于某个固定距离，以角度表示的被测反射系数是距离平均反射性和单程天线功率方向图的卷积。为简单起见，对只有一个角度维且对称的天线图，我们可以得到其等价表达式 

其中，  表示卷积，  是在距离  处以角度  （方位角或者俯仰角）为函数的复相干接收器的输出，  是在距离  处的平均距离反射系数，而  是角度维的单程功率方向图。

该式也可以被解释为  在角度维的傅里叶变换是天线方向图傅里叶变换和平均距离反射系数傅里叶变换的乘积。

我们知道理想矩形孔径天线的单程天线功率方向图为 

定义  ，  ，则上式可被改写为 

可以看出，这是一个平方  函数。

根据傅里叶变换对的知识，可得其傅里叶变换是归一化变量  的三角函数，其中  为天线孔径的空间尺寸。下图对该函数进行了描述。

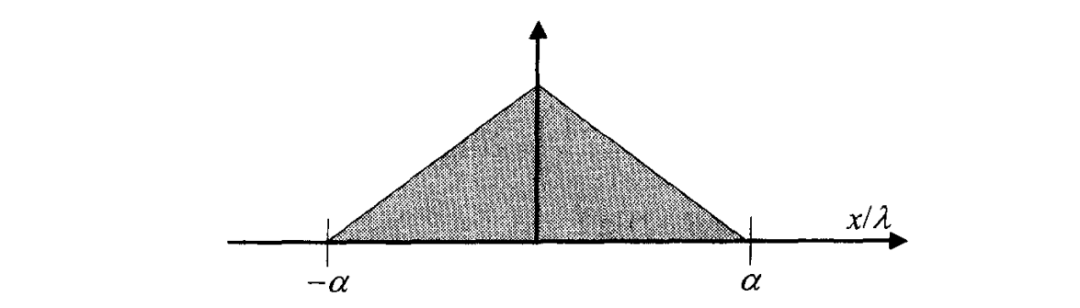
由于天线图的傅里叶变换的宽度为  ，考虑到  ，以  表示的奈奎斯特采样间隔必须满足 

为了把  转换成以  为单位的采样间隔，考虑微分  ，则  。因此，  域的小间隔  近似对应于  域的间隔  。当  时，  取得最小值，此时  。因此，以角度表示的采样间隔为 

这就是尺寸为  ，均匀照射的矩形孔径在角域的奈奎斯特采样间隔。

这一结果也可以用  波束宽度表示。孔径天线的  波束宽度为 

在均匀照射的情况下，  。则 

当  时，根据上式得出的奈奎斯特采样速率是  波束宽度的  倍，即每个  带宽中有  个样本。实际中，许多系统在角域的采样大约为每  带宽  个样本。这种搜索间隔在角域是欠采样的，至少从奈奎斯特准则角度是欠采样的。

以上由均匀照射孔径得出的结论，可以推广到全孔径天线。对于一个尺寸为  的有限孔径，可以通过改变孔径的照射函数来获得不同的功率方向图（例如，以加宽主瓣为代价获得较低的旁瓣），常常通过类似信号处理中加窗操作的方法使其逐渐降低。

这些天线功率方向图的傅里叶变换仍然是相应照射函数的自相关。由于孔径照射函数的支撑区有限，所以其自相关函数在  域被限制在  宽度范围，如上图所示，只是函数的细节形状有所改变。因此，  可以应用于任何有限孔径天线。

其差别是，不同的照射函数对应不同的  值。低旁瓣天线的  值范围约为  到  ，对应的奈奎斯特采样速率近似为每  波束宽度有  到  个样本。

附录：最大释然法的DOA估计

最大似然及子空间拟合算法简介

众所周知，贝叶斯方法是基于统计理论的一种经典方法，适合于有关参数估计问题。最大似然（Maximum Likelihood，ML）估计方法就是贝叶斯估计方法的一种特例，是在已知白噪声情况下的贝叶斯最优估计。

在 ML 算法中，观测所得信号的似然函数被定义为含有未知参数的条件概率密度函数，目的是选定未知的参数以使得该似然函数尽可能大。通过最大化似然函数求出的解都被认为是未知参数的一个估计。

子空间拟合（SF）的概念是 20 世纪 90 年代之后提出的，其基本思想在于构造这样一个事实，即阵列流型矩阵与阵列接收数据的子空间之间存在一个拟合关系。SF 算法与 ML 算法的相同点在于：这个拟合关系也是一个最大或最小化的似然函数求解问题，都可通过最大或最小化似然函数求出未知参数的一个估计。

两者的不同点在于对象不同，对于确定性最大似然（DML）算法而言，其实质是接收数据与理想数据的一个拟合，而 SF 算法则是阵列流型矩阵与接收数据的子空间之间的一个拟合。

ML 和 SF 算法在空间谱估计领域中已有大量的研究成果，这类算法主要包括最大似然（ML）算法、多维 MUSIC 算法、加权信号子空间拟合（WSSF）算法以及加权噪声子空间拟合（WNSF）算法。

在空间谱估计中，这类算法的思想简单、估计性能优越，但其算法的实现过程却很复杂。ML 和 SF 算法的求解过程涉及到一个多维的非线性优化问题，运算量相当大。

最大似然算法基本概念

最大似然估计是一种统计方法，它用来求一个样本集的相关概率密度函数的参数。“似然”是对 likelihood 的一种较为贴近文言文的翻译，“似然”用现代的中文来说即“可能性”。故而，若称之为“最大可能性估计”则更加通俗易懂。

给定一个概率分布  ，假定其概率密度函数为  ，其分布参数为  。但是，我们可能不知道  的值，我们如何才能估计出  呢？

一个自然的想法是从这个分布中抽出一个具有  个值的采样  ，然后用这些采样数据来估计  。通过利用，我们就能计算出其概率：

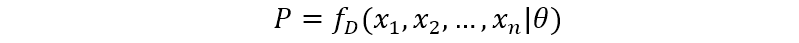
最大似然估计会寻找关于  的最可能的值（即在所有可能的  取值中，寻找一个值使这个采样的“可能性”最大化）。

最大似然准则

根据入射信号模型的不同，基于最大似然的波达方向估计方法分为确定性最大似然（Deterministics ML，DML）法和随机性最大似然（Stochastic ML，SML）法两大类型。随机性最大似然法也称统计最大似然法。

确定性最大似然法：在这种方法里，入射信号序列  假定为确定性信号，待估计的未知参数是输入序列和信道矢量  ，即  。在这种情况下，未知参数的维数随观测数据量的增多而增大。

随机性最大似然法：在这种方法里，入射信号序列  假设为一具有已知分布的随机过程（通常假设为高斯随机过程），而且唯一待估计的未知参数就是信道矢量  ，即  。在这种情况下，未知参数的维数相对于观测数据量是固定的。

由前面的讨论可知，窄带远场信号的 DOA 数学模型为

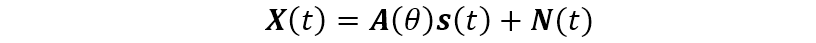
即

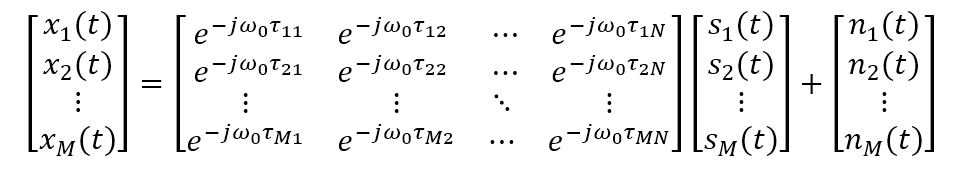
式中，  为阵元个数，  为信源个数。

对于间距为  的均匀线阵，且以最左边的阵元（原点）为参考点，假设入射信号方位角为  ，则第  个阵元相对于参考点的时延

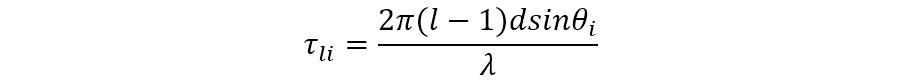
对于以上的数学模型有如下假设：

• 阵列的阵元数  大于信号源数  （保证阵列流型矩阵中各导向矢量的线性独立性），快拍数  大于阵元数（保证统计性能的有效性）

• 不同的快拍数之间的噪声协方差矩阵为  ，也就是不相关，且各阵元接收的噪声是正态分布的，噪声功率为  

• 信号协方差矩阵  是正定的（非奇异）

上述的假设意味着数学模型中的加性噪声为空间白噪声。下面讨论基于上述假设的最大似然准则。

确定性最大似然（SML）

在确定性最大似然的数据模型中，背景噪声和接收噪声被认为是大量独立的噪声源发射的，因而把噪声过程视为一平稳高斯随机白噪声过程，信号波形则假设是确定性信号，但输入波形是待估计的未知参数（载波频率假定为已知）。

假定空间噪声是白色的和循环对称的。一个复随机过程称为循环对称的，若它的实部和虚部为同一分布，并有一个反对称的互协方差，即  ，且噪声项的二阶矩取为

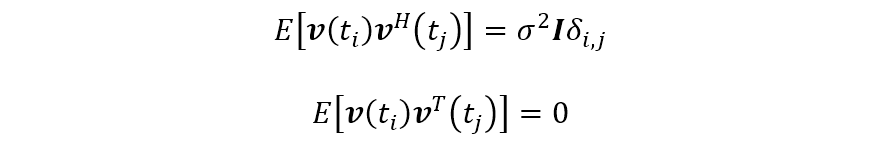
则在上述统计假设下，观测矢量  也是循环对称的，并且是高斯白色随机过程，其均值为  ，协方差矩阵为  。我们知道，似然函数定义为给定未知参数时所有观测值的概率密度函数。

令测量矢量  的概率密度函数是复变量高斯分布，即

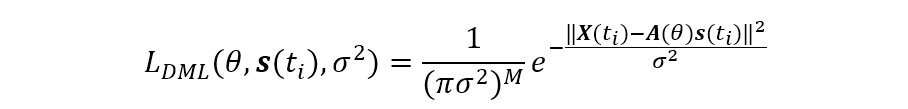
由于测量值是独立的，所以  次快拍的似然函数为

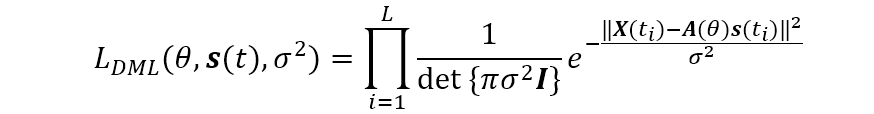
式中：  是复变量的个数（即阵元个数），  表示求行列式的值。  为  维单位阵，  为阵元噪声功率。

如上所述，确定性最大似然法中的似然函数的未知参数是信号参数  和噪声方差  。这些未知量的最大似然估计由似然函数  的最大变化量给出。为了方便，最大似然估计定义为负对数似然函数  的最小化变量。用信号快拍数  归一化，并忽略与未知参数独立的  项，即有

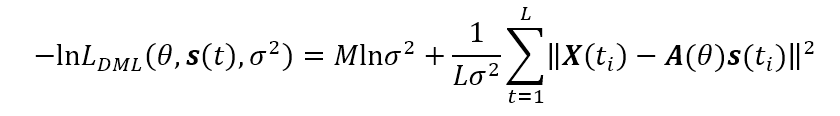
其最小化变量就是确定性最大似然估计值。众所周知，相对于  和  的显式最小化变量为

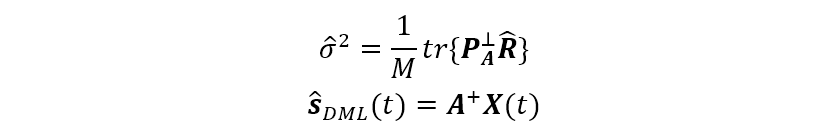
式中：  为  ；  为样本协方差估计，即快拍数据的协方差矩阵；  是  的伪逆矩阵；  是  零空间上的正交投影矩阵，  。

故信号参数  的确定性最大似然估计是下列问题的解:

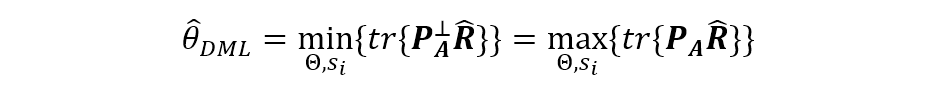
这是因为测量矢量  投影到与所有期望信号分量正交的模型空间上，  在此模型空间的功率测量值为  。显然，当投影把所有真实的信号分量都除去时（即当  时），能量应该为最小。由于只有有限个噪声样本可利用，所以能量不能被准确测量，  将偏离  。

然而，如果是平稳情况，当样本个数趋于无穷大时，误差将收敛为零。这一结果对相关信号甚至相干信号也成立。注意，在单个信源的情况下，  退化为 Bartlett 波束成形器。

为了计算确定性最大似然估计，在数值上必须求解非线性多维优化问题。必要时，还可以求出信号波形和噪声方差的估计值，这只要将  代入  即可。

如果有一个很好的初始值，高斯—牛顿法就能迅速收敛到  的极小值。然而，获得一个足够精确的初始估计值通常是很烦琐的。若初始值差，搜索方法便可能收敛到局部极小值。

随机性最大似然法（SML）

另一种最大似然方法称为随机性最大似然法。在这种方法里，信号波形建模成高斯随机过程。若测量值是利用窄带带通滤波器对宽带信号进行滤波获得的，那么这样一种建模是合理的。

然而，有必要指出，即使数据是非高斯的，这种方法仍然适用。现已证明，信号参数估计的大样本渐进精度只取决于信号波形的二阶性能（功率谱和相关函数）。需要注意的是，高斯信号假设只不过是获得易运用的最大似然法的一种方式。

令信号波形是零均值的，且其二阶特性为

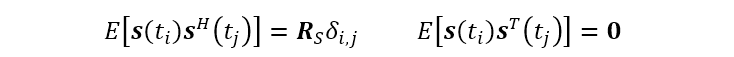
这将使得测量矢量  是一零均值的白色循环对称的高斯随机矢量，其协方差矩阵为

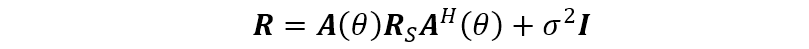
式中，  为信号协方差矩阵。

这种情况下的未知参数组与确定性循环模型的未知参数组不同。现在，似然函数与  、  和  有关，这种情况下测量矢量  的概率密度函数为

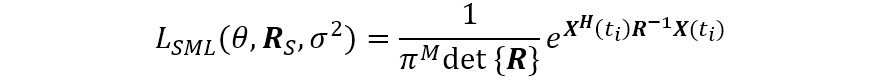
由于测量值是独立的，所以  次快拍的似然函数为

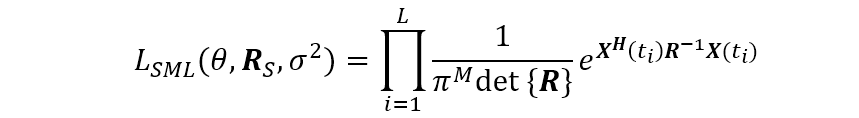
最大似然估计定义为负对数似然函数  的最小化变量。用信号快拍数  归一化，并忽略与未知参数独立的  项，即有

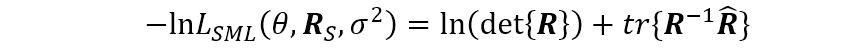
最大似然准则仍使得某些参数是可分离的，对于一个固定的  ，可以证明  和  的随机性最大似然估计分别为

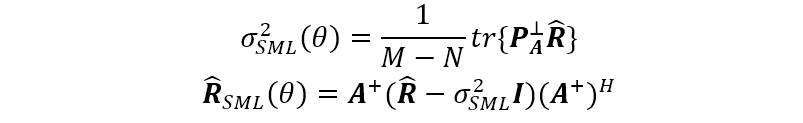
将这两个估计值代入负对数似然函数，则可得到波达方向的随机性最大似然估计，即

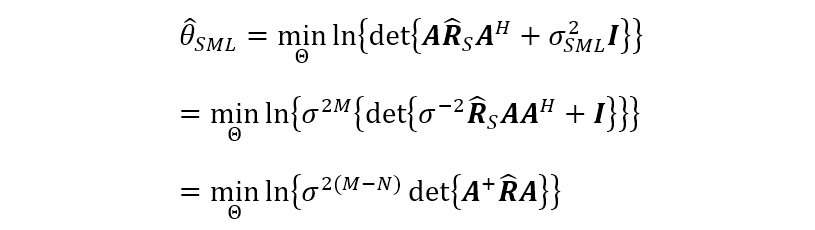
这一准则有一个很好的解释：行列式度量数据矢量的置信区间。因此，我们寻找的观测值模型应该具有“最小成本”，这与最大似然原则是吻合的。

上式的准则函数也是其变量  的非线性函数。由相关资料可知，随机性最大似然法给出的信号参数估计具有比相应的确定性最大似然估计更好的大样本精度。

对于高斯信号，随机性最大似然估计可达到估计误差方差的克拉美—罗下界（CRB），因而随机性最大似然估计是一致估计。与之不同，确定性最大似然估计则不是一致估计，因为它达不到相应的（“确定性的”）CRB。

随机性最大似然优化一般是非常困难的，因为准则数是非凸的。期望最大化（Expectation-Maximization）算法简称 EM 算法，可以用来将的复杂优化 问题转化为一系列二次型优化问题。EM 算法是一种通用的最大似然估计算法。

最大似然算法相关仿真

在  阵元均匀线阵中，阵元间距为信号波长的一半，快拍数为  的场景下，  个信号源分别由  、  、  入射，此时使用最大似然算法对空间谱进行估计，其相关仿真结果如下所示。

下面两图分别对应使用 DML 算法进行估计时极小、极大方法仿真结果。

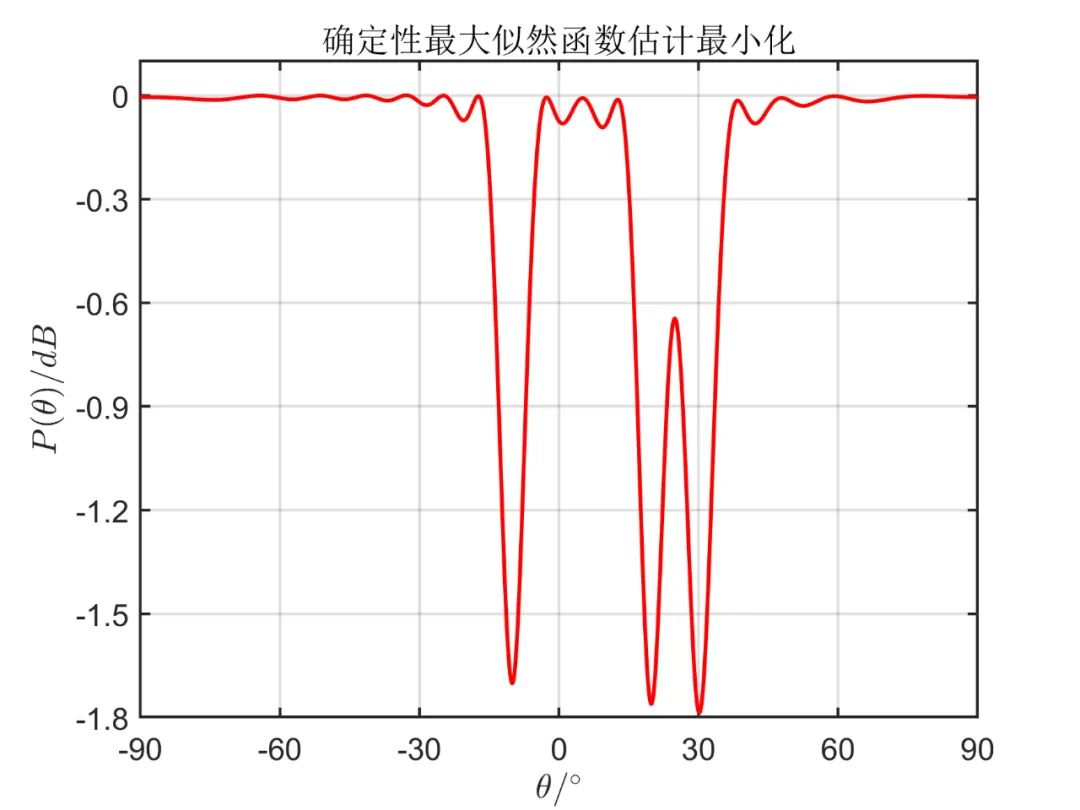
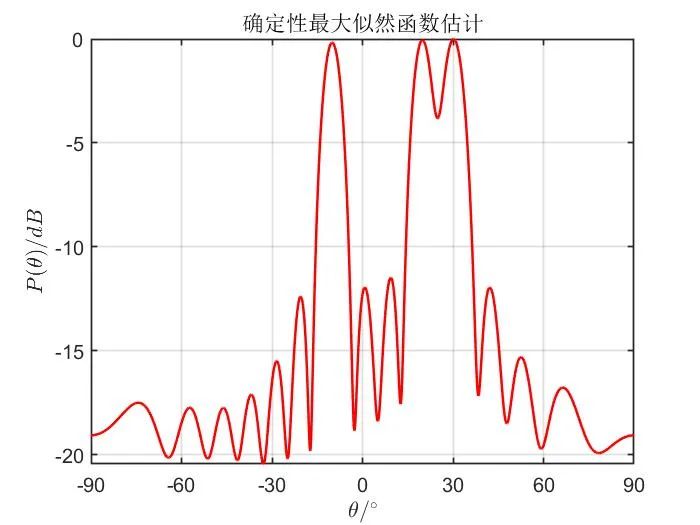
下面两图分别对应使用 SML 算法进行估计的仿真结果，其对应于算法三种表达式。

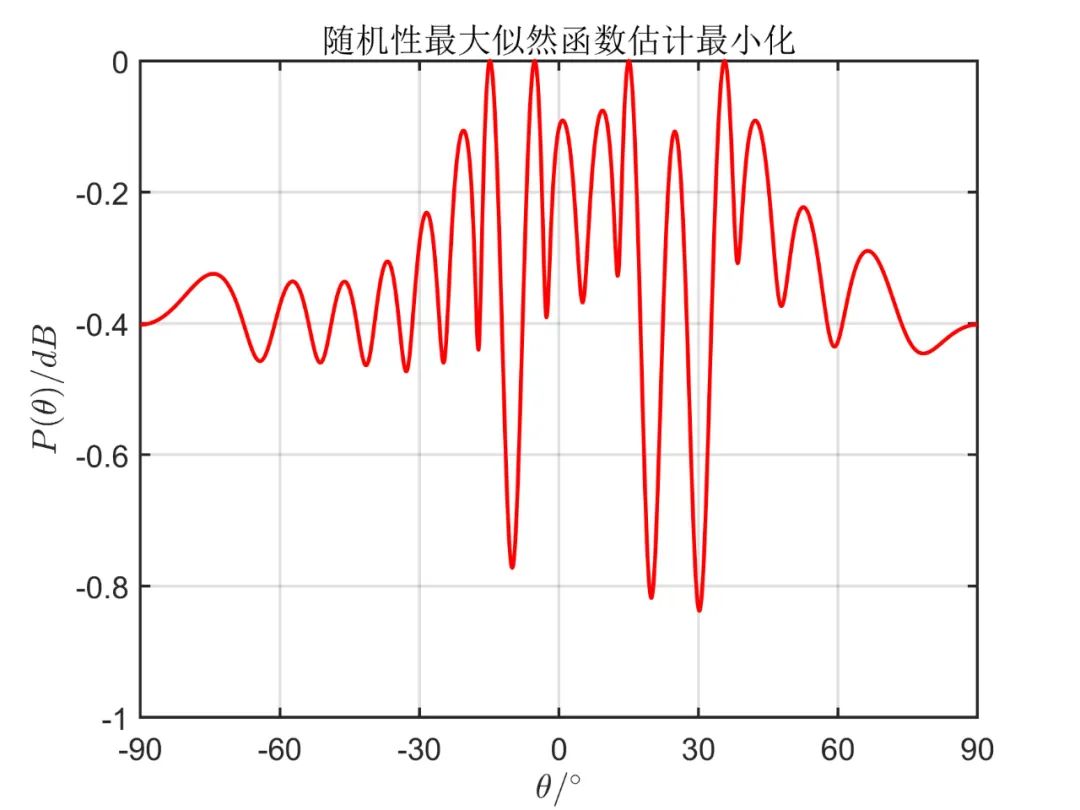
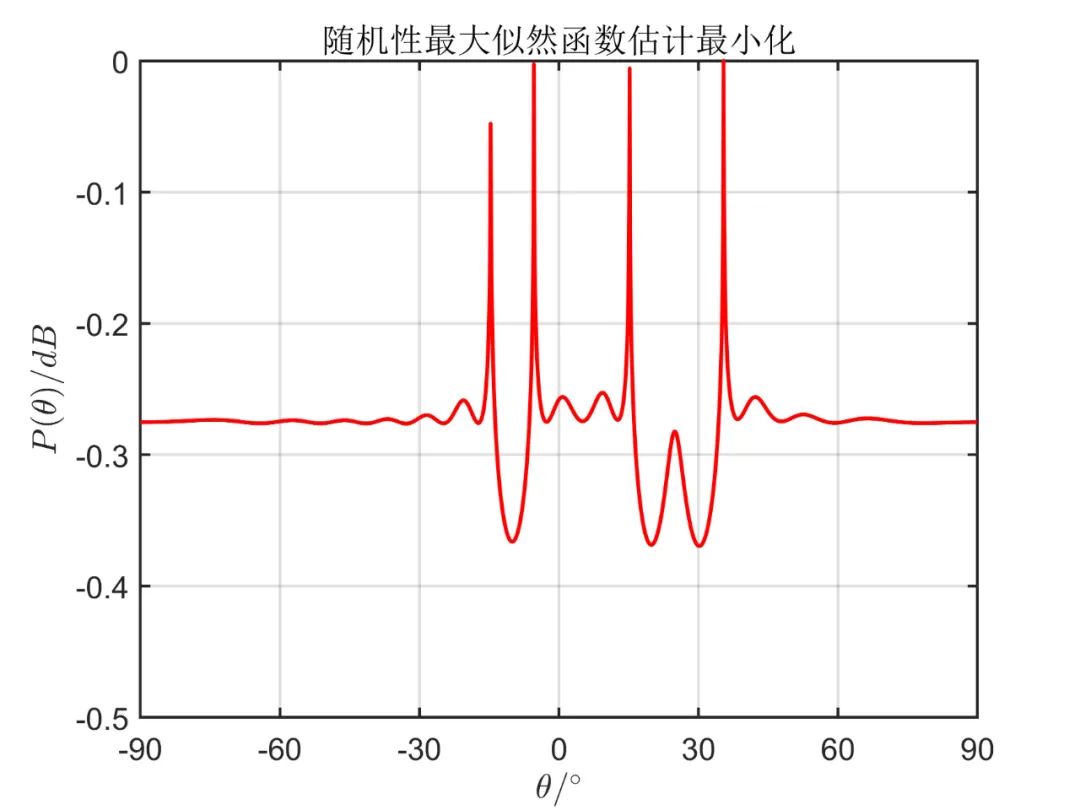
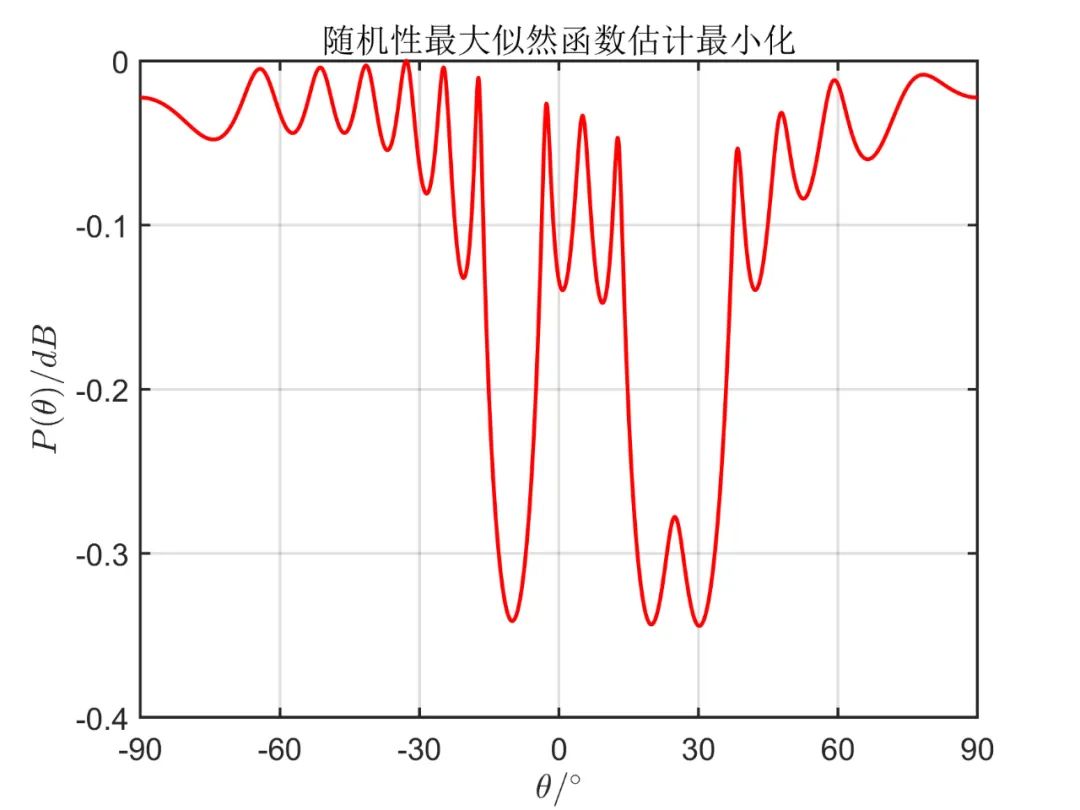
通过相关仿真结果，我们可以清楚的看出，最大似然估计法能准确反映信号空间谱的估计情况，通过谱搜峰搜索其极大、极小值即可确定空间信号的方位角。

－ The End －

版权声明：欢迎转发本号原创内容，转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理，相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请跟我们联系删除。我们致力于保护作者知识产权或作品版权，本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。

投稿/招聘/推广/合作/入群/赞助 请加微信：15881101905，备注关键词

“阅读是一种习惯，分享是一种美德，我们是一群专业、有态度的知识传播者