
来源 | 雷达信号处理matlab
智库 | 云脑智库(CloudBrain-TT)
云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向
声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(15881101905,微信同号)删除,谢谢
在实际环境中相干信号源是普遍存在的,如信号传输过程中的多径现象,或者敌方有意设置的电磁干扰等。相干信号源的检测与估计是空间谱估计中一个重要的研究方向,因此这里介绍一下相干信号源的数学模型。相干信号与非相干信号模型如下图所示。

图源自网络
当考察多个信号时,这些信号之间可以是不相关的、相关的或相干的。对两个平稳信号
由 Schwartz 不等式可知
由前面的讨论可知,MUSIC 算法在理想条件下具有良好的性能,但在信号源相干时算法的性能变得很坏。为什么信号源相干对算法的性能有这么大的影响呢?
当信号源完全相干时,阵列接收的数据协方差矩阵的秩降为
由上面的分析可知:在相干信号源情况下正确估计信号方向(即解相干或去相关)的核心问题是如何通过一系列处理或变换使得信号协方差矩阵的秩得到有效恢复,从而正确估计信号源的方向。目前关于解相干的处理基本有两大类:一类是降维处理;另一类是非降维处理。
降维处理算法
降维处理算法是一类常用的解相干处理方法,可以分为基于空间平滑、基于矩阵重构两类算法。
其中,基于空间平滑的算法主要有前向空间平滑算法、双向空间平滑算法、修正的空间平滑算法及空域滤波法等;基于矩阵重构的算法主要是指矩阵分解算法及矢量奇异值法等。
空间平滑类算法和矩阵重构类算法区别在于矩阵重构类算法修正后的协方差矩阵是长方阵(估计信号子空间与噪声子空间需用奇异值分解),而空间平滑算法修正后的矩阵是方阵(估计信号子空间与噪声子空间可以用特征值分解)。
非降维处理算法
非降维处理算法也是一类重要的解相干处理方法,如频域平滑算法、Toeplitz方法、虚拟阵列变换法等。这类算法与降维算法相比最大的优点在于阵列孔径没有损失,但这类算法往往针对的是特定环境,如宽带信号、非等距阵列、移动阵列等。本期我们将首先讨论空间平滑类算法。
空间平滑算法
众所周知,空间平滑算法是针对一般超分辨算法不能解相干而提出的一种有效方法,它在一般情况下只适合于均匀线阵(ULA)。下面简要介绍空间平滑 MUSIC 利用子阵平滑恢复数据协方差矩阵的原理,然后深入讨论加权空间平滑算法的思想。
空间平滑算法的原理
对于一窄带情况下的均匀线阵,第
空间前向平滑技术的原理如下图所示,将均匀线阵(
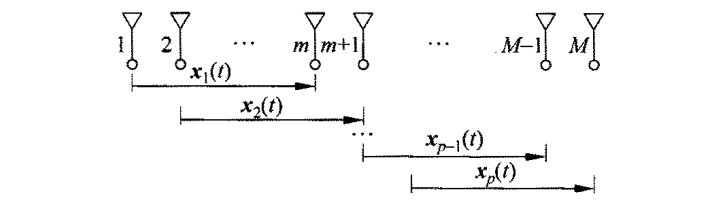
如上图所示,取第一个子阵(一般为最左边子阵)为参考子阵,则对于第
式中,
注:如果子阵阵元数目
如果按下图划分子阵,即采用后向平滑的方法划分子阵。
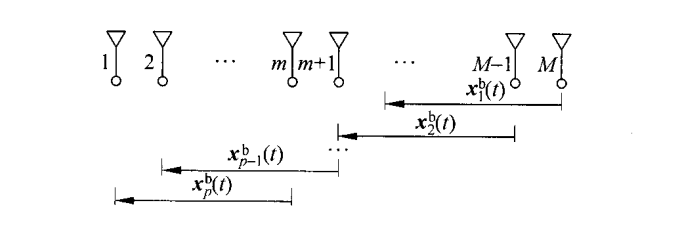
则第
所以后向平滑第
如果子阵阵元数目
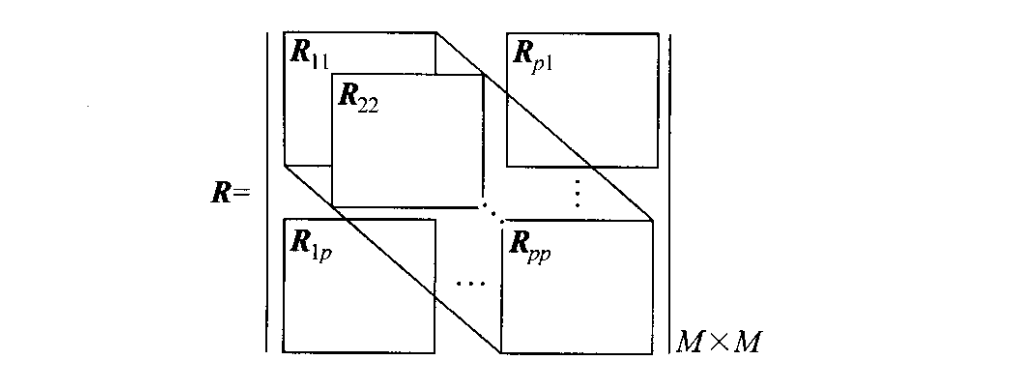
上面是从各子阵的数据协方差矩阵角度出发得出的结论,下面换一个角度来考虑上述的空间平滑算法。定义如下两个
通过上面的定义发现前向平滑及后向平滑的子阵数据模型可以分别变为以下两式:
仔细分析以上两式。考虑前后向空间平滑算法中的第
前向平滑的第
从上述分析中可知,前后向空间平滑算法只利用了
加权空间平滑算法
通过上面的讨论,可以发现常规的空间平滑算法的原理就是利用原始数据协方差矩阵的各对角子阵信息(子阵的自相关信息)实现解相干,没有利用各子阵间的互相关信息。很显然,对于大阵列小子阵阵元数的情况,整个数据矩阵的信息会有很大的损失,不可避免导致算法性能的下降。
为此,提出一种充分利用阵列所有子阵的互相关及自相关信息的方法加权空间平滑算法。下面详细分析这一算法,该算法的协方差矩阵由下式构成:
式中,
该式可以看成是空间平滑算法的统一框架,不同的前后向加权矩阵可以得到不同的空间平滑算法。下面列举加权空间平滑算法的几个特例。
(1)当前向平滑权矩阵
(2)当前向平滑权矩阵
(3)当前向平滑权矩阵
该式即是修正的空间平滑(MSS)算法,通常也称为双向平滑算法,其实质就是前向平滑修正矩阵式与后向平滑修正矩阵式的平均。
对于双向空间平滑算法,如果子阵阵元数目
由前面分析可知,单向的空间平滑 MUSIC 算法需要有
事实上,当有
空间平滑的 MUSIC 算法及其仿真分析
通过上面的分析可知,空间平滑的 MUSIC 算法之间的不同点在于得到修正协方差矩阵的方法不同,但它们的目的都是为了通过空间平滑处理实现解相干。
下面,我们总结基于空间平滑的 MUSIC 算法的计算过程。
由阵列的接收数据得到数据协方差矩阵
利用上述介绍的方法对
利用修正的协方差矩阵进行 MUSIC 谱估计,找出极大值对应的信号方向
空间平滑算法的实质是对数据协方差矩阵的秩进行恢复的过程,但这个过程通常只适用于等距均匀线阵,而且修正后矩阵的维数小于原矩阵的维数,也就是说解相干性能是通过降低自由度换取的。
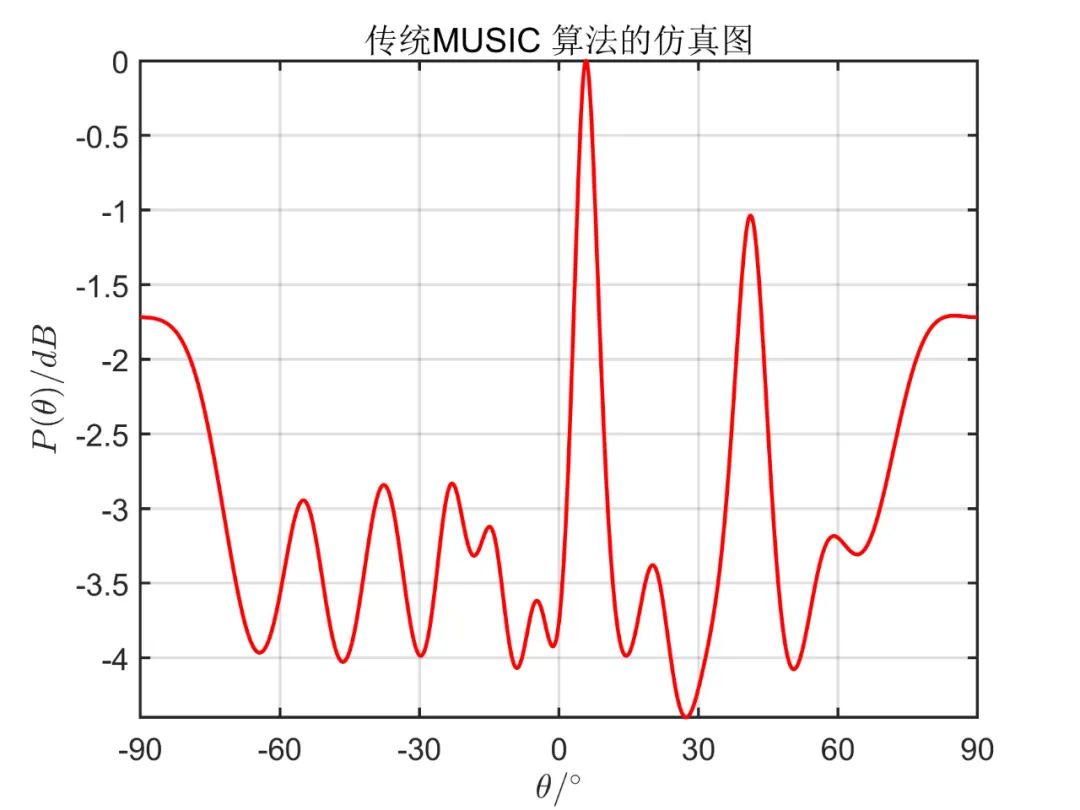
下面为在
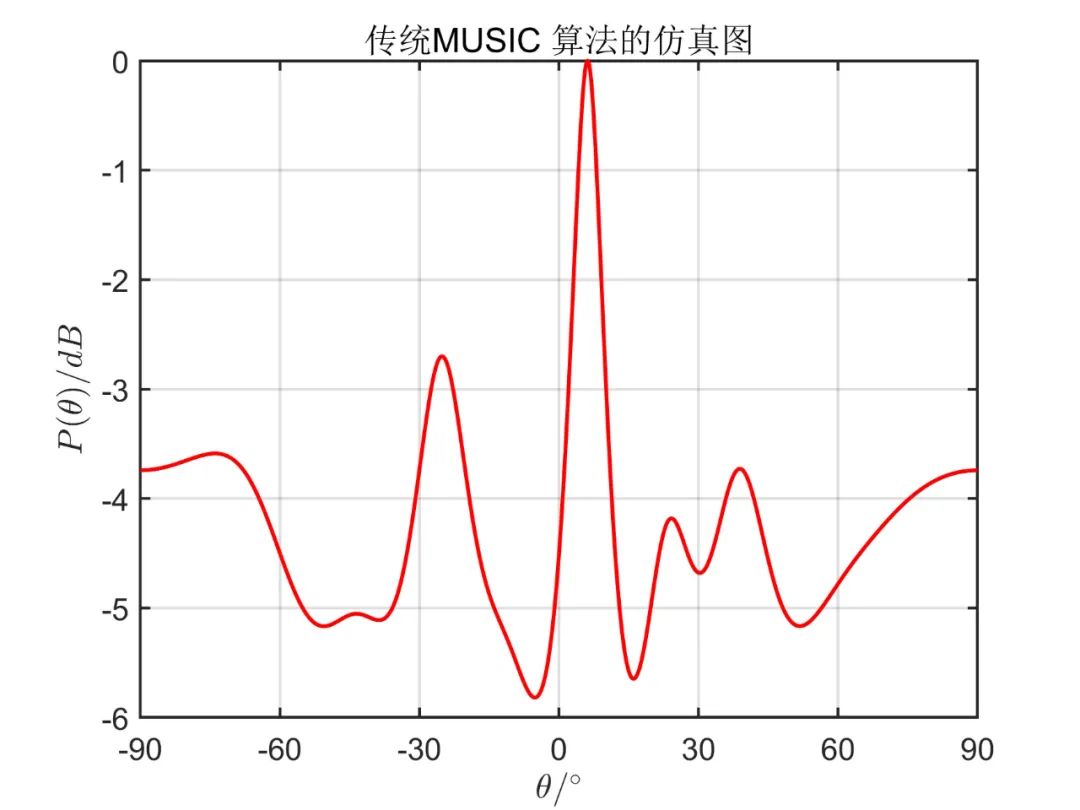
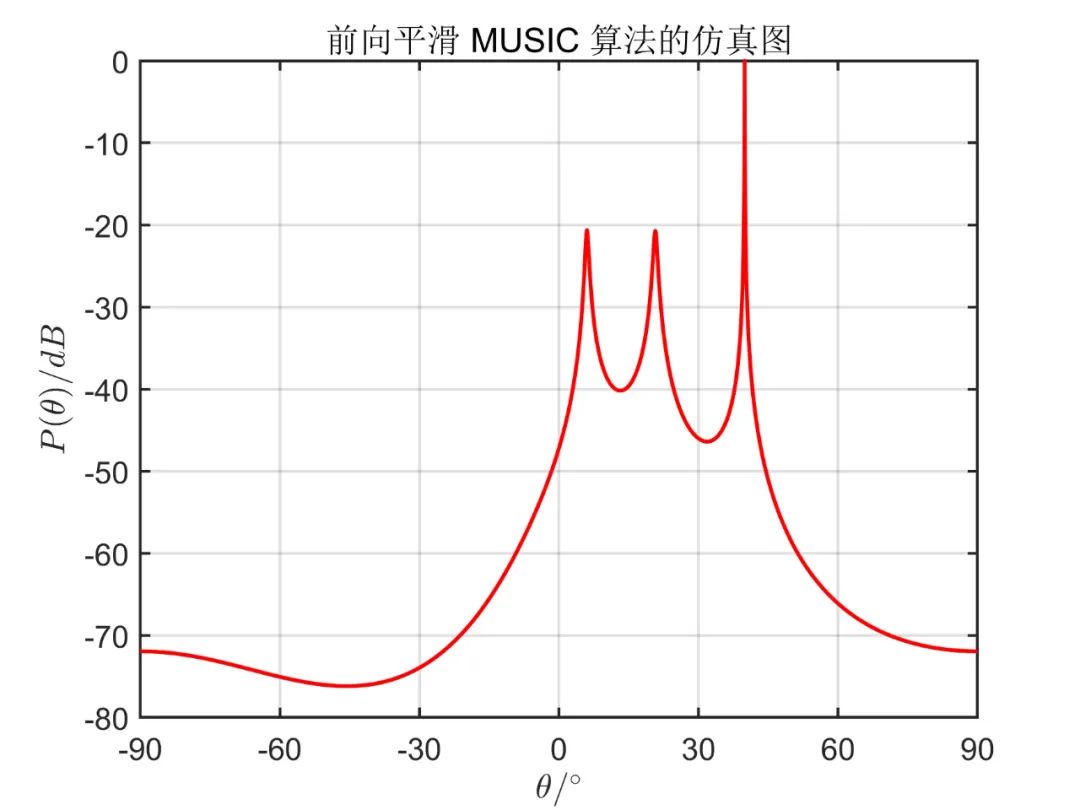
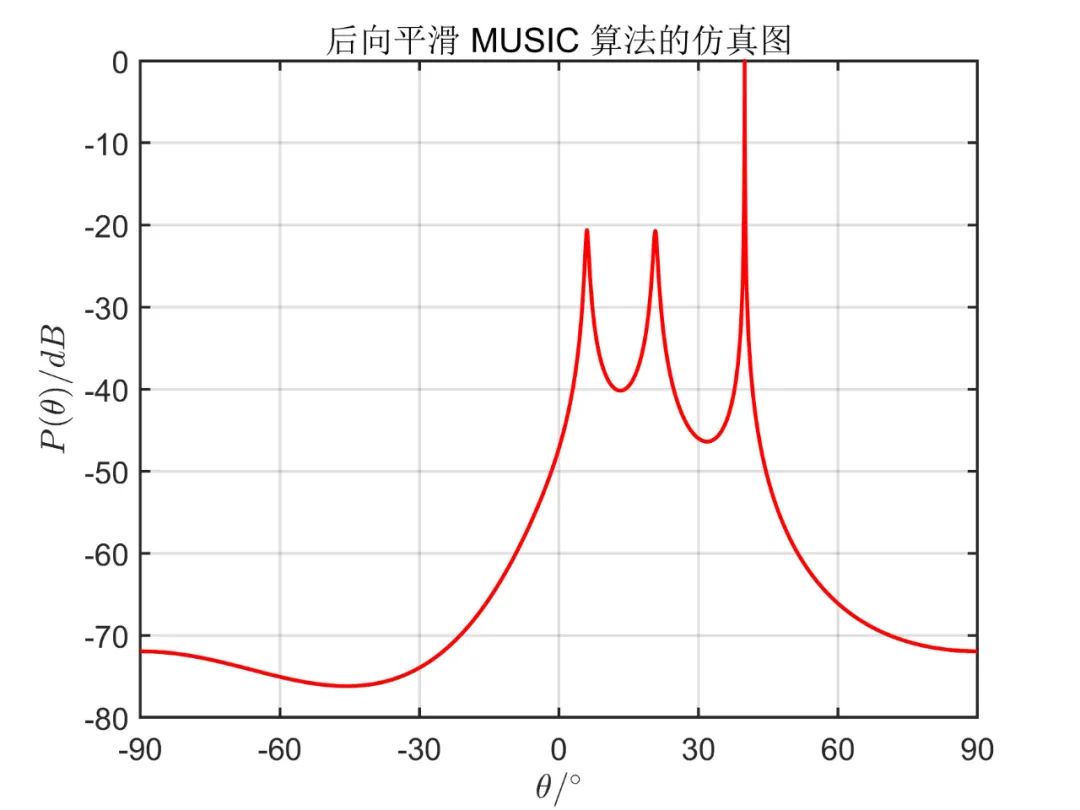
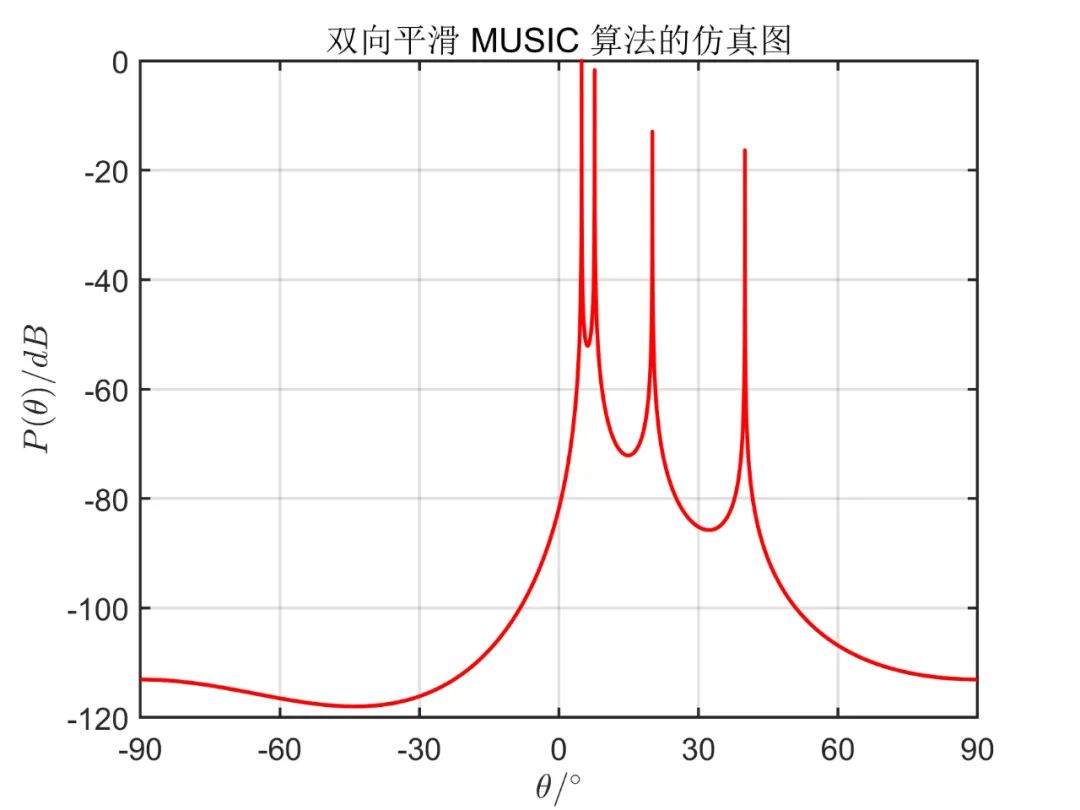
从仿真效果中可以看出,传统 MUSIC 算法无法正确估计相干信号源方向,而空间平滑算法能准确估计出相干信号源方向,且从仿真效果可以看出,双向平滑算法(MSS)分辨率要明显好于前后向平滑算法(SS)。
本文理论部分参考自《空间谱估计理论与算法》。
在上期我们介绍了降维处理解相干可分为空间平滑和矩阵重构两类算法。
矩阵重构类算法
下面讨论矩阵重构类算法,矩阵重构类算法主要分为三类:一是矢量奇异值法;二是矩阵分解算法;三是 Toeplitz 类算法。
矢量奇异值法(SVD)
对数据协方差矩阵进行分解可以分别得到由信号特征矢量组成的信号子空间及由噪声特征矢量组成的噪声子空间,且信号源完全不相关时,信号子空间的维数等于信号源数,而当信号源相干时,信号子空间的维数会减少。那么这个信号特征矢量与导向矢量之间有什么关系?
假设
由上述分析可知,当噪声协方差矩阵为理想白噪声时,上式可简化为
上式组成的协方差矩阵可以表示为如下形式
上述定理提供了一种有效的解相干算法——特征矢量奇异值法(ESVD)。另外需注意,将矩阵
由上述说明可以看出,矢量奇异值算法的共同点在于找出一个矢量,这个矢量要包含所有的信号信息,这样在重构的数据阵中就可估计出相干信号源的信号或噪声子空间。
基于矢量奇异值算法的 MUSIC 计算过程如下所示。
通过预处理得到一个数据矢量
利用数据矢量重构矩阵
利用 MUSIC 算法进行 DOA 估计
关于基于矢量奇异值算法的 MUSIC,作如下进一步说明:
矢量重构算法与空间平滑算法相似,解相干的性能都是通过降低自由度获得的
数据重构矩阵
这类算法一般只适用于均匀线阵
下面为在
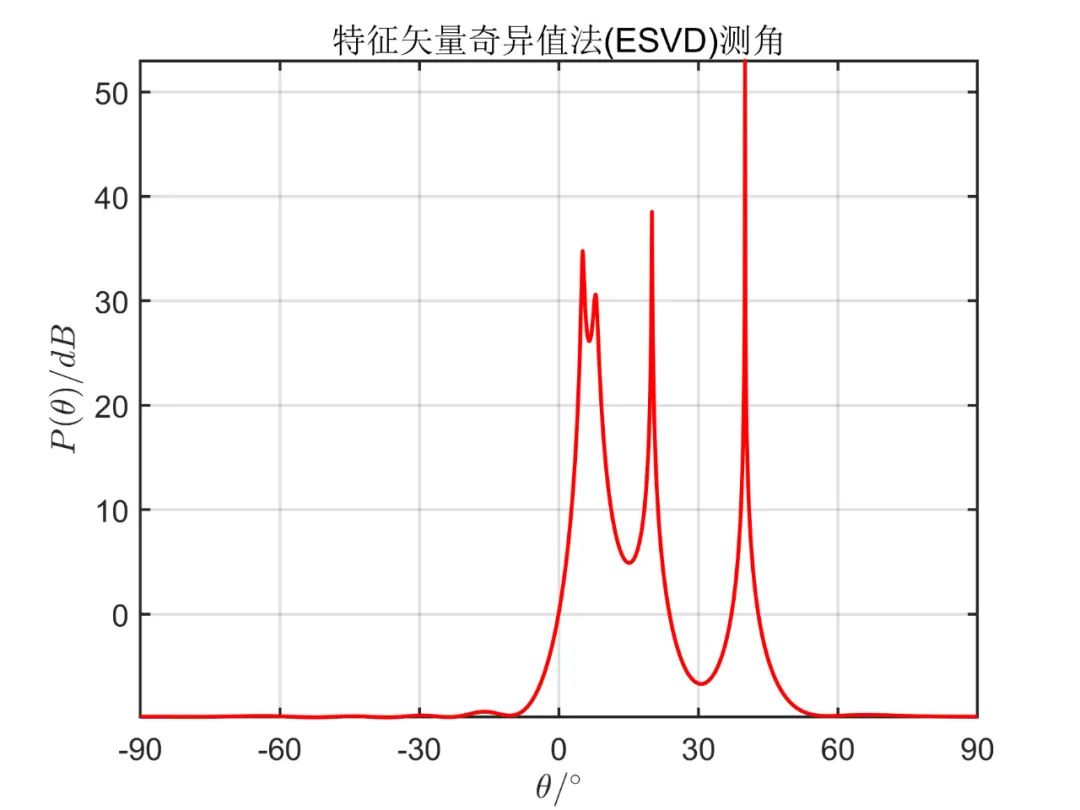
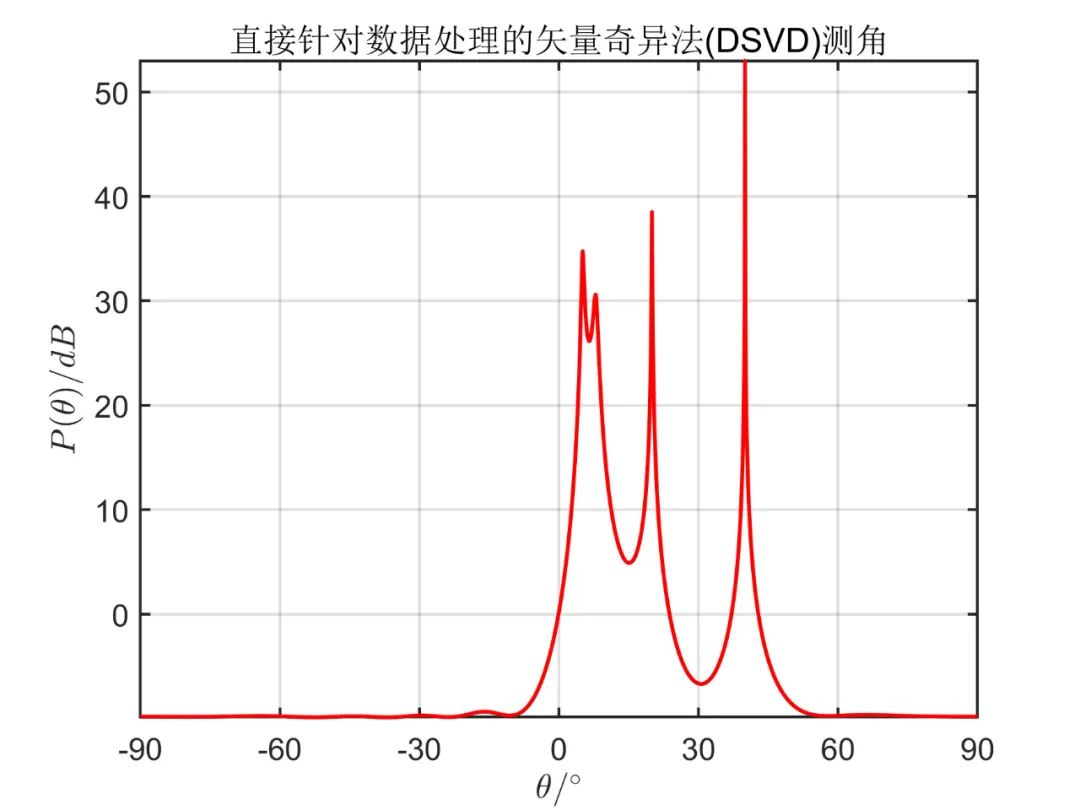
从仿真效果中可以看出,传统 MUSIC 算法无法正确估计相干信号源方向,而 SVD 算法能准确估计出相干信号源方向。
矩阵分解算法
矩阵分解算法也是一类矩阵重构的算法,但它的重构与上述的奇异矢量法不同。
设
若
显然上式所示的 MD 算法是针对理想情况下的矩阵重构,与空间平滑技术相似,为了提高解相干的性能,可以在修正矩阵中添加反向平滑项,即得 MMD 算法的修正矩阵
另外,我们也提出了一种减小计算量的修正的矩阵分解算法,其思想是将空间平滑技术应用到矩阵分解中,称之为 SMD 算法。从前面空间平滑的技术中可知,前向平滑后的修正矩阵为
根据以上的理论分析,将基于矩阵分解的解相干算法归纳为下面所述的步骤。
对阵列的数据协方差矩阵进行重构
对重构的矩阵进行奇异值分解,得到数据的信号子空间与噪声子空间
利用 MUSIC 算法进行 DOA 估计
对于基于矩阵分解的解相干算法,还应注意以下几点:
矩阵分解算法、矢量重构算法与空间平滑算法相似,解相干的性能都是通过降低自由度获得的
数据重构矩阵
当相干源数多时,SVD 算法的运算量要小很多
相同条件下 MMD 算法的仿真如下所示。
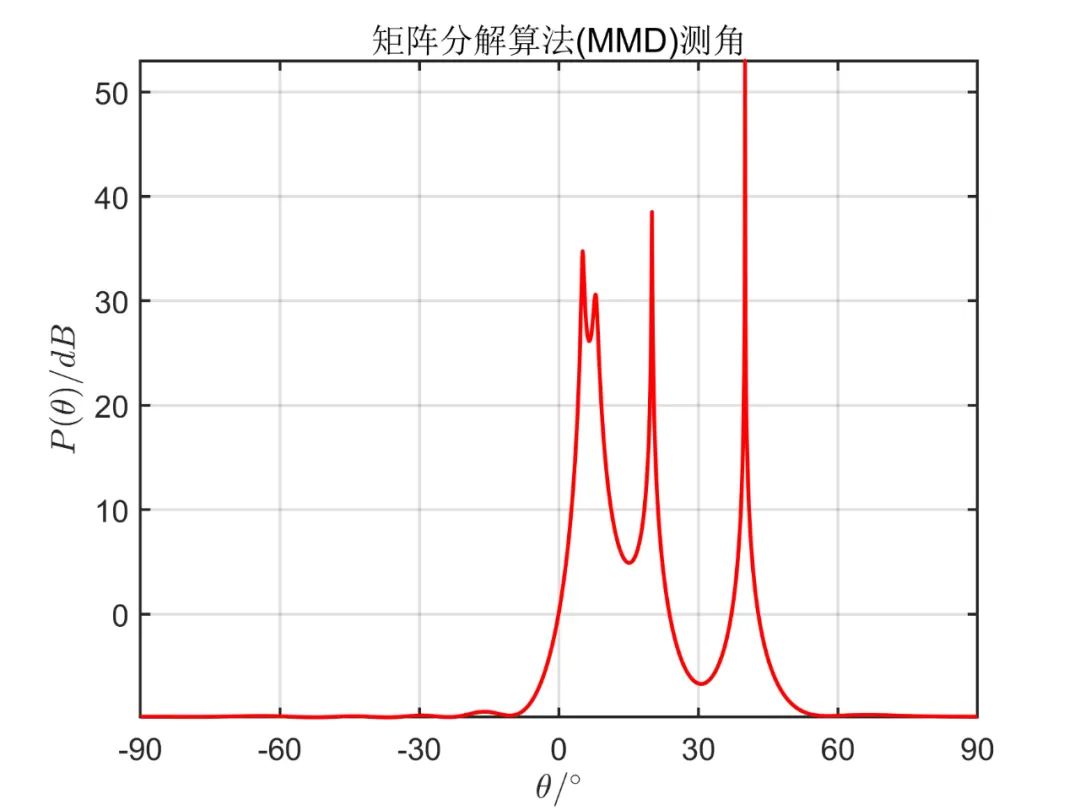
前面讨论的 MUSIC 及相关应用场合的算法都是建立在阵元空间基础上的,即每个阵元都对应于一个数据处理的通道。这一节讨论波束空间的 MUSIC 处理。所谓的波束空间是指先将空间阵元通过变换合成一个或几个波束,再利用合成的波束数据进行 DOA 估计,其原理如下图所示。
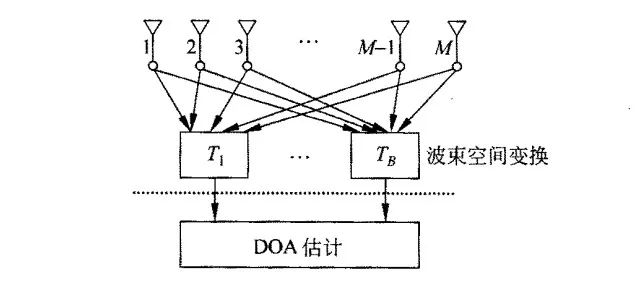
从图中可知,波束空间处理需要通过阵元合成一定数量波束通道作为数据接收通道,这和阵元空间处理中每个阵元对应于一个接收通道完全不同。
我们知道,基于特征分解的信号子空间算法的运算量为
显然,波束空间方法在这种场合下能有效降低算法的计算量,如果合成波束的维数
同样,就系统设计而言,数据接收通道的减少可以大大减少系统的复杂性。
波束形成原理及算法
通过前面的知识可知,对于
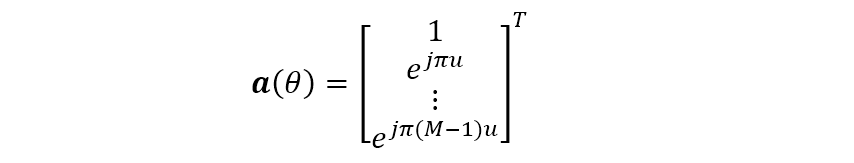
显然,上式可以表示成
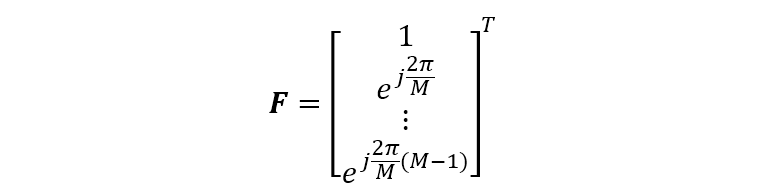
该式表明式阵列的导向矢量也是离散傅里叶变换的一种形式,只是傅里叶变换的因子中
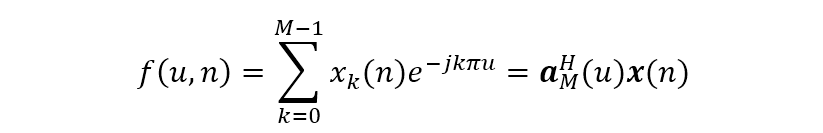
上式表明阵列的导向矢量其实是一个波束形成器,其权值即是
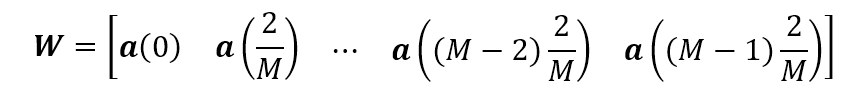
由上面的分析可知,式中每一列表示波束主瓣指向
回到我们的主题,我们的目的是通过阵列的接收数据形成
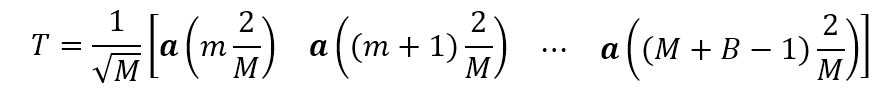
该式就是基于 DFT 波束形成的方法,采用上式的好处在于形成的变换矩阵满足
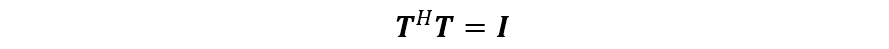
则通过波束空间变换后的输出
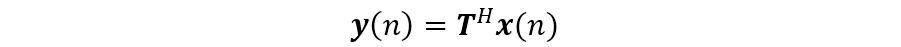
当
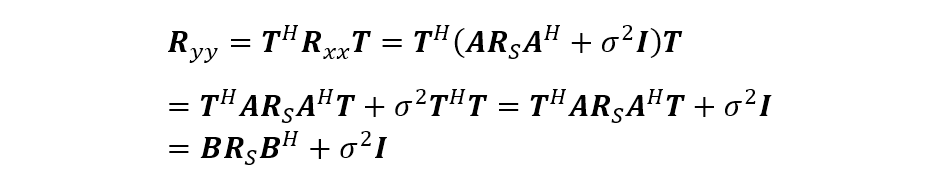
其中,
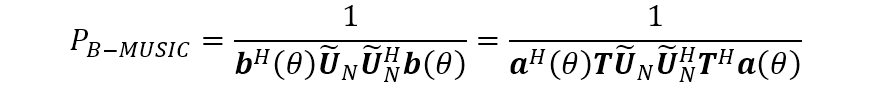
除了上面给出的
(1)设
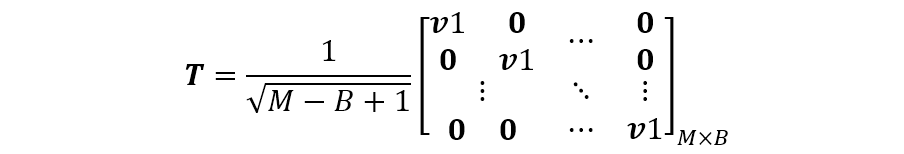
显然,上式不满足
分析上式,不难发现通过波束空间变换后的输出与前节分析的空间平滑的思想相似,即相当于对一个
(2)设
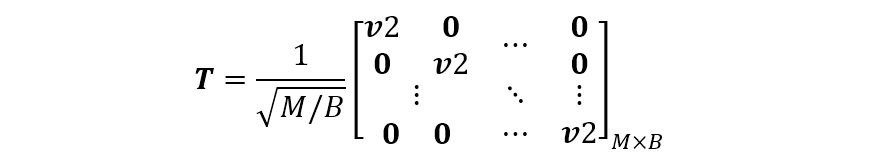
式中的
(3)定义一个
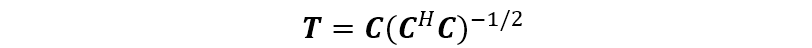
当考察两个相邻信号的分辨力问题时,可以取
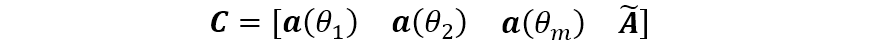
其中,
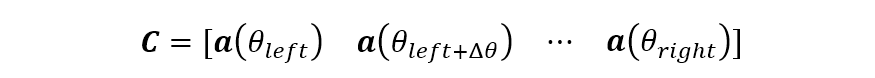
另外
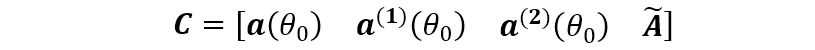
式中,
注意:需要将矩阵
(4)定义如下一个矩阵
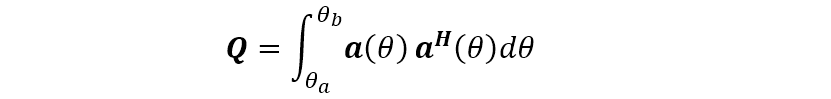
则波束形成矩阵可以取矩阵
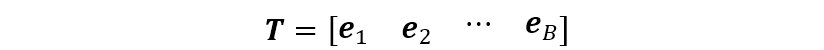
上式也是一种波束形成器。已有文献证明,对于均匀线阵,该波束形成器是最优的。当然当
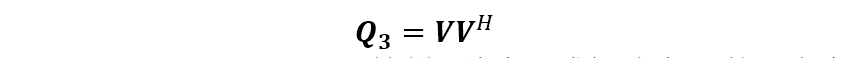
式中,
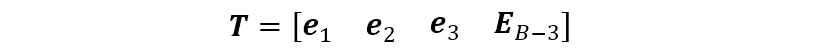
我们将波束空间 MUSIC 算法的计算过程总结于下:
由阵列的接收数据得到数据协方差矩阵
选择不同的波束形成矩阵
利用波束空间的数据矩阵进行 MUSIC 谱估计,找出极大值对应的信号方向
对于波束空间的 MUSIC 算法,需要进一步说明的是:
波束空间的 MUSIC 算法实质就是先将阵列形成几个波束,换言之,就是将阵列接收的数据(阵元空间数据)变换到波束空间的数据,再利用波束空间的数据进行 DOA 估计
波束空间的 MUSIC 算法在利用 MUSIC 算法进行搜索时,注意导向矢量的维数必须等于形成的波束数,而且在对波束空间数据进行特征分解时,矩阵的维数也由原来的阵元数降为波束数
波束空间形成矩阵
相关仿真分析
阵元数目为
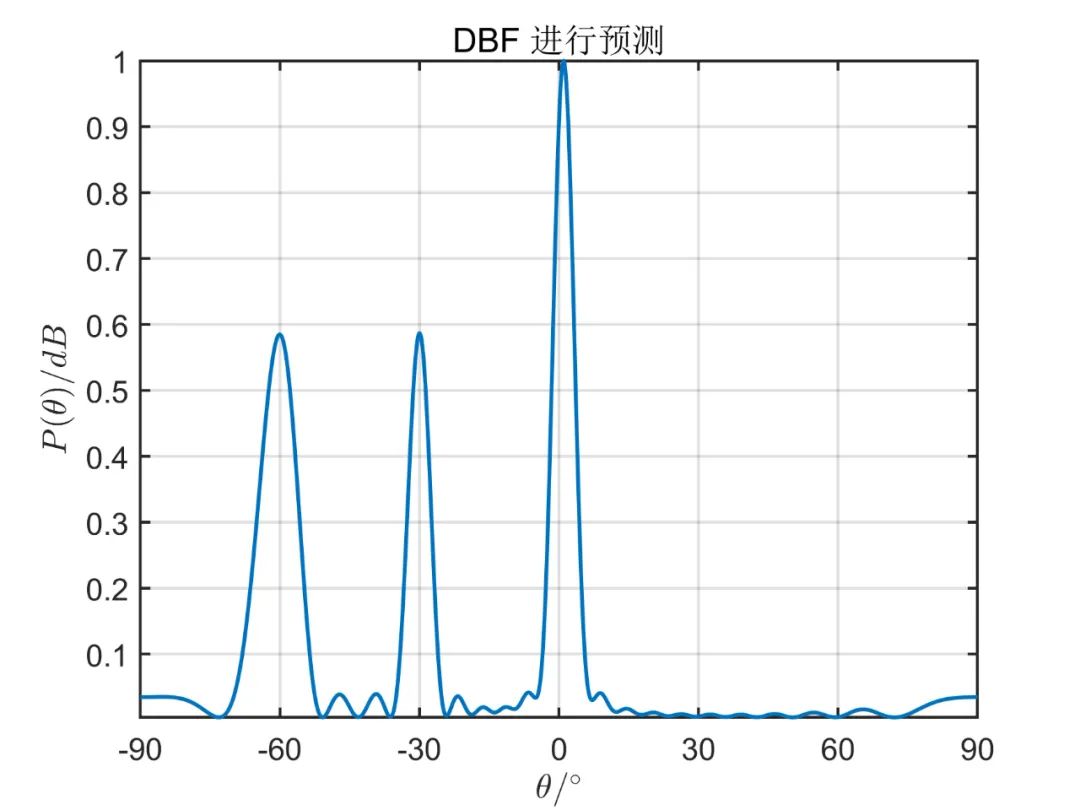
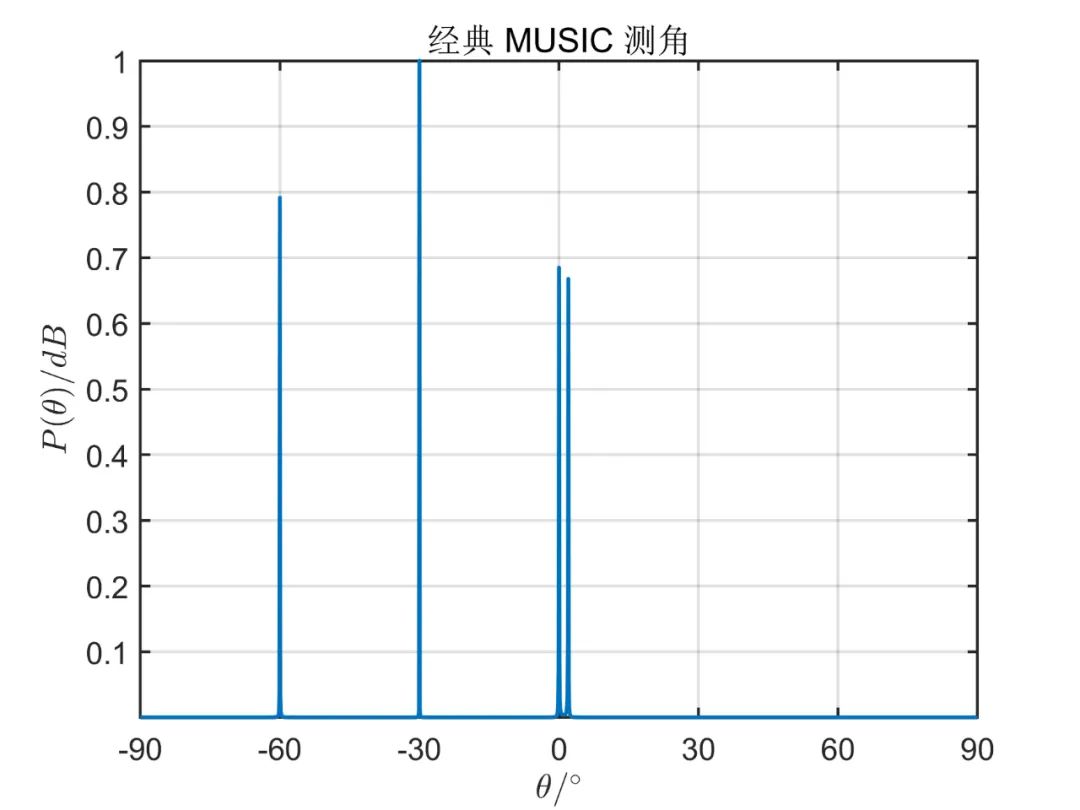
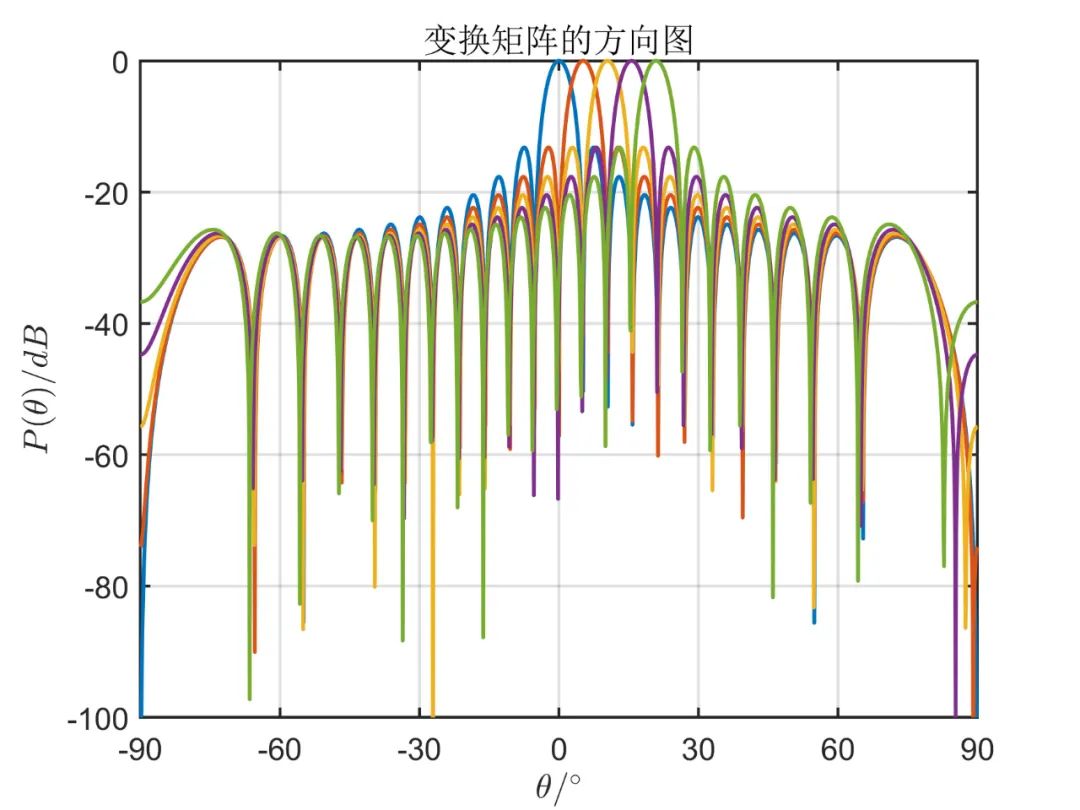
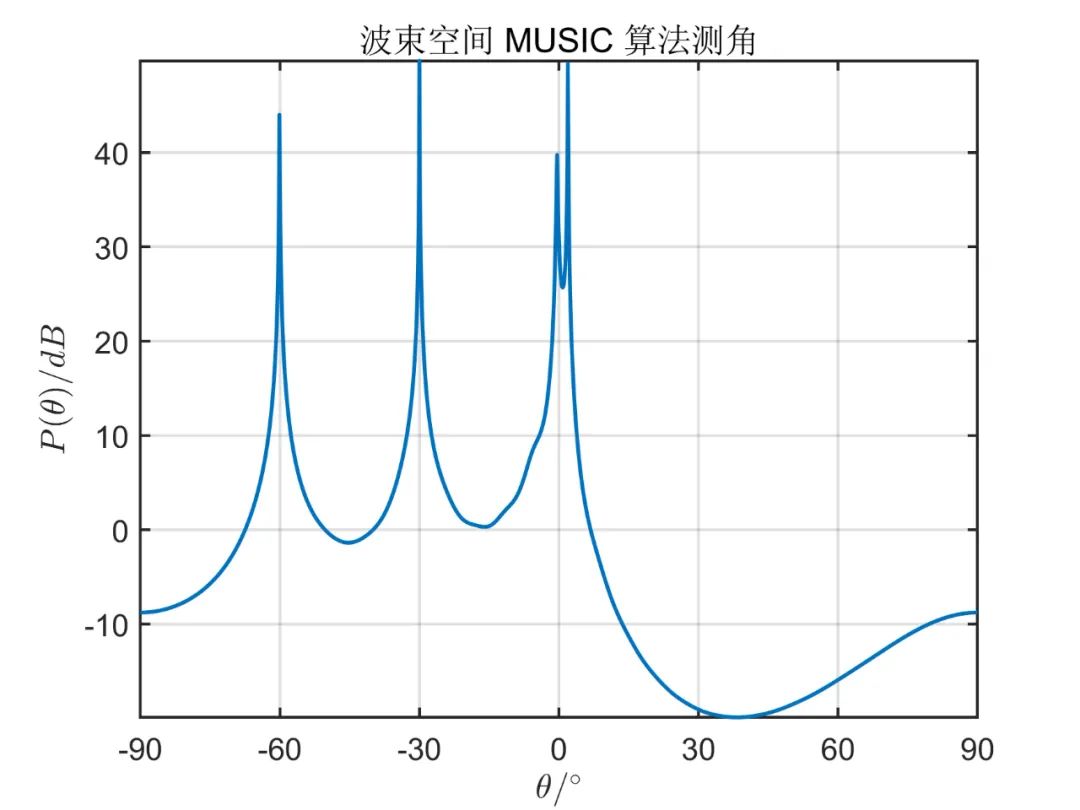
对于相关信号,则只需要把相应的调频率写为
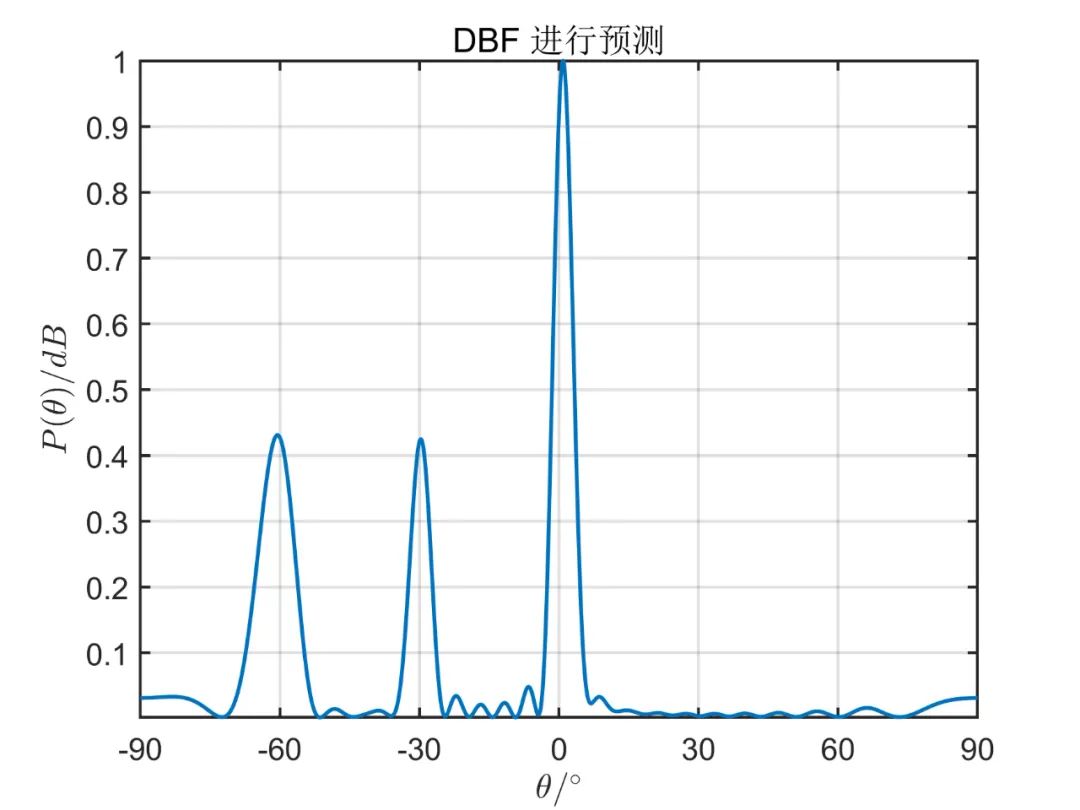
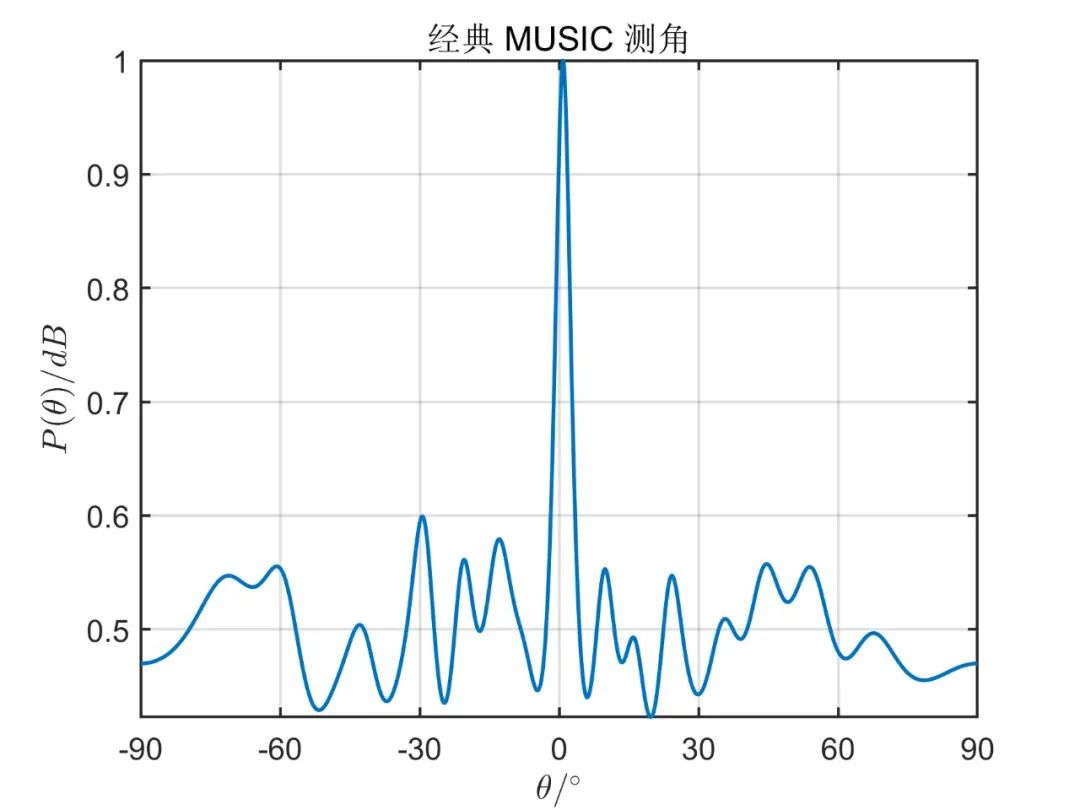

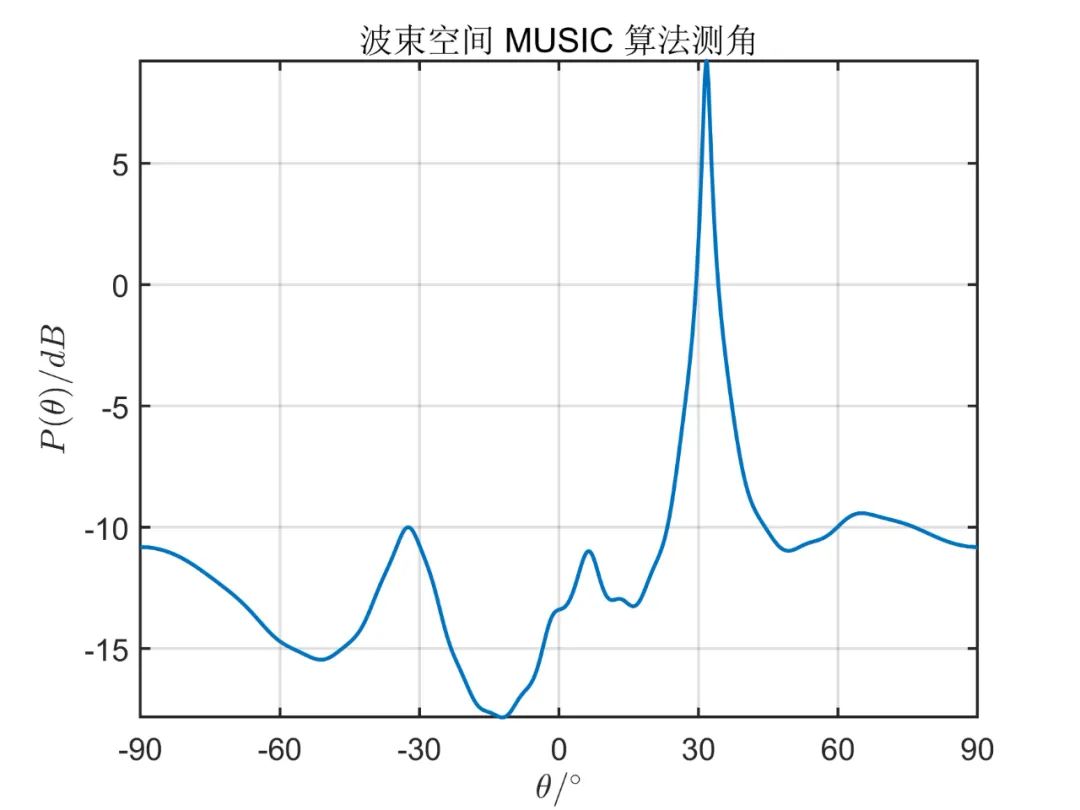
从上面的仿真对比,我们可以得出,一般情况下阵元空间的算法性能优于波束空间,但是使用波束空间算法降低了系统的复杂性,降低了运算量。 由于这种算法因其本质上仍然是 MUSIC 算法,因此对于相干信号,此算法也无法进行解相干。
阵元数目为
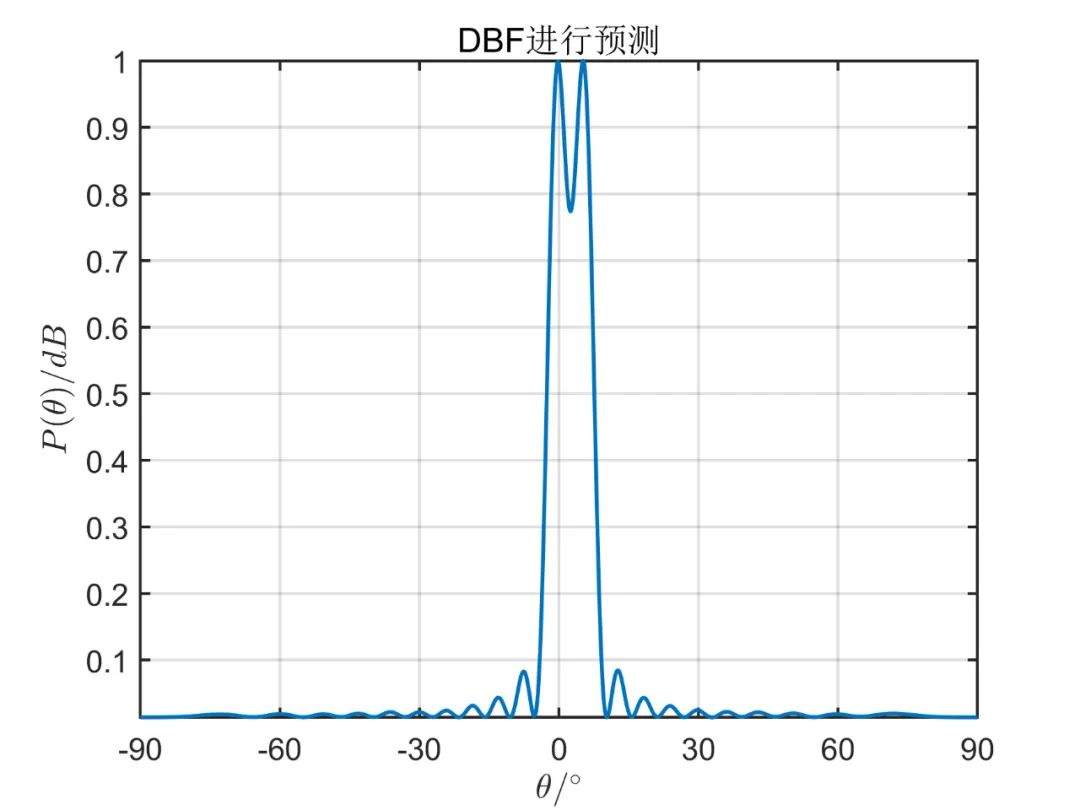
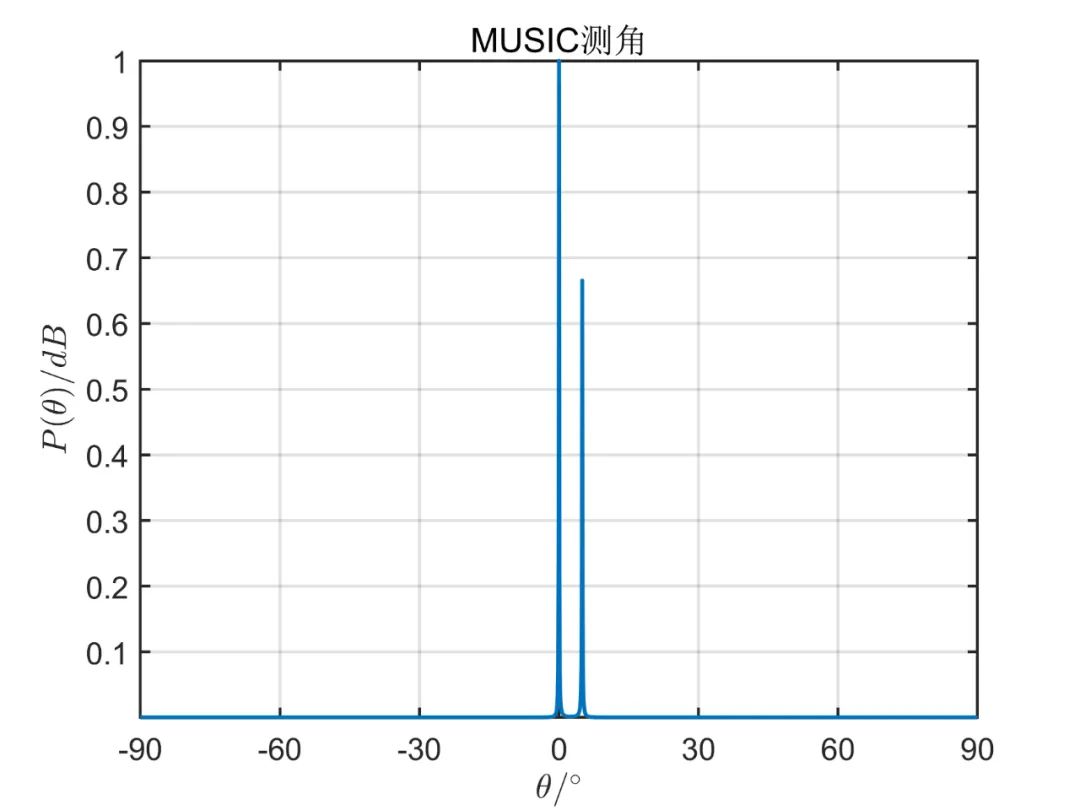
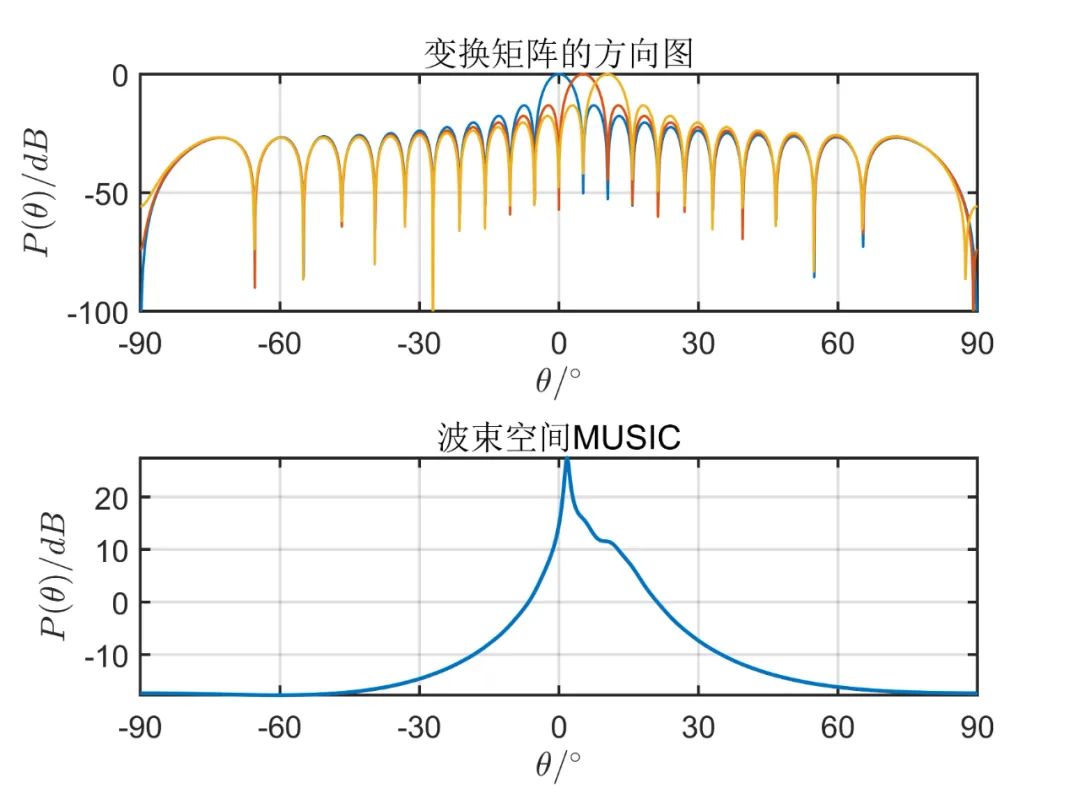
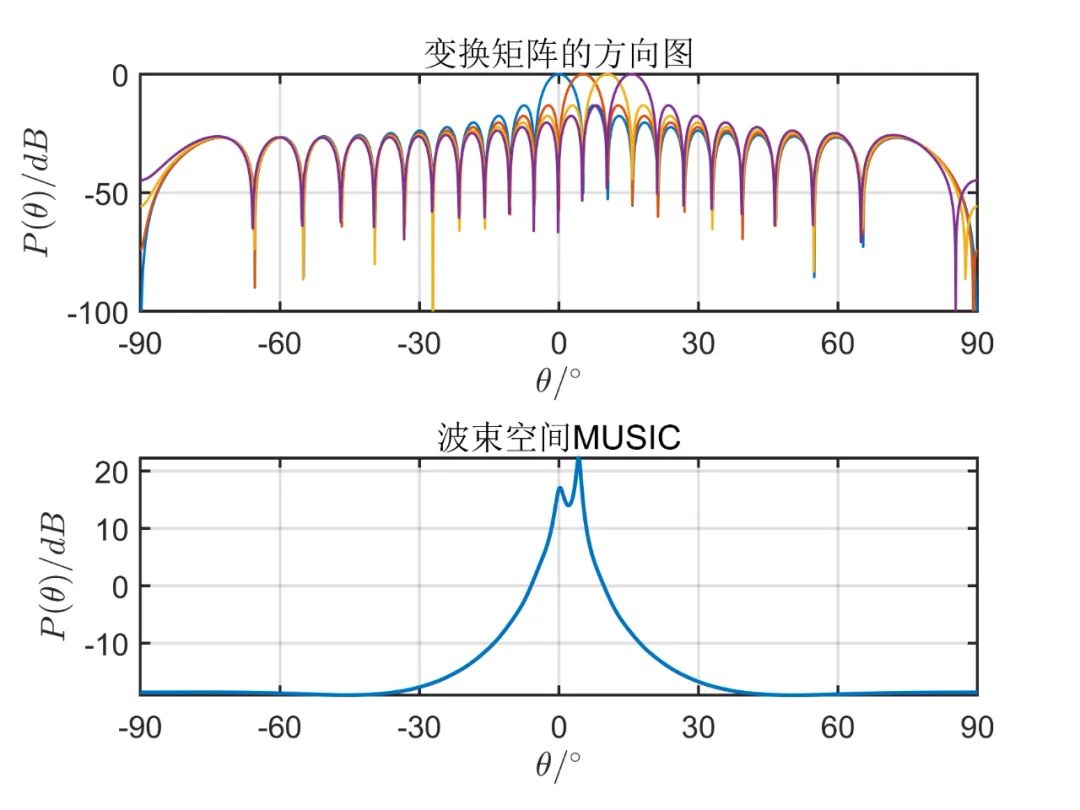
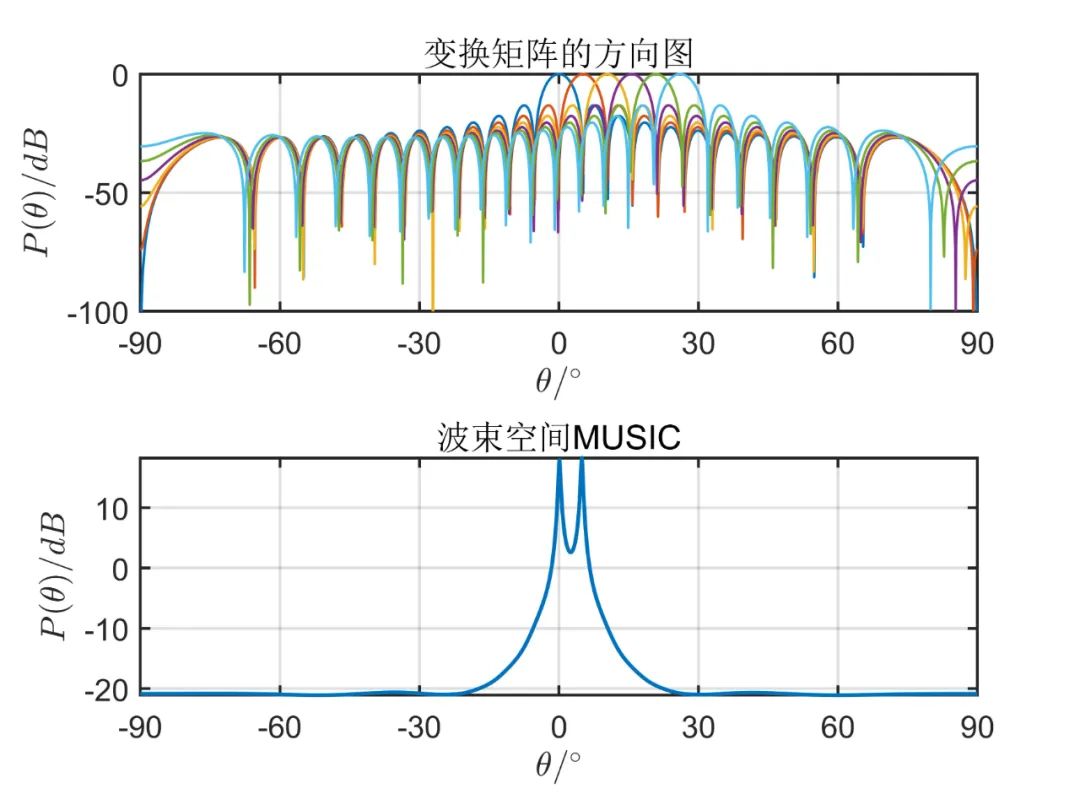
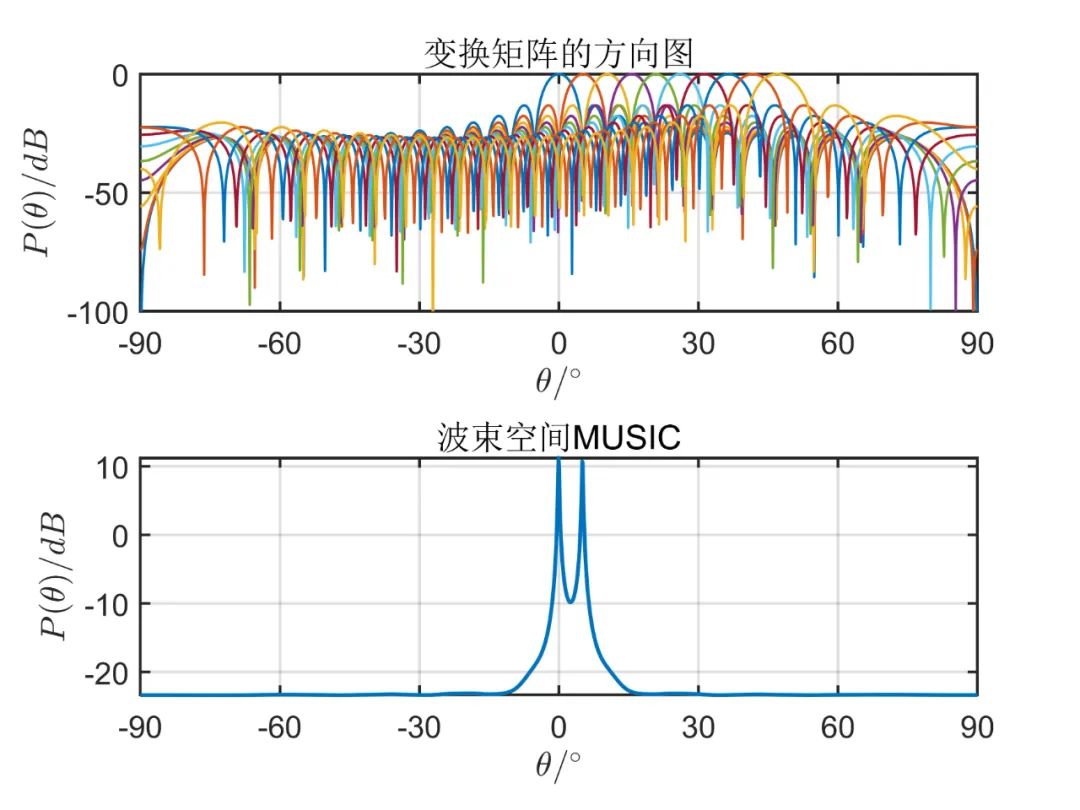
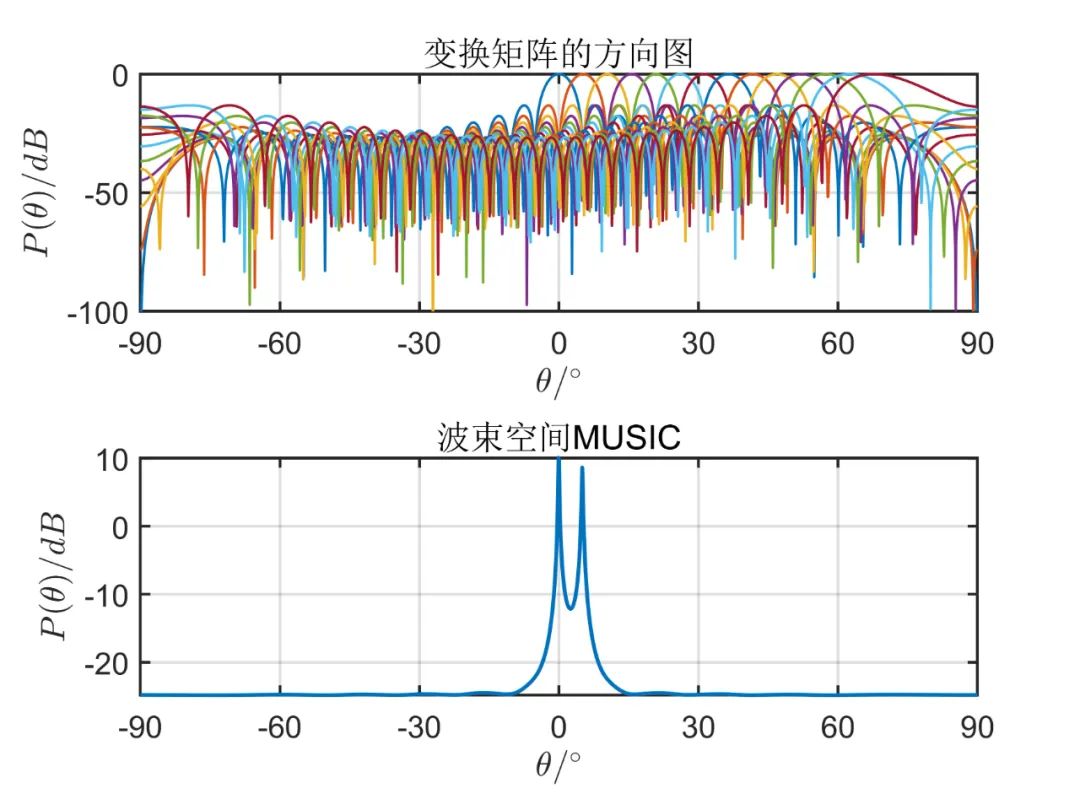
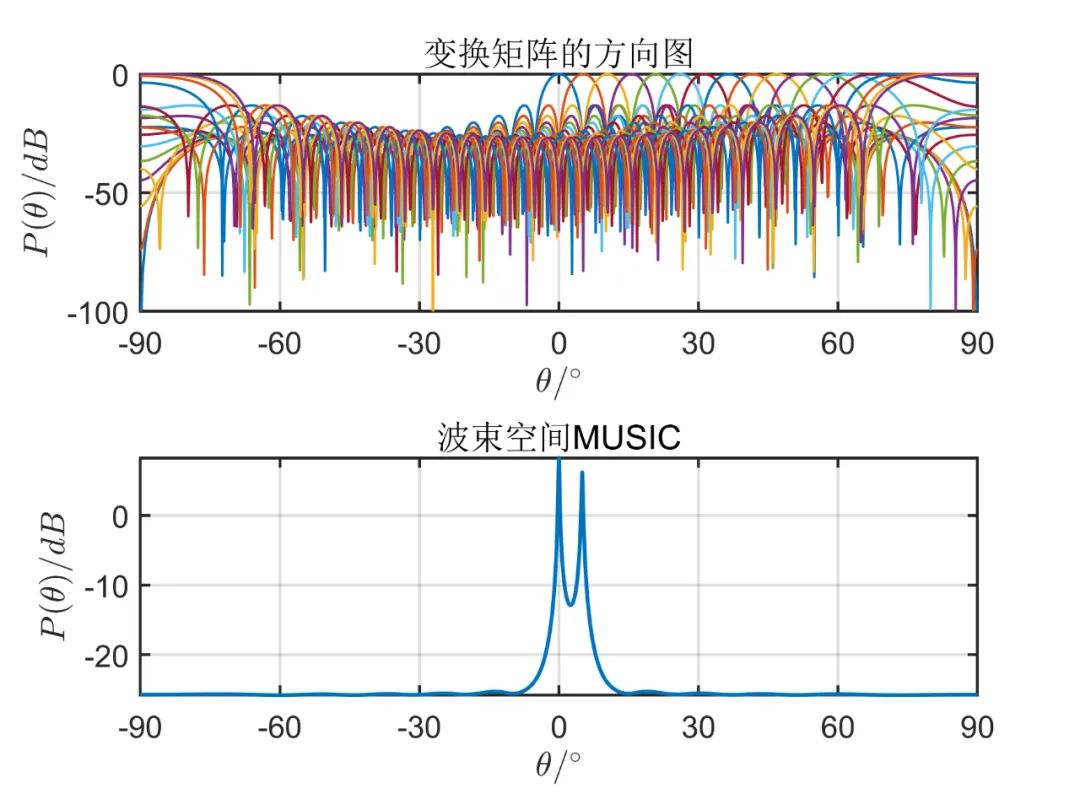
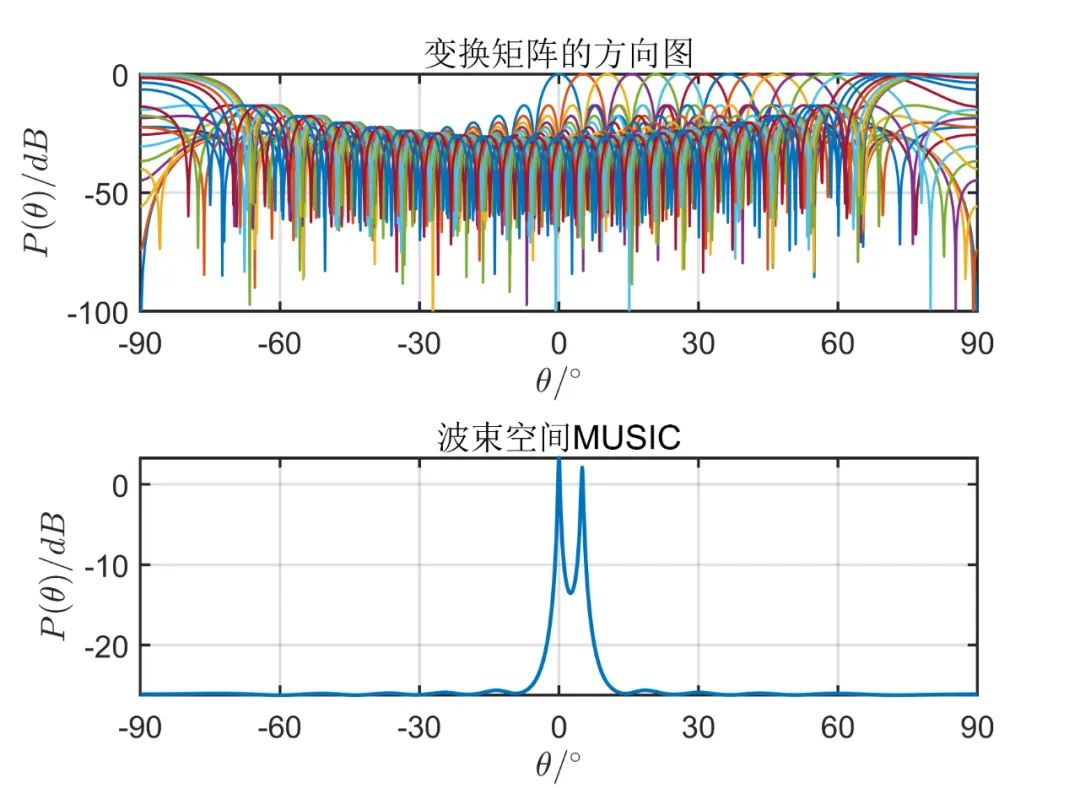
从上述仿真可以看出, 由仿真结果可见,波束空间的数目加大时会有效的改善空间角分辨能力,当波束空间的数目等于阵元数目时,这种算法的性能和常规 MUSIC 算法是一样的;但是波束空间数目增加时又会使计算负担加大,那么这种算法的优点也会消失。
- The End -
版权声明:欢迎转发本号原创内容,转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系删除。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/入群/赞助 请加微信:15881101905,备注关键词

“阅读是一种习惯,分享是一种美德,我们是一群专业、有态度的知识传播者
↓↓↓ 戳“阅读原文”,加入“知识星球”,发现更多精彩内容.
分享💬 点赞👍 在看❤️@以“三连”行动支持优质内容!