
来源 | 大学物理学
智库 | 云脑智库(CloudBrain-TT)
云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向
声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(15881101905,微信同号)删除,谢谢
为帮助正在学习大学物理的同学及时有效的复习和总结,我们整理了全部课程要点以供同学们参考。欢迎分享,谢谢支持!

电荷及其量子性
电荷是自然界中粒子的一种基本属性。电荷有两种,分别称为正电荷和负电荷。自然界的粒子所带的电荷不能无限小,一个基本的电荷量是指电子所带的电量,数量为
根据电荷间作用的规律,即“同种电荷相互排斥,异种电荷相互吸引”,可以确定电荷的种类是两种。电荷是粒子的属性,同质量一样,电荷也具有相对论不变性,不同的是,它还满足电荷守恒定律。
点电荷
点电荷是指大小和形状可以忽略,可以看成一个点的带电体。同质点一样,是否能被看作点电荷,也依具体问题而定。
库仑定律
同种电荷相互排斥,异种电荷相互吸引。真空中,两个点电荷之间的相互作用力沿着二者连线的方向,按照如下公式给出
理解库伦定律矢量式的含义,当考虑电荷1对电荷2的作用时, 从1指向2,否则 就反向。无论电荷1和2的电性如何,只要规定正电荷用正数,负电荷用负数,库仑力的方向总能自动通过矢量式获得。
试验电荷
为了尽量减少因为电场力过大,而导致场源电荷重新分布,进而影响空间电场的分布,基于点电荷的模型,定义所谓“试验电荷”,即带电量足够小的点电荷。
电场与电场强度
与超距作用观点不同,场的观点认为作用是通过场有限速度来传递的。电场就是传递电荷相互作用的媒介。
试验电荷在空间某点所受到的电场力与试验电荷的量的比值描述该点的电场的强弱,称之为电场强度,其方向与该点正电荷受力方向一致,即
电场的叠加原理
根据力的叠加性可知,空间任一点的电场是周围所有电荷在此贡献电场的矢量和,此即为电场的叠加原理。
点电荷的电场强度
一个点电荷
基于此,由点电荷组成的带电体系的电场就可以根据电场强度的叠加来获得。
离散的点电荷体系的电场为
这是计算电场强度的第一种方法。
电场线及电场通量
电场线:一种描述电场强度矢量分布的模型,它在某处的切线方向对应该点的电场的方向,在某点垂直于电场的单位面积内,穿过的电场线的条数
电场线起始于正电荷或无穷远,终止于负电荷或无穷远。电场线永不相交,不会在没有电荷的地方中断。
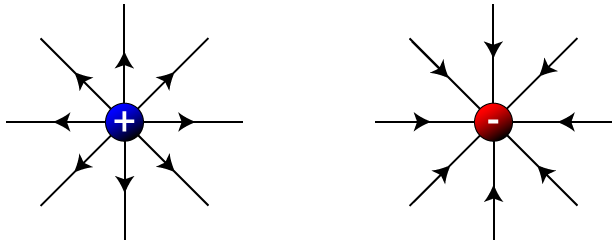
电通量:根据以上电场线的模型易知
规定闭合曲面的法线方向以向外为正,向内为负。因此,若电场线从曲面内射出,则通量为正,否则通量为负。
高斯定理
真空中,穿过任意闭合曲面的电场强度的通量 ,等于该曲面内所包含的电荷的代数和
关于高斯定理要注意:
a. 闭合曲面外的电荷对整个曲面上的电通量没有贡献,曲面上的的电通量全部由内部的电荷贡献。
b. 高斯定理描述的是曲面的通量与内部的电荷之间的关系,并不是描述曲面上的电场与电荷之间的关系。
c. 高斯面上的电场并非只由曲面内的电荷贡献,而是由空间所有电荷共同贡献的。
d. 作为一个数学定理,高斯定理是普遍成立的,对曲面的形状没有任何要求,但是只有当电场分布具有某种对称性时,高斯定理才能为我们所用——用来求空间电场的分布。
当电场分布具有高度对称时,例如球形带电体,圆柱形带电体,无限大带电平面等,电场强度可从积分符号中提出,因而可据此求解电场强度。这是求解电场强度的第二种方法。
典型静电场案例
a. 电荷线密度为
静电场的环路定理
静电场的电场强度沿任意闭合路径的积分必为零,即
电势能与电势
电势能:电荷
电势:单位正电荷在某点的电势能的值,即
电势差:空间两点之间的电势相减得到的就是两点之间的电势差,即
电场力做功:电场力做功等于电荷乘以电势的减少值,即
电势的叠加原理
电场中任一点的电势等于各个点电荷单独存在时对该点形成的电势的代数和,即
点电荷的电势
点电荷
电场强度与电势的关系
电势是电场强度的积分,但是反过来,如何通过电势得到电场强度呢?
电势
等势面:电势相等的点构成的面。一般,电场中相邻等势面的电势差为一常量。这样就导致电场大的地方,等势面较密集,电场小的地方,等势面较稀疏。
等势面与电场线:电场线是从电势高的等势面指向电势低的等势面,等势面与电场线处处正交。
电势为零的点,电场不一定为零,例子:等量异号电荷连线中点。
电场为零的点,电势不一定为零,例子:等量同号电荷连线中点。
导体与电介质的概念
导体是指内部有大量可以自由移动的电荷的物质,最典型的导体是金属,其次是电介质的溶液或熔融态。作为一个特例,石墨是良好的导体。除此之外的绝大多数物质一般没有导电性,称之为电介质。
静电感应
在电场的作用下,导体内的自由电荷发生宏观的定向运动,体内电荷的分布发生重新分布,最终使得导体的两端的表面聚集异号电荷,这种现象称之为静电感应现象。
静电平衡及其条件
定义:在外电场的作用下,导体发生静电感应,当电荷的定向运动已经完全停止时,就表示静电感应已经完成,此时的状态称之为静电平衡。
条件:导体达到静电平衡的条件是,导体内部任何一点的电场强度都为零。
性质:导体达到静电平衡的性质:
a. 导体内部电场强度处处为零,导体表面的电场沿法线方向。
b. 导体内部没有净余电荷,所有的电荷都分布在导体的表面上。
c. 导体的电势处处相等,导体是一个等势体。
导体电荷分布规律
实心导体:电荷只分布在表面上。
空心导体:若空腔内没有带电体,则电荷只分布在外表面上,若空腔内有带电体,则导体内表面将带与该带电体等量异号的电荷量。
导体表面电荷的面密度与对应位置的曲率半径有关,曲率半径越小,则电荷分布密度越大。
根据高斯定理可知,若导体表面电荷密度为
电荷密度随表面曲率增大而增大,而表面附近的电场又与电荷面密度成正比,这导致尖端物体表面附近具有较强的电场,当形成较大的电压时,导致空气电离,形成尖端放电现象。
静电屏蔽
处于静电平衡时,不管导体腔是否接地,腔体外的电场都不对腔体内产生影响;但若要避免腔体内的电场对腔体外的空间产生影响,则导体腔应该接地。
电介质的极化
极化现象:在外电场作用下,介质表面或内部的密度不均匀处会出现电荷集聚,使介质具有宏观极性的现象。
极化电荷:电介质内部的电荷不能自由移动,但由于受到电场的作用,构成电介质的分子在局部发生拉伸或者偏转,导致分子的电矩产生有序排列,最终导致介质表面出现的电荷,极化电荷不能自由移动,也叫束缚电荷。
极化类型:没有偶极矩的分子(无极分子)发生正负电荷分离,形成位移极化;而本身具有电矩的分子(有极分子)则会以转动为主,电矩沿外场规则排列,形成取向极化。
极化强度矢量
极化强度时描述介质极化程度的物理量,定义为介质内单位体积内的电偶极矩的矢量和,先定义平均极化强度如下
极化强度在介质表面沿外法线方向的分量等于曲面上的极化电荷的面密度,即
退极化场
介质的极化电荷在介质内部所产生的电场
退极化场
电位移矢量
电位移矢量
介质中的高斯定理
极化电荷
电容
电容是带电体或者电容器容纳电荷的能力,符号为
孤立导体电容:
常见的几种电容(器)
常见的电容的结果,孤立导体和平行板电容器的结果可作为结论直接使用,其他电容器电容结果不需要当作公式记忆。
孤立导体球:
孤立导体的的电势是相对无穷远点的,如果将导体看作一极,将无穷远点看作另一极,则孤立导体和电容器的电容的定义一致。球形电容器的外球面如果趋于无穷大,那么电容表达式就变成 ,与孤立导体球的电容一致。
电容器的连接
电容器串联的时候,所有的电容器共享一份电荷,但共同分摊全部电压,因此
电容器的能量
三个等价的公式
电场的能量
能量密度公式:
电流与电流密度
电流强度:单位时间穿过导体横截面的电量,即
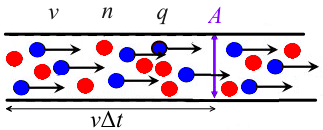
位于面
电流密度矢量:单位时间内,穿过与载流子速度垂直的单位面积的电荷量。采用与上类似的分析方法,得它的表达式为
欧姆定律的微分形式:根据欧姆定律
电源和电动势
非静电力:与静电力的方向相反的某种力
非静电场:单位电荷所受到的非静电力,即
电源:能提供某种非静电力的装置,据此电路中的电流得以持续,它将其他形式的能量转化为电能。
电动势:单位正电荷在电源内部从负极运动到正极的过程中,非静电力所做的呃功,即
磁场与磁感应强度
磁场:奥斯特发现,通电导线周围存在磁场,安培提出分子环流假说,天然磁性与电流的磁场的来源都是运动的电荷。也即,运动电荷激发磁场,以传递彼此之间的相互作用。
磁感应强度:描述磁场的力的性质的矢量,大小为带电粒子受到的最大的磁场力除以电荷与速度的乘积,即
毕奥-萨法尔定律
载流导线中的任意一段电流元
磁矩
一个线圈的面积为
一些特殊通电导体的磁场
无限长载流直导线的磁:方向与电流成右手螺旋关系,大小为
运动电荷的磁场
根据电流的微观表达式
磁场的高斯定理
由于磁感应线是闭合曲线,由闭合曲线对与意闭合曲面的空间关系可知,磁感应线对任意闭合曲面的通量恒为零,即
磁场的安培环路定理
磁感应强度沿任意闭合路径的积分,等于该闭合路径中穿过的电流的代数和乘以
洛伦兹力
洛伦兹力是带电粒子因为在磁场中运动而受到的力,表达式为
根据矢量叉乘的定义,
带电粒子在磁场中的运动
带电粒子虽然有质量,但是重力远比电磁力弱,故忽略重力,粒子的运动分三种情形。
a. 静止或匀速运动
当
b. 匀速圆周运动
当
当
霍尔效应
现象描述:当通电导体置于磁场中时,在垂直于电流和磁场的方向上的两个表面上会出现电势差,这一现象称之为霍尔效应,该电势差成为霍尔电压,用符号
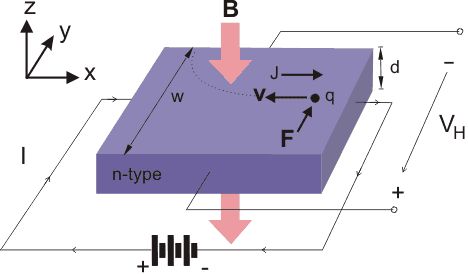
理论解释:载流子受到洛伦兹力作用,会沿与磁场和电流方向都垂直的方向偏转,最终使该方向的两个表面上分别聚集正负电荷,如上图所示。若载流子是电子,则电子定向运动的速度方向朝左,电子受到的洛伦兹力方向朝内侧,导致导体内侧面电势低于外侧面电势。若载流子是正电荷,则载流子也将向内侧表面聚集,导致导体内侧面电势高于外侧面电势。
霍尔电压:当内外两侧之间形成电场时,载流子会受到与洛伦兹力方向相反的电场力,当二者大小相等,即
安培力
安培力即磁场中载流导线所受到的磁场作用力,其微分表达式为
都知道,洛伦兹力不做功,而安培力是洛伦兹力的一种集体作用,本质上也是洛伦兹力,为什么安培力却又能做功呢?可参考本公众号文章“安培力为什么可以做功?”
磁场对载流线圈的作用
a. 磁力
均匀磁场中,任意形状的通电回路所受安培力为
其实这个结论亦可从前面提到的那个推论得到。另外要注意两种曲线积分的差别,如果是微元线段的积分,则结果是曲线总长;但这里是矢量微元的积分,首尾相连构成矢量环的全部矢量之和为零,所以结果是零。
b. 磁力矩
线框的具有大小和形状,它的运动规律应该由力矩决定,通过分析矩形线框的四个边在均匀磁场中的受力,得到其所受力矩为
磁力矩做功
置于均匀磁场中的载流回路,磁力矩对其做功的规律为
磁介质类型
磁介质定义:受到外磁场的作用,能对空间的磁场产生影响的物质,具体讲就是叠加了磁介质的附加磁场,从而使总磁场发生变化。
设外场为
磁介质分类
顺磁质:
抗磁质:
铁磁质:
完全抗磁质:
磁化的形成机理
顺磁性:磁介质的分子内部的电子的轨道磁矩和自旋磁矩之和叫固有磁矩,固有磁矩受外场作用,具有势能,当它的方向与外场同向时,势能最小,因此分子的磁矩会尽量整齐排列,这导致了一个与外场同向的附加磁场。
抗磁性:磁介质分子中的每一个电子的轨道和自旋角动量在外磁场作用下都会产生一个进动,且该进动所对应的磁矩总是与外磁场方向相反,这导致了一个与外场反向的附加磁场。
铁磁性:一些特殊的材料,例如铁、钴、镍及一些合金和氧化物,其内部存在一个个小的自发磁化区,区域内的电子的自旋磁矩同向,称之为磁畴。在外场的作用下,磁畴同向排布产生磁性。
抗磁性是普遍的,但如果磁介质的分子的固有磁矩不为零,则顺磁性远大于抗磁性,因此磁介质表现为顺磁质,否则就是抗磁质。
磁化强度与磁化电流
磁化强度:无论是顺磁质还是抗磁质,磁化后 ,其内部的分子的磁矩之和都不为零,定义磁化强度为
磁化电流:磁介质表面上,由经过表面的分子环流拼接而成的电流,也叫束缚电流。它不是载流子的定向运动导致的,但与载流子的真实电流(自由电流)等效的产生磁场。
磁化强度的安培环路定理:磁介质内部,磁化强度对任意闭合回路的积分等于回路内穿过的磁化电流的代数和,表达式为
磁场强度
定义磁场强度为
磁介质中的安培环路定理
考虑束缚电流
磁介质中的高斯定理
磁介质的附加磁场与真空中的磁场一样,磁感应线都是闭合的,对任意闭合曲面的通量为零,因此高斯定理与真空中的形式一致,即
法拉第电磁感应定律
闭合回路中的磁通量发生变化时,在闭合回路上所产生的感应电动势与磁通量的变化率成正比,符号相反,即
高中所学的楞次定律是一种定性的描述,是能量守恒定律的一种体现,现在通过负号的形式包含在法拉第电磁感应定律中。
动生电动势
由于导体的运动导致磁通量的变化,从而所引起电磁感应现象,所产生的电动势叫动生电动势,包含切割磁力线,回路的形变,回路移动等多种情况,服从法拉第电磁感应定律。
如果是一段导体运动,则计算公式为
如果是线框在磁场中转动,设线框面积为
动生电动势公式的由来:根据电动势的定义,任何电动势必须是某种非静电场将单位正电荷从负极移到正极的过程中所作的功,即 分析发现候选力只有洛伦兹力,因此非静电场为 代入即得到动生电动势的计算公式。
感生电动势
当导体保持不变而磁场变化,导致磁通量变化引起电磁感应,其电动势叫做感生电动势,根据法拉第电磁感应定律,有
自感
闭合回路自身的电流发生变化时,穿过回路的磁通量发生变化而导致在回路中产生感应电动势,这种电磁感应现象叫做自感。
设回路中的磁通量
互感
彼此靠近的通电回路的电流发生变化时,所激发的磁场在穿过对方所形成的磁通量发生变化,导致在彼此回路上形成感应电动势,这种现象叫做互感,所产生的电动势叫互感电动势。
假设两个回路的电流分别为
磁场的能量
考察一个含有自感的电路,若要满足能量守恒定律,线圈的磁场必然储存能量。电源的输出功率大于电阻的发热功率,这个差值就是线圈的磁场的能量,据此得到
位移电流
电荷激发静电场,恒定电流激发恒定磁场,而变化的磁场也会激发一种新的电场,那么变化的电场是否也可以激发磁场呢?实际上这种想法不是纯粹为了满足这种电磁对称性,因为在非稳恒电路中,安培环路定理出现了矛盾。
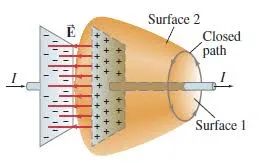
如上图所示,在电容器充放电过程中,导线上是有电流的,只不过不是稳恒电流而已。根据安培环路定理,磁场强度沿图中闭合路径的积分等于任一以该路径为边界的曲面上的电流密度的通量,例如图中所示的两个曲面

天才的麦克斯韦分析发现,无论电容器充电还是放电过程中,极板间的电位移通量和导线上的电流之间总是满足如下关系
注意:这里的等号是定义的含义,而上面两式中的等号只是比较的关系。
位移电流
于是,磁场和电场可以相互激发,为电磁波理论建立了基础。
全电流定律
位移电流激发的磁场与传导电流激发的磁场本身没有任何差别,合在一起就是总的磁场,定义全电流
引入位移电流之后,全电流在任何情况下都是连续的,之前安培环路定理存在的矛盾现在消除了。
电磁场
电场和磁场除了分别由电荷和运动的电荷激发外,彼此还可以相互激发,电场和磁场彼此联系,相互转化,构成电磁场。
电磁场中,带电粒子受力为
麦克斯韦方程组
描述电磁场的普遍规律的四个方程是:
a. 静电场是电荷激发的,但感生电场无源
此7个方程是电磁场最基本的规律。
电磁波的波动方程
平面电磁波的动力学微分方程为
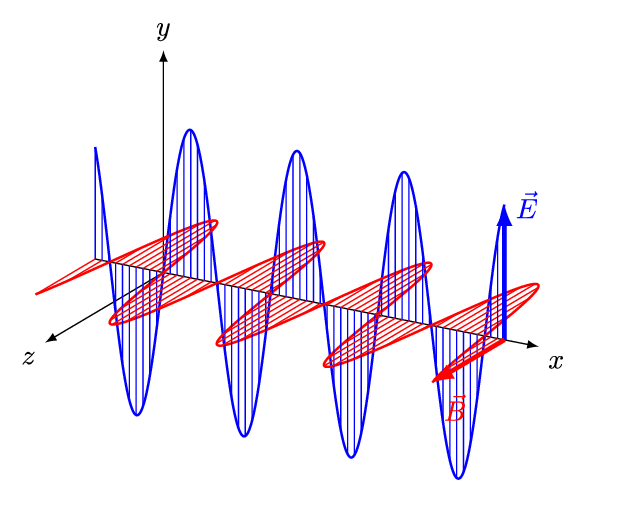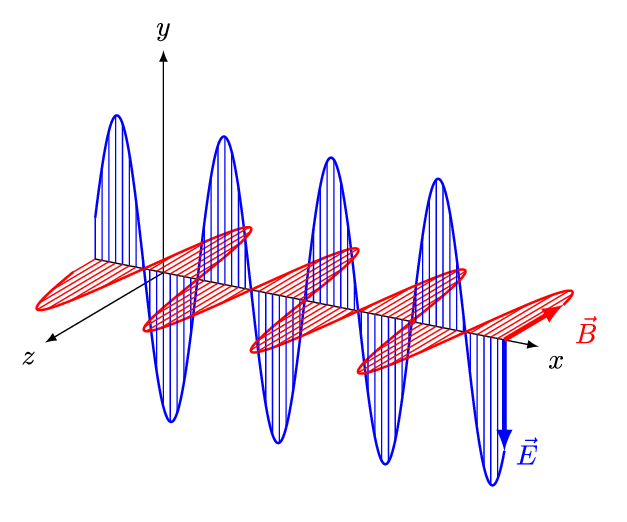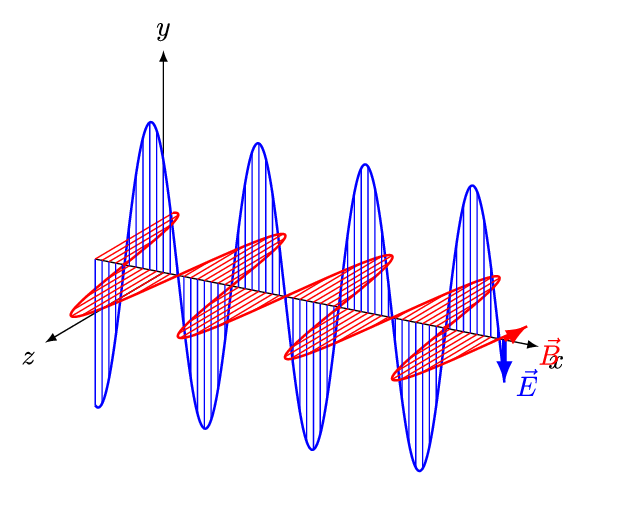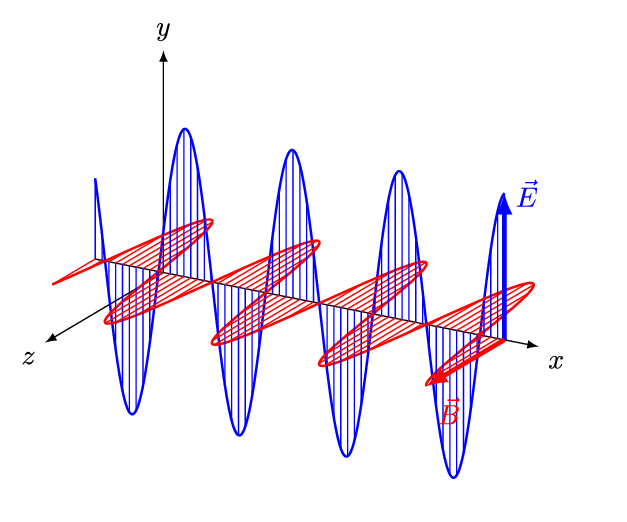
电磁波的性质
a. 电磁波是横波,电场强度和磁场强度与波线垂直,且二者也相互垂直。
b. 电磁波具有偏振性,电场和磁场都在各自的平面内振动。
c. 电场强度和磁场强度保持同相位的关系,瞬时值的关系为
电磁波的能量
波印廷矢量:电磁场的能量密度
- The End -
版权声明:欢迎转发本号原创内容,转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系删除。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/入群/赞助 请加微信:15881101905,备注关键词

“阅读是一种习惯,分享是一种美德,我们是一群专业、有态度的知识传播者
↓↓↓ 戳“阅读原文”,加入“知识星球”,发现更多精彩内容.
分享💬 点赞👍 在看❤️@以“三连”行动支持优质内容!